基于二型模糊逻辑系统的改进卡尔曼滤波算法

华 晶，何火娇，王映龙

（1.江西农业大学 软件学院，江西 南昌330045；2.南昌大学 机电工程学院，江西 南昌330031；3.江西农业大学 江西省高等学校农业信息技术重点实验室，江西 南昌330045）

0 引 言

常用于状态估计的滤波器有中值滤波、均值滤波和卡尔曼滤波等。其中，卡尔曼滤波［1－3］应用最为广泛。卡尔曼滤波算法的性能非常依赖于先验噪声统计特性的质量。已经证明噪声先验统计特性不准确可能严重降低滤波算法的性能［4］，甚至导致滤波发散。事实上，在很多实际应用中，由于各方面的因素，噪声统计特性的估计与实际不符。在使用传统的卡尔曼滤波算法进行状态估计时，若噪声的协方差仍然用先验估计值，必然会使状态估计值产生较大的误差，影响估计的准确度。针对这一问题，国内外学者先后提出了许多自适应滤波方法［5－8］。这些方法的基本思想都是：在卡尔曼滤波过程中，使用自适应技术对噪声统计特性进行实时调整。然而，迄今为止，绝大多数方法都是集中在利用一型模糊逻辑实现自适应调整。本文提出一种二型模糊卡尔曼滤波算法 （简称为IT2FKF），在传统卡尔曼滤波算法中使用二型模糊逻辑系统不断地调整噪声方差矩阵，使其逐渐逼近真实噪声水平，从而避免滤波的发散，并提高滤波精度。并通过仿真实验验证了该算法的有效性和可行性。

1 二型模糊逻辑系统

二型模糊集合［9－15］的概念是由Zadeh教授在普通模糊集合 （一型模糊集合）的基础上提出的。它与一型模糊集合的不同在于，它的隶属度本身存在模糊性，是一个一型模糊集合，从而能更好地描述不确定性。

一个定义在论域X 上的二型模糊集合珦A 可以表示为

其中，μ珦A（x）是x 的隶属度函数，它是 ［0，1］上的一个普通模糊集合；u和fx（u）分别为主、次隶属度值。

如果一个模糊逻辑系统中至少使用一个二型模糊集合，则称之为二型模糊逻辑系统，主要由以下5个部分构成。

1.1 模糊化

当x ＝x′时，μ珦AX（x）＝1／1；

当x ≠x′时，μ珦AX（x）＝1／0。

1.2 模糊规则

若一个二型模糊逻辑系统有p 个输入x1∈X1，…，xp∈Xp，并且包含M 条规则，那么，第l条规则可写为

1.3 模糊推理

基于已设置好的模糊规则，模糊推理把输入的二型模糊集合转换成输出的二型模糊集合。

Rl的次隶属度函数为

由输入与规则合成得到输出珟Bl的隶属函数为

激发集是区间一型集合，表示为

在推理过程中，n 个前件通过 “交”运算连接，而m条模糊规则通过 “并”运算进行组合。

1.4 降 型

由于模糊推理的结果是二型模糊集合，为了进行下一步的解模糊运算，先将二型模糊集合转换成一型模糊集合。此步骤可以看作是解模糊的扩展。

二型模糊系统常用的降型方法有很多，其中，centerof－sets相对于其它方法具有实际意义，所以本文中采用这种降型方法，它的表达式如下

1.5 解模糊

二型模糊逻辑系统的解模糊是将降型得到的一型模糊集合映射为实数输出。式 （7）是一个区间集合，解模糊只需要求区间端点的中心即可

2 改进的自适应卡尔曼滤波

在传统卡尔曼滤波算法中，都是假定事先知道系统的过程噪声和量测噪声的协方差矩阵。在很多实际应用中，过程噪声的统计特性可以通过实验手段获得。但是，量测噪声的统计特性是不确定的。然而，卡尔曼滤波算法估计的准确度和先验噪声统计特性的质量密切相关。因此，为了使系统的量测噪声更接近于实际情况，本文使用二型模糊逻辑实时估计量测噪声方差R，使得新息的理论协方差和实际协方差相匹配，从而影响滤波的增益值，修正状态估计值，提高估计准确度。

新息的理论方差为

新息的实际方差为

其中，ri为新息或残差，i0＝k－M＋1 是估计窗口的第一个采样。M 为采样窗口的长度，一般根据经验选定。

理想情况下，新息的理论方差和实际方差应该大约相同，如果两者值偏差太大，这就表示量测噪声水平发生了改变，那么，这时就应该采取一定的办法调节理论方差，使得它重新接近于实际方差的值。

为了检测两者之间的差异，定义一个新的变量d

由式 （9）和式 （11）可知，增大Rk将导致Sk增大，反之亦然。那么，可以由dk的值来调整Rk，从而改变Sk的值，最终减小Sk与Ck之间的差异。因此，以dk中的对角元素dk（i，i）作为模糊推理系统的输入语言变量，输出语言变量为相应的调节增量因子fk。其调整方法为

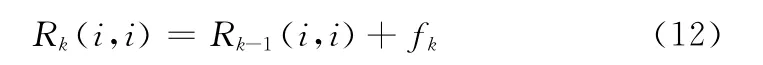
定义输入变量dk的模糊集合为 ｛NL （负大），NS （负小），ZO （零），PS （正小），PL （正大）｝，输出变量fk的模糊集合 为 ｛IL （增 大），IS （增 小），MN （保 持），DS（减小），DL （减大）｝，它们的隶属度函数如图1所示，均采用二型三角隶属函数。

图1 输入／输出变量隶属函数

根据以上分析，模糊推理规则见表1。

表1 模糊推理规则

降型和解模糊方法分别采用文中第一部分介绍的centerof－sets和centroid。将每次模糊推理系统的输出fk带入式（12），对Rk进行自适应调整。IT2FKF算法流程如图2所示。

图2 IT2FKF算法

3 仿真实验

3.1 仿真模型

采用以下线性系统模型［16］进行仿真实验

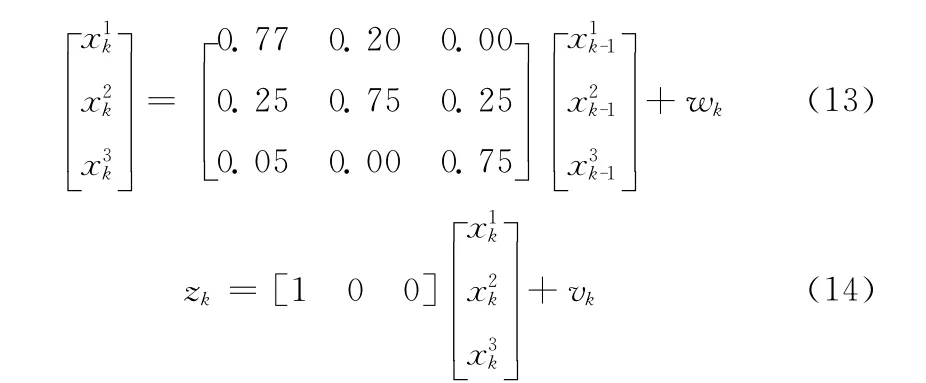
3.2 实验结果及分析

为了验证IT2FKF 算法的有效性，我们将其与传统卡尔曼 滤 波 算 法 （KF）、一 型 模 糊 卡 尔 曼 滤 波 算 法［16］（T1FKF）进行对比。

表2 给出了量测均方误差，以及 KF、T1FKF、IT2FKF算法的估计均方误差的比较。显然，IT2FKF的估计均方误差最小。

表2 量测和估计均方误差对比

图3为状态x1（位置）的跟踪曲线，实线表示位置的实际值，点划曲线表示位置的测量值，长虚线表示用IT2FKF算法对位置的估计。可以看出，尽管事先不知道准确的量测噪声协方差，但是IT2FKF 算法可以得比量测位置更接近于实际位置的估计。

图3 位置跟踪曲线比较

图4为传统卡尔曼滤波算法、一型模糊卡尔曼滤波算法和二型模糊卡尔曼滤波算法进一步的比较。长虚线、点划线和实线分别表示用KF、T1FKF 和IT2FKF 算法得到的位置的估计值与实际值之间的误差。由图4 可知，IT2FKF算法比其它两种算法的估计误差都更小，滤波精度更高。

图4 位置估计误差比较

4 结束语

针对实际情况下，量测噪声协方差不能准确知道或者不断变化这一问题，本文提出了一种基于二型模糊逻辑系统的自适应卡尔曼滤波算法 （IT2FKF）。为了验证本文所提出的IT2FKF算法的性能，采用一个线性系统模型进行仿真实验，并将其与传统卡尔曼滤波、一型模糊卡尔曼滤波两种算法进行对比。仿真实验结果表明，IT2FKF 算法有效地提高了状态估计的准确度。

文中所采用的区间二型模糊集合的隶属函数是根据经验而选择的，需要耗费大量的时间，因此，后期的研究工作将着重解决此问题。

［1］Grewal M S，Andrews A P.Kalman filtering：Theory and practice using MATLAB ［M］.John Wiley ＆Sons，2011.

［2］Simon D.Kalman filtering with state constraints：A survey of linear and nonlinear algorithms ［J］.IET Control Theory ＆Applications，2010，4 （8）：1303－1318.

［3］WANG Taobo，HUANG Baojun.4Dflight trajectory prediction model based on improved Kalman filter ［J］.Journal of Computer Applications，2014，34 （6）：1812－1815 （in Chinese）.［王涛波，黄宝军.基于改进卡尔曼滤波的思维飞行航迹预测模型 ［J］.计算机应用，2014，34 （6）：1812－1815.］

［4］GUO Yingshi，WANG Chang，ZHANG Yaqi.Analysis of noise variance’s effect on Kalman filter result［J］.Computer Engineering and Design，2014，35 （2）：641－645 （in Chinese）. ［郭应时，王畅，张亚岐.噪声方差对卡尔曼滤波结果的影响分析［J］.计算机工程与设计，2014，35 （2）：641－645.］

［5］CHEN Xinglin，LI Peng，SONG Shenmin.The multi sensor information fusion based on fuzzy adaptive Kalman filter［J］.Aerospace Control，2011，29 （1）：19－22 （in Chinese）. ［陈兴林，李鹏，宋申民.基于模糊自适应卡尔曼滤波算法的多传感器信息融合 ［J］.航天控制，2011，29 （1）：19－22.］

［6］Al－Hamadi H M，EL－Naggar K M.Measurement of synchronous machine parameters using Kalman filter based fuzzy logic estimator［J］.Measurement，2010，43 （10）：1327－1335.

［7］Yadaiah N，Srikanth T，RAO VS.Fuzzy Kalman Filter based trajectory estmation ［C］／／Proceedings of the International Conference on Hybrid Intelligent Systems，2011：566－571.

［8］Ibarra－Bonilla MN，Escamilla－Ambrosio PJ，Ramirez－Cortes JM，et al.Pedestrian dead reckoning with attitude estimation using a fuzzy logic tuned adaptive Kalman filter ［C］／／Proceedings of the International Symposium on Circuits and Systems，2013：1－4.

［9］Aisbett J，Rickard J T，Morgenthaler D G.Type－2fuzzy sets as functions on spaces［J］.IEEE Transactions on Fuzzy Systems，2010，18 （4）：841－844.

［10］Khosravi A，Nahavandi S，Creighton D，et al.Interval type－2 fuzzy logic systems for load forecasting：A comparative study［J］.IEEE Transactions on Power Systems，2012，27（3）：1274－1282.

［11］WU D.On the fundamental differences between interval type－2and type－1fuzzy logic controllers ［J］.IEEE Transactions on Fuzzy Systems，2012，20 （5）：832－848.

［12］Wu D，Mendel J M.On the continuity of type－1and interval type－2fuzzy logic systems［J］.IEEE Transactions on Fuzzy Systems，2011，19 （1）：179－192.

［13］Castillo O，Melin P.A review on the design and optimization of interval type－2fuzzy controllers［J］.Applied Soft Computing，2012，12 （4）：1267－1278.

［14］Castillo O，Melin P，Alanis A，et al.Optimization of interval type－2fuzzy logic controllers using evolutionary algorithms［J］.Soft Computing，2011，15 （6）：1145－1160.

［15］Wu D.Approaches for reducing the computational cost of in－terval type－2fuzzy logic systems：Overview and comparisons［J］.IEEE Transactions on Fuzzy Systems，2013，21 （1）：80－99.

［16］Li Jian，Lei Yanhua，Cai Yunze，et al.Multi－sensor data fusion algorithm based on fuzzy adaptive Kalman filter ［C］／／Proceedings of the Chinese Control Conference，2013：4523－4527.