基于改进谱聚类的提升机故障诊断算法

陈少达，夏士雄，王志晓

（中国矿业大学 计算机学院，江苏 徐州221116）

0 引 言

国内外对矿井提升机的故障诊断技术方法［1，2］主要分为3类，分别是基于解析模型、基于信号处理和基于智能技术与知识［3］。谱聚类［4］是这些方法中的一个重要分支，其通过分析一个与故障数据集相关的矩阵的特征向量和特征值来得到故障诊断结果。谱聚类方法具有很多优点，如，仅与数据点的数目有关，而与数据对象的维数无关，可以避免由于特征向量的过高维数所造成的奇异性问题。另外，谱聚类不对数据的全局结构作假设，可以避免“局部最优”的问题［5］。

传统谱聚类存在一些缺陷与不足，比如，需要人为确定聚类数目，对初始聚类中心敏感和鲁棒性较差等。谱聚类采用的节点矩阵主要有两大类，分别是Laplace矩阵和Normal矩阵。在基于Laplace矩阵进行故障诊断时，无法知道故障数据能划分为多少类，需要事先人为设置k 值和初始聚类中心点。Normal矩阵在一定程度上解决了该问题：Normal矩阵是半正定矩阵，存在k－1个与其最大特征值1相近的非平凡特征值 （非平凡特征值是值不为1的特征值），且这k－1个特征值所对应的特征向量的元素呈现阶梯分布，为故障诊断提供了数目依据，阶梯数即为故障种类数t。但是，当提升机故障分类不明显时，Normal矩阵的这k－1个特征向量就不会呈现十分明显的阶梯状，而是接近一条连续曲线［6］，此时无法通过阶梯数目判断该故障种类数k。

数据场模型［7］作为一种描述数据对象间的非接触相互作用的数学模型，能够很好地揭示数据对象的聚类特性。提升机故障数据间并不孤立，而是存在相互的作用与联系。本文将数据场模型引入到谱聚类方法中，利用数据场模型剔除孤立数据点，并借助数据场模型判断谱聚类算法的k值和初始聚类中心点，最后利用K－means聚类算法进行聚类划分。对UCI数据集和提升机轴承故障数据的实验结果表明，将谱聚类与数据场结合能够有效提高提升机故障诊断的性能。

1 数据场模型

场作为物体非接触相互作用所需的介质最早由英国物理学家法拉第在电磁学研究中提出。场可以描述物体在空间中的分布状况，通过量化物体间的空间分布和变化规律，得到物体间的作用关系。同样在数据挖掘研究中，大量的数据之间存在着非直接的联系，可以通过将数据抽象成数域空间，从而建立关于数据的场，应用物理学中场理论和研究方法，对场中的数据进行科学分析与研究，这种建立起来的关于数据的场就叫做数据场［8］。大量的数据场的研究与实验结果表明数据场理论在处理数据之间的相互联系上有着非常好的效果，目前数据场被应用于大量的数据挖掘学科研究中，比如人脸识别［9］、层次聚类、传感器网络路由［10］等领域。

提升机故障数据间并不孤立，而是存在相互的作用与联系。数据场模型作为一种描述数据对象间的非接触相互作用的数学模型，能够很好地揭示提升机故障数据对象间的聚类特性。因此，本文将数据场模型引入到提升机故障数据中，利用数据场模型刻画故障数据间的相互作用与联系。可以从势、梯度和场强等多个角度描述数据场。

定义 已知空间Ω 中包含数据集D ＝｛x1，x2，…，xn｝及其产生的数据场，其中n为数据集D 的个数，令数据对象的位置矢量为x1，x2，…，xn，则任一场点x点处的势值可表示为

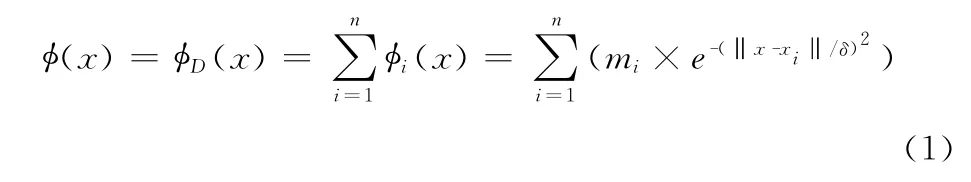
影响因子对于任一场点的势值有着直接的影响。在式（1）中若δ值很小时，那么e的指数就会非常的小，从而每一个点的势值都会很小，得到的势值和就会很小。反之，若δ值很大，那么e的指数就会相对较大，得到的势值也会较大。因此，需要选择合适的影响因子δ，使数据场的势值分布真正体现语义的内在分布。影响因子优选势熵法［11］。

2 基于改进谱聚类的提升机故障诊断

针对谱聚类算法存在的问题与不足，本文将数据场模型引入到谱聚类方法中，利用数据场模型剔除孤立数据点，并借助数据场模型判断谱聚类算法的k 值和初始聚类中心点，最后利用K－means聚类算法进行聚类划分。

2.1 孤立点检测

孤立点指数据集中与其它数据对象有较大不同的对象，或是那些显著偏离其它数据的对象。本文给定一个阈值（经过多次实验得出），孤立点可定义为在给定阈值范围内势值最小的数据点。孤立点检测的具体过程就是计算每个数据点的势，并选择最小势的数据点，如果该数据点满足孤立点条件，将其作为一个孤立点，标记剔除。具体算法如下：

输入：数据集Xm＝（x1，x2，…，xm）

输出：孤立点集合

步骤：

（1）依据数据集Xm＝（x1，x2，…，xm）构建数据场；

（2）根据式 （1）计算数据场内各点势值；

（3）找出势值最小的数据点，将它从数据集Xm＝（x1，x2，…，xm）中剔除，存入孤立点集合；

（4）重复上述步骤直至找出所有孤立点。

2.2 聚类数目及初始聚类中心确定

数据场能够合理、客观地展示数据对象间相互影响和相互作用，势值是空间中所有数据对象作用力的叠加，全面体现了数据对象在整个数据空间的重要程度，其势心更好地表达了数据对象的重心位置，通常称势心为 “准数据中心”。通过计算出故障数据的势心，即可得出聚类个数k及初始聚类中心，从而自动确定了聚类分组数。在剔除孤立点之后，在剩下的数据集中确定聚类个数k 及初始聚类中心，其算法流程如下：

输入：剔除孤立点后的数据集Xn＝（x1，x2，…，xn）

输出：聚类个数k及初始聚类中心集合

步骤：

（1）依据数据集Xn＝（x1，x2，…，xn）构建数据场；

（2）根据式 （1）计算出每个数据对象的势值，存入势值矩阵F；

（3）利用Hesse矩阵的特征值确定局部极大值，确定聚类个数k及初始聚类中心。

2.3 故障诊断

基于改进谱聚类的提升机故障诊断算法主要步骤如下：

（1）对 数 据 集Xn＝（x1，x2，…，xn）构 建 相 似 度 矩 阵W ∈Rn×n，其中Wij＝exp（－d（xi，xj／2δ2）），i≠j；

（2）构造Laplacian矩阵L＝D－1／2WD－1／2，其中Dij＝Wij，D 为对角矩阵；

（3）根据2.2节给定的算法计算出聚类数目k 及初始聚类中心集合C ＝（c1，c2，…，ck）；

（4）分别计算出Laplacian 矩阵L 的特征值和特征向量，选取特征值中最大的k个值对应的特征向量z1，z2，…，zn，构造矩阵Z ＝［z1，z2，…，zk］∈Rn×k；

（6）将矩阵Y 中的每一行视为Rn×k中的一个样本，使用步骤 （3）得出的初始聚类中心集合C＝（c1，c2，…，ck）赋予K－means算法的初始聚类，然后对其进行聚类，将其划分为k类；

（7）将初始样本点xi划分为第j 类，当且仅当矩阵Y的第i行被划分到聚类j 中。

3 仿真实验

为验证改进算法的有效性，本文选取UCI数据和提升机轴承故障数据进行测试。本文利用上述数据集对比了3种算法的性能，这3种算法分别是：经典的K－means算法、传统谱聚类算法 （NJW）和本文提出的改进谱聚类算法（NJW－Fields）进行测试比较。本文实验环境为：处理器2.94GHz，内存3GB，硬盘320GB，操作系统Windows 7，编译环境为matlab7.0，所得出的实验结果为每个算法运行30次取得的平均值。本文以F－measure作为评价指标。

3.1 UCI数据集

Iris数据集可划分为3个类，每类50个数据，每个类别代表一种类型鸢尾花，150 个样本在3 个类簇中分布均匀。Wine数据集具有良好的聚类结构，包含178 个样本，13个数值型特征，可聚为3 个类，每一类样本数量不同。Zoo数据集共有101个样本数据，可划分为7类。

图1为3种算法在Iris数据集上的每个聚类结果的Fscore曲线图，可以看出在Iris数据集上，传统NJW 算法在第二类聚类结果比K－means算法好，但是其第三类聚类结果比K－means算法稍差，然而本文提出的NJW－Fields算法在3个聚类结果都好于或等于其它两个算法的聚类结果。

图1 Iris数据集聚类F－score值

图2为3种算法在Wine数据集上的每个聚类结果的F－score曲线图，可以看出在Iris数据集上，传统NJW 算法每一个聚类结果均比K－means算法结果好，本文提出的算法的聚类结果好于传统NJW 算法聚类结果，说明本文提出的NJW－Fields算法在具有良好聚类结构的数据集上聚类结果的效果明显。

图2 Wine数据集聚类F－score值

图3为3种算法在Zoo数据集上的每个聚类结果的Fscore曲线图。可以看出，由于Zoo数据集元素线性不可分的关系，K－means算法聚类结果在第3 类和第7 类聚类结果效果都比较差，NJW 算法也在第3 类聚类结果表现较差，两种算法在其它聚类上的效果也不明显。相反，本文提出的NJW－Fields算法在各类别的聚类效果较为均匀，总体聚类结果的效果也较为明显。

图3 Zoo数据集聚类F－score值

表1为K－means算法、NJW 算法和本文提出的NJWFields算法的MacroF1 值，可以看出本文的算法由于事先为最终的聚类算法自动指定了k 值和k 个聚类中心，在3种数据集上的聚类结果都好于其它两种算法的聚类结果。

表2为K－means算法、NJW 算法和本文提出的NJWFields算法在多次运行过程中，取得的平均运行时间的比较，可以看出在聚类过程中K－means算法消耗的时间最多，而NJW 算法由于构建了Laplace矩阵，并且取前k 个向量作为聚类数据集，从而加快了算法的运行速度，其运行时间较短。本文的NJW－Fields算法由于事先将初始聚类中心点给予了聚类算法，使得本算法在运行时间大大缩短，明显快于前两种算法的程序运行时间。

表1 3种算法在3种数据集MacroF1比较

表2 3种算法在3种数据集上运行的时间比较

3.2 提升机轴承故障数据集

本文搜集了部分提升机轴承故障样本，样本数据经过一定预处理，选取其中的典型数据建立故障样本数据集。每类故障有1630个样本数据，每个样本数据含10个信号特征，共有5类故障。部分故障数据见表3。

将提升机故障信号数据分别导入K－means算法、NJW算法、NJW－Fields算法所实现的程序中，得出3种算法的运行时间和MacroF1值对比表格，见表4、表5。

表4 3种算法运行时间对比

表5 3种算法MacroF1值对比

表4为提升机轴承故障数据集分别在K－means算法、NJW 算法、NJW－Fields算法程序上运行统计的时间，可以看出，K－means 算法速度最慢，NJW 算法其次，本文NJW－Fields算法在3种算法中运行时间最短。

表5为提升机轴承故障数据集分别在K－means算法、NJW 算法、NJW－Fields算法得出的F－measure综合值，可以看出，K－means算法得分最低，为0.5728，NJW 算法其次，得分为0.6183，本文NJW－Fields算法在3种算法中得分最高，为0.6571，根据F－measure得分越高，算法的效果越好的特性，可得出本文提出的NJW－Fields算法较其它两种算法效果都较好。

4 结束语

矿井提升机一旦发生故障，便会造成巨大的人力和财力损失。矿井提升机故障诊断对煤矿安全生产至关重要。提升机故障诊断方法有很多，谱聚类是一种典型方法。传统谱聚类需要人为地确定聚类数目，对初始聚类中心敏感，且鲁棒性较差。

本文将数据场模型引入到谱聚类方法中，借助数据场模型的优点改善谱聚类算法存在的缺陷与不足，提高故障诊断的性能。改进的谱聚类算法利用数据场模型剔除孤立数据点，并借助数据场模型判断谱聚类算法的k 值和初始聚类中心点，最后利用K－means聚类算法进行聚类划分。对UCI数据集和提升机轴承故障数据的实验结果表明，将谱聚类与数据场结合能够有效提高提升机故障诊断的性能。

［1］WANG Zhiping.Fault diagnosis and repair technology of coal mining machinery and equipment［J］.Coal Technology，2013，32（8）：246－247（in Chinese）.［王智萍.煤矿机械设备的故障诊断及维修技术探析［J］.煤炭技术，2013，32 （8）：246－247.］

［2］ZHOU Decai，XIA Shixiong，WANG Zhixiao.Improved fault diagnosis based on the mean C ［J］.Microelectronics ＆ Computer，2012，29 （11）：120－122 （in Chinese）. ［周德财，夏士雄，王志晓.基于改进C均值的故障诊断 ［J］.微电子学与计算机，2012，29 （11）：120－122］.

［3］NIU Qiang.Fault diagnosis of mine hoist semantic environment［D］.Xuzhou：China University of Mining，2010 （in Chinese）.［牛强.语义环境下的矿井提升机故障诊断研究 ［D］.徐州：中国矿业大学，2010］.

［4］ZHANG Yan，TANG Baoping，DENG Lei.Mechanical fault diagnosis spectral clustering initialization based NMF ［J］.Journal of Scientific Instrument，2013，34 （12）：2806－2811（in Chinese）.［张炎，汤宝平，邓蕾.基于谱聚类初始化非负矩阵分解的机械故障诊断 ［J］.仪器仪表学报，2013，34（12）：2806－2811.］

［5］WANG Na，DU Haifeng，ZHUANG Jian，et al.For troubleshooting network segmentation spectral clustering method ［J］.Mechanical Engineering，2008，44 （10）：228－233 （in Chinese）.［王娜，杜海峰，庄健，等.用于故障诊断的网络分割谱聚类方法 ［J］.机械工程学报，2008，44 （10）：228－233］.

［6］FU Chuanyi，XING Jieqing，CHEN Huandong.Spectral clustering and its research progress ［C］／／Seventh International Conference on Computational Intelligence and Security，2011.

［7］GAN Wenyan，HE Nan，LI Deyi，et al.Based topology discovery potential of online communities ［J］.Journal of Software，2009，20 （8）：258－262 （in Chinese）.［淦文燕，赫南，李德毅，等.一种基于拓扑势的网络社区发现方法 ［J］.软件学报，2009，20 （8）：258－262.］

［8］LI Deyi.The era of artificial intelligence research and development network ［J］.Intelligent Systems，2009，4 （1）：1－6（in Chinese）.［李德毅.网络时代人工智能研究与发展 ［J］.智能系统学报，2009，4 （1）：1－6.］

［9］WANG Shuliang，ZOU Shanshan.Face recognition method utilizing expression data field［J］.Wuhan University（Information Science Edition），2010，35 （6）：738－742 （in Chinese）. ［王树良，邹珊珊.利用数据场的表情脸识别方法 ［J］.武汉大学学报（信息科学版），2010，35 （6）：738－742.］

［10］GUO Liang，ZHU Yi’an，CHI Wenming.Wireless sensor network routing hops protocol based on data field ［J］.Intelligent Instrumentation and Sensors，2010，18 （5）：1214－1216（in Chinese）.［郭亮，朱怡安，迟文明.基于跳数数据场的无线传感器网络路由协议研究 ［J］.智能仪表与传感器，2010，18 （5）：1214－1216.］

［11］LI Deyi.Uncertainty artificial intelligence［M］.Beijing：Defense Industry Press，2005 （in Chinese）. ［李德毅.不确定性人工智能 ［M］.北京：国防工业出版社，2005］.