基于有限资源的微小型多机器人协同避障策略

李 月，高峻峣，赵靖超，刘 轶

（北京理工大学 机电学院，北京100081）

0 引 言

相对位置测量是机器人编队与环境探测的实现基础，但目前常用的相对定位方法需要机器人拥有昂贵的传感器、大存储容量与高计算能力，如利用激光雷达、摄像头等［3，4］，因此并不适用于低成本、低功耗的微小型机器人。全球定位系统 （GPS）［5］相对于微小型机器人误差较大，在有遮挡或室内环境下无法获得位置信息。有些研究利用超声环进行相对位置估计［6］，但机器人体积限制了可固定声呐的个数，从而会产生较大定位误差，传播较慢的超声信号还会降低实时定位速度。面向资源有限的微小型多机器人系统，设计了一种基于价格低廉、质量较轻的红外测距传感器与微型舵机的局部测量系统，利用扩展卡尔曼滤波技术，融合机器人运动补偿，在线快速测量与估计相邻机器人或障碍物的相对距离与角度。针对非结构化环境，采用 “领航者－跟随者”的编队结构［7］，根据领航者实时探测到的局部环境信息，多机器人进行队形保持与灵活的队形变换，从而保证机器人群作为整体顺利通过障碍区域。

1 相对定位系统设计

式中：ds——红外传感器探测面距离旋转中心的距离。

图1 局部测量系统的硬件实现

令一台机器人为总领航者，其余机器人分别跟踪邻近机器人轨迹并保持一定位置关系，组成 “分领航者－跟随者”编队结构。局部感知系统具有两种工作模式：①障碍物探测模式：如图2 （a）所示，总领航机器人负责环境探测与导航，舵机的旋转角度从0°到90°，两个传感器同时工作，形成相对于机器人航向－90°到90°的探测范围；②位置估计模式：跟随机器人的轨迹跟踪需要实时获取邻近机器人的相对距离与角度，为减少对机器人的识别与相对定位时间，对舵机角度范围α 采用自调节控制，如图2 （b）所示，仅激活一个红外传感器的探测功能，通过控制舵机轴旋转不断测量与领航机器人的距离，同时存储距离值dk与舵机角度值γk，如果在设定的时间阈值TD内探测不到机器人边缘，舵机轴反方向旋转，开始新的测量周期。根据机器人典型的外形形状，可利用局部感知系统对外界环境中的机器人进行有效区分与识别，机器人相对位置的估计方法具体见第3部分。

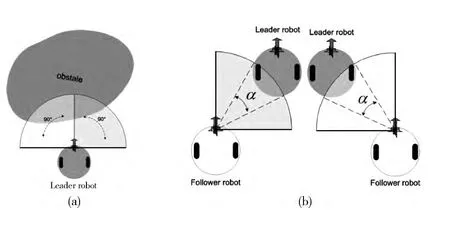
图2 传感系统的两种操作模式

2 协同避障运动规划

本文主要研究基于局部感知的多机器人协同避障，而领航机器人的路径导航不是主要研究内容，仅考虑领航机器人对环境的探测与跟随机器人的协同编队行为，并做出如下假设：①遇到障碍物前机器人队形已形成；②领航机器人与跟随机器人间的距离不超过红外传感器所能探测到的范围；③一个采样周期中机器人的线速度与角速度恒定不变。

由于通信约束与较弱的感知能力，微小型多机器人在避障时需要保持一定的队形与网络连通性。考虑由n 个机器人组成的多机器人系统，rL为总领航机器人，为防止其它机器人rFi（i＝1，2，…，n－1）对rL与环境的识别混淆，rL负责障碍物的探测，而rFi实时跟踪各自被分配的领航者的轨迹。多机器人队形的协同变换主要取决于队形尺寸和障碍物相对位置，以图3的多机器人系统为例，探测到障碍物前机器人呈三角队形，rL的探测范围为xL∈［0，xm＋dL］，yL∈［－dL，dL］，dL是传感器测量极值，机器人半径为Rr，rF1与rF2相对于rL的距离和角度分别为（l1，α1）T和（l2，α2）T。为避免碰撞，机器人间或机器人与障碍物间的最小距离不可超过设定的安全阈值Ds。

图3 扫描范围的区域划分

若在180°范围内检测到障碍物，由两个传感器测得的障 碍 点 坐 标 分 别 被 存 为（，），k ＝1，2，…，p 与（，），k＝1，2，…，q。取点集｛｝与｛｝中距离XL轴最近的点与，即满足＝min｛｝与，点与之间沿YL轴的距离定义为。结合队形尺寸，将rL的探测范围分为5个区域，划分规则见表1，进而得到如下协同避障规则：

（1）如果障碍点在区域I，rL规划路径躲避障碍物，如图4 （a）所示。

表1 扫描区域划分原则

图4 协同避障运动模式

3 相对定位算法

3.1 运动补偿

由于机器人的运动会影响传感器的测量准确性，所以要对所测量点进行坐标补偿。如图5所示，从t＝t1至t＝tm的测量周期内，rF探测到rL的一系列点PFk（k＝1，2，…，m），通过存储的距离与角度值（dk，γk），由式 （1）～式（2）得到相对于Xrk－Yrk坐标系下的坐标值（x）。rL从t＝tk到t＝tm走过的距离为＝vL（m－k）Δt。设在t＝tm，被测点移动到新的位置），则点相对Xrk－Yrk坐标系的位置坐标为

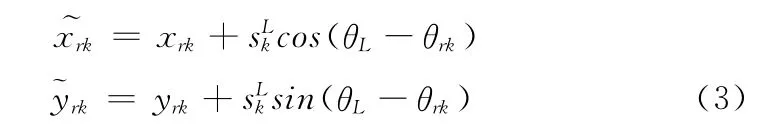
图5 相对运动的坐标补偿

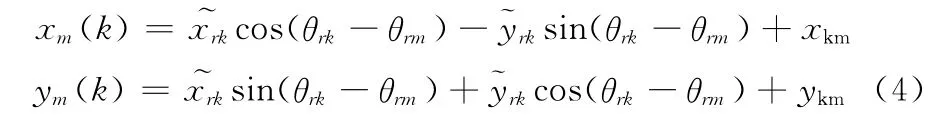
式中：（xkm，ykm）为Xrk－Yrk坐标系原点相对于Xrm－Yrm坐标系的位置坐标

3.2 相对位置估计

根 据所获取的rL系 列 边 缘 点 进 行 对rL位 置（）T的估计计算，先利用马氏距离方法去除噪声点，得到一系列坐标值｛（xm（k），ym（k））｝。设这些点位于圆上

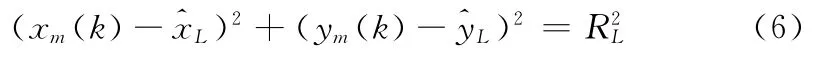
展开得

式中：η（k）为状态变量［C1，C2，C3］T，C1＝－，C2＝－，C3＝＾＋－，y（k）为 理 想 测 量 值［xm（k），ym（k）］T。下面 采 用 扩 展 卡 尔 曼 滤 波 （EKF）算 法［8，9］求t＝tm时刻rL中心在局部坐标系Xrm－Yrm下的坐标。为了得到标 准 形 式 的 测 量 方 程，对f（η（k），y（k））关 于 （（k），（k））展开，其中（k）是η（k）的一阶估计，）是实际测量值

根据

给定状态变量的初始值为η（0），误差协方差矩阵的初始值为P（0），（0）＝E［η（0）］，P（0）＝E［η（0）ηT（0）］状态变量和误差协方差的预测值如下

卡尔曼增益矩阵、状态估计与状态误差协方差矩阵的更新形式如下

为令rF按期望的几何位置关系跟踪rL轨迹，基于建立如图6的rF位置误差模型，rFd为rF下个时刻的期望位置，θL与θF分别为rL与rF的方向角度，给定的相对距离与角度分别为ld和αd。设rF的位置误差［xe，ye，θe］T为

式中：β＝π＋θF－θL－αd。根据rL的控制输入［vL，ωL］T，求出rF期望位置的线速度与角速度

式中：χ＝θL＋αd－π，＝ωL。本文借鉴基于反步法的机器人轨迹跟踪控制器，令rF的位置误差收敛到0［10］

式中：kx与kθ为正常数，且满足：当θe→0 时s→1成立。

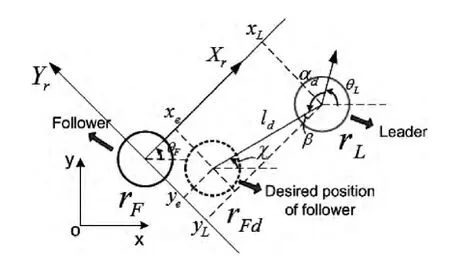
图6 机器人位置误差模型

4 实验结果与分析

为了验证基于相对测量系统的多机器人编队控制的有效性，构建了室内环境下微小型多机器人实验系统，如图7所示，该实验系统由3台微小型移动机器人、顶部摄像头与静态障碍物构成。机器人平台为Φ200mm×100mm 的两轮差分机器人，每台机器人均安装了相对定位系统，载有ARM9嵌入式控制平台进行信息处理与运动控制，通过Zigbee无线通信模块 （CC2530）与PC 机通信。领航机器人rL与跟随机器人rF1、rF2的初始位置分别为 （500mm，0mm，0°），（0mm，500mm，0°）与 （0mm，－500mm，0°），rL控制输入为vL＝0.06m／s，ωL＝0rad／s。两个障碍物尺寸分别为350mm×450mm 和200mm×300mm，障碍物的尺寸与位置对于机器人来讲均为未知。通过PC 机Visual Studio 2008对顶部CCD 摄像头 （640×480）进行图像处理，实时测量与存储机器人的实际位置，为基于相对定位系统的位置估计提供比较标准。

图7 实验系统

图8为机器人的实际运动轨迹。初始阶段rF1与rF2保持三角队形对rL进行跟踪。t＝2s，第一个障碍物出现在rL的扫描范围内，rf1与rf2将测得的距离与角度值（l1，α1）T与（l2，α2）T发送给rL，rL进行队形变换判断，通过减少rf1与rL之间的横向距离避免与障碍物的碰撞；t＝20s，第二个障碍物被测到，通过减少rf2相对rL的横向距离，从而得到无碰撞的光滑路径。图9，图10 中虚线所示的是rf1与rf2利用相对定位系统分别得到的rL在x轴与y轴的相对坐标值。通过对比顶部摄像头测得的实际相对位置 （黑色实线），可以看出该相对定位系统及估计算法在实际机器人编队与避障应用中效果较好，可满足应用要求，同时微小型多机器人系统通过保持一定编队形式的协同运动，顺利驶出障碍区域。

图8 多机器人运动轨迹

图9 领航机器人相对于跟随机器人1实际的与被估计的相对坐标

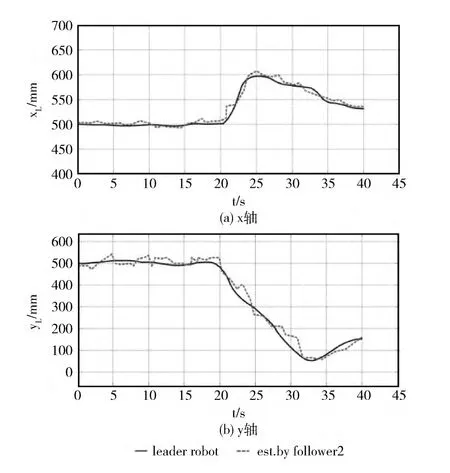
图10 领航机器人相对于跟随机器人2实际的与被估计的相对坐标

5 结束语

本文提出了一种基于红外测距传感器的相对定位系统，用于机器人对邻近机器人相对位置的估计与周围环境的探测。同时，利用该相对定位方法，通过灵活调整机器人间的相对距离和角度，实现了适用于微小型多机器人在静态障碍物环境中的协同运动，有效避免与外部环境的碰撞。真实环境下的实验结果验证了所提途径的有效性与可靠性。下一步的研究工作将会考虑在更加复杂环境中多机器人的运动规划与协同方法。

［1］Mehrjerdi Hasan，Ghomman Jawhar，Saad Maarouf.Nonlinear coordination control for a group of mobile robots using a virtual structure［J］.Mechatronics，2011，21 （7）：1147－1155.

［2］Han Jinlu，Xu Yaojin，Di Long，et al.Low－cost multi－UAV technologies for contour mapping of nuclear radiation field ［J］.Journal of Intelligent and Robotic Systems，2013，70 （1－4）：401－410.

［3］Juan Marcos Toibero，Flavio Roberti，Ricardo Carelli，et al.Switching control approach for stable navigation of mobile robots in unknown environments ［J］.Robotics and Computer－Integrated Manufacturing，2011，27 （3）：558－568.

［4］Filippo Arrichiello，Stefano Chiaverini，Vaibhav Kumar Mehta.Experiments of obstacles and collision avoidance with a distributed multi－robot system ［C］／／IEEE International Conference on Information and Automation，2012：727－732.

［5］Akkaya Ramazan，Omer Aydogdu，Suleyman Canan.An ANN based NARX GPS／DR system for mobile robot positioning and obstacle avoidance ［J］.Journal of Automation and Control，2013，1 （1）：6－13.

［6］Atsushi Fujimori，Hiroshi Kubota，Naoya Shibata，et al.Leader－follower formation control with obstacle avoidance using sonar－equipped mobile robots ［J］.Proceedings of the Institution of Mechanical Engineers，Part I：Journal of Systems and Control Engineering，2014，228 （5）：303－315.

［7］Xu Lingyi，Cao Zhiqiang，Zhao Peng，et al.The identifierbased relative position estimation for leader－follower robotic system ［C］／／IEEE International Conference on Mechatronics and Automation，2014：1691－1695.

［8］Rusdinar Angga，Kim Jungmin，Lee Junha，et al.Implementation of real－time positioning system using extended Kalman filter and artificial landmark on ceiling ［J］.Journal of Mechanical Science and Technology，2012，26 （3）：949－958.

［9］Wei Zhuo，Yang Simon X.Neural network based extended Kalman filter for localization of mobile robots［C］／／World Congress on Intelligent Control and Automation，2011：937－942.

［10］Jan Chen，Sun Dong.Resource constrained multirobot task allocation based on leader–follower coalition methodology［J］.The International Journal of Robotics Research，2011，30 （12）：1423－1434.