鸡蛋清洗喷雾系统中喷嘴的模拟优化
2015-12-20陈永刚阎秋生东莞职业技术学院广东东莞53808广东工业大学广东广州510006
陈永刚 阎秋生(1.东莞职业技术学院,广东 东莞 53808;.广东工业大学,广东 广州 510006)
鸡蛋营养丰富,适于微生物生长,极易受到沙门氏菌等致病菌的污染,未经清洗的蛋壳表面常含有大量的细菌。在发达国家,诸如美国和加拿大等,提倡通过洗蛋来降低鸡蛋表面的细菌总量[1]。在中国,鸡蛋的清洗也逐渐受到人们的重视,自动化的清洗设备广泛地应用于养鸡场和蛋类企业。
在清洗喷水装置(图1)的设计中,喷嘴的排列间距过密则喷水流量需要相应控制,否则会造成水资源的浪费,而控制流量则造成喷头材料使用效率低下,也影响结构美观;而从单纯流体输运的角度,过多的喷嘴还会造成主管道上的压力降过大,距水源远端的喷头喷洒效果不理想,因此喷洒装置的优化设计在这一环节就显得尤为重要。本研究对水气混合的两相流使用VOF模型,同时对离散相,即液滴的雾化过程采用TAB模型,利用Fluent软件实现了对鸡蛋清洗系统喷水装置喷水过程的模拟,并对喷头位置的放置进行了优化。
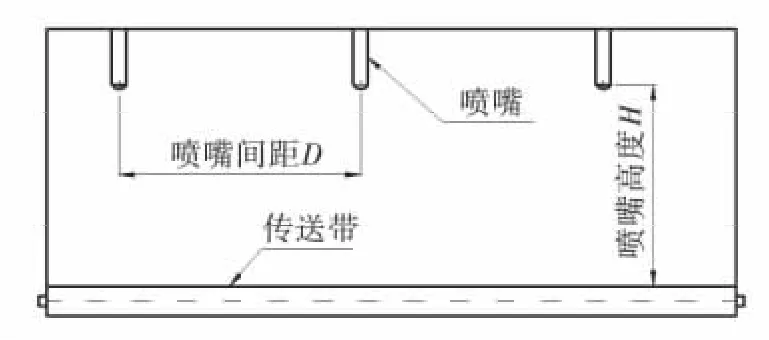
图1 蛋壳清洗系统结构示意图Figure 1 Structure of eggs cleaning system
1 喷嘴的几何结构
所研究喷嘴的几何结构如图2所示,水气混合流体从左边进入,压力水在喷嘴内螺旋运动,与壁面相互作用产生横向速度,然后在喷嘴前汇集,从右端喷出。由于管道的截面半径由大变小,在流量恒定的情况下,将加快流速。空气与水流因密度和压力不同而产生速度差,两相相对作用使得离散相的小水滴不断破碎而完成雾化过程[2]。

图2 喷嘴的几何结构简图Figure 2 Geometry construction of sprayer
2 数值模拟过程
2.1 控制方程
水与空气混合的流体同样遵循流体力学的一般规律,可以根据合理的假设构建相应的控制方程,由于混合流体的可压缩性不能被忽略,有:① 质量守恒方程,② 动量守恒方程。

其中:

牛顿流体的本构方程:

式中:
ρ——混合流体的密度,kg/m3;
t——时间,s;
∇——梯度算子;
u——速度矢量,m/s;
p——压力,Pa;
t——应力张量,Pa;
S——源项;
D——应变速率张量,s-1;
μ——动力黏度,Pa·s。
对于两相流模拟,还需要选择适当的多相流模型。Fluent提供了VOF(volume of fluid)模型,混合物模型和欧拉模型。本研究中,对混合流体喷嘴喷射的模拟采用静态网格,不考虑空气和水之间的溶解性,可采用VOF模型[3],则有:

体积分数连续方程:
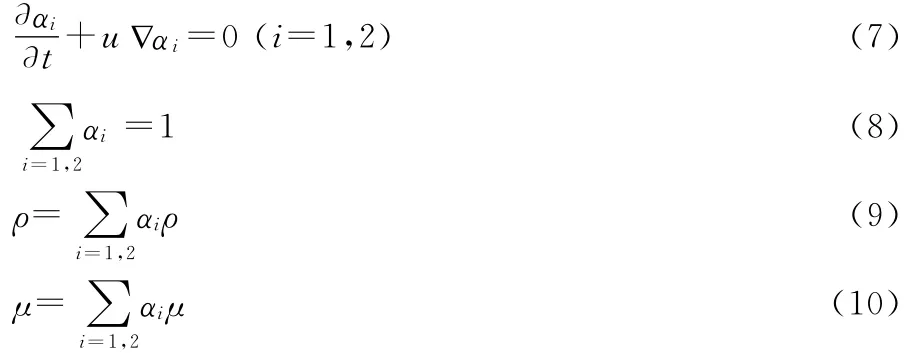
湍动能和耗散率方程:


这两个方程表达的是湍流k—ε模型的k、ε的输运方程,σk、σε是湍动能和耗散率的普朗克常数,二者将k、ε的扩散联系到涡粘性系数μt,表达式见(13):

式中:
g——重力加速度,N/kg;
k——湍流动能,m2/s2;
ε——耗散率;
αi——体积分数;
ρi——混合流体各组分密度[4],kg/m3;
C1ε,C2ε,Cμ——无量纲常数;
σk——湍动能的普朗克常数;
σε——耗散率的普朗克常数;
μt——涡粘性系数,m2/s。
标准k—ε模型方程中包含的5个参数来自综合数据和大量的湍流拟合常数:Cμ=0.09,σk=1.00,σε=1.30,C1ε=1.44,C2ε=1.92[5,6]。
2.2 离散相模型
对于两相流的模拟主要是为了得到喷水效果,即离散相的喷洒情况,为了使模拟结果能够更好地符合实际流场,在模拟过程中考虑了喷嘴出口处初始雾滴的粒径和速度,采用了TAB模型。

式中:
Fa——气动力,N;
Fσ——表面张力,N;
Fμ——粘性力,N;
σ——水滴的表面张力,N/m;
CF、Ck、Cd——无量纲参数,其值根据试验数据和理论拟合通常分别取1/3,8和5;
μ2——水滴动力黏度,kg/(m·s);
y——变形率;
x——初始液滴赤道处半径的变形量,m;
Cb——常数,取0.5;
r——初始的水滴半径,m。
当y=1,即x=0.5r时,认为液滴已经破碎[7,8]。
2.3 网格划分与边界条件
由于喷嘴为圆形,可假设整个流场为轴对称,因此选择轴向任一截面上的1/2作为研究对象。使用ICEM构建几何模型,并对喷嘴内部距出口30mm区域及喷嘴外部300×200的矩形计算区域采用四边形网格离散。由于喷嘴内部,靠近喷嘴出口处发生尺寸的变化,而在喷嘴外部液体喷洒区域主要集中在中轴线附近,所以在保证不发生网格畸变的前提下对喷嘴出口及轴线附近进行网格加密。网格划分结果见图3、4。
对网格划分结果进行检查,得到 Minimum Orthogonal quality为0.933 276。该数值越接近1网格质量越高,证明通过适当的加密,计算区域划分的网格质量已经符合要求。

图3 四边形网格离散结果Figure 3 Quadrangular meshes of computational domain
3 模拟结果
由于蛋壳清洗系统内的混合流体可以选择多种流速,在喷嘴结构不变的情况下,为了得到实际流速与水流喷洒效果的关系,从而确定喷嘴安放间距和安放高度,混合流体的初始速度选择15mm/s和150mm/s两种。假设流场为稳态流场,采用压力修正算法求解标量控制方程,由于喷嘴竖直放置,考虑重力对流场的影响,设置x方向(即混合流体喷射的轴线方向)为重力加速度方向。材料物性参数从Fluent材料库中选择,分别迭代1 000步得到空气和水的模拟结果见图5。

图4 局部网格的加密Figure 4 Mesh encryption of local computational domain

图5 不同流速下的喷雾情况Figure 5 The results of spraying for different flow rate
由图5可知,对于同一喷嘴尺寸,不同流体速度所产生的效果不同,液体喷洒覆盖的范围有相应的差别。当流速增大时,喷嘴以外水沿径向方向扩散的程度变小,水雾扩散半径最大的位置距喷嘴出口的轴向距离变大。流速较慢的情况下,混合流体喷出较短的距离就会与周围空气发生相互作用,产生更为明显的卷吸作用。通过模拟可以得到最大喷洒半径,从而优化设置喷嘴安放的间距;同时最大喷洒半径位置距喷嘴的轴向距离可以为确定喷嘴与传送带的竖直距离提供依据。
如图6所示,压力曲线在喷嘴出口附近有波动,在其余位置基本恒定,符合射流力学中压强与周围流体压强相同的理论[9],即:


图6 喷嘴外部轴向压力分布Figure 6 Distribution of static pressure along axis
4 喷嘴放置位置的优化
对模拟结果进行具体的分析测量,得到入口速度分别为15mm/s和150mm/s时的喷雾各部分尺寸。由于喷洒环境位于室内,且喷洒过程连续无间断,洒水附近区域的空气含水量较高,固模拟过程没有考虑蒸发效应。如图7所示,最大有效喷雾距离为L,假设喷嘴与传送带之间的距离为H,当H<L时,喷出的水雾没有完全散开,效率较低;当H>L时,如果考虑蒸发效应或其他未知因素,则到达传送带上的水汽将会低于预期值。所以设置传送带和喷嘴之间垂直距离的时候,尽量满足H=L。
对于喷嘴安放的密度,由于喷嘴沿传送带的径向排布,为了保证效率的最大化,两个喷嘴之间的距离最大应为2R2,如果间距超过2R2,则喷嘴之间的喷洒区域会出现喷不到的情况;喷嘴最小间距应大于2R1,如果小于这个距离,则喷雾区域重叠过多,喷洒效率下降,需要安放更多的喷嘴。综上所述,合理的喷嘴安置间距应该在R1,R2之间。在初始速度为15mm/s的模拟结果中测量得到R1≈4.44mm,R2≈8.89mm,L≈15mm;150mm/s的测量结果为:R1≈3.36mm,R2≈12mm,L≈30mm。

图7 喷雾尺寸示意图Figure 7 Spray dimensions diagram
5 喷雾试验


图8 试验流程图Figure 8 Test flow chart
由于试验条件的限制,试验测量数值精度较低,由于纸张上湿润部分无法区分R1和R2位置,固不同流速测量喷幅值只有一个,且实际测量值比理论值普遍偏大,考虑是由纸张的吸水性引起的,试验结果见表1。不过整体数值变化的规律与模拟得到的结果吻合较好,由此证明模拟过程是合理的,成功的。

表1 试验结果Table 1 Test results
6 结论
利用Fluent对蛋壳清洗系统的喷水过程进行模拟,采用VOF模型来模拟空气—水的两相流动,并采用标准k—ε模型,在低雷诺数情况下,加入TAB雾化模型分析了离散相。最终得到了15mm/s和150mm/s初始流速条件下的模拟结果,进而利用该结果确定了喷嘴的最优安放位置。
1 段忠意,秦宇辉,刘燕荣.鸡蛋生产环节沙门氏菌检测及洁蛋对蛋品质影响的研究[J].食品安全质量检测学报,2012,3(5):475~480.
2 曹建明.喷雾学[M].北京:机械工业出版社,2005:116~156.
3 冯磊,姚青云.基于VOF模型的泵站压力管道气液两相流数值模拟[J].中国农村水利水电,2012(12):124~126,130.
4 Brackbill J U,Kothe D B,Zemach C.A continuum method for modeling surface tension[J].Computational Physics,1992,100(2):335~354
5 李万平.计算流体力学[M].武汉:华中科技大学出版社,2004:35~56.
6 赵丽君,尹侠.立式三轴搅拌釜—固液悬浮特性的数值模拟[J].食品与机械,2013,29(3):169~172,186.
7 曹仲文,袁惠新.旋流器中分散相颗粒动力学分析[J].食品与机械,2006,22(5):74~76,92.
8 罗辉,孔维梁,刘洪.SLD破碎效应对冰型的影响研究[J].力学季刊,2011,32(4):597~604.
9 董志勇,射流力学[M].北京:科学出版社,2005:23~26.
