水轮机导叶关闭过程的探讨研究

徐晓燕，张晓宏，李建斌

（ 西安理工大学 水利水电学院， 陕西 西安 710048）

1 研究背景

在水电站运行过程中，当水轮机机组瞬间丢弃负荷时，机组转速上升，与此同时在调速器的作用下，快速关闭水轮机导叶又会相应地引起过水系统中水锤压力的上升[1]。 为保证引水系统安全以及机组运行的稳定性，根据调保计算的要求：水锤压力上升的最大值和机组转速上升的最大值都不允许超过规范规定的允许值。 实际上，限制水锤压力升高与限制水轮机机组转速升高的要求往往是相互制约的。 实践证明，与其他因素相比，导叶关闭过程的变化对水锤压力和机组转速的影响更加敏感。 导叶调节过程稍有变化，水锤压力和机组转速会出现明显升降变化。 因此，合理选择水轮机导叶关闭过程是解决甩负荷过程中机组转速上升和蜗壳水压力升高这一矛盾的最经济且有效的措施[2-4]。 本文通过具体的工程实例，针对水轮机导叶的关闭过程进行了深入研究。

2 计算资料简介

某有压引水式电站， 发电引水系统由引水隧洞、两条引水发电支洞、调压室等部分组成。 水库校核洪水位267.70 m，正常高水位263.50 m，死水位为242.00 m。 新扩电站厂房的常遇尾水位为194.00 m。总装机容量为280 MW， 两台机组， 单机的容量为140 MW， 水轮机额定出力143 MW。 最大水头为67.50 m，最小水头为46 m，设计水头为53 m。单机设计水头引用流量296.7 m3/s。 整个系统引水隧洞总长482.03 m，洞径分别为10 m和9.2 m。 调压室为阻抗升管式调压室，调压室的井筒断面是直径为19 m的圆形，其与井底洞段部分通过直径为5.8 m，高度为14.55 m的圆形升管连接。调压室下游两条发电引水支洞即压力管道的长度分别为246.704 m和284.33 m。两条压力管道的洞径都是7.9 m。

3 计算分析

依据计算资料，采用特征线计算方法[4]，建立了与水电站相关的数学模型和水锤方程，编制了计算程序，首先对两台机组同时甩负荷后，导叶按一段直线关闭过程变化情况下的机组转速、蜗壳水锤压力进行计算分析。所得计算结果如表1所示。均不能同时满足：机组转速最大升高率＜45%，蜗壳最大压力升高率＜50%，尾水管真空度＜8 m的要求。

表1 水轮机导叶一段直线关闭过程计算结果Tab. 1 The calculation results of the straight line closing process of one turbine guide vane

目前， 水轮机导叶大多采用两段折线关闭过程[5-10]，所以，下面重点探讨两段关闭情况。

两段关闭过程如图1所示， 第一段关闭时间（ t1）、第二段关闭时间（ t2）和拐点开度（ s）这3个关键因素的取值直接影响着调节保证计算的结果。 为分析两段关闭过程对机组转速和蜗壳水锤压力的影响，分3种情况进行了计算：①第一段关闭时间t1和拐点值s不变，改变第二段关闭时间t2；②第二段关闭时间t2和拐点值s不变，改变第一段关闭时间t1；③第一段关闭时间t1和第二段关闭时间t2不变，拐点值s变化。 部分计算结果如表2及图2—图7所示。

图1 导叶两段关闭示意图Fig. 1 Schematic diagram of closing of two sections ofturbine guide vane

计算结果表2表明：1） 当第一段关闭时间t1和拐点值s不变， 第二段关闭时间t2增加时机组最大转速升高率随着增大， 蜗壳最大水压力升高率下降；反之当第二段关闭时间t2减小时机组最大转速升高率随着减小，蜗壳最大水压力升高率增加。 机组最大转速升高率的增加与第二段关闭时间t2的变化仍近似呈线性关系，而蜗壳最大水压力升高率的减小与第二段关闭时间t2的变化近似呈指数曲线下降。 2） 当第二段关闭时间t2和拐点值s不变，第一段关闭时间t1增加时机组最大转速升高率随之增大，蜗壳最大水压力升高率下降， 反之当第一段关闭时间t1减小时机组最大转速升高率随之减小，蜗壳最大水压力升高率增加。 而且机组最大转速升高率的增加和蜗壳最大水压力升高率的减小与第一段关闭时间t1的变化近似呈线性关系。 3） 当第一段关闭时间t1和第二段关闭时间t2固定不变， 拐点值s增加时机组最大转速升高率随着增大， 蜗壳最大水压力升高率下降，但这种变化为非线性关系。

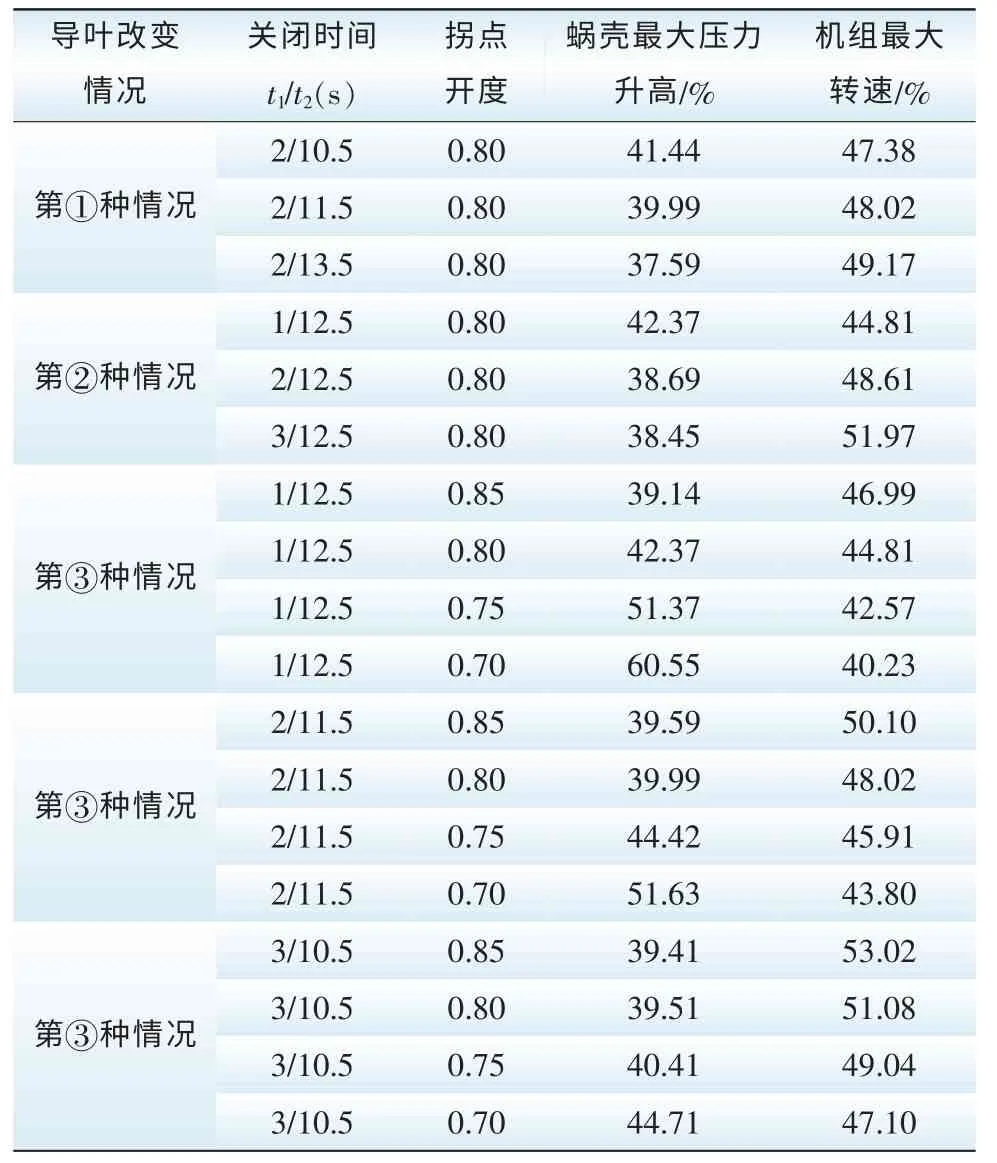
表2 水轮机导叶两段折线关闭过程计算结果Tab. 2 Calculation results of two sections of the turbine guide vane in the closing process

图2 第①种情况蜗壳末端压力变化曲线Fig. 2 The pressure variation curves at the end of the volute in case ①

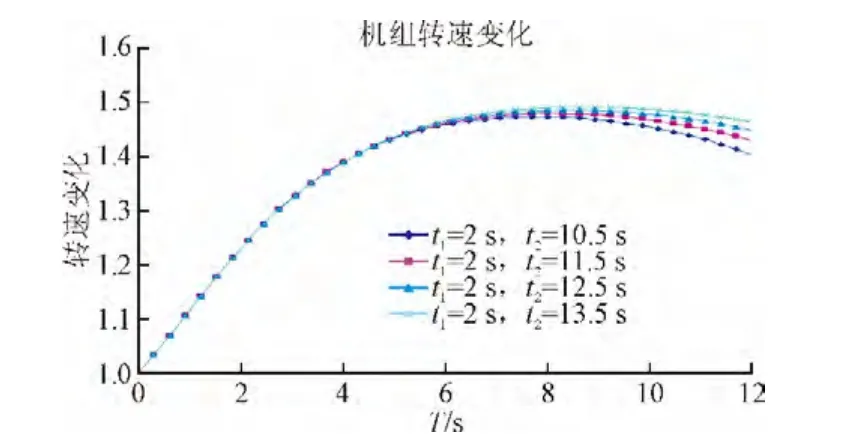
图3 第①种情况机组转速变化曲线Fig. 3 The speed change curves of unit in case ①

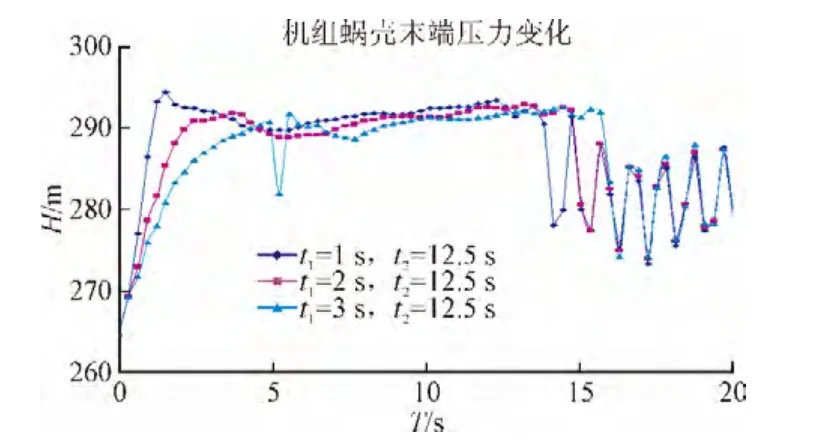
图4 第②种情况蜗壳末端压力变化曲线Fig. 4 The pressure variation curves in case ②at the end of the volute

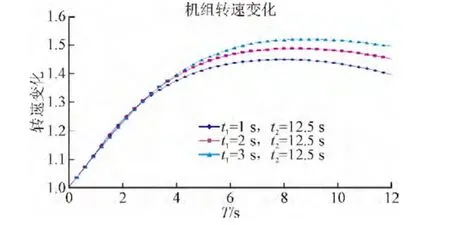
图5 第②种情况机组转速变化曲线Fig. 5 The speed change curves of unit in case ②

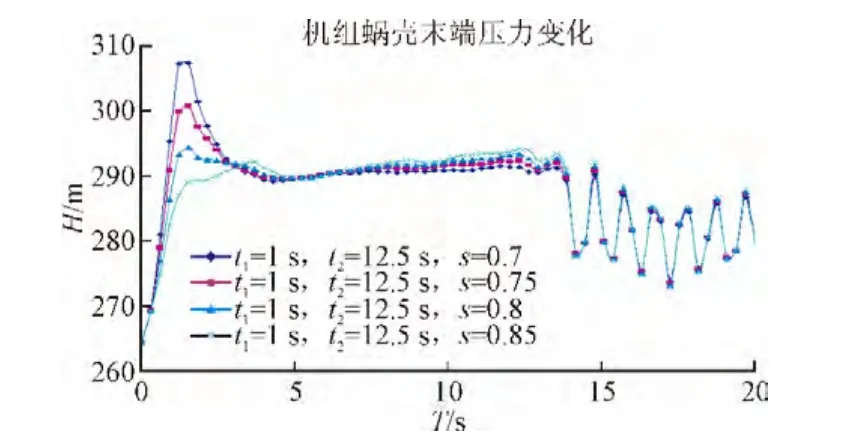
图6 第③种情况蜗壳末端压力变化曲线Fig. 6 The pressure variation curves in case ③at the end of the volute

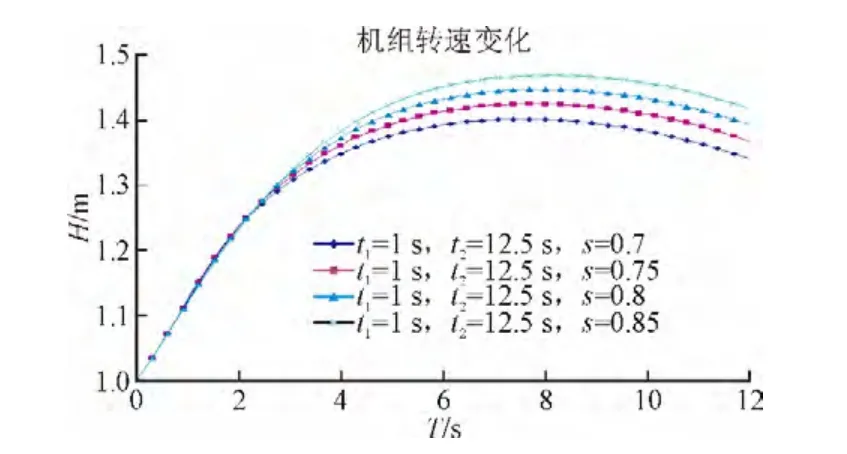
图7 第③种情况机组转速变化曲线Fig. 7 The speed change curves of unit in case ③

4 导叶关闭过程的确定

依据计算结果分析可知，该电站水轮机导叶采用两段关闭过程， 当拟选第一段关闭时间t1为1 s，第二段关闭时间t2为12.5 s，拐点值s为0.8时，两台机组分别在额定水头和最大水头工况下同时甩去全部负荷的过渡过程计算结果为： ①在额定水头下，机组最大转速升高率为44.81%， 蜗壳最大水压力升高率为42.37%，尾水管进口压力－6.01 m。②在最大水头下，机组最大转速升高率为41.51%，蜗壳最大水压力升高率为49.03%，尾水管进口压力－4.29 m。③各项指标数据均能同时满足调节保证计算的要求，能有效解决突然丢弃负荷过程中机组转速上升和蜗壳水压升高之间的矛盾，从而降低了工程造价。

5 结语

本文通过工程实例计算分析了导叶关闭过程中关键因素的变化，探讨了导叶采用两段关闭过程时，第一段关闭时间、第二段关闭时间和导叶位置拐点的改变对水力过渡过程的计算结果产生的影响，通过确定这3个关键值，选择合理的导叶分段关闭模式，得到行之有效的导叶关闭过程，可以更好地协调解决好调保计算中的矛盾问题。

[1] 吴荣樵， 陈鉴治. 水电站水力过渡过程[M]. 北京: 中国水利水电出版社， 1997: 84.

[2] 徐武林， 王煜. 引水式电站过渡过程研究[J]. 能源研究与信息， 2013， 29（ 3）: 139-143.XU Wulin， WANG Yu. Research on the transient process of the diversion-type power station[J]. Energy Research and Information， 2013， 29（ 3）: 139-143（ in Chinese）.

[3] 王丹， 杨建东. 导叶关闭规律及初始开度对蜗壳动水压力的影响[J]. 水电能源科学， 2005， 23（ 4）: 73-75.WANG Dan， YANG Jiandong. Influence of wicket gate closure law of water turbine and initial wicket gate opening on maximun dynamic pressure in spiral case[J].Water Resources and Power， 2005， 23（ 4）: 73-75（ in Chinese）.

[4] 刘启钊. 水电站[M]. 3版. 北京: 中国水利水电出版社，2007.

[5] 张承业. 水轮机导叶两段关闭规律的优化研究[J]. 陕西水利， 2010（ 2）: 133-134.ZHANG Chengye. Study on optimization of the two section closing law of turbine guide vane[J]. Shaanxi Water Resources， 2010（ 2）: 133-134（ in Chinese）.

[6] 杨建东. 导叶关闭规律的优化及对水力过渡过程的影响[J]. 水力发电学报， 1999（ 2）: 75-83.YANG Jiandong. Optimization of wicket closure rule and influence on hydraulic transients for water power station[J].Journal of Hydroelectric Engineering， 1999（ 2）: 75-83（ in Chinese）.

[7] 王慧莉. 导叶两段关闭规律研究[J]. 甘肃水利水电技术，1997（ 3）: 37-39.WANG Huili. Study on the two section closing law of guide vane[J]. Gansu Water Conservancy and Hydropower Technology， 1997（ 3）: 37-39（ in Chinese）.

[8] 楚清河， 杨铁军， 白家骢. 水轮机导叶关闭规律的研究[J]. 河北建筑科技学院学报， 2005， 22（ 2）: 61-64.CHU Qinghe， YANG Tiejun， BAI Jiacong. A simple method of optimization of parameters for hydro guide vanes closed in steps[J]. Journal of Hebei Institute of Architectural Science and Technology， 2005， 22（ 2）: 61-64（ in Chinese）.

[9] 王煜， 田斌. 对水轮机导叶最优关闭规律的探讨[J]. 三峡大学学报： 自然科学版， 2007， 29（ 2）: 113-116.WANG Yu， TIAN Bin. Research for optimizing closing law of wicket gate of hydro-turbines[J]. Journal of China Three Gorge University： Natueal Sciences， 2007， 29（ 2）:113-116（ in Chinese）.

[10] 刘生国. 浅析水轮机导叶两段关闭规律的选择[J]. 水电能源科学， 2009， 27（ 4）: 173-174.LIU Shengguo. Analysis on choice of turbine wicket gate two-slope closing law[J]. Water Resources and Power，2009， 27（ 4）: 173-174（ in Chinese）.