基于ATP-EMTP的电弧接地故障的建模及仿真

王倩，谭王景，叶赞，段建东，崔帅帅

（西安理工大学，陕西 西安 710048）

运行经验表明，电力系统60%以上的故障都是单相接地故障，而其中有相当一部分属于单相电弧接地故障[1]。

早期对单相接地故障的研究，常常将其等同于金属性接地或经一固定阻值的过渡电阻接地[2-4]，但实际上接地点形成的电弧是一个时变非线性的电阻，而且其实际形态常常随着电弧电流、电弧长度以及周围环境产生很大的变化，所以采用上述模型不能准确地反映实际情况。文献[5]首次提出接地故障电弧的精确数字仿真模型，并将其引入一实际220 kV系统，但未考虑配网的可行性。文献[6]提出将Cassie模型应用于模拟电弧接地故障，但只在简单电路中应用其可行性。文献[7]基于近似电弧模型[8]建立接地电弧模型，提出分5个弧长区间建立静态电弧伏安特性模型，但该划分情况对于35 kV和66 kV电网尚待进一步研究。

本文运用弧隙能量平衡理论构建接地电弧模型，在ATP-EMTP上建立用于检验电弧有效性的仿真电路模型，研究了时间常数、耗散功率对电弧特性的影响；其次通过仿真模拟分析间歇性电弧接地故障的发展过程，从而证明接地电弧模型的正确性。

1 接地电弧模型

1.1 电弧数学模型

基于弧隙能量平衡理论[9-10]，可以得到：

将公式（1）进一步转化

式中，g为单位长电弧的电导。

令

则得

考虑到弧长为l的电弧，则式（4）转化为：

式中，u为电弧电压，u=le；P0为电弧弧柱功率损失，

P0=lpLoss。

当电弧弧柱的电导由g转变为稳态电导G时，则电弧稳定燃烧，且电弧输入的能量与散出的相等，即

将式（6）代入式（5），得到

式中，G为电弧稳态电导；g为电弧电导；T为电弧时间常数。

1.2 接地电弧模型

接地电弧模型分为一次电弧和二次电弧[11]。一次电弧由于系统短路接地故障引起，发生在断路器断开前，而二次电弧则是在断路器跳开之后，由于非故障相和故障相间的电磁耦合与静电耦合作用引起[12]。本文重点研究一次电弧，用下标p（primary）表示，则式（7）可写为：

通过以上推导得到关于动态电弧电导gp的非线性微分方程，它基于弧隙能量平衡理论，并且可以很好地体现电弧的物理特征，确定参数TP和Gp就可以求解。

1.2.1 Tp的确定

Tp为电弧时间常数，其物理意义为弧隙中能量变化使弧隙电阻改变2.73倍时所需的时间，Tp反映了电弧伏安特性曲线中电压的上升速度，表示为：

式中，Ip为电弧伏安特性曲线中的峰值电流，可近似采用直接接地时的短路电流；a为常数，一般取2.85×10-5[13]；Lp为电弧长度。

1.2.2 Gp的确定

Gp为一次电弧稳态电导常量，其物理意义为恒定外界条件时，维持电弧燃烧的电弧电导值，表示为：

大量实验研究表明当电弧电流峰值在1.4～24 kA范围内时，电弧压降为15 V/cm。从数据中可以发现电弧压降几乎不发生数值时的变化，因此，可将其进行线性化定值处理；同时Lp也可近似为常数[13]。

1.3 接地电弧的ATP-EMTP模型

基于电弧数学模型，利用ATP-EMTP中的TACS模块来搭建电弧的仿真模型，从而可直观呈现电弧的动态特性。在此仿真模型中，利用TYPE91型TACS可控电阻模块模拟时变的电弧等效电阻。

由于电弧压降Vp、弧长Lp为定值，所以从仿真模型中引入故障点电流的绝对值，并根据式（10）计算得到Gp；同理式（9），系数a、弧长Lp为定值，而Ip可参考统计数据，因此，Tp也可算得。最后，根据上述已求得的Gp、Tp由式（8）计算出电弧电导gp，从而控制TYPE 91型TACS可控非线性电阻阻值的变化规律。流程图如图1所示。

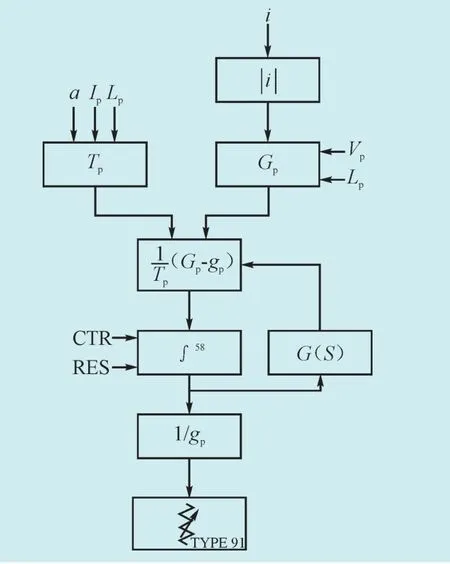
图1 电弧模块流程图Fig. 1 Arc module flow-chart

2 接地电弧仿真分析

2.1 电弧模型的仿真分析

在ATP-EMTP中建立用于检验电弧有效性的实验电路模型，如图2所示。实验电路参数：电源电压u=10 kV，频率f=50 Hz，线路参数r=0.45 Ω/km，L=0.933 7 mH/km，C=0.070 74 pF/km，线路长度为10 km，电弧长度Lp=140 cm，则Ip=1 861 A，VpLp=2 100 V，Tp=3.79×10-4s，仿真时间为0.1 s，结果如图3至图5所示。

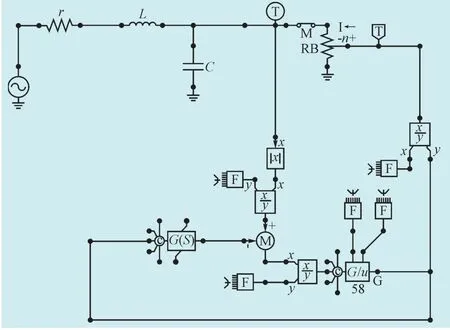
图2 电弧仿真电路模型Fig. 2 Circuit model for the arc simulation

图3 电弧电压仿真波形Fig. 3 Simulation waveform of the arc voltage

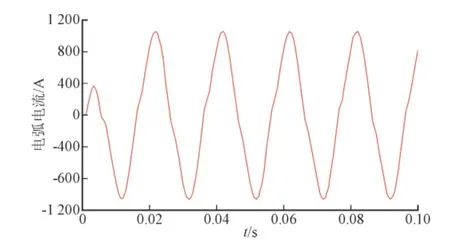
图4 电弧电流仿真波形Fig. 4 Simulation waveform of the arc current

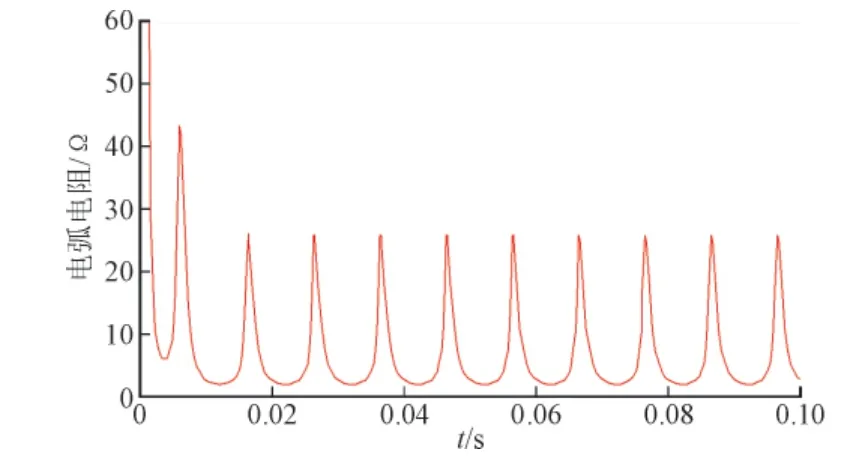
图5 电弧电阻仿真波形Fig. 5 Simulation waveform of the arc resistor

由图3可见，电弧电压波形畸变严重，近似方波，符合“马鞍”形[14]。燃弧后，电压一直降低，直到电弧电流过零。

由图4可见，电弧电流近似为正弦波，但在电流自然过零点前后一小段时间内近似为零，整个这段时间被称为电流“零休”时间。在这段时间内，电弧电流按另外一个规律变化，即电流近似等于电弧电压与电弧电阻的比值，这样，电流就被电弧电阻限制得很小，实际上近似等于零。电弧“零休”与很多因素相关，一是取决于弧隙的内部过程，二取决于外部电路条件，包含电压、电流以及电路常数（电容、电阻、电感）。

由图5可见电弧电阻是时变的，电弧电阻在电流“零休”期间呈现较高阻值，产生尖峰突起。

2.2 电弧特性的影响因素

由前述分析可知，电弧2个主要参数Tp和Gp对电弧的特性起着至关重要的作用。由式（9）、式（10）可以看出Tp和Gp都由电弧长度Lp决定，一旦Lp给定，就可以确定TP和Gp的分母即VpLp。

以下将探讨参数Tp和VpLp的改变对电弧电压、电流、电阻的影响。通过对多组电弧长度Lp进行仿真，研究电弧特性的变化规律。

选取电弧长度Lp=60 cm，则VpLp=900 V，Tp=8.84×10-4s。

通过减小Lp的值，对应于Tp的增大，VpLp的减小，对比图6—9与图3—5可以看出：

图6 电弧电压仿真波形Fig. 6 Simulation waveform of the arc voltage

1）最大燃弧电压降低，由之前的2 842.3 V降低至1 367.9 V，且燃弧后的电压一直在下降。

2）电流值略有增加，峰值由1 058.4 A增大至1 306.6 A，零休时间明显变短。

3）电弧电阻由平均值25.84 Ω下降至3.72 Ω。

选取电弧长度Lp=200 cm，则VpLp=3 000 V，Tp=2.65×10-4s。

图7 电弧电流仿真波形Fig. 7 Simulation waveform of the arc current

图8 电流过零点波形Fig. 8 Waveform of current zero

图9 电弧电阻仿真波形Fig. 9 Simulation waveform of the arc resistor

通过增大Lp的值，对应于Tp的减小，VpLp的增大，对比图10—13与图3—5可以看出：

图10 电弧电压仿真波形Fig. 10 Simulation waveform of the arc voltage

1）最大燃弧电压增加，由2 842.3 V增加至3 961.8 V，且燃弧后的电压一直在下降。

2）电流值略有下降，峰值由1 058.4 A下降至859.61 A，零休时间明显变长。

图11 电弧电流仿真波形Fig. 11 Simulation waveform of the arc current

图12 电流过零点波形Fig. 12 Waveform of current zero

图13 电弧电阻仿真波形Fig. 13 Simulation waveform of the arc resistor

3）电弧电阻由平均值25.84 Ω增大至89.997 Ω。

表1 对比不同电弧长度时的仿真结果Tab. 1 Comparison of simulation results for arcs of different lengths

通过仿真分析可知，电弧长度LP的减小，参数Tp增大，对应于电弧电压下降，电弧零休时间减弱，电弧电阻平均阻值减小，这是因为Tp增大后，对应的功率损失降低，表示电弧向外散出的热量减少，从而弧柱中储存的能量增多，使得电弧过零点时变得不易熄弧。

随着电弧长度LP的增大，参数Gp减小（VpLp增大），对应于电弧电压增加，电弧零休时间增强，平均阻值增大，这是因为对应的功率损失增加，表示电弧向外散出的热量增大，从而弧柱中储存的能量减小，使得电弧过零点时变得容易熄弧。

文中选取电弧长度Lp为140 cm时的参数用于之后的仿真。

3 间歇性电弧接地故障仿真

间歇性电弧接地现象可由高频熄弧理论和工频熄弧理论来解释。高频熄弧理论认为高频振荡电流第一次过零时电弧熄灭，半个工频周期之后重燃。而工频熄弧理论认为工频电流过零时电弧熄灭。工频理论分析所得过电压值较接近于实际情况[15]。因此本文采用工频熄弧理论来分析弧光接地过电压。

为了验证仿真的有效性，引入某10 kV配电网系统，根据实测结果，空载系统发生单相接地故障时过电压最严重，因此仅对空载系统进行仿真分析，将35 kV系统前的部分网络等效为理想电源，而变压器采用理想的等效变压器，该系统共5条出线，1条架空线，4条电缆出线系统如图14所示。

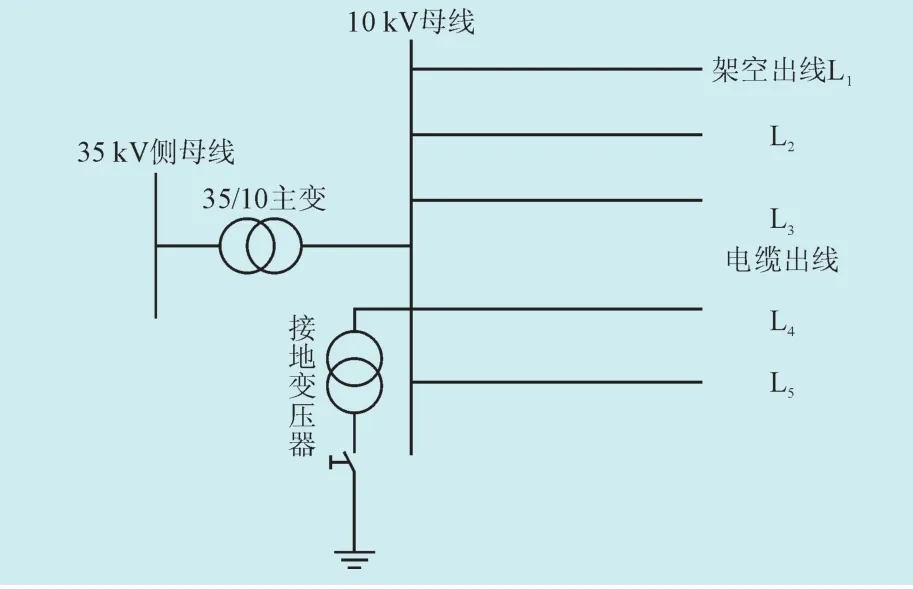
图14 某10kV配电网系统Fig. 14 A 10 kV distribution network system

在架空出线L1末端发生间歇性电弧接地故障，从最严重的情况考虑，A相电压为正或负峰值时刻，A相发生单相接地故障。使用第1节的接地电弧模型对间歇性电弧接地故障进行仿真。在A相与电弧模型之间设置一个开关，开关闭合模拟电弧接地故障，开关断开模拟故障消除或电弧熄灭。半个工频周期后，电流过零认为是工频电流过零，此时开关断开模拟电弧熄灭；熄弧之后故障相的第一个峰值时刻电弧重燃，此时开关闭合。从时间上看，工频熄弧是每隔一个工频周波重燃一次。0.028 35 s模拟第一次接地故障，0.038 35 s开关断开。此后开关闭分时间分别为0.048 35 s，0.058 35 s，0.068 35 s，0.078 35 s。即为3次重燃、3次熄弧的工频过电压仿真。

由图15、图16可知，在燃弧和熄弧的过程中，系统中能量的积聚是产生间歇性电弧接地过电压的重要因素，系统每次发生电弧接地都会引起高频振荡，产生过电压，而电压随着重燃次数的增加而增加，可以看到非故障相和中性点上出现的最大过电压分别为3.35 pu和2.38 pu，符合不考虑泄漏、相间电容时的彼得生工频熄弧理论[16]，从而证明了接地电弧模型的正确性。

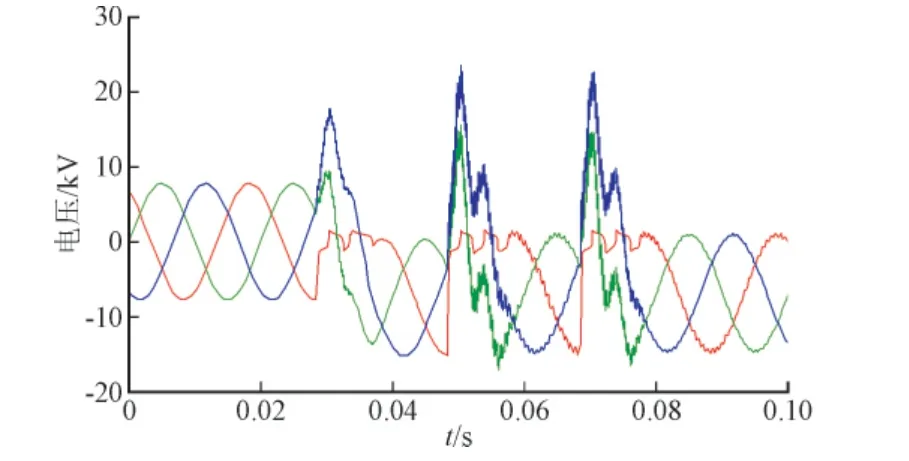
图15 10 kV系统3次燃熄弧故障点电压波形Fig. 15 Fault point voltage waveform of three times of arc reigniting and extinguishing in the 10 kV system

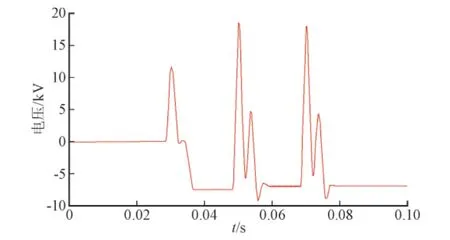
图16 10 kV系统3次燃熄弧中性点电压波形Fig. 16 Neutral point voltage waveform of three times of arc reigniting and extinguishing in the 10 kV system

4 结论

本文针对间歇性弧光接地过电压，提出基于弧隙能量平衡理论的接地电弧模型，并讨论了模型中TP和GP的影响结果。

1）基于电弧数学模型，利用ATP-EMTP中TACS模块搭建电弧仿真模型，完成了电弧动态特性直观呈现。

2）获得了时间常数、耗散功率对电弧特性的影响规律，为电弧参数选取提供依据。

3）利用所建立的模型对间歇性电弧接地故障进行了防真研究，验证了其有效性。

[1] HUA Ren，LI Xiaohui，STADE D，et al. Arc fault model for low-voltage AC systems[J]. IEEE Transactions on Power Delivery，2005，20（2）: 1204-1205.

[2] 王艳松，解飞. 配电网单相接地故障的仿真分析[J]. 高电压技术，2008，34（1）: 123-127.WANG Yansong，XIE Fei. Simulation and analysis of single phase to ground fault in distribution networks[J]. High Voltage Engineering，2008，34（1）:123-127（in Chinese）.

[3] 蔡维，王华荣，刘承志，等. 中性点不揍地电网单相接地故障特征仿真研究与新结论[J]. 电力自动化设备，2006，26（2）：33-36.CAI Wei，WANG Huarong，LIU Chengzhi，et a1. Simulation of single. phase grounding fault on non-grounding neutral power system and new conclusions[J]. Electric Power Automation Equipment，2006，26（2）: 33-36（in Chinese）.

[4] 齐郑，杨以涵. 中性点非有效接地系统单相接地选线技术分析[J]. 电力系统自动化，2004，28（14）: 1-5.QI Zheng，YANG Yihan. Analysis of technology of fault line selection for single-phase-to-earth faults in neutral point non-effective grounded system[J]. Automation of Electric Power Systems，2004，28（14）: 1-5（in Chinese）.

[5] 康健. 接地故障电弧的精确数字仿真及其计算[J]. 继电器，2002，30（5）: 14-16.KANG Jian. Exact digital simulation and calculation of fault arcs[J]. Relay，2002，30（5）: 14-16（in Chinese）.

[6] 于然，付周兴，王清亮，等. 基于MATLAB的电弧建模仿真及故障分析[J]. 高压电器，2011，47（9）:95-99，106.YU Ran，FU Zhouxing，WANG Qingliang，et al. Modeling simulation and fault analysis of arc based on matlab[J].High Voltage Apparatus，2011，47（9）: 95-99，106（in Chinese）.

[7] 顾荣斌，蔡旭，陈海昆，等. 非有效接地电网单相电弧接地故障的建模及仿真[J].电力系统自动化，2009，33（13）:63-67.GU Rongbin，CAI Xu，CHEN Haikun，et al. Modeling and simulating of single-phase arc grounding fault in noneffective earthed networks[J]. Automation of Electric Power Systems，2009，33（13）: 63-67（in Chinese）.

[8] 胡平. 可用于分析矿井电网单相电弧性接地过电压的近似电弧模型[J]. 煤炭学报，1992，17（2）: 80-88.HU Ping. An arc model for analyzing overvoltage caused by one phase arc-grounded failure in mine power supply system[J]. Journal of China Coal Society，1992，17（2）:80-88（in Chinese）.

[9] 王仁甫. 电弧现象模型的发展[J]. 高压电器，1991，27（4）：39-46.WANG Renfu.Arc phenomenon model and its developing[J].High Voltage Apparatus，1991，27（4）:39-46（in Chinese）.

[10] 王其平. 电器电弧理论[M].北京:机械工业出版社，1991.

[11] DJURIC M B，TERZIJA V V. A new approach to the arcing faults detection for fast autoreclosure in transmission systems[J]. IEEE Transactions on Power Delivery，1995，10（4）: 1793-1798.

[12] LIN Xin，HE Baina，XU Jianyuan. Secondary arc spectrum characteristics on EHV transmission lines[J]. High Voltage Engineering，2009，35（8）: 1891-1895.

[13] JOHN S A T，AGGARWAL R K，SONG Y H. Improved techniques for modeling fault arcs on faulted EHV transmission systems[J]. IEE Proceedings-Generation，Transmission and Distribution，1994，141（2）: 148-154.

[14] ELKALASHY N I，LEHTONEN M. Modeling and experimental verification of high impedance arcing fault in medium voltage networks[J]. IEEE Transactions on Dielectrics and Electrical Insulation，2007，14（2）: 375-383.

[15] 李福寿. 中性点非有效接地电网的运行[M]. 北京: 水利电力出版社，1993.

[16] PETERSEN W. Arcing grounds （Intermittent Ground Faults）[J]. Elektro Technishe Zeitschrift，1917，38: 553-564.