级联H桥型多电平逆变器的CPS-SPWM调制策略研究
2015-12-20张贞艳仲伟松
张贞艳,仲伟松
(宿迁学院,江苏 宿迁 223800)
级联H桥型多电平变换器[1-2]是所有多电平逆变器中出现最早的一种。早在1975年,美国P.Hammond就提出了多个H桥单元采用独立的直流电源作输入、输出端串联的级联型逆变器结构,并申请了专利。限于当时背景,并没受到重视。逐渐迫于对中高压大容量逆变器的巨大需求,级联H桥型逆变器才受到关注。发展至今,其已被广泛应用于高压电机驱动、高压大功率电源、高压大功率有源电力滤波等众多场合。
载波相移正弦脉宽调制(carrier phase-shifted,CPS-SPWM)技术是在传统的SPWM调制技术的基础上发展起来的一种多重化技术,是一种适用于大功率电力开关变流器的优秀调制策略[3]。因其等效开关频率高、传输带宽宽、输出线性度好、控制性能优等优点备受追捧。其中双极性CPS-SPWM和单极倍频CPS-SPWM为2种常用的调制方法[4]。本文针对这2种调制方法展开详细的对比研究。
1 双极性CPS-SPWM技术
1.1 双极性CPS-SPWM调制原理
三相Y型连接的级联H桥型多电平逆变器拓扑如图1所示,该逆变电路每相级联N个H桥单元,各H桥单元均采用独立的直流电源供电。
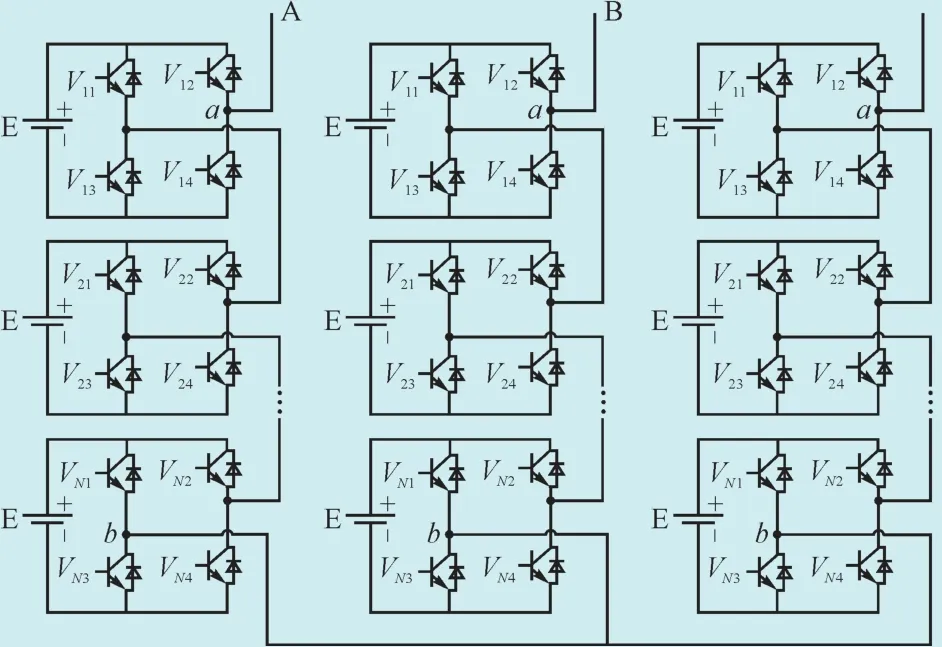
图1 级联H桥型多电平逆变器拓扑Fig. 1 Topology of the multilevel converter based on cascaded H-bridge
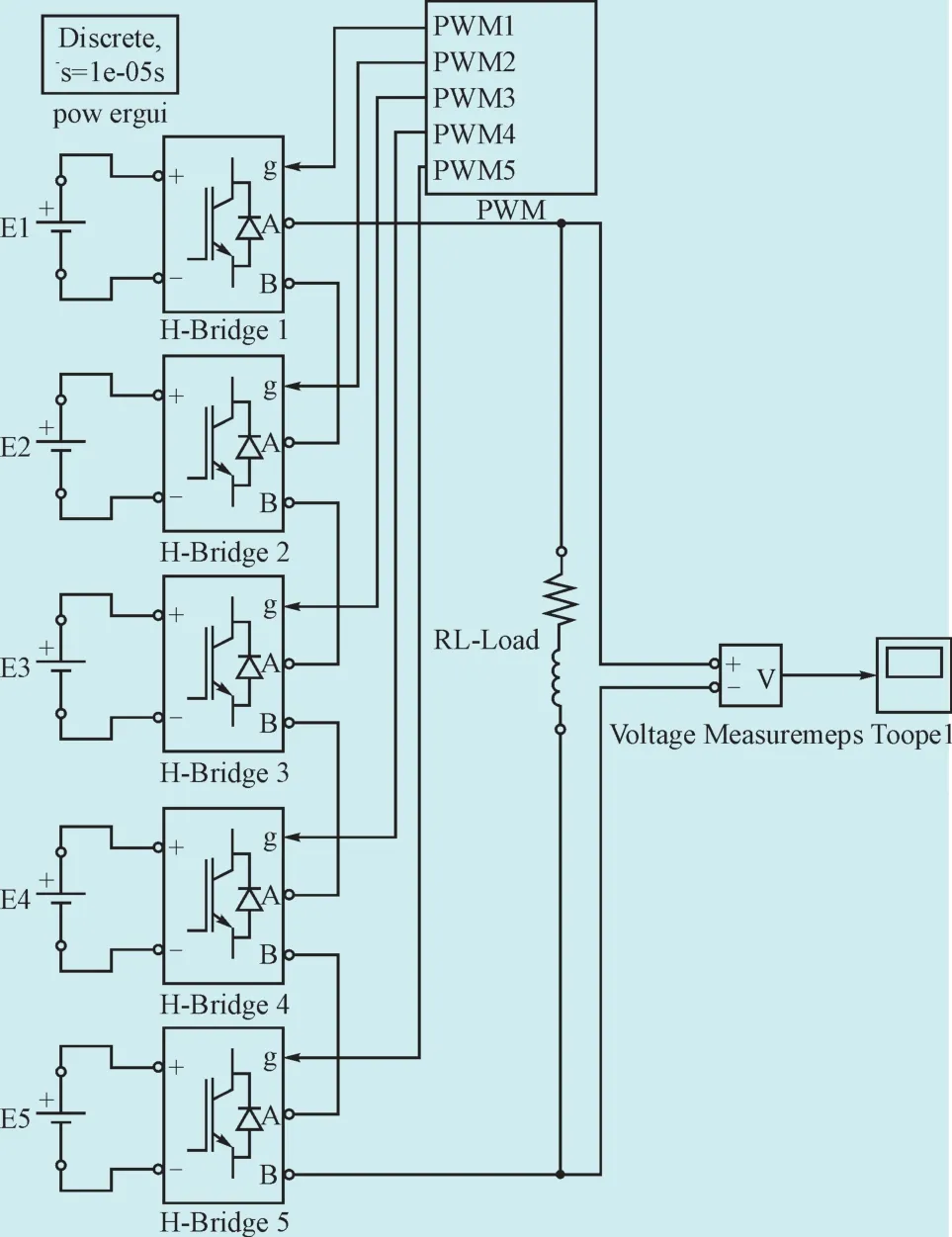
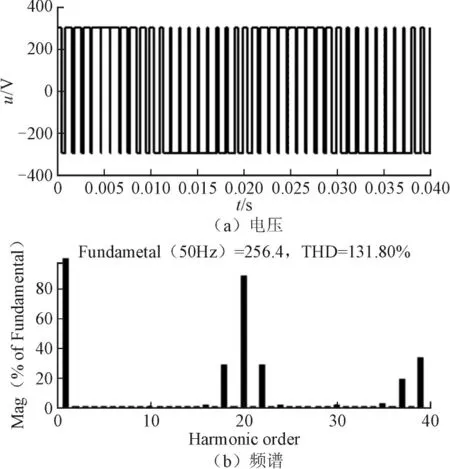
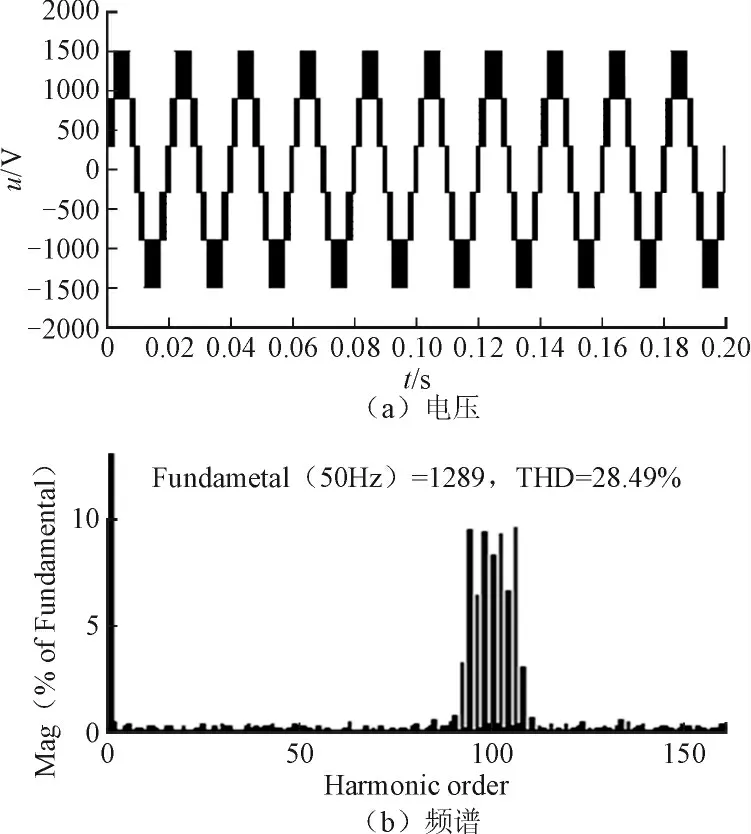
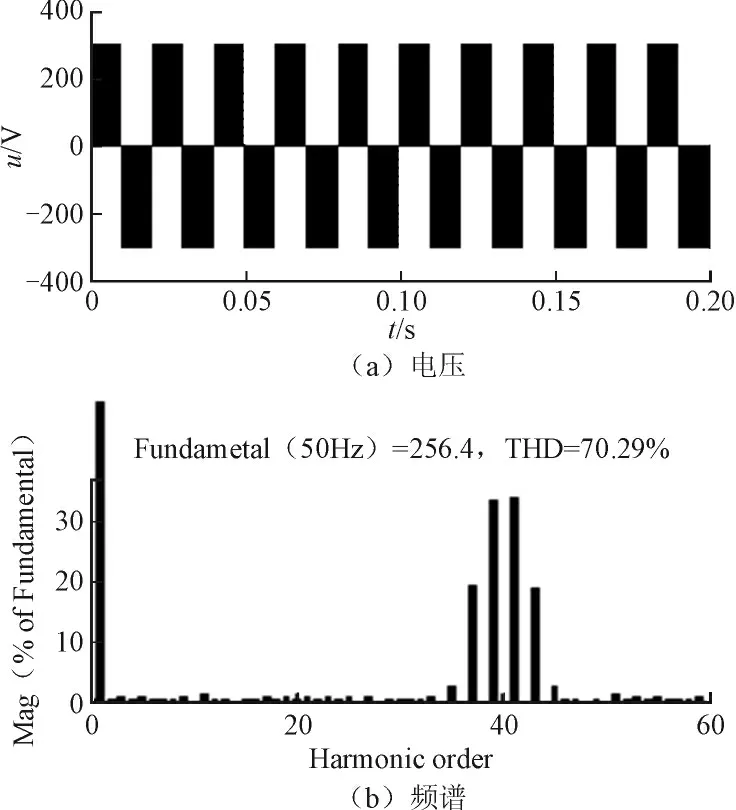
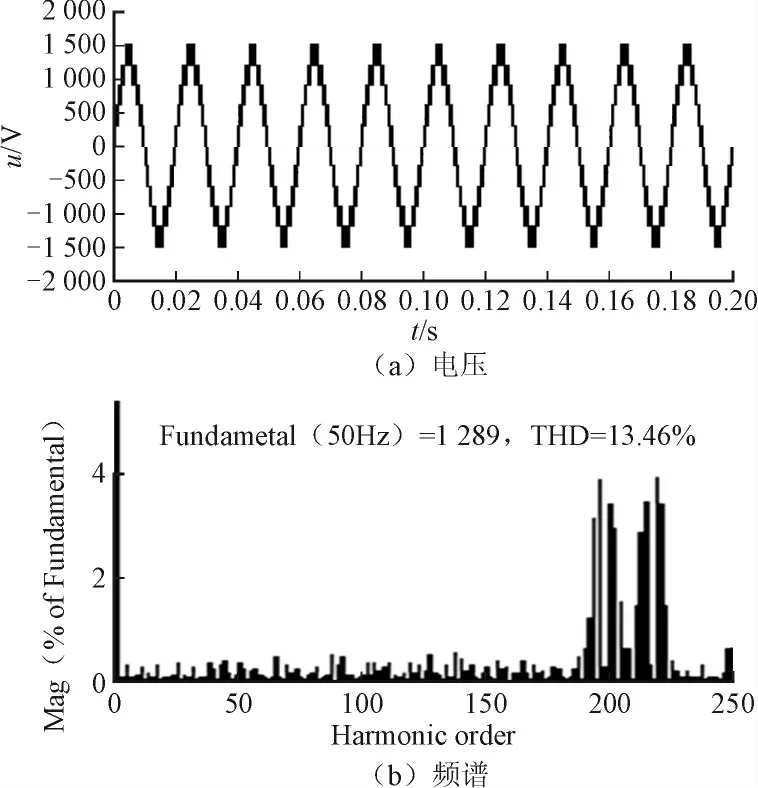
以A相为例,阐述双极性CPS-SPWM调制原理:对该相级联的N个H桥单元均采用双极性SPWM调制策略。比如,针对第1个H桥单元,将频率为ωs的正弦调制波us与频率为ωc的三角载波uc1相比较,us>uc1时,所得驱动信号g驱动开关管V11和V14;us 设A相所采用的调制波为us(t)=Ussin ωst,幅值为Us,频率为ωs,初相角为0;三角载波的幅值为Uc,频率为ωc,初相角为0;令调制度M=Us/Uc,频率调制比kc=ωc/ωs,采用双极性SPWM调制,对第1个H桥单元的输出电压波形按照双重傅里叶级数展开,其表达式为: 式中:J0、Jn分别为零阶Bessel函数和n阶Bessel函数,E为H桥单元直流侧电压,以下同。 此时,A相逆变器总输出电压的双重傅里叶级数表达式为: 通过对式(1)和式(2)的对比分析得出:U1(t)和U(t)均包含3部分。定义式中仅与调制波频率ωs有关的第一项为基波分量,定义式中仅与载波频率ωc有关的第二项为载波谐波;定义式中与ωs、ωc都有关的第三项为边带谐波;比较式(1)和式(2)不难看出逆变器输出电压中,总的基波分量是单个H桥单元输出电压基波成分的N倍,即级联后总输出电压无基波损失;单个H桥单元输出的次数最低的谐波群出现在kc次及其边频附近,而级联后总的输出电压中只含奇次谐波,且最低次的谐波群出现在Nkc次附近,相当于将功率器件的等效开关频率提高了N倍,从而较大地降低了器件的开关损耗,有效改善了输出电压的波形质量。 同样A相为例,阐述单极倍频CPS-SPWM调制原理:对该相级联的N个H桥单元均采用单极倍频SPWM调制策略,本文采用载波反相法实现倍频输出,即每个H桥单元需正反两列三角载波;比如,针对第1个H桥单元,需要三角载波uc1及反相于uc1的三角载波;调制波us与uc1相比较,us>uc1时,所得驱动信号g驱动开关管V11,其互补信号驱动开关管V13;调制波us与相比较,us>时,所得驱动信号g′的反相信号驱动开关管V12,g′来驱动开关管V14。第2、3、…、N个H桥单元的调制原理与第1个H桥单元相同,且均采用同一列调制波us;采用的三角载波分别为uc2、uc3、…、ucN,及其对应的反相信号、…,频率均为ωc,相位依次错开三角载波周期的1/2N,例如第1列三角载波uc1的相位为φc1,则第i列三角载波uci的相位φci=φc1+π(i-1)/N;将N个H桥单元的输出叠加即得A相逆变器总的输出电压,其电平数为2N+1。 设A相所采用的调制波为us(t)=Ussin ωst,幅值为Us,频率为ωs,初相角为0;第一个H桥单元的三角载波共两列,幅值为Uc,角频率为ωc,初相角分别为0和π;对图1中第一个H桥单元的输出电压波形进行双重傅里叶级数展开,其表达式为: 此时,A相逆变器总输出电压的双重傅里叶级数表达式为: 通过式(3)和式(4)的对比分析得出:级联后总输出电压的基波分量是单个H桥单元输出电压基波成分的N倍,即级联后无基波损失,这一点和双极性CPS-SPWM调制相同;单个H桥单元输出的次数最低的谐波群出现在2kc次及其边频附近,而级联后总的输出电压最低次谐波群出现在2Nkc次附近,相当于将功率器件的等效开关频率提高了2N倍,大大降低了功率器件的开关损耗,大大改善了输出电压的波形质量。 为了验证以上数学分析的正确性,在MATLAB中搭建了单相级联H桥型多电平逆变器的仿真模型,如图2所示(三相逆变器实现原理和单相的类似,只不过每相采用的调制波相位要依次错开120度,这里不作赘述)。模型主要包含级联H桥型逆变器模块、PWM生成模块及RL串联负载;其中逆变器模块由5个H桥单元级联而成,即N=5,每个H桥单元均由独立的直流电源供电。 图2 基于级联H桥的单相逆变器仿真模型Fig. 2 The simulation model of the single-phase converter based on cascade H-bridge 采用双极性CPS-SPWM调制方式时,图2中PWM生成模块的内部结构,如图3所示;采用单极倍频CPS-SPWM调制方式时,图2中PWM生成模块的内部结构,如图4所示。 对图3,根据双极性CPS-SPWM调制原理,对于5单元级联的H桥型逆变器,需5列载波,生成10路脉冲信号来驱动5个H桥单元的功率管,能得到6电平输出。三角载波相位角依次互差2π/5,仿真中通过设置Transport Delay~ Transport Delay4 实现载波相位移动。 对图4,根据单极倍频CPS-SPWM调制原理,采用载波反相法实现倍频输出,对于5单元级联的H桥型逆变器,需要10列载波,生成20路脉冲信号来驱动5个H桥单元的功率管,能得到11电平输出。三角载波依次互差π/5,仿真中通过设置Transport Delay~Transport Delay4 实现载波相位移动。 图3 双极性CPS-SPWM生成模块Fig. 3 Bipolar CPS-SPWM module 为了便于对比,设置仿真参数如下,H桥单元直流侧电压E=300 V,调制波频率50 Hz,载波频率1 000 Hz,调制度M=0.86,R=26 Ω,L=3 mH。 采用双极性CPS-SPWM调制方式时,得到逆变器的第1个H桥单元的输出电压和频谱如图5所示,逆变器总的输出电压和频谱如图6所示。 由图5可见,采用双极性调制方式,H桥逆变器单元的输出电压包含2种电平,输出电压的基波有效值为256.4 V,为M倍的直流侧电压E,总谐波畸变率为131.8%,次数最低的谐波群出现在20次及其边频附近,验证了出现在kc次附近的结论。由图6可见,5单元级联的H桥型逆变器总的输出电压包含6电平,输出电压的基波有效值为1 289 V,为NM倍的直流侧电压E,验证了级联之后无基波损失;输出电压总谐波畸变率为28.49%,次数最低的谐波群出现在100次附近,验证了出现在Nkc次附近、即将装置的等效开关频率提高了N倍的结论。仿真结果验证了所做数学分析的正确性,双极性CPS-SPWM调制策略具有良好的消除谐波的性能。 采用单极倍频CPS-SPWM调制方式时,得到逆变器第1个H桥单元的输出电压和频谱如图7所示,逆变器总的输出电压和频谱如图8所示。 图5 H桥单元输出电压和频谱Fig. 5 The output voltage and its spectra of H-bridge unit 图6 逆变器输出电压和频谱Fig. 6 The output voltage and its spectra of inverter 图7 H桥单元输出电压和频谱Fig. 7 The output voltage and its spectra of H-bridge unit 图8 逆变器输出电压和频谱Fig. 8 The output voltage and spectra of converter 由图7可见,采用单极倍频调制方式,H桥单元的输出电压包含3种电平,输出电压的基波有效值为256.4V,为M倍的直流侧电压E,这一点和采用双极性调制相同;但是电压总谐波畸变率为70.29%,相比较图5(b)的131.8%显著减小;次数最低的谐波群出现在40次及其边频附近,验证了出现在2kc次附近的结论。由图8(a)可见,5单元级联的H桥式逆变器总的输出电压包含11电平,与图6(a)相比,波形更接近正弦波,且每个等级的电压值都大大降低,因而电压变化率更低,输出电压中的谐波含量更少,输出电压的基波有效值同样为1 289 V,即NM倍的直流侧电压E,这一点和双极性CPS-SPWM相同,即不会造成基波损失;但是总谐波畸变率为13.46%,相比较图5(b)的28.49%明显减小。次数最低的谐波群出现在200次附近,验证了出现在2Nkc次附近、即将装置的等效开关频率提高了2N倍的结论。仿真结果充分验证了所做数学分析的正确性,和双极性CPS-SPWM调制策略相比,单极倍频CPS-SPWM调制策略具有更好的消除谐波的性能。 本文首先介绍了载波相移CPS-SPWM调制策略在大功率场合的具体应用;详细介绍了双极性CPSSPWM和单极倍频CPS-SPWM的调制原理,又进行了详细的数学分析,得出双极性CPS-SPWM调制能将功率器件的等效开关频率提高N倍,而单极倍频CPS-SPWM调制能将功率器件的等效开关频率提高2N倍,单极倍频CPS- SPWM比双极性CPS-SPWM的输出波形更接近正弦波,消除谐波特性更好的结论;最后通过建模进行了仿真,利用频谱分析法进行了对比分析,验证文中所做理论分析和数学分析的正确性。 [1] 刘敬珺. H桥级联型多电平逆变器的研究[D]. 上海:上海交通大学,2011. [2] 姜旭. H桥级联式SSSC主电路拓扑分析及控制策略研究[D]. 北京:华北电力大学,2007. [3] 许湘莲. 基于级联多电平逆变器的STATCOM及其控制策略研究[D]. 武汉:华中科技大学,2006. [4] 常志琴,孙丽玲,谢欢. H桥级联SVG的载波移相调制技术研究[J]. 电测与仪表,2015,51(4): 66-72.CHANG Zhiqin,SUN Liling,XIE Huan. Research on H bridge cascaded svg with carry phase shifting technology[J].Electrical Measurement & Instrumentation,2015,51(4):66-72(in Chinese). [5] 何兰萍. 基于级联H桥的无功发生器的研究[D]. 合肥:安徽理工大学,2011. [6] 段海雁,段海兵.SVG动态无功补偿装置在高线轧钢生产线的应用[J]. 电力电容器与无功补偿,2014(4): 26-31.DUAN Haiyan,DUAN Haibing. Application of SVG dynamic reactive power compensation device in wire rod rolling mill line[J]. Power Capacitor & Reactive Power Compensation,2014(4): 26-31(in Chinese). [7] 李银,罗朋,冯学俊,等. 载波层叠调制技术在6 kV级联STATCOM中的应用[J]. 电力电容器与无功补偿,2014(6): 1-4.LI Yin,LUO Peng,FENG Xuejun,et al. Application of carrier lamination modulation technology in 6 kV cascade STATCOM[J]. Power Capacitor & Reactive Power Compensation,2014(6): 1-4(in Chinese). [8] 游力,周易,陈乔夫. 基于SVPWM的串联混合型有源电力滤波器的研究[J]. 电力电容器与无功补偿,2015(1):39-43.YOU Li,ZHOU Yi,CHEN Qiaofu. Research on the series hybrid active power filter based on SVPWM[J]. Power Capacitor & Reactive Power Compensation,2015(1): 39-43(in Chinese). [9] 谭玉茹,苏建徽. 基于移相载波的模块化多电平换流器控制方法研究[J]. 高压电器,2012,48(8): 56-64.TAN Yuru,SU Jianhui. CPS-SPWM based control strategy for modular multilevel converter[J].High Voltage Apparatus,2012,48(8): 56-64(in Chinese).1.2 双极性CPS-SPWM的双重傅里叶分析
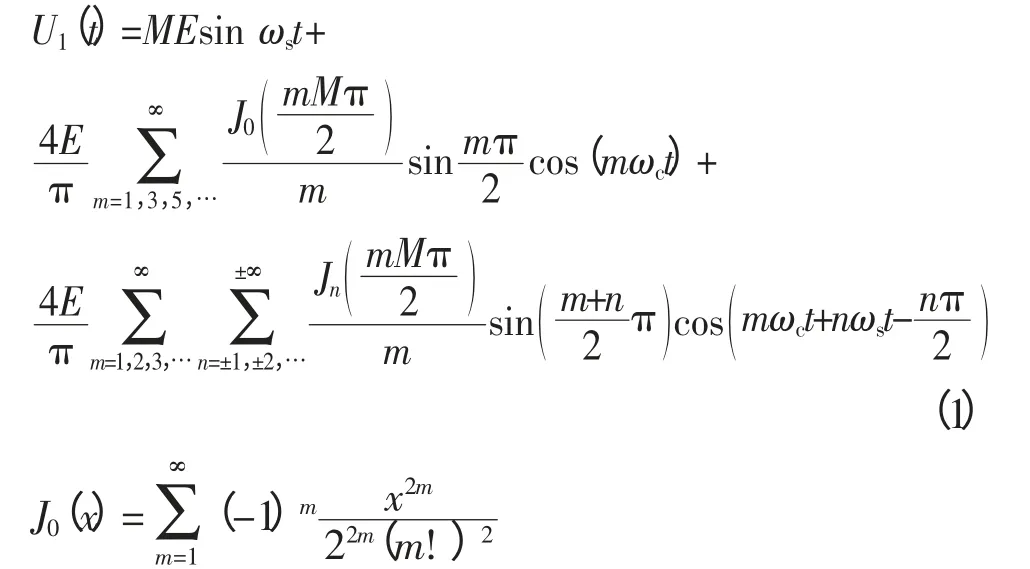
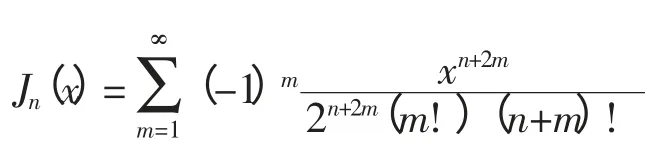
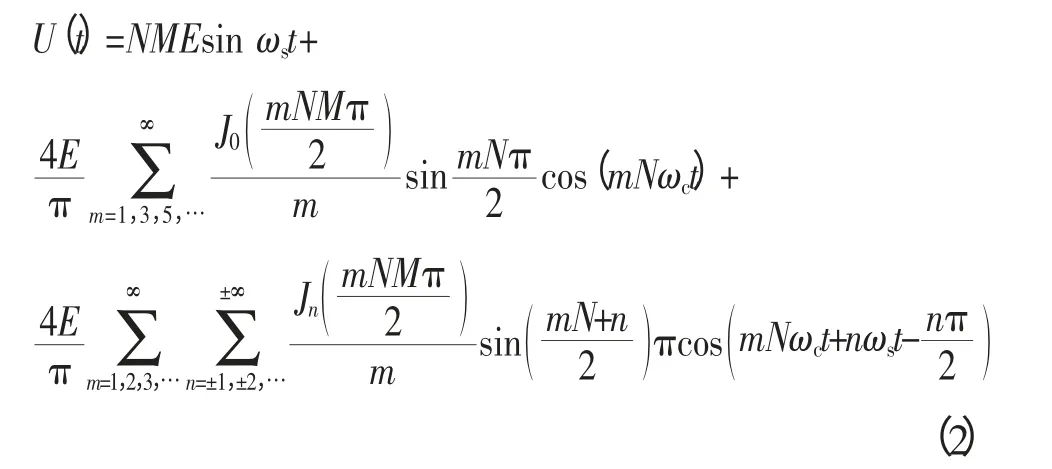
2 单极倍频CPS-SPWM技术
2.1 单极倍频CPS-SPWM调制原理
2.2 单极倍频CPS-SPWM的双重傅里叶分析
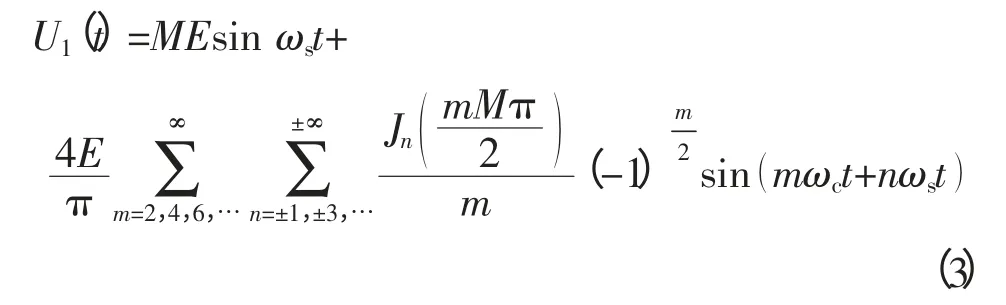

3 仿真模型
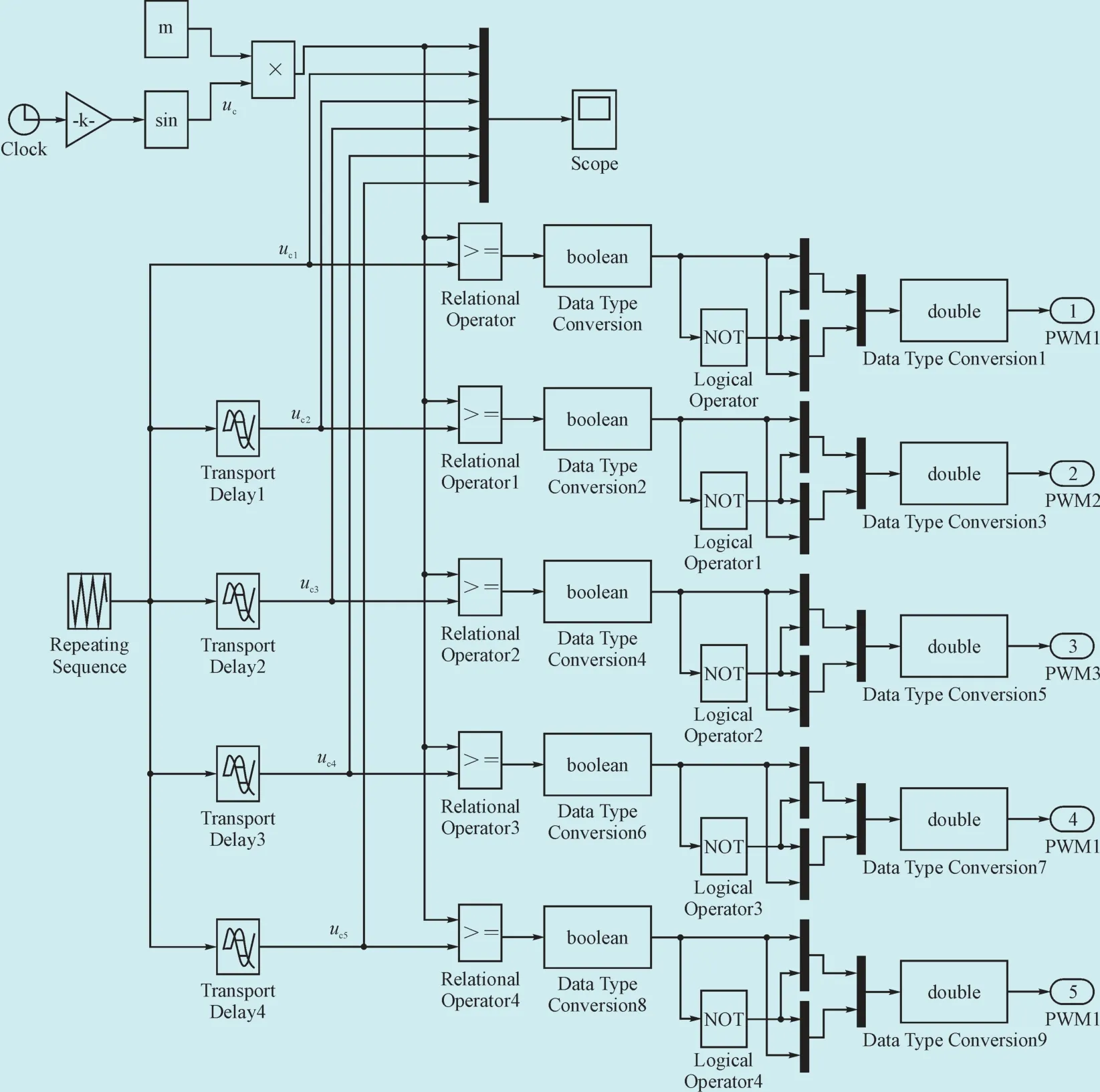
4 波形分析
5 结语
