精确击穿电弧模型仿真及分析

王倩，叶赞，谭王景，段建东，崔帅帅，李笑

（西安理工大学自动化与信息工程学院，陕西西安 710048）

随着配电网电缆线路比重的提高，当电缆发生故障时将会严重影响系统的稳定性。造成电缆故障的原因有多种，为了能够对电缆故障进行分析，就有必要研究故障点的电弧特征。而创造一个实验环境来模拟故障电弧花费较高，在一个实际的电力系统上模拟故障电弧，代价昂贵且操作起来很不安全，同时来模拟“可重复性”接地故障几乎是无法实现的。因此，建立故障电弧的仿真模型对于故障分析显得尤为重要。

当前的电弧模型有黑盒模型和物理模型。黑盒模型基于弧隙能量平衡原理，应用数学方法加以描述，形成可进行数学求解的方程式，对能量转换有更精确的描述[2]。在物理电弧模型的发展过程中，Cassie、Mayr模型均表达了电弧电压、电弧电流、电弧电导、时间常数、能量损失之间的关系，其中将时间常数和能量损失看作常数[3-4]。由于电弧具有复杂性和随机性的特征，当前的电弧模型不能够完整准确地从物理概念说明电弧的本质，大多用于定性分析。

本文在三段式击穿电弧理论分析与理解的基础上，利用ATP-EMTP仿真软件分别建立了基于压控时变电阻的三段式击穿电弧模型和基于TACS三段式击穿电弧模型，对基于TACS电弧模型进行改进，采用提取击穿时刻的方法精确建模，并对2种电弧模型进行仿真对比[5-9]。

1 三段式击穿电弧

1.1 理论分析

文献[6-8]中的电弧模型分别提出并论证了电弧的纯电阻特性。但是有些电弧模型需先鉴别电弧状态是否稳定，然后才可在稳定燃烧时考虑电弧的纯电阻特性。有些尽管不需鉴别，但是没有考虑电弧的起弧、燃弧和熄弧过程中的3个阶段持续时间的随机性及其电弧电阻的动态变化问题。

电缆故障点击穿至产生电弧可以分为3个阶段[9-10]：

1）击穿起弧阶段。当故障点的电压达到一定数值时，将使故障点击穿，击穿过程中电压又将振荡减小，电流逐渐增大。

2）燃弧阶段。故障点被击穿后电弧呈现稳定低电阻特性，故障点电压电流基本符合直流特性。

3）熄弧阶段。电压电流剧烈震荡直至电弧消失，故障点恢复为原来状态。

击穿起弧阶段和熄弧阶段的电压电流不稳定，有着剧烈的振荡变化，击穿起弧阶段持续时间一般会在200～300 μs之间，熄弧阶段持续时间在300～400 μs之间，而燃弧阶段的电弧有明显的电阻特性，且电弧的电压和电流变动较小，具体变化方式和持续时间取决于电路的连接方式及电弧本身的伏安特性，持续时间一般在800～1 200 μs之间[9]。

1.2 模型的构建

根据文献[9]中提供的电弧击穿特性参数，本文直接统计出了3个阶段的电阻值：起弧和熄弧阶段电弧电阻随机剧烈变化，在0～3 kΩ范围内变化；燃弧阶段的电阻从0 Ω指数增加到100 Ω左右。各个阶段持续时间已经给出。

电弧电阻模型为：

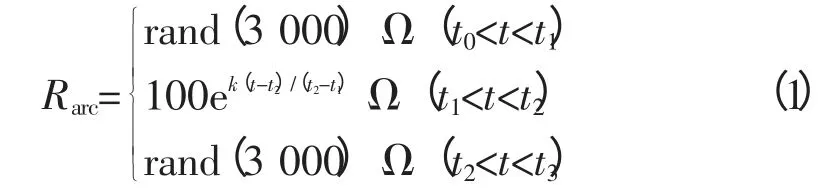
式中：t0为电弧达到击穿电压的起始时间；t1为起弧阶段的结束时间，起弧阶段持续时间250 μs±rand（50）μs；t2为燃弧阶段的结束时间，燃弧阶段持续时间1 000 μs±rand（200）μs；t3为熄弧阶段的结束时间，熄弧阶段持续时间350 μs±rand（50）μs；rand（3 000）为随机生成一组1～3 000之间的随机数；k为递增系数（待求）。

2 基于压控时变电阻和TACS开关的击穿电弧模型

2.1 基于压控时变电阻的三段式击穿电弧模型

压控时变电阻，当电阻端电压小于设定的击穿电压时，电阻电路断开；当电阻端电压大于设定的击穿电压时（同时要满足时间大于设定的延迟时间），时变电阻接入电路，电阻的时变特性通过设定好的多个时间点的电阻值模拟。压控时变电阻的参数一栏中最多可手动输入31个时间点的电阻值，所以燃弧期间用R21、R22、R23、R244个时变电阻；而熄弧阶段也分为R31、R322个时变电阻。基于压控时变电阻的电弧模型如图1所示。

图1 基于压控时变电阻的电弧模型的电路实现Fig. 1 Circuit implementation of the arc model based on voltage-controlled time-dependent resistance

结果表明，当电阻R（t）的V-flash设为≥8 166 V的某值时，电弧电压、电弧电流、电弧电阻分别如图2（a）—图2（c）所示。

图2 基于压控时变电阻电弧模型的仿真结果Fig. 2 The simulation results of the arc model based on voltage-controlled time-dependent resistance

由图2（a）、图2（b）、图2（c）各个波形中除了起弧阶段的趋势基本符合，其余阶段的波形变化基本不符。主要原因在于7个电弧电阻R（t）之间的独立性，除了R（t）之外无法同时控制其余R（t）是否投入以及投入时间；如果均进行手动控制，该模型将没有多大价值。基于压控时变电阻的电弧模型存在一些不足：

1）各个阶段的持续时间需要固定下来，这与实际中电弧特性略有差别。

2）3个阶段的电阻值通过手动输入，是事先选好的，不符合实际电弧电阻的随机性。

3）无法进一步模拟电弧电阻未被击穿时的情况，即当电阻击穿电压值较大时，由于压控时变电阻本身的功能有限，仿真结果不符合电阻模型的实际设想。

为了克服这些缺点，提出了基于TACS控制开关的电弧模型，该模型在电弧3个阶段的持续时间及各段电弧电阻方面都体现出了明显的随机动态变化，且对于击穿电压门限的限制更加灵敏。

2.2 基于TACS开关击穿电弧模型的总体设计

为了改进基于压控时变电阻的电弧模型的一些不足，首先做出如图3所示的总体模块设计。

图3 总体设计框图Fig. 3 The overall design diagram

2.3 模型完善与验证

在搭建各部分仿真线路之前，首先需对该模型作进一步完善，即对燃弧阶段的电弧电阻进行指数函数的拟合，求k值的取值范围；然后结合t2及（t2－t1）将已经拟合得到的函数与对应的离散数组进行对比，验证其准确性。

该部分的讨论主要用matlab来实现，基于对拟合函数的了解，要解决的问题归结如下：

确定拟合函数的类型为指数函数且形式基本为：

式中：k值待求；a、b主要进行 验证。

分析可得，a值约在0.001 2（即t2），b值确定0.000 8～0.001 6之间，对应t2－t1（待验证）。这可以作为确定参数初始值的依据。

基于这些数据，取k的平均值为11.083 6作为模型中k的值。所以确定燃弧阶段电阻表达式为：

同时，a值与t2（取0.001-0.001 9）、b值与（t2－t1）（取0.000 8-0.001 6）对应，也都得到了验证。

图4 拟合曲线与原始数据Fig. 4 Fitting curve with the raw data

2.4 运行结果分析归纳

通过设置门限值的大小来控制过电压即表示是否会产生电弧。由于本文的门限值是从系统中测取电压来的，所以当门限值超出系统最大幅值时，不会发生击穿过程，而在最大幅值之内，会在击穿时刻产生电弧。

图5 基于TACS开关电弧模型的仿真结果Fig. 5 The simulation results of the arc model based onof TACS switch

由图5可看出，当电压达到了击穿电压门限值，电弧过程将完整进行，而电压峰值未达到击穿电压门限值时，不存在电弧现象，只存在电压的一些波动。

对比随机运行3次中电弧各阶段的持续时间，如表1所示，表中三段持续时间均符合模型中描述的各阶段持续时间的范围，且具有随机性，克服了基于压控时变电阻的电弧模型的局限，使得改进的模型更具代表性。

表1 电弧各阶段的持续时间Tab. 1 Every stage of the arc duration

综合的运行结果得出结论：与基于压控时变电阻的电弧模型相比较，三段式电弧电阻模型更符合设想中的效果，更接近实际电弧模型的随机性和变化趋势，克服了之前模型中确定电弧击穿时刻的局限性，可以通过仿真得出电缆不同程度击穿情况下的电弧情形。

3 改进后的模型仿真结果

当电源初相角为-90°时电压到达击穿电压门限值就会有一段时间间隔，导致电弧电阻的数学模型带有一定的误差，影响电阻电弧模型的精确度。本文采取将击穿时刻提取出来，然后在电阻电弧的第二阶段中相应的减去未被击穿时刻的计数值，得到更加准确的计数时刻，从而提高了电阻电弧模型的精确度。最终仿真图如图6所示。方框所标为添加的提取击穿瞬间时刻。

当电源初相角为-90°时，将击穿电压设置为6 000 V，采取2种方式进行仿真，其结果如图7所示。

对比图7（a）、图7（b）、图7（c），在外界其他条件相同时，添加提取击穿时刻的方法能够更加准确地得到电阻电弧的模型，符合实际电弧情况。

4 结语

1）基于电弧模型的纯电阻特性，建立三段式击穿电弧模型，对三段电弧电阻数值具体量化。规范化改进后的模型更接近实际电弧模型的随机性和变化趋势，仿真得出电缆不同程度击穿情况下的电弧情形更加全面。

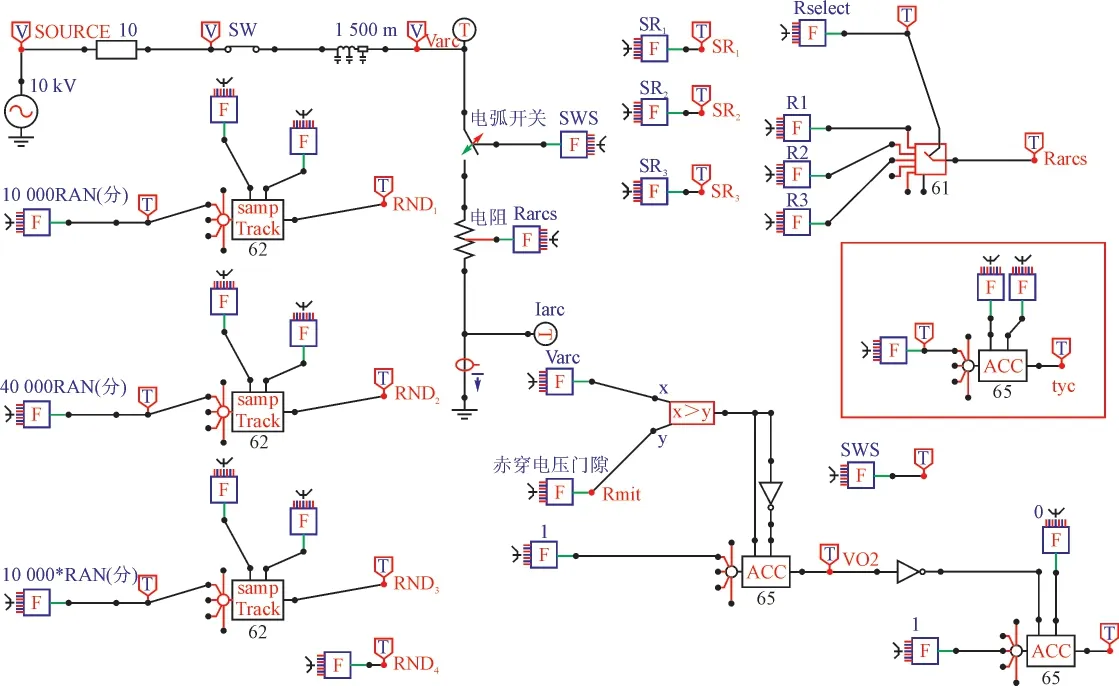
图6 改进后的电弧模型仿真图Fig. 6 The improved arc model simulation diagram

图7 对比仿真结果Fig. 7 Comparing the simulation results

2）针对该模型对电压门限的局限性采取了提取击穿瞬时时刻模块的方式来提高电弧模型的精确度，能够更好地体现电弧的动态特性。

3）对于本文中建立的电弧模型，其仿真结果与文献中的具体线路测量数据基本吻合，验证了该模型的正确性。由于故障电弧现象比较复杂，而该模型只是基于理论层面的一个研究成果，所以下一步应该更加深入地了解电缆模型以及故障测距机理。

[1] 许珉，白春涛，秦毅男，等. 电力电缆故障低压脉冲自动测距方法[J]. 继电器，2007，35（7）: 37-40.XU Min，BAI Chuntao，QIN Yinan. Method of power cable fault automatic location based on low voltage pulse[J].Relay，2007，35（7）: 37-40（in Chinese）.

[2] 王仁甫. 电弧现象模型的发展[J]. 高压电器，1991，27（4）: 39-46.WANG Renfu. The development of the phenomenon of arc model[J]. High Voltage Apparatus，1991，27（4）: 39-46（in Chinese）.

[3] 陈俊，谢林涛，钟杰，等. 重燃过电压下基于Mayr-Cassie 模型的电弧仿真分析[J]. 智能电网，2013（3）:106.CHEN Jun，XIE Lintao，ZHONG Jie，et al.Simulation of arc based on mayr-cassie model under restrike overvoltage[J].Smart Grid，2013（3）: 106（in Chinese）.

[4] GUARDADO J L，MAXIMOV S G，MELGOZA E，et al.An improved arc model before current zero based on the combined mayr and cassie arc models[J]. Power Delivery，IEEE Transactions on，2005，20（1）: 138-142.

[5] 薛小光，朱庆兰，刘红利. 电力电缆故障探测技术分析[J]. 电线电缆，2008（4）: 35-37.XUE Xiaoguang，ZHU Qinglan，LIU Hongli. Analysis of the technique f or power cable fault location[J]. Electric Wire & Cable，2008（4）: 35-37（in Chinese）.

[6] 许东升，田凤兰，赵珩，等. 电力电缆故障现场测距方法的研究与应用[J]. 高压电器，2009，45（5）: 136-140.XU Dongsheng，TIAN Fenglan，ZHAO Heng，et al.Research and application of power cable fault diagnostic method[J]. High Voltage Apparatus，2009，45（5）: 136-140（in Chinese）.

[7] 任艳霞，刘明光，史雪明. 电力电缆故障探测方法探讨[J]. 电力科学与工程，2008，24（1）: 30-33.REN Yanxia，LIU Mingguang，SHI Xueming. Survey of power cable fault detection methods[J]. Electric Power Science and Engineering，2008，24（1）: 30-33（in Chinese）.

[8] 李峰，徐丙垠. 电弧反射电缆故障测距装置脉冲发射时刻选择算法[J]. 电力系统自动化，2011（13）: 88-91.LI Feng，XU Bingyin. Reflex arc pulse firing moment cable fault location device selection algorithm[J]. Automation of Electric Power Systems，2011（13）: 88-91（in Chinese）.

[9] 李峰，徐丙垠，宫士营. 基于EMD的电弧反射电缆故障测距脉冲信号提取方法[J]. 电力系统自动化，2012（11）:92-96.LI Feng，XU Bingyin，GONG Shiying. Based on the EMD reflex arc of cable fault location pulse signal extraction method[J]. Automation of Electric Power Systems，2012，（11）: 92-96（in Chinese）.