基于IFA-ELM的航空发动机自适应PID控制新方法

焦洋，李秋红，李业波

(南京航空航天大学 能源与动力学院，江苏省航空动力系统重点实验室，南京210016)

民用大涵道比涡扇发动机控制通常采用燃油-转速闭环控制方式.目前国内外普遍采用PID方法对大涵道比发动机进行控制［1-2］.虽然PID控制具有一定的鲁棒性，且结构简单、易于工程实现，但由于航空发动机是时变的非线性系统，在全包线内，其参数及特性变化很大，所以单一的PID参数对发动机的全状态控制很难取得令人满意的效果，因而通常通过在包线范围内设置多组PID参数来使其适应发动机的不同工作状态.而这些PID参数只是针对发动机的某些稳态工作点设定的，不能很好地兼顾发动机的各自动态工作过程，影响系统响应的快速性，且存在控制器之间的切换问题，而切换易造成系统的不稳定，对于发动机控制来说是极为不利的.

针对这一问题，自适应PID控制提供了一种有效的解决方法.采用自适应PID控制可以自动根据发动机工作状态调节控制系统参数，使之与变化的工作状态相适应.因而在航空发动机控制领域，自适应PID控制得到了广泛的关注［3-5］.已有学者将智能映射网络和PID控制相结合，来提高控制系统对发动机参数变化的适应能力，从而提高控制系统的性能.本文借鉴这种设计思想，提出一种新颖的群智能优化算法与智能自适应PID相结合的控制方法.采用具有较快训练速度的极端学习机(ELM，Extreme Learning Machine)［6-8］对发动机下一步输出转速进行预测.由于ELM的输入层至隐含层权值和偏置随机产生，不适宜的随机值会影响估计的精度.为提高预测模型精度，减小网络计算规模，提出一种改进的萤火虫算法(IFA，Improved Firefly Algorithm)，用于优化ELM的初始权值，形成IFA-ELM算法，构建了基于IFA-ELM网络参数的民用涡扇发动机自适应PID控制器，在飞行包线内的各种工作状态间，能够自动调整控制器参数，获得稳定快速的响应.

1 IFA-ELM算法

近几十年发展起来的仿生模拟进化算法具有操作简单、可并行处理、鲁棒性强等特点［9-10］.其中，萤火虫算法(FA，Firefly Algorithm)由模拟自然界中萤火虫成虫发光的生物学特性发展而来，也是基于群体搜索的随机优化算法.该算法由剑桥学者Yang［11-12］提出，适用于解决多峰值优化问题.在基于极端学习机的发动机输出预测训练过程中，极端学习机的隐含层权值和偏置与预测效果之间并不具有单调性，因此采用萤火虫算法来对其进行优化.

1.1 改进的萤火虫算法

萤火虫算法是通过模拟萤火虫的群体行为构造出的随机优化算法，其仿生原理为:用搜索空间中的点模拟自然界中的萤火虫个体，将最优目标值的搜索过程模拟成萤火虫个体移动的过程.

萤火虫算法主要包含两个决定要素，即亮度和吸引度.亮度体现了萤火虫所处位置的优劣，并通过判断亮度大小决定其移动方向;吸引度决定了萤火虫移动的距离，通过亮度和吸引度的不断更新，实现目标优化.

萤火虫间的相对亮度和吸引度描述为

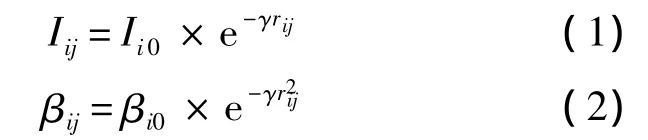
其中，Iij为萤火虫i相对萤火虫j的荧光亮度;Ii0为萤火虫i的最大萤光亮度，即自身(空间距离r=0处)荧光亮度;γ为光强吸收系数;rij为萤火虫i与j之间的空间距离;βij为萤火虫i对萤火虫j的吸引度;βi0为萤火虫i的最大吸引度.个体的最大萤光亮度与适应度值相关，适应度值越优，则自身最大荧光亮度越高.

基于相对荧光亮度的排序和比较，确定萤火虫的移动方向;根据吸引度计算，确定萤火虫的移动距离:

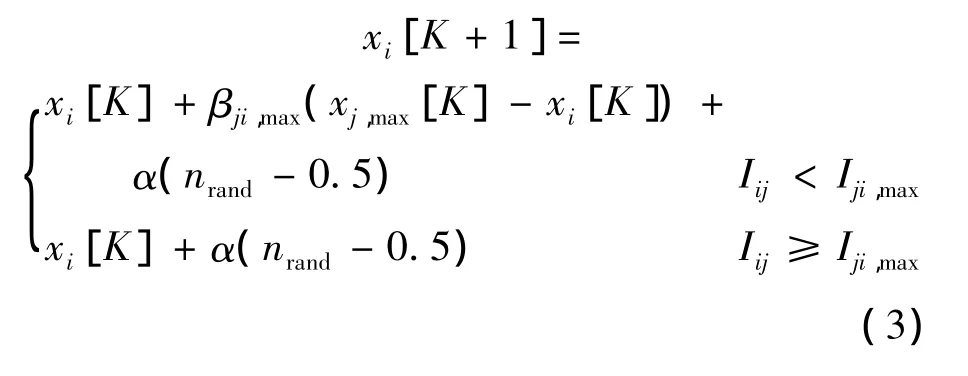
其中，［K］为xi的优化代数;α为随机扰动的缩放因子;Iji，max为群体中对萤火虫i相对荧光亮度最大的个体;xj，max为其位置;βji，max为其对萤火虫 i的吸引度;nrand为［0，1］上服从均匀分布的随机因子.

对于FA来说，光强吸收系数γ和缩放因子α是主要的控制参数.较大的α值使得算法具有较强的全局搜索能力，较小的α值使得算法具有较强的局部寻优能力.为平衡算法在前、后期的寻优策略，将常规FA中的固定缩放因子α进行改进，形成IFA.此时，缩放因子α不再为常数，而是通过式(4)根据进化代数调整:

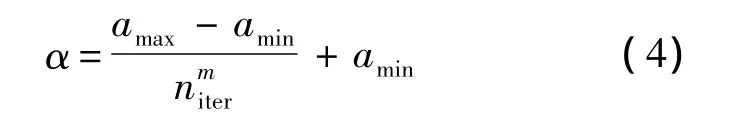
其中，amax和amin为缩放因子的上下限;niter为种群进化迭代次数;m为缩放因子α的调整系数，是在［0，1］之间的常数，调整系数m可反映缩放因子α的变化速度.

具体优化步骤如下:

1)生成初始种群.先将萤火虫群体随机散布在预定的解空间，每一只萤火虫因为所处位置不同且适应度值不同，造成的荧光亮度也不同.

2)选择萤火虫可能的移动方向.通过式(1)计算萤火虫间的相对荧光亮度，通过排序计算出对第i个萤火虫相对亮度最高的个体，相对荧光亮度高的萤火虫可以吸引第i个萤火虫向自己的位置移动.

3)确定移动后的位置.可能移动的方向确定后，根据式(3)和式(4)，通过相对荧光亮度的对比，确定是向相对荧光亮度最高的个体移动还是在原来的位置小范围内扰动，得到更新后的位置.

4)判断是否达到收敛条件.收敛则结束算法，否则回到步骤2).

这样经过多代进化后，所有萤火虫个体都将聚集在其搜索范围内亮度最高的萤火虫的附近位置上，从而实现寻优.

1.2 函数优化能力测试

选取3种常见的智能优化算法的测试函数.测试函数如下:

1)Eggcrate Functions:

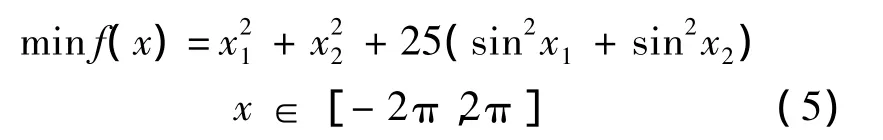
2)Six hump Camel Back:

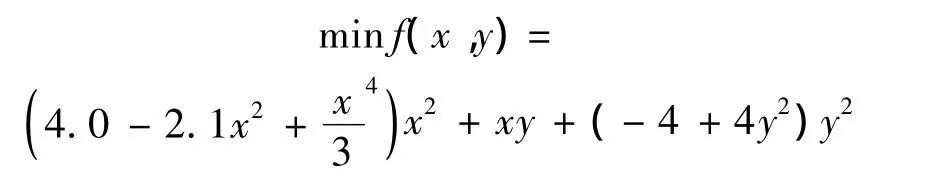
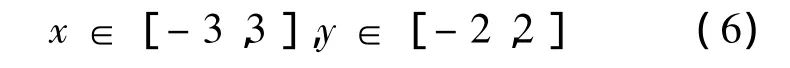
3)Schaffer Functions:

参数设置以及优化结果如表1所示.其中，缩放因子调整系数m=0.5，每种算法独立运行50次.从表中数据不难发现，在不同缩放因子的情况下，相较于FA，IFA均有较好的寻优结果.针对Eggcrate这样的典型多峰函数，初期较大的缩放因子有利于跳出局部，但是后期对最优解的收敛精度有不利影响;反之，对于Schaffer函数，虽然较小的初始缩放因子可以增加最优解的收敛精度，但是容易陷入局部最优.综上，即可体现出在提出的IFA算法改进中变缩放因子的优越性.Six hump Camel Back函数结构相对扁平，IFA依然可以取得较好的精度，更加全面地验证了其有效性.

表1 函数测试结果Table1 Function test results

1.3 基于IFA的ELM改进

在ELM算法中，给定一个训练数据集χ={x，t}N，针对第 i组训练数据有 χi={xi，ti}N，其中输入数据 xi=［xi1，xi2，…，xin］∈Rn，期望输出数据 ti=［ti1，ti2，…，tis］T∈Rs，输入层节点数为n，输出层节点数为 s并设隐含层激励函数为f(x).

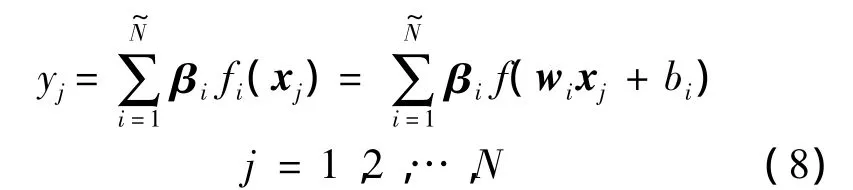
其中，wi=［wi1，wi2，…，win］T为连接隐含层节点 i与输入层节点的权值;bi为隐含层节点i的偏置;βi=［βi1，βi2，…，βis］T是连接隐含层节点 i和输出层节点的权值.

对于第i个隐含层节点，其输出为

结合式(8)和式(9)，可以得ELM的学习过程为

4.1.1 以护理项目为评价对象 护理项目是质量评价的基本单元，传统的护理质量评价主要将护理项目作为评价对象，如特护、1级护理质量、护理技术操作合格率、健康教育的实施效果等。

其中

H为隐含层矩阵;t为期望输出矩阵.

输出权值β可由下式求得:

其中H+为ELM网络输出层矩阵H的广义逆.

由于ELM的输入层权值是随机给定的，在获得相同训练精度的条件下，需要的隐含层节点数较多，而为了追求较高的预测精度往往会使网络结构变得复杂.

除此之外，复杂的映射网络结构会相对占用更多的系统资源，增加系统的响应时间，不利于PID参数的动态调整.为了减少隐含层节点的数目，提高ELM算法的稳定性和精度，利用IFA算法优化ELM的输入层至隐含层的权值和偏置，形成IFA-ELM算法，其流程如下:

1)初始化IFA算法基本参数.设置萤火最大吸引度β0，光强吸收系数γ，缩放因子界限αmax，αmin，缩放因子调整系数 m，最大迭代次数 niter，max，萤火虫种群规模nv.将适应度值定义为R(·).通过下式计算适应度值:

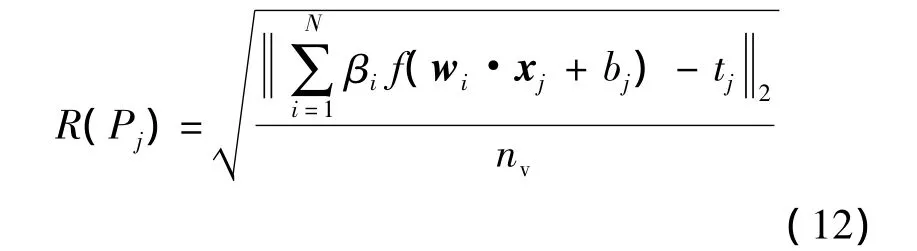
其中，Pj为萤火虫个体;βi为输出层权值;f为隐含层函数;tj为期望输出.

2)计算萤火虫的适应度值作为各自最大萤光亮度I0，形成初代萤火虫种群P.

3)针对种群中的每个个体Pi，利用式(11)计算对应的输出层矩阵β.

4)根据相对荧光亮度和吸引度决定萤火虫的移动方向和位置.

5)根据更新后萤火虫的位置，计算适应度，更新最优个体Pbest，并根据适应度值更新种群个体最大荧光亮度，其中 Ibest0为当代最优个体最大荧光亮度.

6)检查是否满足终止条件，即最大迭代次数，若满足则结束，否则转步骤3)继续，迭代计算直到最大迭代次数 niter，max.

7)将最优萤火虫个体Pbest的结果作为最优输入层到隐含层的权值和偏置进行输出.

1.4 IFA-ELM算法仿真测试

为验证IFA-ELM算法的优化有效程度，将IFA-ELM算法与标准的ELM算法在3个Benchmark回归数据集上进行了测试，假设萤火最大吸引度β0=1，光强吸收系数γ=0.2，缩放因子界限αmax=0.6，αmin=0.01，缩放因子调整系数 m=0.5，最大迭代次数 niter，max=50，萤火虫种群规模nv=100.结果如表2所示.表中数据为30次运行结果的平均值，测试环境的 CPU为 I3-M330(1.8 GHz)，内存为 4 G.

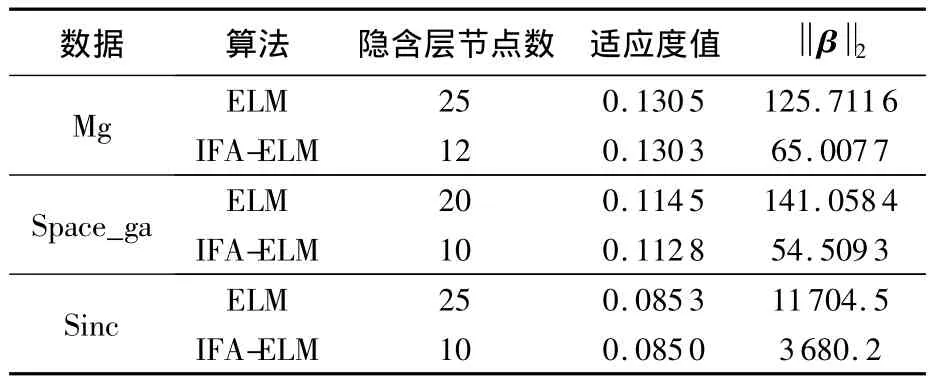
表2 Benchmark回归数据测试结果Table2 Test results of Benchmark data for regression

与ELM相比，IFA-ELM算法在达到相同的测试精度的情况下，其隐含层节点个数要远少于ELM算法.这就大大降低了网络的复杂性，从而减少了算法预测时间，提高了其在线使用的实时性.此外，IFA-ELM的输出层权值的范数均小于ELM，这说明IFA-ELM具有更好的泛化能力.

2 基于IFA-ELM的自适应控制

2.1 预测模型

设计的航空发动机预测控制系统是通过IFA-ELM智能映射方法对发动机被控变量变化进行预测的.在训练过程中，需充分利用当前信息及历史信息，最终准确预测出模型被控量的输出，这是预测控制的核心思想［14］.

在ELM设计过程中，将发动机前一时刻的被控变量输出、当前时刻的控制量输入及被控变量输出作为网络的输入，对发动机在下一时刻的被控变量输出进行预测，依据预测输出对输入的变化率调节PID参数.以某型民用航空发动机非线性模型为例进行预测PID控制器的设计控制系统具有如图1所示的结构.

图1 自适应PID控制系统闭环结构图Fig.1 Adaptive PID closed-loop control system diagram

模型中，输入量为燃油流量Wf，输出量为风扇转速nL.因此，选择预测网络输入向量r=［r1，r2，r3］T=［nL(k－1)，nL(k)，Wf(k)］T，其中 k为步数，隐层选8个神经元，输出为下一步风扇转速预测n^L(k+1).f为隐含层激励函数，此处选为logsig，即

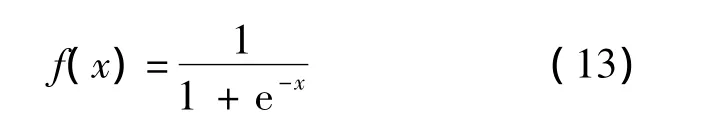
采用线性输出节点，则网络输出为系统实际输出的预测值.

其中，βj为输出层权值;hj为隐含层输出.

利用IFA-ELM网络辨识输出近似代替发动机的实际输出.

2.2 基于模型预测的自适应PID控制

离散化后的增量式航空发动机PID控制算法可表示为

其中

e(k)，e(k－1)和e(k－2)分别为系统当前误差、前1步误差及前2步误差;r为转速指令信号;Kp，Ki和Kd分别为比例系数、积分系数和微分系数.

自适应PID控制器性能指标为

采用梯度下降法［15］调整 Kp，Ki和 Kd，可得Kp参数的自整定公式为

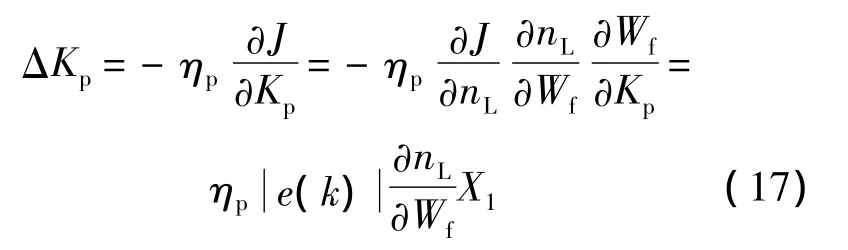
其中，ηp为比例梯度下降系数;∂nL/∂Wf由IFA-ELM网络辨识参数，结合式(9)和式(14)，可得

其中

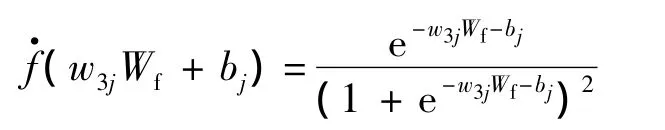
ΔKi和ΔKd的自整定公式与ΔKp类似，所以不再给出.可见，该算法实现了基于发动机输出预测网络的控制器参数调整.

3 自适应PID控制仿真

在飞行包线内对某通用大涵道比涡扇发动机模型进行了采样，在飞行高度为10 km内的情况下，通过变化高度和马赫数，在推拉油门杆位置采集了4604组动态数据.对采样所得的数据归一化，选其中的2/3作为训练数据，其余作为测试数据.借助Matlab分别采用常规ELM、BP神经网络以及IFA-ELM这3种算法进行网络训练和测试，隐含层节点数均选为8个，结果如图2和图3所示.可见IFA-ELM网络能够很好地预测发动机的输出，并且精度相较于前两种智能映射网络有明显提高.

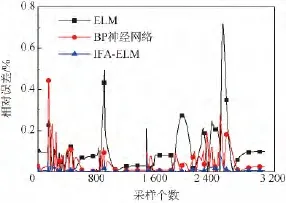
图2 训练数据相对误差Fig.2 Training data relative error

图3 测试数据相对误差Fig.3 Testing data relative error

将所训练的IFA-ELM网络用于PID控制参数的调整，开展基于IFA-ELM网络的自适应PID控制的仿真验证，以选择2个工作点为例:①在地面点:高度H=0 km，马赫数为0，油门角度从20°推到70°再回到20°的大动态仿真模拟;②常规民机巡航点:高度H=10 km，马赫数为0.8，油门角度从50°推到70°再回到50°的中等过渡状态仿真模拟.经调试，初始PID参数分别为地面点:Kd=0.1，Ki=0.1，Kp=3;常规民机巡航点:Kd=0.1，Ki=0.3，Kp=5.

图4为H=0 km时的PID参数整定曲线，可见伴随着发动机工作状态的变化，PID参数发生较大的调整，实现了PID参数的在线自适应整定.

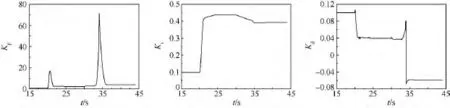
图4 H=0 km时的PID参数整定曲线Fig.4 PID parameter tuning curves when H=0 km

图5给出了被控制量nL、燃油流量Wf、压气机出口总压P3、涡轮前总温T4以及余气系数αk的响应曲线.由图可见，系统工作在安全限制范围内，与常规PID控制相比，自适应PID控制具有更快的响应速度.为了清晰显示两种控制算法的差异，图5中同时给出了nL响应曲线的两点放大图.A点在初始加速阶段，B点在减速终止阶段.加速起始阶段，常规PID控制存在较为明显的滞后;自适应PID控制通过在线快速调整控制器参数输出，能快速、准确跟踪指令信号.在减速终止阶段，常规PID控制有较大超调，调节时间较长，自适应 PID超调量减少1.5%，调节时间缩短1.4 s(按±2%误差带计算)，验证了在大的动态过程中自适应PID控制的优越性.

图6和图7给出了中等过渡状态下PID参数和发动机输出响应曲线.由图可见，PID参数同样发生了较大范围的调整，其他参数也都在安全范围之内.图7中同样给出了nL响应曲线的两点放大图，都是在接近稳态处的响应对比，与常规PID控制相比，自适应PID控制在超调量和调节时间上具有明显的优势，超调量至少减小0.2%，调节时间至少缩短0.2 s.

图5 H=0 km时的发动机响应曲线Fig.5 Engine response curves when H=0 km

图6 H=10 km时的PID整定曲线Fig.6 PID parameter tuning curves when H=10 km

图7 H=10 km时的发动机响应曲线Fig.7 Engine response curves when H=10 km

4 结论

本文提出一种IFA-ELM优化算法，将改进的萤火虫算法用于优化ELM输入层至隐含层的权值和偏置，可在保证ELM预测精度的前提下减小网络的规模，增强其泛化能力，提高控制系统的实时性.基于某型民用涡扇发动机，利用IFA-ELM算法设计了模型预测PID控制.相较常规PID控制，自适应PID控制能够根据发动机动态性能变化在线调整PID参数，从而提高控制系统对对象参数变化的适应能力，进一步提高控制系统的性能.该算法从一组PID控制参数开始，利用一组离线训练的极端学习机网络参数，可实现全包线范围内的发动机各种工作状态控制，具有良好的实时性，与需要在包线内通过高度、马赫数、油门角度差值的常规发动机PID控制相比，占用的存储空间更小，计算过程更简便，动态控制性能更好.

References)

［1］ Milhim A B.Modeling and fault tolerant PID control of a quadrotor UAV［D］.Montreal:Concordia University，2010.

［2］ 殷锴，陶金伟，王鸿钧，等.民用航空发动机控制系统回路设计与仿真［J］.航空计算技术，2013，42(6):107-110.Yin K，Tao J W，Wang H J，et al.Closed-loop design and simulation of civil aero-engine control system［J］.Aeronautical Computing Technique，2013，42(6):107-110(in Chinese).

［3］ 乔伯真，缑林峰.模糊自整定PID的航空发动机转速控制研究［J］.计算机仿真，2013(4):63-67.Qiao B Z，Hou L F.Rotating speed control for aero-engine based on fuzzy self-tuning PID controller［J］.Computer Simulation，2013(4):63-67(in Chinese).

［4］ 李述清，张胜修，刘毅男.航空发动机全包线最优PID控制器设计［J］.弹箭与制导学报，2011，31(4):105-107.Li S Q，Zhang X S，Liu Y N.Neural network based on optimal PID controller over whole envelope for an aero-engine［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2011，31(4):105-107(in Chinese).

［5］ 赵俊，陈建军，王灵刚.航空发动机的智能神经网络自适应控制研究［J］.航空动力学报，2008，23(10):1913-1920.Zhao J，Chen J J，Wang L G.New intelligent neural network adaptive control scheme research for aero-engine［J］.Journal of Aerospace Power，2008，23(10):1913-1920(in Chinese).

［6］ Huang G B，Ding X，Zhou H.Optimization method based extreme learning machine for classification［J］.Neurocomputing，2010，74(1):155-163.

［7］ Suresh S，Saraswathi S，Sundararajan N.Performance enhancement of extreme learning machine for multi-category sparse data classification problems［J］.Engineering Applications of Artificial Intelligence，2010，23(7):1149-1157.

［8］ Liu N，Wang H.Ensemble based extreme learning machine［J］.IEEE Signal Processing Letters，2010，17(8):754-757.

［9］ 李雪梅，张素琴.基于仿生理论的几种优化算法综述［J］.计算机应用研究，2009，26(6):2032-2034.Li X M，Zhang S Q.Overview of some optimization algorithm based on bionic theory［J］.Application Research of Computers，2009，26(6):2032-2034(in Chinese).

［10］ Zang H，Zhang S，Hapeshi K.A review of nature-inspired algorithms［J］.Journal of Bionic Engineering，2010，7(Supplement):S232-S237.

［11］ Yang X S.Nature-inspired metaheuristic algorithms［M］.Beckington:Luniver Press，2010:81-89.

［12］ Yang X S.Firefly algorithms for multimodal optimization［M］.Heidelberg，Berlin:Springer，2009:169-178.

［13］ Silva D N G，Pacifico L D S，Ludermir T B.An evolutionary extreme learning machine based on group search optimization［C］//Proceeding of 2011 IEEE Congress on Evolutionary Computation.Paris:IEEE，2011:574-580.

［14］ Richter H，Singaraju A V，Litt J S.Multiplexed predictive control of a large commercial turbofan engine［J］.Journal of Guidance，Control，and Dynamics，2008，31(2):273-281.

［15］ 李秋红，许光华，孙健国.航空发动机小波神经网络PID控制［J］.航空动力学报，2009，24(4):875-879.Li Q H，Xu G H，Sun J G.Aero-engine wavelet neural network PID control［J］.Journal of Aerospace Power，2009，24(4):875-879(in Chinese).