箱式动力结构的振动传递特性分析

高维金，王亮，刘永光

(北京航空航天大学 自动化科学与电气工程学院，北京100191)

在节能减材和领域特殊需求的背景下，多领域的装备朝着大型化、高速化、轻量化的方向发展，其装备构件呈现出了柔性大、结构阻尼小的特点.对于本身内部含有动力源的箱式动力结构，如舰船减速器、风电齿轮箱及直升机齿轮箱［1］等，在实际工作过程中，由于工况的频繁改变，柔性较大的构件可能产生振动，甚至损坏.为了能有效地抑制结构振动，进行如结构动力学优化［2］、基于磁致伸缩作动器的主动控制［3-7］等，需要对箱式动力结构振动传递机理进行研究.文献［8-11］建立齿轮轴-轴承-箱体的完整有限元模型，并赋予初始边界条件进行有限元仿真，分析系统的动力学传递特性.此外，则是通过集中质量法对啮合齿轮副建立质量-弹簧-阻尼的数学模型，采用传递矩阵法计算得到箱体的轴承座处的动载荷，以此作为有限元箱体模型的激励条件，研究箱体的振动特性［12-14］.从文献来看，有限元法和集总模型传递矩阵法是主要的研究方法.相比而言，有限元法计算精度较高且可以避免传递矩阵法中可能出现的数值不稳定现象［15］.

因此，考虑齿轮啮合错位、齿侧间隙等因素建立减速器的三维传动模型，采用Craig-Bampton缩减法将箱体缩聚为6个轴承孔中心处节点的柔性体，分析啮合副的啮合时变刚度、啮合线性传递误差及轴向重合度.在此基础上，从输入轴扭矩波动和线性传递误差分别为激励条件的两方面，对传动系统基于轴段节点的思想进行了计算，得到箱体轴承处的加速度频率关系，为后续的箱体优化及基于超磁致伸缩作动器的主动振动控制提供了边界条件及相关数据.

1 研究对象及模型

1.1 研究对象

图1为某二级减速箱的传动机制，Z1和Z2分别为安装在输入轴和中间轴上的主、从动斜齿轮，Z3和Z4分别为安装在中间轴和输出轴上的主、从动直齿轮.各啮合副的相关参数见表1.

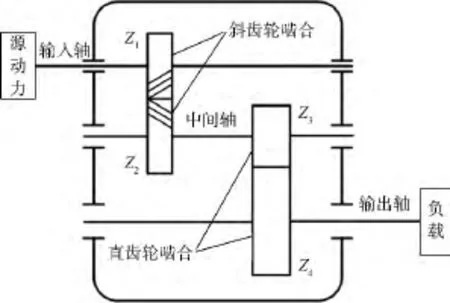
图1 某二级减速箱的传动机制Fig.1 Transmission mechanism of two-stage reducer

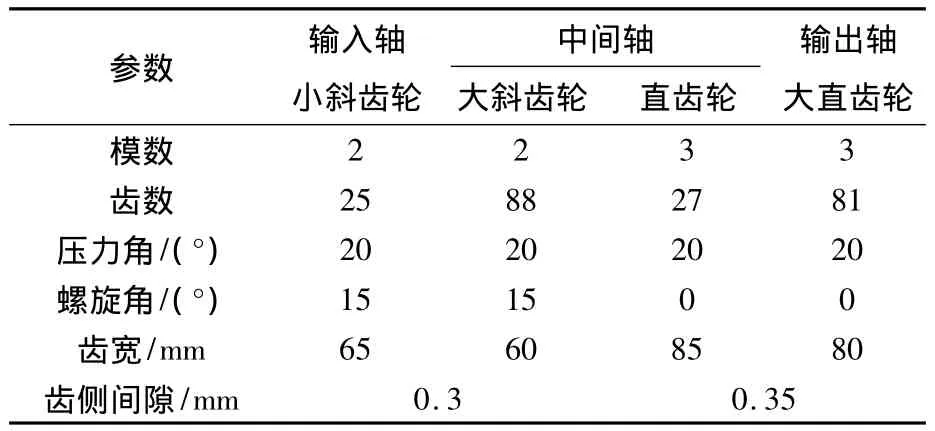
表1 啮合齿轮的基本参数Table1 Basic parameters of meshing gear

1.2 研究模型

为了研究箱体的振动特性以及箱体的柔性变形对传动的影响，将箱体作柔性化处理.从提高计算效率及所关心的个别节点变形或响应的角度来看，需要根据实际情况将模型缩聚到所要求解的自由度.在减速箱系统中箱体视为子结构，采用Craig-Bampton［16］子结构固定界面模态综合法将箱体的弹性变形用模态坐标的形式表达出来.Craig-Bampton子结构固定界面模态法可描述为

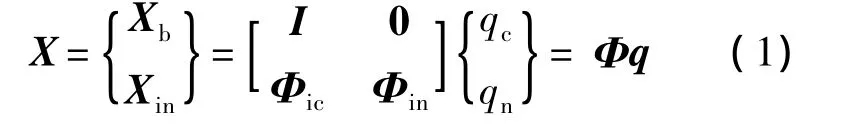
式中，Xb和Xin分别为界面节点与内部自由度的位移;Φic为界面坐标依次产生单位位移引起的内部静模态;Φin为固定界面分支正则化主模态;qc为约束模态的坐标;qn为固定界面正则化模态坐标.

为了能够反映边界作用效应及高阶模态，引入正则模态N，则原有模态坐标可以表述为

式中q*为Craig-Bampton模态坐标

将式(2)代入式(1)中可得

式中Φ*为具有原系统主模态和约束模态所有特性的正交Craig-Bampton模态.

图2为箱体、齿轮、传动轴的三维模型.将箱体视为子结构，基于Craig-Bampton缩减法作柔性化处理，缩聚节点为6个轴承孔中心处，节点用于将来自齿轮传动的力传递到箱体.缩聚节点的编号见图3.

图2 减速箱的三维模型Fig.2 Three-dimensional model of reducer

图3 箱体缩聚节点编号Fig.3 Reduction nodes number of gearbox

2 箱式动力结构振动激励分析

2.1 齿轮啮合时变刚度

齿轮啮合刚度对于齿轮振动来说是一个很重要且复杂的参量，它是研究齿轮动态性能的基础.齿轮的啮合刚度受传递载荷、轮齿弹性变形、啮合位置等诸多因素影响，建立其啮合刚度模型是很复杂的问题.考虑二级减速箱的啮合错位因素，分析齿轮啮合时变刚度.啮合错位正负的定义如图4所示.在模型中，若错位是沿着局部坐标系z轴的正方向，其值为正(图4(a));若错位值沿着局部坐标系z轴的负方向，其值为负(图4(b)).通过轴、轴承的变形以及工作载荷状况计算的齿轮啮合错位如图5所示.

斜齿轮的法截面单位接触啮合刚度和端截面单位接触啮合刚度的关系为［17］

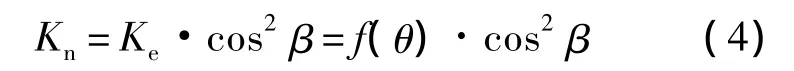
图4 啮合错位值正负的定义Fig.4 Definition of plus and minus symbol for meshing misalignment

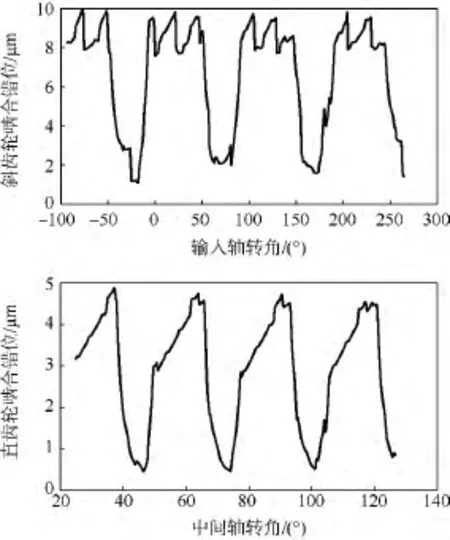
图5 斜齿轮和直齿轮的啮合错位Fig.5 Meshing misalignments of helical gears and spur gears

式中，Kn为法截面单位接触啮合刚度;Ke为端截面单位接触啮合刚度;β为斜齿轮螺旋角;f(θ)为端截面单位接触啮合刚度关于齿轮转角的函数.

斜齿轮单对齿啮合时变刚度的表达式为［18］

式中，K为斜齿轮副的啮合时变刚度;θ为输入轴的转角;W为斜齿的有效宽度;θm为输入轴斜齿轮的每齿平均转角;εa为轴向重合度;βb为基圆螺旋角;θ1和θ2为齿轮啮合接触线的最小和最大滚动角.

直齿轮的啮合时变刚度求解相对简单，只需将单位接触刚度乘以有效工作齿宽，再考虑重合度即可.

根据模拟计算可得，斜齿轮的轴向重合度最小为1.608，最大为1.739，可知斜齿轮的传动较为平稳.直齿轮的传动比最小为1，最大为2，齿轮单双对齿交替啮合，易造成冲击.

计及啮合错位的影响，运用齿轮啮合刚度的计算公式得到斜齿轮副和直齿轮副的单对齿啮合时变刚度，如图6所示.

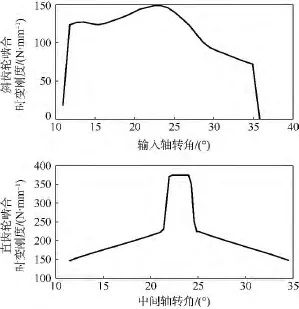
图6 斜齿轮和直齿轮的啮合时变刚度Fig.6 Time-varying meshing stiffness of helical gears and spur gears

2.2 齿轮啮合传递误差

在没有制造及安装误差且啮合刚度很大的理想情况下，系统可按固定的传动比进行工作，不存在传递误差.然而实际中齿轮的制造及装配误差、啮合错位、啮合时变刚度等因素导致齿轮在啮合线方向产生传递误差，进而这些误差对系统产生激励力［19-20］.传递误差(TE，Transmission Error)就是沿啮合线方向被动齿轮上的齿廓在实际啮合位置同理想条件下啮合位置的偏差，其波动直接反映了被动齿轮的不均匀性，对传动系统的振动及噪音有着重要影响.图7为传递误差示意，其中A为理论啮合位置，A′为主动轮转过一定角度与从动轮啮合位置.

设主动轮转角为θa，基圆半径为Rb1;从动轮转角为θp，基圆半径为Rb2.则沿啮合线方向的传递误差表达为

在考虑啮合错位、啮合时变刚度及齿侧间隙的情况下，斜齿轮副和直齿轮副间的传递误差如图8所示.

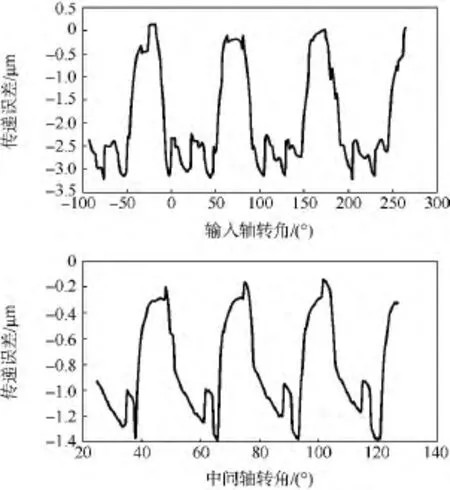
图8 斜齿轮副间和直齿轮副间的传递误差Fig.8 Transmission error of helical gears and spur gears

3 振动传递机理及振动评估

3.1 振动传递机理

在箱式动力结构系统中，往往会产生一些扰动因素，如传动齿轮的啮合冲击、错位滑动旋转不平衡等.由于这些因素的长期作用，系统中的某个部件就可能产生未变形，然后以弹性波的形式沿着系统装配连接的路径关系进行传递或者以固体噪声发射到周围环境［21］.当弹性波通过这些弹性部件(轴、齿轮、轴承及箱体)时，可能激发部件的自然频率发生共振，结果扰动振动加剧，形成恶性循环.图9为振动弹性波能量传递的示意图.图中实线表示振动的传递路径，虚线表示内部固体声辐射到箱体形成二次噪声.

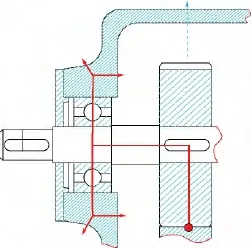
图9 振动传递示意图Fig.9 Schematic diagram of vibration transmission

3.2 不同激励的振动特性及振动评估

根据3.1节中的振动传递机理，从输入端扭矩波动及齿轮传动误差两方面来研究振动在系统中的传递特性.

3.2.1 齿轮传递误差激励的振动特性

由于齿轮啮合时变刚度具有明显的周期性，故可将传递误差以齿轮啮合频率进行傅里叶级数展开为

式中，Ta为平均传递误差;Ti为谐波幅值，i为谐波阶数;ω为齿轮啮合频率;Φi为谐波相角.

以斜齿轮啮合传递误差谐波为激励，基于节点的思想分析各轴段及缩聚节点处的响应.图10为传递误差的谐波幅值图，表2为相关的传递误差谐波数据.

图10 传递误差的谐波幅值Fig.10 Harmonic value of transmission error

输入轴、中间轴、输出轴的节点划分示意见图11.节点的划分是根据部件连接位置、轴肩位置确定的.输入轴的节点从左到右依次是Node1～Node12，中间轴的依次为Node1～Node9，输出轴的依次为Node1～Node11.

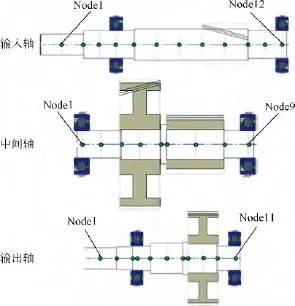
图11 各轴段的节点划分Fig.11 Node division of each shaft section

限于篇幅，仅给出传递误差一次谐波激励下轴段轴承处节点的响应，若进行后续的轴段优化，则需求取其他节点处的响应.输入轴的速度为1000 rad/min，输入功率为0.6 kW.考虑齿轮啮合传递误差激励，振动通过齿轮轴-轴承的路径传递给箱体.图12给出了输入轴、中间轴、输出轴箱体缩聚节点处在0～5 kHz频率范围内的加速度响应.

图12 缩聚节点处的加速度响应Fig.12 Accelerated speed response of reduction nodes

理想情况下，同一轴两侧轴承处的动态响应一致，这样系统运行比较平稳，不会产生额外的扰动，也便于振动的控制.从图12中可以看出，在0～1.5 kHz频段输入轴轴承的缩聚节点处动态特性几乎一致，1.5～4.5 kHz频段动态特性相差较大，4.5～5.0 kHz频段的动态特性几乎趋于一致.对于中间轴轴承处的缩聚节点，可以看出缩聚节点3和5的动态加速度响应在0～5kHz频段内几乎趋于一致.对于输出轴轴承处的缩聚节点4和6来说，在0～3 kHz频段内动态加速度响应趋势比较一致，3～5 kHz频段内，两节点的加速度响应不一致.

图13给出了输入、中间、输出轴三者轴承内外圈处的动态加速度响应.从图13中可以看出，输入轴和中间轴处的轴承内圈动响应经过滚动体传递到外圈时，缩聚节点动响应得到衰减，轴承起到了隔振的作用.而在输出轴轴承外圈处的响应在0～4 kHz频段内几乎没有被衰减，在4～5 kHz频段内才在一定程度上衰减，轴承没有起到隔振作用，可能的原因是轴承选择不当，承受载荷的能力不足.

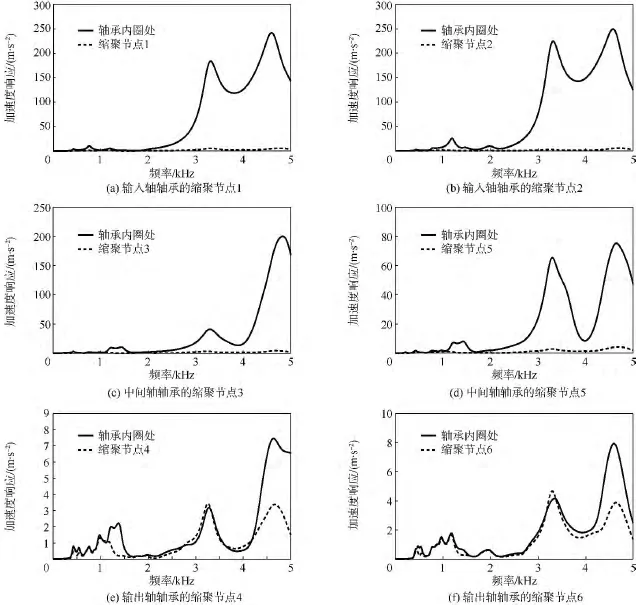
图13 输入、中间及输出轴轴承内外圈响应Fig.13 Dynamic response of inner and outer rings of the bearing at input shaft，middle shaft and output shaft

3.2.2 输入扭矩波动的振动特性

由于动力源的输出存在一定的转速波动，导致减速箱输入轴产生扭矩波动，使得非工作齿轮副中的齿轮不能及时和相应啮合的齿轮进行啮合，而是在与其啮合齿轮的两啮合面之间单面敲打或双面敲打，从而产生出齿轮的敲击噪声.图14给出了在输入轴扭矩波动的条件下，输入轴、中间轴、输出轴三者轴承处缩聚节点在频率0～10 kHz的动态加速度响应.

从图14中可以看出，输入轴扭矩波动的情况下，两轴承处的缩聚节点加速度响应在1 kHz和2kHz处有偏差，其余频段基本趋于一致.对于中间轴和输出轴，在0.8～4kHz频段内缩聚节点加速度响应有偏差，其余频段响应趋势基本一致.

图14 输入、中间及输出轴轴承处缩聚节点响应Fig.14 Response of reduction nodes of bearings at input shaft，middle shaft and output shaft

3.2.3 箱体振动评估

采用四面体单元划分箱体，单元划分如图15所示，单元总计为77 225个，节点数为22 940.单元材料为铸铁，弹性模量为1.68×105MPa，密度为7.1 ×103kg/m3，泊松比为0.27.箱体底部全部节点6个自由度约束，作为模型求解的边界条件.质量矩阵归一化处理，基于Block Lanzos方法提取箱体的前6阶固有频率如表3所示.

图15 箱体有限元模型Fig.15 Finite element model of gearbox

表3 箱体前6阶固有频率Table3 The first six natural frequencies of gearbox

对于啮合误差传递激励而言，箱体设计根据实际工况要求避开其共振频率点;对于输入轴扭矩波动激励来说，输入轴、中间轴、输出轴三者轴承处缩聚节点的加速度响应在8 kHz以后几乎趋于零，说明对于扭矩波动带来的振动能量在高频段以后经过齿轮-轴-轴承就已衰减了，而且该减速器箱体的最低固有频率为39.0392kHz，不可能引起共振，可见该减速器箱体设计保守，有进一步优化的空间.

4 结论

通过对减速箱三维建模，考虑啮合时变刚度、啮合错位等非线性因素，进行振动传递特性的分析，得出以下结论:

1)采用Craig-Bampton缩聚法将箱体进行缩聚作为柔性子结构，提高了计算效率，基于轴段节点思想计算得到缩聚节点处的动态响应，根据相关数据评估了箱体的振动特性，箱体设计保守，有进一步优化的空间.缩聚节点的动态响应为后续的箱体优化提供了激励条件.

2)由于结构模型所选参数不同，在文中所用方法基础上得到的轴承处响应与文献［19-20］中的结果不具有直接相比性，但数据变化的趋势一致，可以作为一种评估动力结构振动特性的方法.进一步的验证会在后续的试验研究中进行.

References)

［1］ Mucchi E，Vecchio A.Acoustical signature analysis of a helicopter cabin in steady-state and run up operational conditions［J］.Measurement，2010，43(2):283-293.

［2］ 顾松年，徐斌，荣见华，等.结构动力学设计优化方法的新进展［J］.机械强度，2005，27(2):156-162.Gu S N，Xu B，Rong J H，et al.Recent progresses on structural dynamic design methods［J］.Journal of Mechanical Strength，2005，27(2):156-162(in Chinese).

［3］ Yamamoto Y，Eda H，Shimizu J.Application of giant magnetostrictive materials to positioning actuators［C］//Advanced Intelligent Mechatronics Proceedings.Atlanta:IEEE，1999:215-220.

［4］ 柳萍，毛剑琴，张伟，等.基于Hammerstein-like模型的超磁致伸缩作动器建模与控制［J］.北京航空航天大学学报，2013，39(7):917-921.Liu P，Mao J Q，Zhang W，et al.Modeling and control of giant magnetostrictive actuators based on Hammerstein-like model［J］.Journal of Beijing University of Aeronautics and Astronautics，2013，39(7):917-921(in Chinese).

［5］ 郭咏新，毛剑琴.超磁致伸缩作动器的率相关建模与跟踪控制［J］.北京航空航天大学学报，2013，39(10):1360-1365.Guo Y X，Mao J Q.Rate-dependent modeling and tracking control of giant magnetostrictive actuators［J］.Journal of Beijing University of Aeronautics and Astronautics，2013，39(10):1360-1365(in Chinese).

［6］ 张旭辉，刘永光，付永领.一种新颖超磁致伸缩作动器的隔振模型［J］.北京航空航天大学学报，2007，33(11):1317-1320.Zhang X H，Liu Y G，Fu Y L.Novel model of active vibration isolation based on giant magnetostrictive actuator［J］.Journal of Beijing University ofAeronauticsand Astronautics，2007，33(11):1317-1320(in Chinese).

［7］ 李超，李琳.磁致伸缩材料作动器用于主动振动控制的实验研究［J］.航空动力学报，2003，18(1):134-139.Li C，Li L.Active vibration control using magnetostrictive material［J］.Journal of Aerospace Power，2003，18(1):134-139(in Chinese).

［8］ 余光伟.多平行轴齿轮-轴承-转子系统耦合振动的有限元分析［D］.上海:上海大学，1999.Yu G W.Analysis of coupling vibration of multi-stage gear-bearing-rotor systems with finite element method［D］.Shanghai:Shanghai University，1999(in Chinese).

［9］ Parker R G，Guo Y，Eritenel T，et al.Vibration propagation of gear dynamics in a gear-bearing-housing system using mathematical modeling and finite element analysis，NASA/CR-2012-217664［R］.Cleveland:NASA，2012.

［10］ Li R F，Yang C Y，Lin T J.Finite element simulation of the dynamical behavior of a speed-increase gearbox［J］.Journal of Materials Processing Technology，2004，150(1):170-174.

［11］ Rook T E.Mobility analysis of structure-borne noise power flow through bearing in gearbox-like structures［J］.Noise Control Engineering Journal，1996，44(2):69-77.

［12］ 吴文光.人字齿轮传动系统的建模及其动力学特性的有限元分析研究［D］.南京:南京航空航天大学，2010.Wu W G.Parametric modeling of herringbone gear drive system and finite element analysis of its dynamic characteristics［D］.Nanjing:Nanjing University of Aeronautics and Astronautics，2010(in Chinese).

［13］ Tordion G V，Gauvin R.Dynamic stability of a two-stage gear train under the influence of variable meshing stiffness［J］.ASME Journal of Engineering for Industry，1977，99(3):785-791.

［14］ 秦大同，杨军，周志刚，等.变载荷激励下风电行星齿轮系统动力学特性［J］.中国机械工程，2013，24(3):295-300.Qin D T，Yang J，Zhou Z G，et al.Dynamics characteristic of planetary gear system of wind turbines under varying load［J］.China Mechanical Engineering，2013，24(3):295-300(in Chinese).

［15］ 钟一谔，何衍宗，王正，等.转子动力学［M］.北京:清华大学出版社，1987:143-174.Zhong Y E，He Y Z，Wang Z，et al.Rotor dynamics［M］.Beijing:Tsinghua University Press，1987:143-174(in Chinese).

［16］ Craig R R，Bampton M C C.Coupling of substructures for dynamics analyses［J］.AIAA Journal，1968，6(7):1313-1319.

［17］ 唐增宝，钟毅芳，戴玉堂.斜齿圆柱齿轮传动的静态啮合刚度和动态啮合刚度［J］.机械设计，1993，10(6):10-13.Tang Z B，Zhong Y F，Dai Y T.Static meshing stiffness and dynamic meshing stiffness of helical cylindrical gear drive［J］.Journal of Machine Design，1993，10(6):10-13(in Chinese).

［18］ 彭国民，余波，马小英.动力总成NVH分析中齿轮啮合特性研究［J］.振动工程学报，2010，23(6):681-686.Peng G M，Yu B，Ma X Y.Gear meshing characteristics of powertrain NVH analysis［J］.Journal of Vibration Engineering，2010，23(6):681-686(in Chinese).

［19］ Kahraman A，Singh R.Non-linear dynamics of a spur gear pair［J］.Journal of Sound and Vibration，1990，142(1):49-75.

［20］ Kahraman A.Effect of axial vibrations on the dynamics of a helical gear pair［J］.Journal of Vibration and Acoustics，1993，115(1):33-39.

［21］ Ognjanovic＇M，Kostic＇S C＇.Gear unit housing effect on the noise generation caused by gear teeth impacts［J］.Journal of Mechanical Engineering，2012，58(5):327-337.