近前视弹载SAR的改进后向投影成像算法

叶晓明，张国峰，胡晓光*，陈瑞国，孙艳鹤

(1.北京航空航天大学 虚拟现实技术与系统国家重点实验室，北京100191;2.国网辽宁省电力有限公司，沈阳110006;3.国网辽宁省电力有限公司检修分公司，沈阳110003)

弹载合成孔径雷达(SAR)导引头具有成像的功能，可以用来增加中远程攻击武器如巡航导弹的末制导精度［1-2］.在弹道的末制导阶段，采用弹载SAR可以得到攻击物体或者其周围标志性建筑外貌信息特征的实时图，通过与弹上计算机中的预存基准图进行匹配，得出导引头相对于目标物体或者预设弹道的横向和纵向数据偏差，从而修正导引头弹道并将导弹精确地导向打击目标.为了提高攻击的概率，在末制导阶段巡航导弹需要作高速机动的飞行.为了减小导弹攻击时的转弯曲率，弹载SAR需要尽早发现攻击目标，这样可以给导弹的高机动飞行留有充足的时间，从而避免导弹在高机动、大转弯时出现成像失效问题［3-4］.现有的弹载SAR侧视和普通斜视模式已经很难满足日益增长的末制导阶段成像需求，要求弹载SAR具有大斜视甚至近前视的成像能力［5-6］.

近年来，很多学者对大斜视弹载SAR从理论仿真和实际应用等方面都进行了深入的研究，相关研究主要从提高瞬时斜距模型近似处理的精度和距离走动校正(RCMC，Range Cell Migration Correction)的精度着手，对距离多普勒(RD，Range Doppler)、线调频变标(CS，Chirp Scaling)或者频谱分析(SPECAN，Spectral Analysis)类算法进行改进，取得了不少研究成果.2008年，李悦丽［7］针对弹载SAR大斜视角成像时距离走动的空变特性，提出了一种改进的方位向非线性CS大斜视角成像算法，可以处理50°的斜视角.2009年，易予生［8］针对 SAR斜视角较大时，分辨率要求较高和大测绘带成像的特点，结合了CS算法的优点，提出了一种改进的大斜视CS成像算法，可以处理70°的斜视角.2011年，彭岁阳［9］采用时域距离走动校正的改进RD算法，可以处理 50°的斜视角.2012 年，张刚等［10］针对大斜视状态下回波数据方位向和距离向严重耦合、弹载SAR平台实时性要求高的特点，提出了一种基于SPECAN算法的弹载SAR大斜视成像算法，可以处理60°的斜视角.现有的这些改进算法所处理的斜视角度有限，不能达到80°～86°的近前视成像，而且由于这些算法在成像处理中都存在各种近似，这些近似导致的误差会随着导弹运动状态的改变而改变，所以高机动的弹载SAR平台近前视成像的图像分辨率难以得到保证.

由此考虑到由 Mccorkle和 Rofheart［11］最早引入到SAR成像处理中的后向投影(BP)算法，它是一种精确的时域成像算法，没有直线运动的假设，不但适用于线性或者非线性弹道，而且得到的SAR图像没有波前弯曲和几何形变，因此非常适合高机动弹载SAR近前视成像.然而由于传统的BP算法在成像过程中需要进行大量的插值运算等操作，这会对实际中采用弹载SAR进行实时成像造成很大的影响.传统BP算法由于运算量巨大，影响实时成像，国内外学者对其进行了一系列的改进，Ulander等［12］提出了基于因式分解的后向投影成像算法，李杨寰等［13］提出了多级多分辨快速后向投影成像算法，李浩林等［14］提出了改进的快速分解后向投影SAR成像算法.这些算法在很大程度上解决了传统BP算法计算效率低的瓶颈问题.然而，在末制导阶段当要求弹载SAR的斜视角度达到近乎前视的80°～86°时，相同分辨率下成像积累的脉冲点数会多很多.由于现有的改进BP算法都是基于类似快速傅里叶变换蝶形分解模式，难以进行并行处理.

为了最大程度地提高BP算法的运算效率，使其能够满足高机动近前视弹载SAR成像的问题，本文引入文献［15］中的子孔径合并和图像分裂思想，提出一种改进的BP并行处理算法.该算法结合了已有的改进BP算法的快速性和精确聚焦性，并采用并行处理的方法，极大地降低了BP算法的运算量，提高了运算效率.最后的仿真实验证实了本文所提的算法不仅能满足高机动弹载SAR平台80°～86°近前视成像分辨率的要求，还能够实时地输出弹载SAR图像.

1 近前视弹载SAR回波信号模型

弹载SAR末制导阶段近前视成像场景如图1所示.导弹沿ABC弹道进行匀加速曲线运动，投影到地面上的xy平面，航向速度、侧向速度、天向速度分别为Vx，Vy和Vz，航向加速度、侧向加速度、天向加速度分别为ax，ay和az.方位向慢时间为ta，距离向快时间为tr，弹载SAR平台在ta=0时刻的位置是B点，此时距离地面的高度为H.设成像区域内任意一个目标为P点，其坐标为P(x0，y0，0)，导弹在 B 点时到 P 点的最小斜距，若弹载SAR近前视的斜视角为θ，那么

图1 弹载SAR末制导阶段近前视成像场景Fig.1 Imaging scene of approximate forward looking missile-borne SAR in terminal guidance stage

当导弹飞行到任意的ta时刻时，弹载SAR到攻击目标P之间的瞬时斜距可表示为R(ta)，根据图1中的几何关系可知:

从而可以推导出:

假设弹载SAR发射线性调频信号，则接收端经过相干检波处理后的基带信号可以表示为

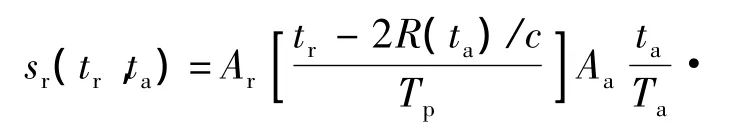
式中，Ar为矩形窗口，Aa为窗口波形，Ar与Aa共同组成回波的方位向和距离向的窗口函数;c为电磁波传播速度;Ta为弹载平台合成孔径时间;Tp为调频信号脉冲宽度;λ为载波波长;Kr为发射信号的距离向调频斜率;Rref为导弹与场景中心点的参考斜距;ΔR(ta)=R(ta)－Rref.距离压缩时会用到式(2)中的单频信号，方向位压缩时会用到方位向调频信号，那么在成像过程中需要消除剩余视频相位项

2 传统后向投影算法分析

后向投影算法最早用在计算机层析成像领域，Mccorkle 和 Rofheart［11］首先介绍了“时控阵”这个术语，详细地解释了BP算法，先求得回波的延迟时间，再相干累加回波，以此满足方位向的分辨率要求.

在BP算法之前要先对回波数据进行距离向的压缩，经过处理后的各个分割区域回波变成一个叠加曲线.当信号的时宽带宽积BrTp≫1时，式(2)变为

在距离频域对式(3)进行傅里叶变换，可得

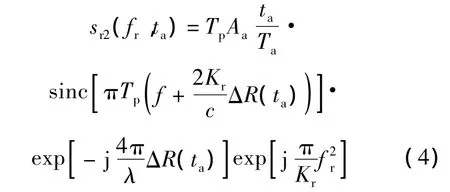
式中，fr为距离向频率;⊗tr代表卷积相乘.

根据式(4)，可以得到RVP校正因子表达式

将式(4)和式(5)相乘就可以消除RVP项，并且完成距离向压缩，这样式(4)变为

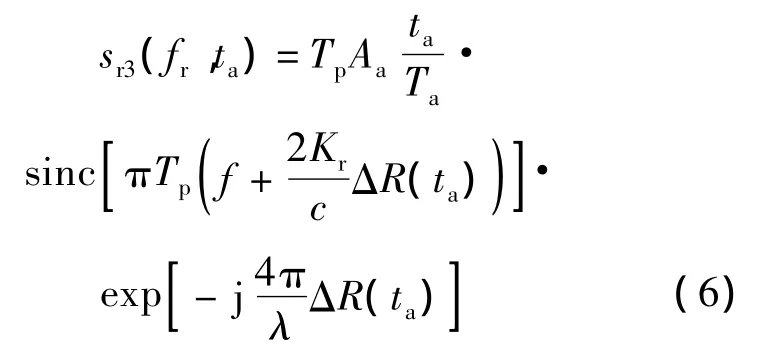
其次对方位向进行压缩，先将弹载SAR的扫描场景细化为一个点阵，找到点阵内每个点的累积回波曲线，然后对其上的值采取相干叠加，即可达到方位向压缩的目的，最终获得弹载SAR图像，可以表示为如下公式:

传统BP算法流程图如图2所示.

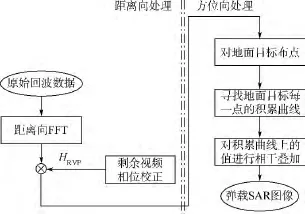
图2 传统BP算法流程图Fig.2 Flow chart of traditional BP algorithm

3 改进后向投影算法

本节提出的近前视弹载改进BP算法在距离向对回波数据的处理与传统BP算法是一样的，不同的是方位向的处理.首先在距离方向上对弹载SAR扫描场景进行等间隔分割，在合并子孔径的同时分裂图像，达到所需图像精度时停止合并和分裂，再相干叠加反向投影到扫描场景的分割小区域内的回波，这样就会得到扫描区域的弹载SAR图像.图3所示为弹载SAR扫描场景按条带划分示意图，正方形大区域的每一列表示弹载SAR扫描场景被分割后的一个小区域条.分割后的小区域条可以单独成像，因此比较适合并行处理.

图3 弹载SAR扫描场景按条带划分示意图Fig.3 Division schematic of missile-borne SAR scanning scene by stripe

在实际操作中，不用把所有天线扫描过的场景的回波数据都一一对应于弹载SAR图像，采用图3中任意一列区域条中的一个小正方形区域块来解释，将其放大，如图4中的正方形成像小块.图4所示为近前视模式后向投影误差分析图.导弹沿着图4中的弹道AB进行飞行，扫描过的场景发射的回波信号再反向投影到扫描场景CD区域，显然该区域不存在误差.导弹飞行到A点时，反映在扫面区域中的实际位置是P1点，经过反向投影到扫描区域的目标的位置近似为P2点.如果P1点和P2点都在相同的小正方形区域内，则认为这样的近似是合理的.

图4 近前视模式后向投影误差分析图Fig.4 Back-projection error analysis image of approximate forward looking model

后向投影产生误差的原因是，导弹在飞行过程中由于高机动而导致真实弹道与设定弹道不完全吻合.设弹道AB间距离为r，由图4中的几何关系，根据余弦定理可得

近似推导出距离向误差为

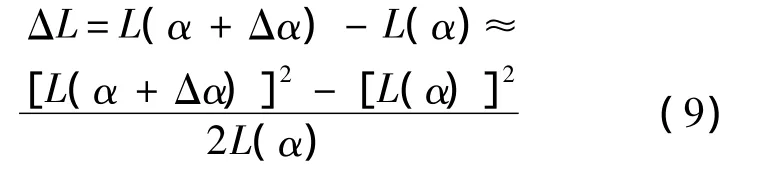
假定距离向误差比距离要小的多，即ΔL≪L(α)，则式(9)变为

当角度误差Δα≪1时，设DL为孔径的长度，可以得到

假定弹载SAR扫描场景大小为DL×Da，其中Da为方位向长度，DL为距离向合成孔径长度.α增大，距离向误差也会跟着变大.从式(11)很容易看出距离向的近似误差最大值为

式中Lmin为弹载SAR到扫描场景的最短距离.由式(12)可以看出，当DLDa的值恒定时，ΔL就会保持在合理的范围内.如果DL变大，那么Da相应地变小，ΔL即可维持不变.

为了使式(12)中的ΔL保持不变，采取对子孔径进行分级合并同时相应地对SAR图像进行分级分裂的方法，以此来分级叠加成像.图5所示为子孔径合并与条带图像分裂图.子孔径以2为幂级数按照16，8，4，2，1 进行分级合并，在这个过程中波束宽度缓慢变小，从而能够成像的场景也会变小，为了使距离向误差保持不变，同时会以2为幂级数按照1，2，4，8，16对区域条进行细等分成次级区域块，当方位向分辨率达到所需要求时，就不再继续合并子孔径和细分区域条.

图5 子孔径合并与条带图像分裂图Fig.5 Combine sub-aperture and divide stripe image

由于每个区域条内的成像算法一致，因此可以选取单个区域条为例进行算法描述.首先计算初始孔径到初始图像中心间的距离，其中为第1级的第i个子孔径为第1级的第k个子图像中心，并从距离向聚焦后的图像中寻找成像数据每一级的孔径到对应的图像的距离为通过上一级的成像数据得出当前级的成像数据，其中

继续进行下一级的子孔径合并和图像细分，当图像分辨率达到所需要求时，不再往下合并和细分.累加每一级的成像数据就可以得这个区域条的图像.最后把所有区域条的图像整合到一起就成为完整的SAR图像.

近前视弹载SAR改进BP算法流程图如图6所示.

图6 近前视弹载SAR改进BP算法流程图Fig.6 Flowchart of improved BP algorithm of approximate forward looking missile-borne SAR

4 运算量分析

在对改进BP算法进行性能分析时，考虑最简单的例子，即子孔径合并和图像细分都只需两级.孔径距离向长为L，首先将其划分成I个子孔径，长为LI，在这个过程中同时把M×N的扫描场景切割成K个区域条，大小为M×NK，其中M表示方位向长度，N表示距离向长度.其次将子孔径的回波数据投影到对应的区域条上，再将子孔径回波数据投影到区域条上的小区域块上.最后要对回波数据采取插值等操作，这样使得回波数据得以相干累加.令插值因子为η，则整个操作的运算量为ηLI(I×N+N×M).

再考虑通用的情况，可以将后向投影算法分成P步完成.若L＞N=M=Kn，n为运算的步骤数，随着分级数的增加，孔径长度会变大，同时图像分辨率也会提高，直到最后获取达到分辨率要求的弹载SAR图像.每一次分级的运算量为η×(K－1)×N×M，改进算法需要的总运算量为η×n×(K－1)×N×M.

对孔径和图像处理可以得到任意分解的算法，如L=L1L2…LI.当I=1和L=LI时，就是传统的BP算法，传统 BP算法所需的运算量为L×N×M.

对于高分辨SAR，8倍插值时能满足成像精度的要求，即取 η=8，这样加速比为当N＞64时,，即改进BP算法的运算量小于传统BP算法的运算量，N和加速比的变化方向一致.N取4 096的时候，改进BP算法的速度是传统BP算法速度的近43倍，改进BP算法与传统BP算法相比的加速比如图7所示.

图7 改进BP算法与传统BP算法相比的加速比Fig.7 Speed-up ratio of improved BP algorithm and traditional BP algorithm

此外，由于每个条带之间的成像是相互独立的，因此可以采用并行处理的方法，改进算法的运算速度可以得到进一步提高.

5 仿真实验

为了验证算法的有效性，从仿真回波数据和实测回波数据2个方面进行实验.所有实验在同一计算机上的MATLAB(R2014a版本)环境下运行，计算机处理器核为Intel Ivy Bridge Core(TM)i7-3770S CPU，内存为 16 GB，主频为3.10 GHz.

5.1 仿真数据实验

为了验证改进BP算法的有效性，对地面的一重型坦克目标进行86°近前视弹载SAR成像仿真，仿真参数如表1所示.本实验在采用Matlab进行仿真实验时，未采用处理器的并行处理功能，只做线性算法处理.

表1 近前视弹载SAR仿真参数Table1 Simulation parameters of approximate forward looking missile-borne SAR

在末制导阶段的初始时刻，设定导弹的位置坐标为(－400，－550，16 000).弹载 SAR 天线扫描区域内有一重型坦克目标，重型坦克目标强散射点分布示意图如图8所示，它有20个比较强的散射中心，标号1～20的散射中心点的位置坐标(单位为 m)分别为 1(－ 3，18，0)，2(3，18，0)，3(－6，12，0)，4(－ 3，12，0)，5(3，12，0)，6(6，12，0)，7(－6，6，0)，8(0，6，0)，9(6，6，0)，10(－6，0，0)，11(0，0，0)，12(6，0，0)，13(－6，－6，0)，14(0，－6，0)，15(6，－6，0)，16(0，－9，0)，17(－6，－12，0)，18(－3，－12，0)，19(3，12，0)，20(6，12，0).

分别利用传统BP算法和本文改进BP算法对该坦克目标进行成像，仿真坦克数据成像结果如图9所示，其中图9(a)为传统BP算法的成像结果，图9(b)为本文改进BP算法的成像结果.

由图9(a)和图9(b)可以看出，传统BP算法和本文改进BP算法都可以对仿真坦克数据精确成像，成像结果和坦克的20个强散射中心的坐标值基本一致.

下面对强散射中心点的脉冲响应进行成像质量评价.如图10与图11所示分别为传统BP算法和本文改进BP算法的强散射中心成像等高线图.

图8 重型坦克目标强散射点分布示意图Fig.8 Distribution schematic of strong scattering target points of male tank

图9 仿真坦克数据成像结果Fig.9 Imaging results of simulation tank data

对比图10和图11可以看出，强散射中心点1，3，9，11，13 和20 的成像效果差不多，都在可接受的范围内.这是因为BP算法不用进行距离徙动校正也可以获取高精度的SAR图像，不像现有的其他算法还需要解决深度聚焦问题.

为了同其他改进算法比较成像质量指标性能，将坦克强散射中心成像结果评价指标列于表2中.

图10 传统BP算法强散射中心成像等高线图Fig.10 Contour maps of strong scattering center imaging in traditional BP algorithm

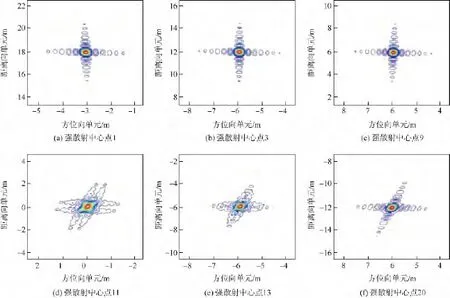
图11 本文改进BP算法强散射中心成像等高线图Fig.11 Contour maps of strong scattering center imaging in improved BP algorithm of this paper

由表2的结果可以分析出，本文改进BP算法的各性能指标数据与所列文献的改进算法的各性能指标数据差不多，峰值旁瓣比(PSLR)、积分旁瓣比(ISLR)及分辨率这3个指标都稍差于传统BP算法的，但这并不影响导弹获得正确的SAR图像信息.从运算时间上来看，仿真实验中传统BP算法需要26.4 s的时间，而本文改进的BP算法仅需要2.6s，与表2中其他的改进BP算法的速度相当.通过实验还得知，当不包括算法的预处理以及输出等处理时间时，核心算法的处理时间基本上能够达到理论加速比.

表2 坦克强散射中心成像结果评价指标Table2 Evaluating indicator of strong scattering center imaging results of tank

为了进一步体现本文算法在硬件实现上的运算时间优势，将文献［12-14］以及本文的算法移植到自主研发的以TMS320C6713为核心处理器的8片DSP并行高速信号处理板上，各算法在多DSP处理器上的运算时间如表3所示.

表3 各算法在多DSP处理器上的运算时间Table3 Run time of each algorithm on multi-DSP processor s

由于本文改进的BP算法是按条带进行独立成像的，可以对回波数据进行并行处理，配合目前多核并行处理的DSP芯片，成像时间可以得到进一步缩短，从而在运算时间上也会优于现有的其他改进BP算法.这样，本文改进的BP算法更加符合近前视弹载SAR成像的高实时性要求.

5.2 实测回波数据实验

采用传统BP算法和本文改进BP算法对实测的回波数据进行成像实验，以做更进一步的验证.弹载SAR相关参数如下:载频为16.5 GHz，信号带宽为200 MHz，脉冲重复频率为13.653 kHz，脉冲宽度为 26.67 μs，高度为 15 km，斜视角为86°，航向速度为 900 m/s，侧向速度为 100 m/s，天向速度为600 m/s，采样率为120 MHz，参考距离为3652 m.传统BP算法对实测回波数据的成像结果如图12(a)所示，成像耗时5786 s，本文改进BP算法对实测回波数据的成像结果如图12(b)所示，成像耗时613 s.

从图12中可以看出，本文改进BP算法获取的近前视弹载SAR图像基本上能达到传统BP算法的成像效果，但是传统BP算法的运算时间是本文改进算法的9.4倍，这与5.1节的仿真结果类似.在此基础上，若再对本文改进BP算法采用并行处理，那么成像速度亦会得到大幅度的提高.

图12 对实测回波数据的成像结果Fig.12 Imaging results of measured echo data

6 结论

本文在对近前视弹载SAR几何关系和传统BP算法详细分析的基础上，提出了一种适于并行处理的改进BP算法.得到的结论如下:

1)本文通过对斜视角为86°的扫描场景进行成像，通过与现有的各种典型的改进BP算法比较，结果验证了本文改进算法的有效性和可行性，SAR图像评价指标结果说明了本文算法的高精度性和快速性.

2)在运算时间和成像延迟方面，由于本文改进算法适于并行处理，若配合多核高性能DSP芯片，其成像速度也会高于现有其他算法的成像速度.

3)通过对86°斜视角实测回波数据进行成像，所得的SAR图像进一步证实了本文改进算法在精确制导领域的实用性.

References)

［1］ 保铮，邢孟道，王彤.雷达成像技术［M］.北京:电子工业出版社，2005:146-151.Bao Z，Xing M D，Wang T.Radar imaging technique［M］.Beijing:Publishing House of Electronics Industry，2005:146-151(in Chinese).

［2］ 彭岁阳，胡卫东，杜小勇.一种基于合成带宽技术提高SAR分辨率的新方法［J］.信号处理，2010，26(1):12-16.Peng S Y，Hu W D，Du X Y.A new method for improving SAR resolution based on synthesized bandwith technique［J］.Signal Processing，2010，26(1):12-16(in Chinese).

［3］ 吴勇，宋红军，彭靳.基于时域去走动的SAR大斜视CS成像算法［J］.电子与信息学报，2010，32(3):593-598.Wu Y，Song H J，Peng J.Chirp scaling imaging algorithm of SAR in high squint mode based on range walk removal［J］.Journal of Electronics ＆ Information Technology，2010，32(3):593-598(in Chinese).

［4］ Sun X，Yeo T S，Zhang C，et al.Time-varying step-transform algorithm for high squint SAR imaging［J］.IEEE Transactions on Aerospace and Electronic Systems，1999，37(6):2668-2677.

［5］ 俞根苗，邓海涛，张长耀，等.弹载侧视SAR成像及几何校正研究［J］.系统工程与电子技术，2006，28(7):997-1001.Yu G M，Deng H T，Zhang C Y，et al.Study of imaging processing and geometric correction of missile-borne side-looking SAR［J］.Systems Engineering and Electronics，2006，28(7):997-1001(in Chinese).

［6］ 张泽云，赵宏生，徐朝阳.基于 ADSP-TS201S的雷达信号处理研究［J］.舰船电子对抗，2011，34(3):46-48.Zhang Z Y，Zhao H S，Xu C Y.Research into radar signal processing based on ADSP-TS201S［J］.Shipboard Electronic Countermeasure，2011，34(3):46-48(in Chinese).

［7］ 李悦丽.弹载合成孔径雷达成像技术研究［D］.湖南:国防科学技术大学，2008.Li Y L.The imaging techniques of missile-borne synthetic aperture radar［D］.Hunan:National University of Defense Technology，2008(in Chinese).

［8］ 易予生.弹载合成孔径雷达成像算法研究［D］.西安:西安电子科技大学，2009.Yi Y S.Research on imaging algorithm for the missile-borne synthetic aperture radar［D］.Xi’an:Xidian University，2009(in Chinese).

［9］ 彭岁阳.弹载合成孔径雷达成像关键技术研究［D］.长沙:国防科学技术大学，2011.Peng S Y.Research on key technologies of missile-borne synthetic aperture radar imaging［D］.Changsha:National University of Defense Technology，2011(in Chinese).

［10］ 张刚，杨立波，祝明波，等.弹载SAR大斜视SPECAN成像算法［J］.无线电工程，2012，42(11):10-13.Zhang G，Yang L B，Zhu M B，et al.SPECAN imaging algorithm for missile-borne SAR with high squint angle［J］.Radio Engineering，2012，42(11):10-13(in Chinese).

［11］ Mccorkle J W，Rofheart M.An order N2log2(N)back projector algorithm for focusing wide-angle wide-bandwidth arbitrarymotion synthetic aperture radar［J］.Proceedings of SPIE on Radar Sensor Technology，1996(2747):25-36.

［12］ Ulander L M H，Hellsten H，Stenström G.Syntheticaperture radar processing using fast factorized back-projection［J］.IEEE Transactions on Aerospace and Electronic Systems，2003，39(3):760-776.

［13］ 李杨寰，宋千，王鹏宇，等.多级多分辨快速后向投影成像算法［J］.电子学报，2011，39(3):518-524.Li Y H，Song Q，Wang P Y，et al.Multi-stage multi-resolution fast back-projection imaging algorithm［J］.Acta Electronica Sinica，2011，39(3):518-524(in Chinese).

［14］ 李浩林，张磊，杨磊，等.一种改进的快速分解后向投影SAR成像算法［J］.电子与信息学报，2013，35(6):1435-1441.Li H L，Zhang L，Yang L，et al.A novel fast factorized backprojection algorithm for synthetic aperture radar imaging［J］.Journal of Electronics ＆ Information Technology，2013，35(6):1435-1441(in Chinese).

［15］ Kaplan L M，McClellan J H，Seung M O.Prescreening during image formation for ultrawideband radar［J］.IEEE Transactions on Aerospace and Electronic Systems，2002，38(1):74-88.