轮盘概念设计中拓扑和形状同时优化方法

范俊，尹泽勇，王建军，米栋，3，闫成

(1.北京航空航天大学 能源与动力工程学院，北京100191;2.陆航研究所，北京101121;3.中航工业 航空动力机械研究所，株洲412002)

结构优化包括拓扑、形状和尺寸优化3个阶段，对于前2个优化阶段，通常的优化顺序是，先进行拓扑优化，在拓扑优化结果的基础上，再进行形状优化.在这种分步进行的优化过程中，需要人为设定一个大小一定的不可调的初始设计区域用于拓扑优化;并且在基于变密度法(即SIMP法)的拓扑优化过程结束后，还需要人为设定一个用于删除中间密度单元的相对密度门槛值.然而，假如这两种人为设定参数选择不恰当，就有可能使得优化结果并不是最优解.

为了减小上述两类人为选择参数对优化结果的影响，本文提出了一种拓扑和形状同时优化(STSO)的方法.国外学者 Deaton等［1］认为从拓扑优化结果到形状优化初始设计模型的转化，是未来连续体多学科拓扑优化研究重点之一.Ansola等［2］论述了一个形状和拓扑组合优化的方法，在该方法中，交替进行形状和拓扑优化步骤，而在每一个步骤中，先进行形状优化再进行拓扑优化;这些步骤不断重复，直到得到一个收敛的全局解.Hassani等［3］论述了一个板壳结构形状和拓扑同时优化的方法，在该方法中，形状和拓扑优化不是分开进行的，而是并行的.上述两篇文献除了优化流程不一致之外，在优化算法上也是不一样的，Ansola采取的是单纯形法，Hassani采取的是移动渐进线法.国内学者张卫红等［4］为了解决压力载荷作用下的结构轻量化设计问题，直接采用B样条曲线描述压力加载面，通过拓扑和形状变量的联合优化满足了工程实际对结构轻量化与边界的功能性与光滑性设计要求.虽然本文中的拓扑和形状优化也是并行的，但与上述文献只考虑应变能和应力优化响应不同，本文的优化模型中还考虑了以频率为约束的三维实体结构(轮盘)动力学优化，采用的优化算法是序列二次规划优化算法(SQP法).

轮盘是航空发动机中关键部件，已有文献对轮盘进行了拓扑优化设计研究.文献［5］以体积刚度比为目标，应力、破裂转速、低循环疲劳寿命为约束建立拓扑优化数学模型，采用基于随机抽样敏度分析的双向渐进结构拓扑优化方法，得到了航空发动机双辐板形式的涡轮盘结构.文献［6］以体积刚度比为目标、应力为约束建立了拓扑优化数学模型，采用基于自适应随机抽样策略的周期结构拓扑优化方法得到了多辐板风扇盘.文献［7］以最小体积为目标、应力为约束建立了典型风扇盘子午面结构优化设计模型，得到了一个多辐板盘结构.从国外先进的发动机来看，许多高性能发动机宽弦风扇盘经过拓扑优化设计，选用了多辐板的盘毂混合式轮盘结构［6］，如CFM56-7，RB211-535E4等采用了双辐板轮盘结构.但是，上述文献一般只考虑了静力学目标和约束，且拓扑和形状优化都是分步进行的.为了设计出既轻且刚性适当又安全可靠的轮盘，有必要研究轮盘的模态特性，进行与实体轮盘频率等有关的动力学优化设计.

本文首先建立了基于SIMP法的拓扑和形状同时优化(STSO)数学模型，分析了相应的灵敏度，使用SQP法进行求解.然后，以板壳结构为例，进行了拓扑和形状同时优化，将其结果与分步优化进行比对，探讨了相对密度门槛值的选取和两种优化变量之间的相互作用对最终优化结果的影响，说明拓扑和形状同时优化的优点.最后，本文将同时优化的方法应用于轮盘概念设计中，对比分析了不同振型所对应的频率约束时实体轮盘拓扑和形状同时优化方法与单独拓扑优化方法的不同结果.

1 STSO方法数学模型

SIMP法是拓扑优化方法的一种，由于其数学论证严密、便于实施等优点而得到广泛应用［8-9］.本文的STSO方法将基于SIMP法来展开研究.

SIMP法建立在结构有限元模型的基础上，设计变量是各单元的相对密度，是在［0，1］区间的连续变量，第 i个单元的相对密度用 ρi来表示(i=1，2，…，N)，N指单元总数.设单元的原始密度是 ρ，优化后密度是 ρe，则存在关系式 ρi= ρe/ρ;SIMP法中，单元材料属性是单元相对密度的指数函数，设第i个单元初始和优化后的弹性模量分别是E0，Ei(ρi)，第i个单元初始和优化后的刚度矩阵分别是K0i，Ki(ρi)，则存在关系式:

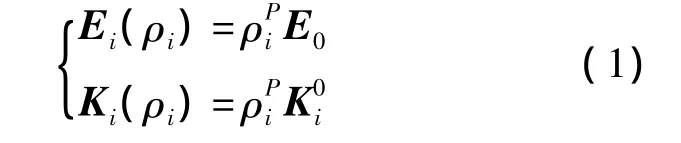
式中P为惩罚因子，其作用是对中间相对密度进行惩罚，使结构单元相对密度尽可能趋于0或者1.用于航空发动机轮盘拓扑和形状优化的数学模型是以体积、应力和频率为约束，以最小化结构应变能为目标.

式中，C为应变能;F为载荷;U为位移;σeq为当量应力;σ0.1为 0.1% 屈服强度;V0i为第i个单元的初始体积;V为优化之后结构体积;V0为结构原始体积;V0iρi为优化后单元的等效体积;g(f)为频率f的函数;K为全局刚度阵;M为全局质量阵;λ为特征值;φ为对应的特征向量;Di为第i个节点的位移矢量;D为一个位移常量;j和为形状优化变量yj的上下限.

2 灵敏度分析

灵敏度分析包括拓扑优化变量和形状优化变量灵敏度分析两个部分，本文着重分析目标和约束对拓扑优化变量的灵敏度.

2.1 频率灵敏度

频率约束的灵敏度，是通过多自由度无阻尼系统自由振动的运动方程，利用特征值法求得.对式(2)中的运动方程，通过对特征向量用质量矩阵进行规格化［10-11］，则特征值对设计变量的导数可表示为

式中，λj为第j阶特征值;φj为第j阶特征值对应的特征向量.由于

式中，M0i为第i个单元的初始质量矩阵;Mi为第i个单元优化后的质量矩阵，所以

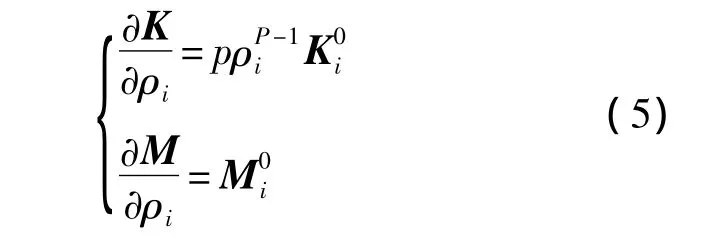
将式(5)代入式(3)，可得

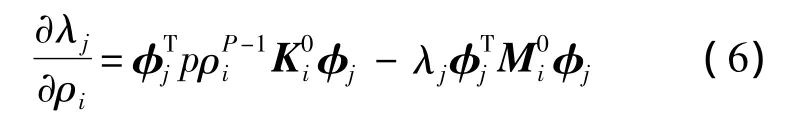
由 λj=f2j，可得

2.2 应变能、体积和位移灵敏度

由于式(2)中外力F是一个常量，则有

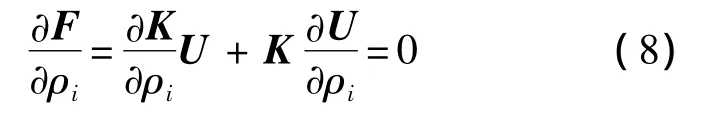
由于结构刚度矩阵的对称性，并将式(8)代入可得应变能的灵敏度为

容易得到，体积约束的灵敏度为

由式(8)可得位移灵敏度为

2.3 应力灵敏度

现阶段应力相关的优化问题面临着诸多的难题［12］，如优化过程中由于应力约束不连续导致的应力奇异现象、局部应力约束过多导致的超大计算规模等计算难题.隋允康等［13］等利用Mises强度理论，提出了应力约束全局化策略，将局部的应力约束问题转化为结构整体的应变能约束问题.荣见华等［14］在优化迭代循环的每一轮子循环迭代求解开始时，通过形成和引进新的位移和应力约束限，自动构建设计变量移动限，将结构应力约束归并为几个最可能的有效应力约束，从而减少应力灵敏度的分析量.París等［15］总结了连续体拓扑优化中应力约束灵敏度分析的一般方法.

式(2)中第i号单元的VonMises应力近似地可以表示为

式中，Bhi为第i号单元的第h个高斯积分点的几何矩阵;ni为第i号单元的高斯积分点数;Ui为仅与第i号单元所有自由度相应的U中元素构成的单元位移矢量.则应力灵敏度为

由式(11)可以求得∂Ui/∂ρi为∂U/∂ρi中与第i号单元所有自由度相应元素构成的矢量，将其代入式(13)，则可以求得应力灵敏度.

对于形状优化变量的灵敏度，并不能十分明确地列出［3］.在本文中，采用一种半解析的办法，这样，形状优化变量的灵敏度一部分由解析解推出来，一部分由有限差分近似推出来，具体的推导见文献［16-18］.

在求得目标和约束函数的灵敏度基础上，运用SQP法进行求解，SQP算法具体原理可参考文献［19-20］.

3 分步优化和同时优化对比分析

以图1中的板壳结构为例来进行对比分析，待优化的板长度为100mm，宽度为10mm，厚度为1 mm，划分成1000个1×1的单元.

板的左端受全约束，板的右端上顶点处施加100 N的集中力.材料的弹性模量是 2.1×105MPa，泊松比是0.3.优化的设计区域是整个黄色区域.为了对比分步优化和同时优化结果，相比于式(2)，减少了频率和应力约束，将优化目标改为体积最小，约束是板的右端下顶点的位移小于3 mm，建立数学模型见式(14).

式中d101为第101个节点的垂直位移，该节点位于板的右端下顶点.

图1 结构优化的初始有限元模型Fig.1 Original finite element model for structural optimization

3.1 先拓扑后形状分步优化

图2(a)描述了通常一般优化顺序:先进行拓扑优化，在拓扑优化结果的基础上，再进行形状优化.其中，在基于SIMP法的拓扑优化过程中，并不删除单元，而是通过改变单元的相对密度值来满足约束条件.在拓扑优化过程结束后，需要人为设定相对密度门槛值，删除低于该值的单元后，得到最终拓扑优化结果，用于形状优化.

图2 结构优化流程Fig.2 Flow of structure optimization

按照这个优化顺序，先对图1中的板壳结构进行拓扑优化，迭代25步收敛，取相对密度门槛值为0.16，删除相对密度小于该值的单元，得到的拓扑优化结果如图3(a)所示.然后，定义该结果中的形状优化变量.本文出于演示论证的目的，只定义了一个形状优化变量.设形状变量为图形上边界中点处节点的位置，该节点可上下移动.同样采用SQP算法，迭代3步后收敛，得到的结果如图3(b)所示.从结果看出，在拓扑结构一定的情况下，进行形状优化，其拓扑构型并没有改变，只是形状的边界尺寸发生了变化，优化的效果不明显.

图3 拓扑优化结果及基于拓扑优化的形状优化结果Fig.3 Topology optimization result and shape optimization result based on topology optimization

因此，拓扑优化结果对于后续的优化有着重要的作用，而人为选定的相对密度门槛值对拓扑优化结果有着重要的影响.为了减小这种主观选择参数对结果的影响，有必要拓扑和形状同时优化.

3.2 先形状后拓扑分步优化

不同的初始设计模型会产生不同的拓扑优化结果，为了得到较好的拓扑优化结果，文献［2］认为，应该先通过形状优化来确定初始设计模型，再进行拓扑优化.本文将以算例表明，先形状后拓扑的优化流程也并不一定能得到最优解.

对于图1所示模型，先进行形状优化，以确定用于拓扑优化的初始设计模型.定义两个形状优化变量:一是模型上边界右端顶点处节点的位置，该节点可以上下移动;二是模型上边界中间点处节点的位置，该节点可以上下移动.优化在迭代5步后收敛，得到的形状优化结果如图4(a)所示.将该形状优化结果作为初始设计模型，再进行拓扑优化，迭代5步后收敛，得到的拓扑优化结果如图4(b)所示.从图中可以看出，在形状优化结果基础上再拓扑优化，发生的改变并不多.这也表明，经过形状优化确定的初始设计模型，不一定是最合适的用于拓扑优化的初始设计模型;同时从图3(a)和图4(b)的比对看出，不同的初始设计模型进行拓扑优化会产生不同的优化解.

图4 形状优化结果及基于形状优化的拓扑优化结果Fig.4 Shape optimization result and topology optimization result based on shape optimization

3.3 拓扑和形状同时优化

在分步优化过程中，人为设定的初始设计区域和相对密度门槛值，对最终优化结果有着重要的影响，为了减小这种人为设定参数的影响，本节使用拓扑和形状同时优化的方法对该板壳结构进行优化.

对图1中的初始设计模型，进行拓扑和形状同时优化，其中，形状优化变量与3.2节保持一致.优化的流程如图2(b)所示，迭代59步后得到STSO优化结果如图5(a)所示，优化结果类似于桁架结构.该结果的重量已经较小，可直接进入详细设计阶段对应的尺寸优化.

图5 形状和拓扑同时优化结果Fig.5 Simultaneous shape and topology optimization result

因为3.1节和3.2节所述分步优化过程中，第2步优化的效果相比于第1步要小得多，图5(b)中描述了两种分步优化方法的第1步优化结果(体积)和同时优化结果随优化步数变化趋势.从图中可以看出，相比于分步优化，同时优化后的结构体积要小得多，这说明同时优化方法的效果是最好的.

此外，从上述的优化结果对比分析看，形状和拓扑优化是一个整体，是相互作用的两个过程，割裂地进行优化有可能得不到全局最优解.

4 STSO方法在轮盘概念设计阶段的应用

4.1 初始设计模型

使用STSO方法优化的轮盘是一个全三维模型，该模型所参考的航空发动机涡轮盘子午面如图6(a)所示［4］.其中，中心孔半径 Rb=65 mm，轮缘半径Rr=278.6 mm，轮缘宽度Wr=44 mm，轮缘高度Hr=11.4mm，轮毂宽度Wb=91mm;轮缘均布载荷Pr=169.39 MPa，工作转速 N=13333 r/min;轮盘所用的材料为 GH4169，文中计算采用了600°C时该材料的性能参数.

图6(b)是用于结构优化的初始设计模型，其中蓝色非设计区域与参考盘的轮缘部分是一致的;绿色设计区域宽度参考轮毂宽度，将其暂定为Wb=160 mm，绿色设计区域高度为Rr－Rb－Hr=202.2 mm.

STSO方法在轮盘应用中的优化数学模型除了不考虑位移约束外，与式(2)所示相同.需要说明的是，本文目的主要是阐述STSO方法和概念，如图2(c)所示，该方法是应用于轮盘概念设计阶段，其优化结果距实际应用还有较长距离.因此，虽然轮盘不同的地方应有不同的应力约束条件，但是为了突出动力学优化以及对比STSO方法和单独拓扑优化方法的优劣，本文将各个地方的静力学要求简化为0.1%屈服极限的6/10.

另外，在STSO方法中，形状优化设计变量为图6(b)中4个角点(1，2，3，4 点)水平方向的位置，为了获取最佳的初始设计区域，将其变化范围设为［－80，80］;拓扑优化设计变量为绿色区域单元的相对密度值.

4.2 STSO方法在轮盘概念设计阶段的应用

图6中初始设计模型的第4阶和第5阶频率是679 Hz和1060 Hz，其振型如图7所示，分别是节圆和节径振动.从第3节可知，分步优化中第2步优化的效果相比于第1步要小得多，并且同时优化方法所得的优化结果如有必要也可以用形状和尺寸优化方法进行进一步的细节设计，因此，本节将运用STSO方法和单独拓扑优化方法对该轮盘进行结构优化，对比分析两种不同方法下不同振型对应的频率约束对轮盘优化结果结构形式的影响.

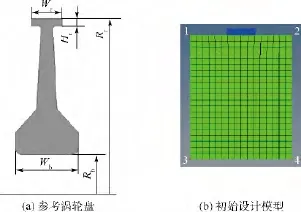
图6 初始设计模型Fig.6 Initial design model

图7 初始设计模型的第4和第5阶振型Fig.7 Fourth and fifth mode of vibration of initial design model

4.2.1 降低节径振动频率

将式(2)中的频率约束g(f)≤0确定为降低节径振动频率约束为f5≤900.单独进行拓扑优化，得到的优化结果见图8(a)所示;拓扑和形状同时优化的结果如图8(b)所示.

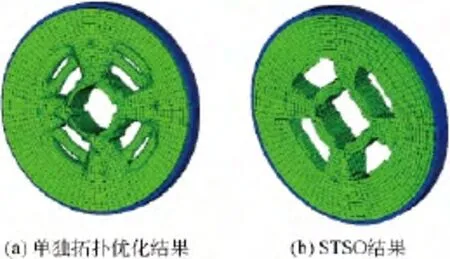
图8 降低节径振动频率的优化结果对比Fig.8 Comparison of optimization results with lower frequency of nodal diameter vibration

从结果看，两种方法得到优化结果拓扑形式是不一样的，同时优化结果拓扑形式较单独拓扑优化结果更为简洁.

图9分别列出了拓扑和形状同时优化，以及单独拓扑优化的应变能、频率、体积分数(优化后的体积与初始体积的比值)随迭代步数变化情况.从图中可以看出，两种优化的频率和体积约束在最后迭代步均分别达到相应上限值，而优化的目标——应变能则不同，拓扑和形状同时优化结果的应变能较单独拓扑优化的应变能更小，减小了约2.4%，并且其收敛速度较快.

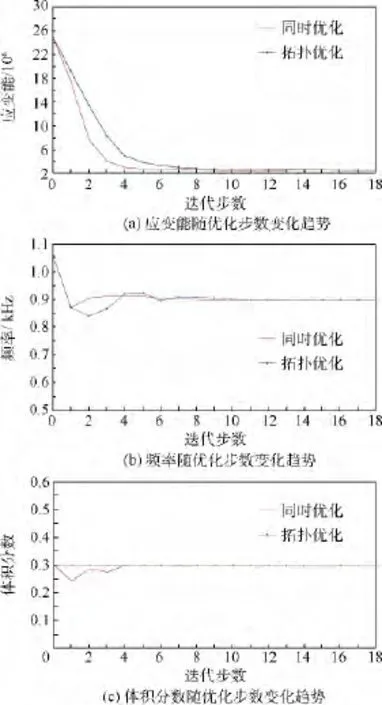
图9 降低节径振动频率的优化结果随迭代步数变化趋势对比Fig.9 Variation tendency comparison of optimization results with lower frequency of nodal diameter vibration in different iteration steps

4.2.2 提高节径振动频率

明确式(2)中的频率约束，提高节径振动频率约束为f5≥1100，优化结果如图10所示.图中给出的是优化后相对密度的分布情况(删除了较小相对密度单元的优化结果)，红色表示优化后相对密度较高的单元颜色，蓝色表示优化后相对密度较低的单元颜色.

在图10(a)和图10(b)中，当使用单独拓扑优化方法时，优化结果出现了开孔现象.而在图10(c)和图10(d)中，当使用STSO方法时，优化结果与参考盘类似，是一个单幅板的轮盘，并未出现开孔现象.

相较于单独拓扑优化方法的结果，使用STSO方法得到的结果，更符合现役发动机少有开孔轮盘的现状.

图11也分别列出了拓扑和形状同时优化，以及单独拓扑优化的应变能、频率、体积随迭代步数变化情况.从图中可以看出，两种优化的体积约束在最后迭代步均达到相应上限值，而优化的目标——应变能则不同，拓扑和形状同时优化结果的应变能较单独拓扑优化的应变能更小，减小了约8.5%，并且其收敛速度较快.

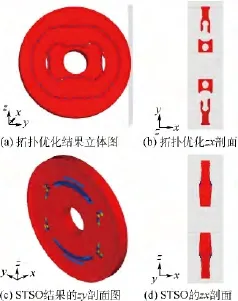
图10 提高节径振动频率的优化结果对比Fig.10 Comparison of optimization results with higher frequency of nodal diameter vibration

图11 提高节径振动频率的优化结果随迭代步数变化趋势对比Fig.11 Variation tendency comparison of optimization results with higher frequency of nodal diameter vibration in different iteration steps

4.2.3 提高节圆振动频率

明确式(2)中的频率约束，提高节圆振动频率约束为f4≥700，优化结果如图12所示.从图中可以看出，与单独拓扑优化结果类似，拓扑和形状同时优化得到了类似于双幅板形式的结构.二者不同的是，同时优化结果的幅板之间的间隔更小.

图12 提高节圆振动频率的优化结果对比Fig.12 Comparison of optimization results with higher frequency of umbrella vibration

图12(d)所示的双幅板涡轮盘拓扑形式，经过完善约束条件，以及在该优化结果基础上进一步的形状和尺寸优化，是能够应用于工程实践的.美国空军 CRRT计划［5］中采用了类似于图12(d)(如图12)的双幅板涡轮盘而取得了明显效果.

图13分别列出了拓扑和形状同时拓扑优化，以及单独拓扑优化的应变能、频率、体积随迭代步数变化情况.从图中可以看出，两种优化的体积约束在最后迭代步均达到相应上限值，而优化的目标——应变能则不同，拓扑和形状同时优化结果的应变能较单独拓扑优化的应变能更小，减小了约28.3%，并且其收敛速度较快.

4.2.4 降低节圆振动频率

明确式(2)中的频率约束，降低节圆振动频率约束为f4≤500，优化结果如图14所示.

图13 提高节圆振动频率的优化结果随迭代步数变化趋势对比Fig.13 Variation tendency comparison of optimization results with higher frequency of umbrella vibration in different iteration steps

图14 降低节圆振动频率的拓扑和形状同时拓扑优化结果Fig.14 Results of simultaneous topology and shape optimization with lower frequency of umbrella vibration

形状优化变量使得初始设计模型中轮盘中心孔处的厚度不断变化，但是如果厚度过小，如图14(b)所示，会使该处单元的边长比过大，而导致在优化过程中由于网格畸变过大，使得优化过程提前终止，这样的优化结果是无效的.图15描述了此时中心孔处单元边长比达到117，超过了上限值(该值等于100).

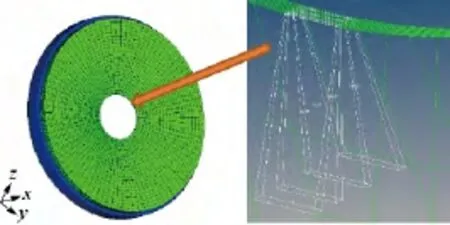
图15 边长比过大的单元Fig.15 Elements with overlarge aspect ratio

为了得到合适的优化结果，需修改形状优化设计变量的取值范围，由前述的［－80，80］改为［－25，25］，使用同时优化方法得到的结果如图16(c)、图16(d)所示.与单独拓扑优化方法所得结果类似，均为单幅板形式的拓扑.

图16 降低节圆振动频率的优化结果对比Fig.16 Comparison of optimization results with lower frequency of umbrella vibration

使用同时优化方法所得结构的应变能较单独拓扑优化方法所得结构，减小3.25%，如图17所示.

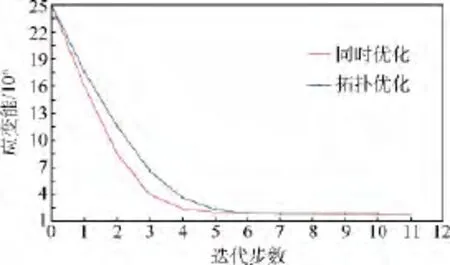
图17 降低节圆振动频率优化结果的应变能随迭代步数变化趋势对比Fig.17 Variation tendency comparison of strain energy of optimization results with lower frequency of umbrella vibration in different iteration steps

总的来看，STSO方法的优点是系统、准确、收敛快.它的局限性除了易引起网格畸变过大外，还在于将STSO方法应用于轮盘优化中时，并不能直接将优化结果应用于工程实践中.这是由于STSO方法只能包含初始设计模型中的形状优化变量，对于STSO方法的优化结果中新出现的拓扑构型，依然需要设置相应的形状优化变量，进行进一步的形状和尺寸优化等细化设计.因此，从这个方面看，STSO方法只是对应于结构的概念设计阶段，如图2(c)所示.

从概念设计阶段的结果到工程实际应用的轮盘，需要再考虑的因素较多，比如满足其他静力学约束，降低某阶次频率同时、提高另外阶次频率，热应力约束等.本文仅仅是运用STSO方法考虑了振型对应的频率约束对同时优化方法所得结果的影响，得到了几种概念设计方案，在本文所用STSO方法得到的优化结果的基础上，还需要进一步的形状和尺寸优化.

5 结论

本文首先建立了STSO方法的数学模型，并推导了目标和约束函数的灵敏度，运用SQP算法进行求解.用板壳结构优化的例子对比分析了同时优化和分步优化结果.将同时优化的方法用于轮盘动力学优化，分析了不同振型时频率约束对同时优化方法所得结果的影响，并将之与单独拓扑优化结果进行比较，结果表明:

1)拓扑和形状同时优化方法较分步优化减少了人为参与的环节，从优化过程看，更为客观科学.

2)拓扑和形状同时优化考虑了形状优化变量和拓扑优化变量之间的相互作用，回避了文献中所提出的拓扑和形状优化先后顺序问题，从整体看，更为系统化.

3)将拓扑和形状同时优化的方法应用于板壳结构优化和实体轮盘结构动力学优化时，结果表明，相较于分步拓扑优化和单独拓扑优化，同时优化方法的结果较分步优化效果更好，且收敛更快.

4)相较于轮盘单独拓扑优化方法结果，使用STSO方法得到的结果开孔较少甚至不开孔，更加符合现役发动机少有开孔轮盘的现状.

5)不同振型对应的频率约束不同时，得到了不同的优化结果.降低节径振动频率，均得到了辐条式拓扑;提高节圆振动频率，均得到了双幅板式拓扑;降低节圆振动频率，均得到了单幅板式拓扑.

6)由于形状优化变量取值范围选取不当，可能导致网格畸变过大而得到无效优化解，此时需要重新选择形状优化变量的取值范围.

References)

［1］ Deaton J D，Grandhi R V.A survey of structural and multidisciplinary continuum topology optimization:post 2000［J］.Struct Multidisc Optim，2014，49(1):1-38.

［2］ Ansola R，Canales J，Tarrago J A，et al.An integrated approach for shape and topology optimization of shell structures［J］.Computer ＆ Structures.2002，80(5):449-458.

［3］ Hassani B，Tavakkoli S M，Ghasemnejad H.Simultaneous shape and topology optimizationof shell structures［J］.Struct Multidisc Optim.2013，48(1):221-233.

［4］ 张卫红，杨军刚，朱继宏.压力载荷下的结构拓扑-形状协同优化［J］.航空学报，2009，30(12):2335-2341.Zhang W H，Yang J G，Zhu J H.Simultaneous topology and shape optimization of pressure loaded structures［J］.Acta Aeronautica et Astronautica Sinica，2009，30(12):2335-2341(in Chinese).

［5］ 刘超.涡轮盘结构拓扑与形状优化方法研究［D］.南京:南京航空航天大学，2010.Liu C.Topology and shape optimization method for turbine disk［D］.Nanjing:Nanjing University of Aeronautics and Astronautics，2010(in Chinese).

［6］ 宋健，温卫东，崔海涛，等.航空发动机多辐板风扇盘拓扑优化与形状优化设计技术［J］.推进技术，2013，34(9):1188-1196.Song J，Wen W D，Cui H T，et al.Topology and shape optimization method for multi-web fan disk in aero-engine［J］.Journal of Propulsion Technology，2013，34(9):1188-1196(in Chinese).

［7］ 李伦未，陆山.基于ANSYS的多辐板风扇盘结构优化设计技术［J］.航空动力学报，2011，26(10):2245-2250.Li L W，Lu S.Structure optimum design techniques for multi-web fan disk based on ANSYS［J］.Journal of Aerospace Power，2011，26(10):2245-2250(in Chinese).

［8］ 荣见华，唐国军，罗银燕，等.考虑位移要求的大型三维连续体结构拓扑优化数值技术研究［J］.工程力学，2007，24(3):20-27.Rong J H，Tang G J，Luo Y Y，et al.A research on the numerical topology optimization technology of large three-dimensional continuum structures considering displacement requirements［J］.Engineering Mechanics，2007，24(3):20-27(in Chinese).

［9］ 左孔天，陈立平，钟毅芳，等.基于人工材料密度的新型拓扑优化理论和算法研究［J］.机械工程学报，2004，40(12):31-37.Zuo K T，Chen L P，Zhong Y F，et al.New theory and algorithm research about topology optimization based on artificial material density［J］.Chinese Journal of Mechanical Engineering，2004，40(12):31-37(in Chinese).

［10］ 邹春江，左孔天，向宇，等.基于SIMP方法微电容加速度计结构固有频率拓扑优化［J］.科学技术与工程，2011，11(29):7086-7091.Zhou C J，Zuo K T，Xiang Y，et al.Natural frequency topology optimization for structure of micro-capacitive accelerometer based on SIMP method［J］.Science Technology and Engineering，2011，11(29):7086-7091(in Chinese).

［11］ 叶红玲，沈静娴，隋允康.频率约束的三维连续体结构动力拓扑优化设计［J］.力学学报，2012，44(6):1037-1045.Ye H L，Shen J X，Sui Y K.Dynamic topological optimal design of three-dimensional continuum structures with frequencies constraints［J］.Chinese Journal of Theoretical and Applied Mechanics，2012，44(6):1037-1045(in Chinese).

［12］ 张维声.基于水平集方法的应力相关拓扑优化问题研究［D］.大连:大连理工大学，2013.Zhang W S.Studies on stress-related topology optimization problem via level set approach［D］.Dalian:Dalian University of Technology，2013(in Chinese).

［13］ 隋允康，叶红玲，彭细荣.应力约束全局化策略下的连续体结构拓扑优化［J］.力学学报，2006，38(3):364-370.Sui Y K，Ye H L，Peng X R.Topological optimization of continuum structure under the strategy of globalization of stress constraints［J］.Chinese Journal of Theoretical and Applied Mechanics，2006，38(3):364-370(in Chinese).

［14］ 荣见华，葛森，邓果，等.基于位移和应力灵敏度的结构拓扑优化设计［J］.力学学报，2009，41(4):518-529.Rong J H，Ge S，Deng G，et al.Structure topological optimization based on displacement and stress sensitivity analysis［J］.Chinese Journal of Theoretical and Applied Mechanics，2009，41(4):518-529(in Chinese).

［15］ Paris J，Navarria F，Colominas I，et al.Stress constraints sensitivity analysis in structural topology optimization［J］.Computer Methodsin Applied Mechanicsand Engineering，2010，199(133):2110-2122.

［16］ Kai-Uwe B，Matthias F，Fernass D.Approximation of derivatives in semi-analytical structural optimization［J］.Computers ＆Structures，2008，86(13):1404-1416.

［17］ De Boer H，Van Keulen F.Refined semi-analytical design sensitivities［J］.International Journal of Solids and Structures，2000，37(46):6961-6980.

［18］ Van Keulen F，Haftka R T，Kim N H.Review of options for structural design sensitivity analysis.Part 1 linear systems［J］.Computer Methods in Applied Mechanics and Engineering，2005，194(30):3213-3243.

［19］ Fletche R.Practical methods of optimization［M］.New York:John Wiley and Sons，1987:304-319.

［20］ Nocedal J，Wright.S J.Numerical optimization［M］.New York:Springer Series in Operations Research，1999:529-561.