高精度多维限制器的性能分析
2015-12-20孙迪阎超于剑屈峰华俊
孙迪,阎超,于剑,屈峰,华俊
(北京航空航天大学 航空科学与工程学院,北京100191)
伴随着计算流体力学(CFD)技术的日益发展,人们对高精度格式的需求愈发强烈.譬如研究具有多尺度的湍流问题以及对一些涉及气动声学、热流、摩阻及非定常流动问题的计算,需要采用具有多维分辨能力的高阶格式才能得到较为满意的结果[1-2].
目前,CFD界对高阶格式的研究方兴未艾,ENO (Essentially Non-oscillatory)、 WENO[3](Weighted Essentially Non-Oscillatory)、ENN(Essentially Non-oscillatory,No-free-parameter)、紧致格式及谱方法等格式雨后春笋般应运而生.但它们都因为计算量过大或是鲁棒性较差而无法被广泛应用于复杂飞行器的流动模拟当中.此外,上述格式的构造思想都是基于一维插值,而实际流动是多维的,因此在计算中它们无法判断多维流动现象,特别是多维流动间断(如与网格斜交的斜激波),以致分辨率降低.为了克服这一缺陷,近十年来,国内外的学者发展了一系列基于多维流动的计算格式,比如:模化波速法、旋转通量法等[4-6].然而实践表明,这些方法虽然在计算精度方面比传统方法有显著改善,但鲁棒性较差,在多维间断处的保单调性不足,特别是在模拟高超声速时流场时,强激波附近常常产生剧烈的非物理振荡[7].另外,这些方法的求解效率较差,因而未被广泛使用.
与上述方法相比,Kim和Noh等[8-9]提出的多维限制器MLP[10]有较好的鲁棒性和收敛性,将其与传统的TVD[11]高阶插值格式相结合可以更好地抑制多维振荡.由于 Roe[12]格式是被广泛认可的空间离散方法,因此本文将结合Roe格式的MLP限制器方法与一些常用数值计算方法的计算结果进行对比,发现该多维限制器有如下优点:①相较于传统二阶TVD格式,在效率相当的情况下有更高的分辨率.②在多维间断处能够有效抑制振荡.③保证强鲁棒性及收敛性的前提下有较高的求解精度.④算法简单,容易实现.
1 计算方法
1.1 控制方程及空间离散方法
二维N-S方程(Navier-Stokes equations)的守恒形式[13]为
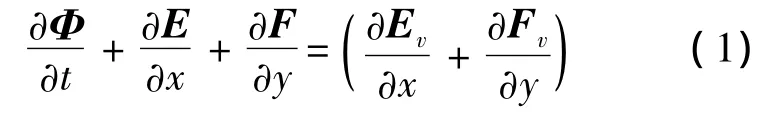
式中流通矢量为
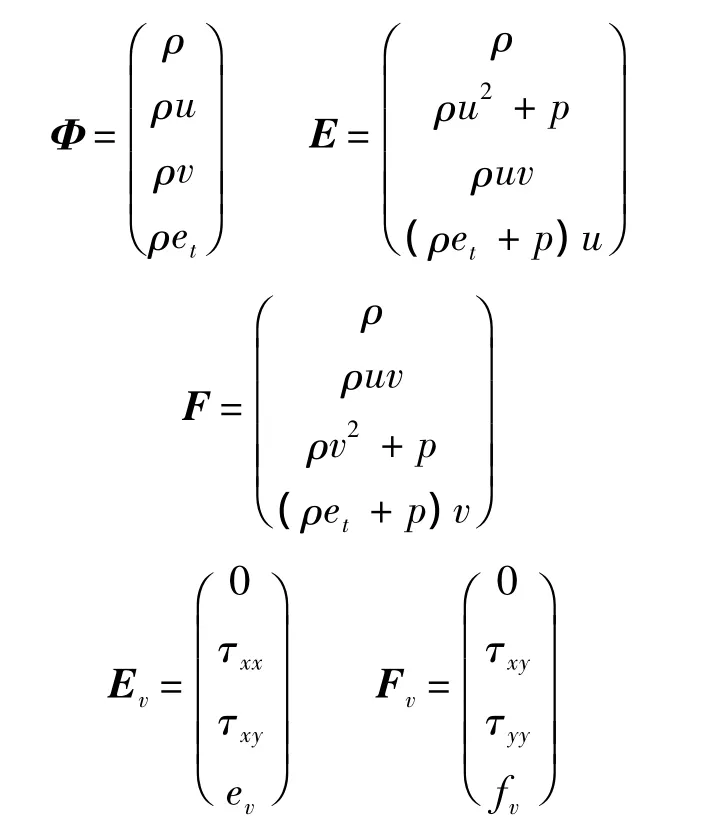
1.2 MUSCL(TVD)限制器的一般形式
MUSCL 格式的具体形式[14-15]为
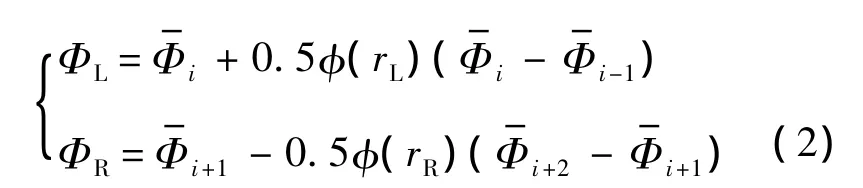
式中,φ(rL)φ(rR)为限制器;Φ表示通量矢量.
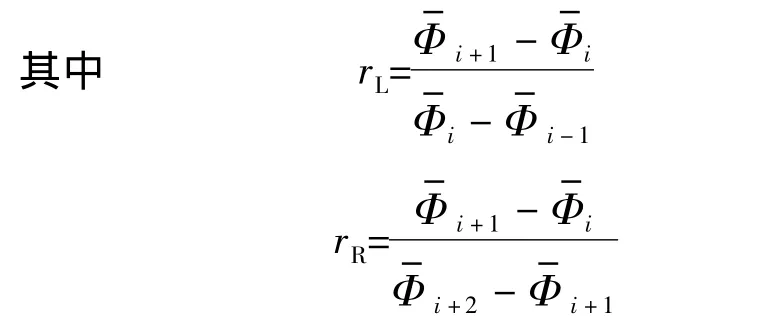
1.3 高阶多维限制器的构造
高精度多维限制器的主要构造方法如下[16].
首先构造高阶TVD插值:
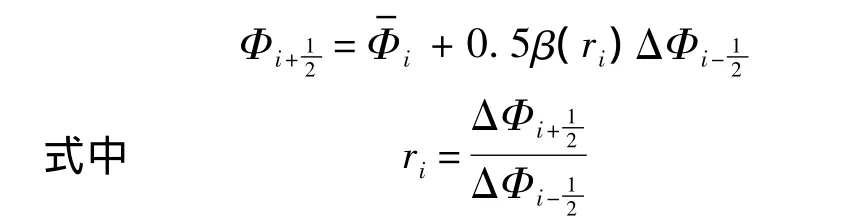
因此,为了抑制在间断处的振荡,高阶插值也应满足TVD限制条件:
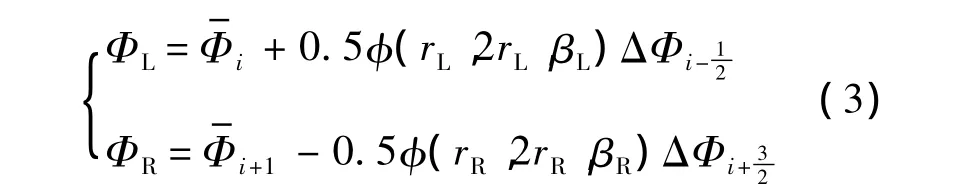
式中3阶限制器的表达形式为
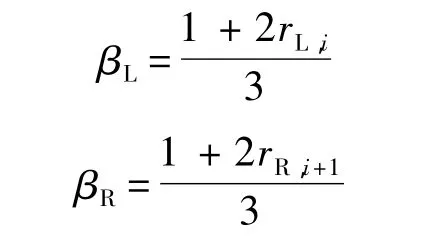
5阶限制器的表达形式为
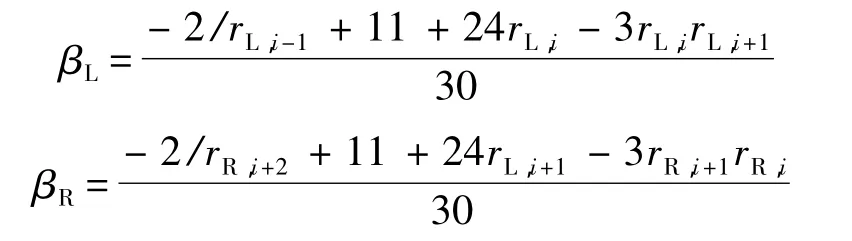
其次,构造多维限制函数,由单调性条件,界面通量函数值应在空间相邻的8个函数值范围之间,即
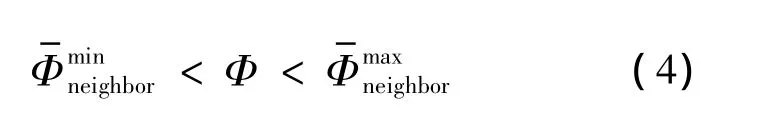
在充分考虑了4个方向(上下左右)的θj(如图1所示)后,得出多维限制条件如下:
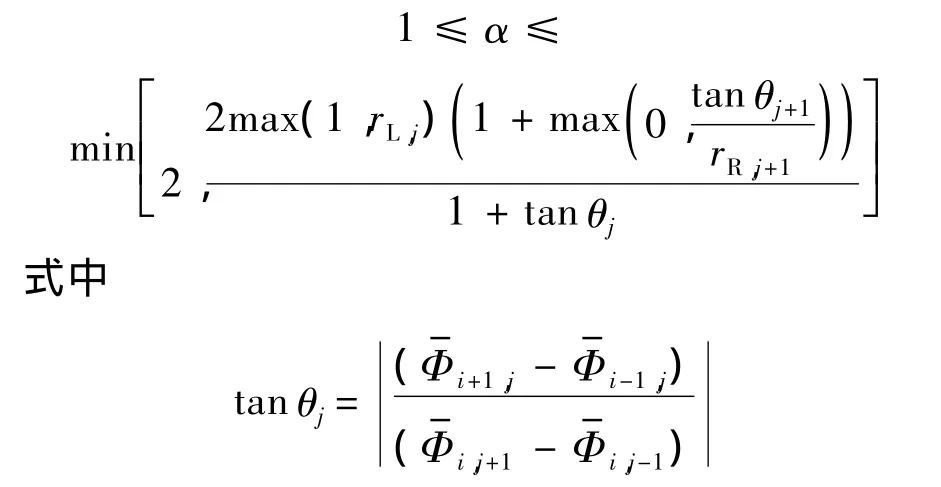
综上所述,得到高阶限制器的表述形式:
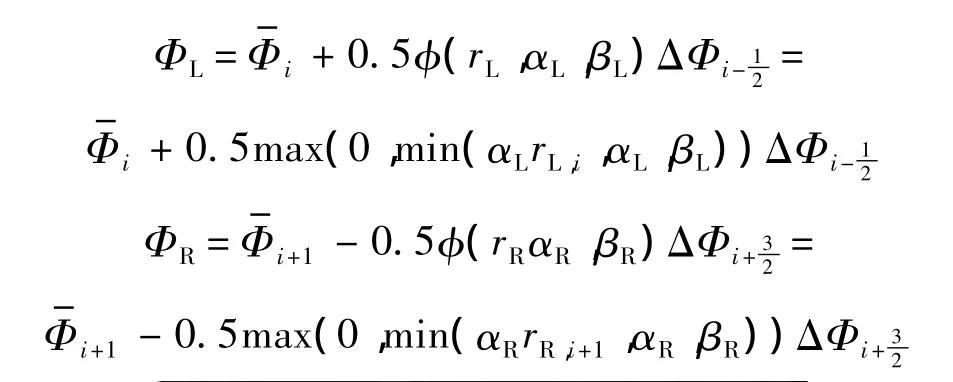
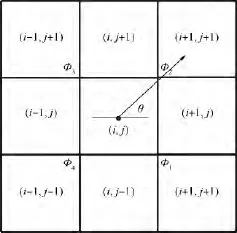
图1 格点值与格心值分布示意图Fig.1 Distribution schematic of cell-vertex value and cell-center value of grid
2 算例及结果分析
为进一步分析验证该多维限制器的性能,本文做了一系列数值实验,包含无黏非定常问题及有黏的激波边界层干扰问题.简便起见,下文算例中3阶多维限制器用MLP3表示,3阶WENO格式用WENO3表示,5阶WENO格式用WENO5表示.时间格式方面,非定常问题采用3阶龙格库塔法,定常问题采用无条件稳定的LUSGS方法.
2.1 Sod 问题
计算域为[0,1],网格点数为 100,初始条件为

计算推进到t=0.2 s中止,此时,流场中包含一个激波、一个接触间断和一个膨胀波.
比较密度分布曲线(图2)可得,minmod限制器耗散较大,WENO3格式次之,WENO5格式及MLP3限制器的分辨率较高,而局部放大图更清晰地表明了这一结论.
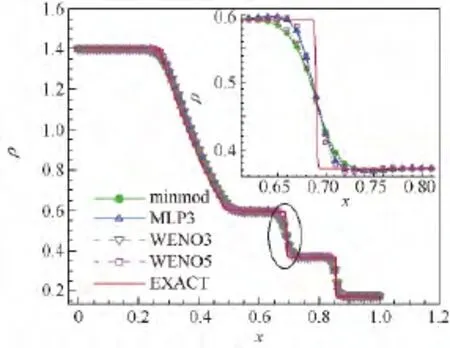
图2 密度分布曲线Fig.2 Density distribution curves
2.2 二维涡流动问题
涡流动问题是一个典型的非定常多维流动问题.初始流场是在均匀流场上添加了一个等熵涡,该涡的强度为Γ=5.计算区域为10×10的方形区域,网格点数为80×80.扰动的形式如下.

式中,γ为比热比;(x0,y0)为涡核的坐标.
理论上该无黏涡的涡核压强随着时间的推移是保持不变的.
初始流场密度分布如图3所示.图4给出了漩涡转动100个无量纲时间后,3种不同插值方法得到的沿AB线(图3)的密度分布曲线.结果表明,在多维光滑的情况下,minmod限制器有较大的耗散;与WENO3格式相比,MLP3限制器有较好的多维分辨能力.
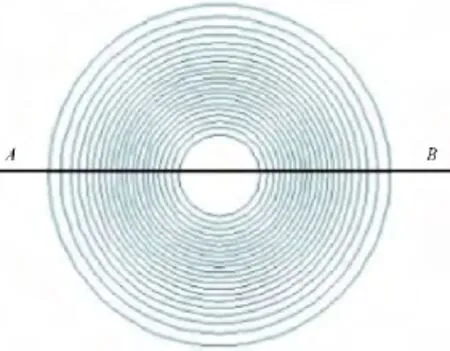
图3 初始流场密度分布Fig.3 Density distribution of initial vortex flow field
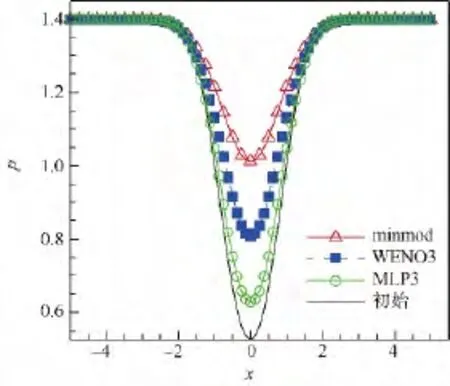
图4 沿AB线的压力分布Fig.4 Pressure distribution along line AB
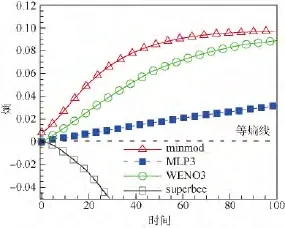
图5 熵随时间变化的曲线Fig.5 Variation curves of entropy with change of time
分析熵随时间的变化曲线(图5)可知:superbee限制器计算得到的熵值一直非物理地减小,涡量变强且无收敛趋势.而其他格式的计算结果表明:minmod限制器、WENO3及MLP3限制器的熵增依此减小,精度依此增高.
取2套不同密度的网格(40×40,100×100)并分别采用3种限制器(minmod,WENO3,MLP3)计算进行对比.图6给出了各格式在不同密度网格中计算时,涡核压强随时间推进的变化情况.从中可以看出,3种限制器的耗散性均随网格量减小有所增大,但MLP3限制器的数值耗散增加最小,网格收敛性最佳.
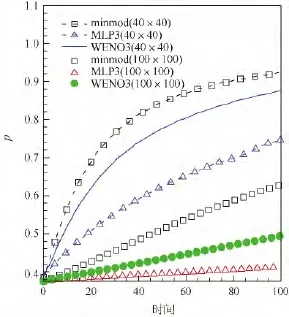
图6 不同格式的网格收敛性比较Fig.6 Comparison of grid convergence with different schemes
2.3 激波边界层干扰
本算例描述的物理问题为一斜激波入射到平板边界层上,使得边界层局部产生分离,并在平板下游再附[17].流动参数如下:Ma=2,T=117 K,Re=296000,激波与平板之间的夹角为32.598°.网格单元数是200×200.计算时CFL数取5,壁面条件为无滑移绝热壁.
图7给出了各限制器计算得到的压力等值线图,图8则给出了图7(a)所示虚线处的压强分布曲线.从中可以看出:minmod限制器及WENO3格式耗散较大;相比之下,MLP3限制器和WENO5格式可以更为清晰地分辨出入射激波及通过分离区的反射激波、膨胀扇区和再附激波等流动结构.但在图8局部放大图中,WENO5格式由于耗散过小,再附激波后出现了非物理的虚假振荡,鲁棒性较差.
图9表明MLP3限制器与WENO5格式计算所得的壁面压强分布相近,均与实验值吻合较好,较为正确地预测了分离区的大小,而其他格式的耗散较大,求得的分离区过小.
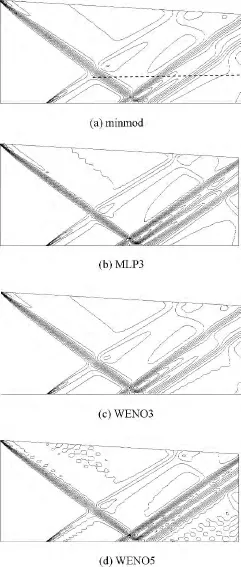
图7 压力等值线图Fig.7 Pressure contours
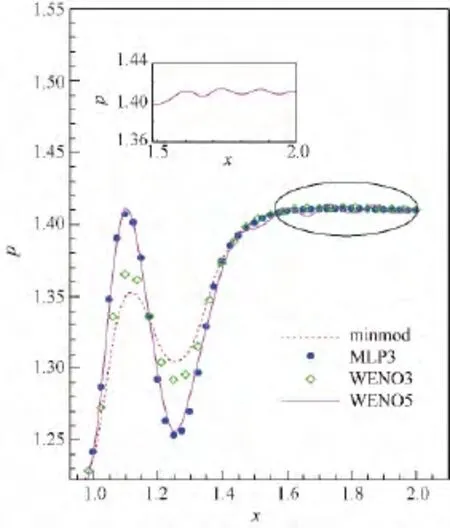
图8 压强分布曲线Fig.8 Pressure distribution curves
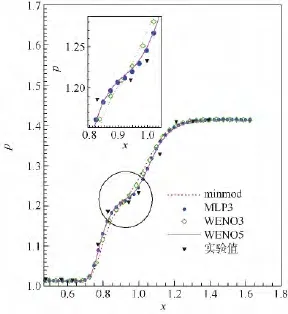
图9 壁面压强分布曲线Fig.9 Pressure distribution curves along wall surface
3 结论
本文基于无黏涡算例及激波边界层干扰等算例,研究分析了高精度多维限制器MLP3的相关特性.通过将其与传统TVD限制器及高阶WENO格式进行比较,得到主要结论如下:
1)MLP3限制器与常见二阶精度TVD限制器相比具有明显的优势:与minmod限制器相比,MLP3有较高的精度,且通过多维限制函数,它避免了过多的耗散,可以较为精确地捕捉到激波等间断;与superbee限制器相比,MLP3具有良好的保单调性以避免非物理解的产生.
2)二维涡流动算例表明:较之于高阶WENO格式及传统TVD限制器,MLP3限制器更容易实现,且在花费更小计算量的同时保持强鲁棒性及高精度.
3)激波边界层干扰算例表明:超声速有黏流动计算时,MLP3限制器的求解精度高于同阶WENO格式,与5阶WENO格式结果相似.因此MLP3具有较高的黏性分辨率和保单调特性.
References)
[1] Zhang H X.On problems to develop physical analysis in CFD[C]//Proceedings of the Fourth Asian Computational Fluid Dynamics Conference.Chengdu:IEEE,2000:3-19.
[2] 杨建龙,刘猛.限制器对高超声速表面热流数值模拟的影响[J].北京航空航天大学学报,2014,40(3):417-421.Yang J L,Liu M.Influence of limiters on numerical simulation of heating distributions for hypersonic bodies[J].Journal of Beijing University of Aeronautics and Astronautics,2014,40(3):417-421(in Chinese).
[3] Shu C W,Osher S.Efficient implementation of essentially nonoscillatory shock-capturing schemes[J].Journal of Computational Physics,1988,77(2):439-471.
[4] Roe P L.Discrete models for the numerical analysis of time-dependent multidimensional gas dynamics[J].Journal of Computational Physics,1986,63(2):458-476.
[5] Lacor C,Hirsch C.Genuinely upwind algorithms for multidimensional Euler equations[J].AIAA Journal,1992,30(1):56-63.
[6] Deconinck H,Paillere H,Struijs R,et al.Multidimensional upwind schemes based on fuctuation-splitting for systems of conservation laws[J].Computational Mechanics,1993,11(5-6):323-340.
[7] 屈峰,阎超,于剑,等,高精度激波捕捉格式的性能分析[J].北京航空航天大学学报,2014,40(8):1085-1089.Qu F,Yan C,Yu J,et al.Assessment of shock capturing methods for numerical simulations of compressible turbulence with shock waves[J].Journal of Beijing University of Aeronautics and Astronautics,2014,40(8):1085-1089(in Chinese).
[8] Kim K H,Kim C.Accurate,efficient and monotonic numerical methods for multi-dimensional compressible flows,Part II:multidimensional limiting process[J].Journal of Computational Physics,2005,208(2):570-615.
[9] Noh S J,Lee K R,Park J H O,et al.An accurate and efficient calculation of high enthalpy flows using a high order new limiting process[J].Journal of the Korean Society for Industrial and Applied Mathematics,2011,15(1):67-82.
[10] Kang H M,Kim K H,Lee D H.A new approach of a limiting process for multi-dimensional flows[J].Journal of Computational Physics,2010,229(19):7102-7128.
[11] Harten A.High resolution schemes for hyperbolic conservation laws[J].Journal of Computational Physics,1983,49(3):357-393.
[12] Roe P L.Approximate Riemann solvers,parameter vectors and difference schemes[J].Journal of Computational Physics,1981,43(2):357-372.
[13] 阎超.计算流体力学方法及应用[M].北京:北京航空航天大学出版社,2006:15-25.Yan C.Computational fluid dynamic’s methods and applications[M].Beijing:Beihang University Press,2006:15-25(in Chinese).
[14] van Leer B.Toward the ultimate conservative difference scheme[J].Journal of Computational Physics,1997,135(2):229-248.
[15] Hirsch C.Numerical computation of international and external flows:Volume 2[M].Hoboken,NJ:John Wiley& Sons Publish,1990:121-156.
[16] Park J S,Chang T K,Kim C.Higher-order multi-dimensional limiting strategy for correction procedure via reconstruction[C]//52nd Aerospace Sciences Meeting.Maryland:AIAA,2014:2014-0772.
[17] Knight D.RTO WG 10-Test cases for CFD validation of hypersonic flight,AIAA-2002-0433[R].Reston:AIAA,2002.
