基于OSN的谣言传播模型及影响力节点研究

蒙在桥，傅秀芬，陈培文，陆靖桥

（1.中山大学信息科学与技术学院，广州510006；2.广东工业大学计算机学院，广州510006）

0 引言

在线社交网络（Online Social Networks，简称OSN）的开放特性给信息交流带来便利的同时，也使得谣言、病毒等有害消息在这些平台中蔓延开来，给经济、社会都带来了许多负面影响。许多学者研究了谣言在社交网络中的传播［1－7］，期望通过有效模拟现实复杂的传播交互过程而获得有价值的机理。事实上，以谣言传播机制为基础，一些企业已经运用“社交网络病毒营销”来推广他们的产品［1］，在社交网络的谣言传播过程中找出有影响力的节点意味着能以更小的控制代价抑制谣言的传播。因此，运用可靠的模型识别有影响力的节点在理解和控制消息传播过程中显得尤为重要。

谣言是一种典型的社会现象，它可以通过感染人的信仰而重塑他人的社会观念，它的传播与传染病、计算机病毒的传播十分相似［6，8］。大多数谣言传播模型都源于经典的传染病传播模型SIS或SIR，比如Daley和Kendall于1965年提出的DK模型［9］。后来Moreno、Nekovee等［8，10］发展了DK模型，并引入了该模型在均匀网络及非均匀网络中的均场方程，使之成为了较经典的谣言传播模型（本文称之为MN模型）。考虑到传播过程中的一些实际因素，最近也出现一些较新颖的谣言传播模型，比如：Wang等［4，7，11］提出基于社会加强的谣言传播模型CSR，并对CSR模型进行了改进，加入记忆效应和接受阈值，使其更适用于移动社交网络中谣言的传播仿真；Zhao等［5，12］在SIR的基础上拓展出了一类节点Hibernators，提出基于回忆机制和遗忘机制的SIHR模型；文献［6］提出了基于潜伏节点的谣言传播模型SEIR；Zhao等［13］提出一种可变遗忘率的谣言传播模型。然而，这些模型都没有考虑网络节点间的拓扑特征差异，其理论上的一些限制条件使其较难描述大规模在线社交网络中谣言传播［5］。

随着复杂网络影响力节点研究的推进［14－15］，近期也有学者致力于研究谣言传播中的影响力节点。Borge－Holthoefer等［1－3］运用MN模型在真实网络数据仿真中发现：网络中类似“防火墙”的中心节点具有中断谣言传播的作用，而他们分析真实传播数据发现，度才是描述节点影响力较好的标量，并且指出经典的理论模型过于简单，难以描述社交网络复杂活跃模式。

现有的传播模型都较少提及消息在有向网络中的传播，在一些真实的网络（如twitter、新浪微博等）中消息的传播都是有向的，有向网络比无向网络有着更复杂的拓扑和组织结构［16］。并且，社交网络优先连接的特性导致节点之间存在较大的拓扑差异，这些差异对节点的传播影响力有重要影响［14］，现有模型都较难体现这种差异。针对传统模型的不足，本文首先在分析经典谣言传播模型及OSN活跃模式的基础上提出一种基于OSN的动态谣言传播模型（DRSIR）；然后，在真实微博网络数据下对谣言传播进行仿真，分析模型参数变化对传播的影响以验证模型的有效性；最后，本文分析节点的传播影响力与4种中心性特性间的相关性，发掘最能描述节点传播影响力的指标。

1 建模分析

1.1 MN模型及接触退化方式

MN模型［10］是谣言传播模型中较为经典的模型，它将网络节点分为3类：未知者、传播者和免疫者。当传播者接触未知者时，后者以概率λ成为传播者，当传播者接触免疫者或者其他传播者时，前者以概率α成为免疫者。当所有的传播者在接触其他个体的过程中都退化成免疫者时，传播过程终止。本文将这种传播者以接触他人而退化成免疫者的方式称为接触退化方式，目前多数的谣言传播模型都是采用接触退化方式［5－7，12，17］。

传统的传染病传播模型和MN模型都是运用平均场理论，其思想认为网络中相互作用的整体效果等价于一个“平均场”［7］，它抛开个体之间具体的细节，假设网络中所有个体都有一致的传染可能性和免疫力（或称治愈率）。在均匀网络（如ER随机网络和WS小世界网络）的传播动力学中接触退化方式和均场的假设都是合理的，因为在均匀网络中可以忽略节点之间的差异而假设网络中个体的度都等于网络平均度，传播者可以在相同接触过程中慢慢退化。但在非均匀网络中（如BA无标度网络），尤其是在有向传播的OSN中，优先连接的特性使节点度呈现出“富者愈富”的效应，节点之间存在较大的拓扑差异。

“富者”往往拥有更多的接触邻居，这种传播者接触退化方式会使其更容易退化成为免疫者。以MN模型的传播规则为例，在一个消息以广播形式传出的有向社交网络中，传播者j在变成免疫者之前的每一个时间步都将接触其所有的出度邻居，那么j在t时刻成为免疫者的概率为

为了更好描述谣言传播的退化机制，一些谣言传播模型已经开始考虑传播者自行退化的方式［5，8，13］。本文也引入一个基于传播者存活时间的退化函数使传播者自行退化成免疫者。

1.2 节点的活跃模式分析

经验的数据分析表明［2，18］，OSN中的用户都呈现出复杂多样化的活跃模式，谣言在社交网络中的传播也是一个复杂的社会心理过程［8］。结合OSN的特点，本文对用户的活跃模式做了分析：

1）在OSN中，用户并不一直都能保持活跃在线，只有在线的用户才能接收到消息。用户即使在线，也可能需要一定时间来接受消息中的思想并作出响应［19］。为了模拟OSN中的这种在线行为，本文引用文献［20］中登录概率的思想，引入在线概率θ，即用户在线并且已读取消息的概率。换句话说，θ即为传播者与其邻居未知者的接触概率，它也反映社交网络中用户的整体在线活跃度。

2）未知者在线收到消息后，将根据对消息内容的兴趣以及自身意愿进行传播，不同的用户都会对消息都会有不同的接受或抵制程度。在微博社交网络中，许多用户接收到了一条消息，但愿意转发而使其传播的可能性很小［2］，且不同用户的转发可能性都不同，通常粉丝量越多的用户越不轻易转发可疑消息。因此，我们认为谣言传播模型中不同的节点应赋予不同的免疫力。

3）直观上来说，具有更高权威度的文档消息往往会更有可能引入更多的原创内容［21］，那么谣言经由较高权威度的传播者传出往往具有更高的可信度，也更可能被传播。因此，我们认为模型应该赋予用户不同的权威度。而且在社交网络中，接收更多来自邻居传来的增强信号可以使用户更愿意接受某个行为［22］，信号的次数和传播者的权重是未知者做判断的重要依据［7］。因此本文在构建传播模型时考虑增强信号的效应。

2 DRSIR模型

一个合适的传播模型除了需要准确合理地描述社交网络中的谣言传播过程外，还需要一个激发个体参与谣言传播的各种行为机制的定量函数［8］。结合上面对社交网络传播机制的分析，本文尝试性地提出基于OSN的动态谣言传播模型。该模型考虑n个节点的有向社交网络G＝（V，E），网络的节点集合V是指社交网络中的用户，E表示用户节点间传播关系的有向边集合。定义网络中节点有3种状态：未知者、传播者和免疫者。未知者是指未接收到谣言的用户，传播者是指传播谣言的用户，免疫者是指收到谣言后对谣言不感兴趣或者传播者经过一段时间后失去传播可能性的用户。将消息每一个时间片的传播过程分为2个阶段：

1）网络中的传播者s将消息传出，其出度邻居中在线的未知者以在线概率θ接收该消息，每个传播者记录存活时间ts，并根据一个退化函数η（ts）自发地退化成免疫者。

2）在线的未知者i接收到该消息后，将以概率pis（i）成为传播者，否则成为免疫者。pis（i）的值根据i的免疫能力、接收消息的次数和传播者的权威度综合计算。

2.1 传播者退化机制

本文将传统的传播者接触式退化方式改为基于传播者存活时间的自发退化方式，并引用修改的Parato分布函数［23］作为节点的退化概率函数：

其中，ts≥1为传播者的存活时间，即节点处于传播者时经历的时间片数量，α＞1，tmin≥1作为参数决定了函数的形状。从图1中可以看出：退化概率η（ts）随着ts的增加而增大；在固定tmin时，参数α的值越大，η（ts）上升的速率越快，该参数可以视为是传播节点的退化速率，反映用户发出的消息被其他消息所掩盖的速度；固定α增大tmin时函数图像向右平移，因此tmin定义为传播者存活时间的最小值，即传播者在经历了tmin个时间片时才开始退化。运用该函数可以较灵活地调节传播者的最小存活时间及退化速率。不失一般性，在本文实验中都取tmin的最小值1。

2.2 动态的感染概率

经验的数据分析指出，社交网络中用户的活跃度分布与度分布相关［2，18］。本文定义da（i），dr（i）分别为节点i的权威度和免疫力，两者值相同且根据节点出度大小动态指定，都服从出度相关的对数函数：

其中，ajs（i）为i的入度邻居传播者集合。最后可定义未知者接收谣言后成为传播者的概率pis（i）：

其中，在线概率θ是与网络活跃度相关的，而λ则是一个与网络无关的用于衡量谣言本身影响力的参数，称之为谣言的传播率。

2.3 DRSIR的仿真传播过程

DRSIR的传播仿真过程是基于离散的时间模型，在每个时间片内，所有传播者向其出度用户广播消息，未知者则根据在线概率、消息影响强度以及自己的免疫力等因素转换状态。当未知者以概率θ在线时，表示该用户查阅了该消息，并将会以概率成为传播者，或者以概率成为免疫者。离线的未知者将不改变状态，并在每个时间片结束前将δ（i）置0，这样可以有效防止消息的接触冗余［25］。每一个时间片，传播者将根据自发退化机制逐渐退化成免疫者，存活的传播者将在下个时间片继续影响传播。迭代上述过程直至网络中的传播者数量为0，则整个传播过程结束。因此，传播结束时免疫者的数量可反映谣言传播的范围，传播者数量的最大值可反映参与传播的人数，迭代的次数即是时间片的数量，可以反映传播时间。模型的角色状态转移过程如图2所示。

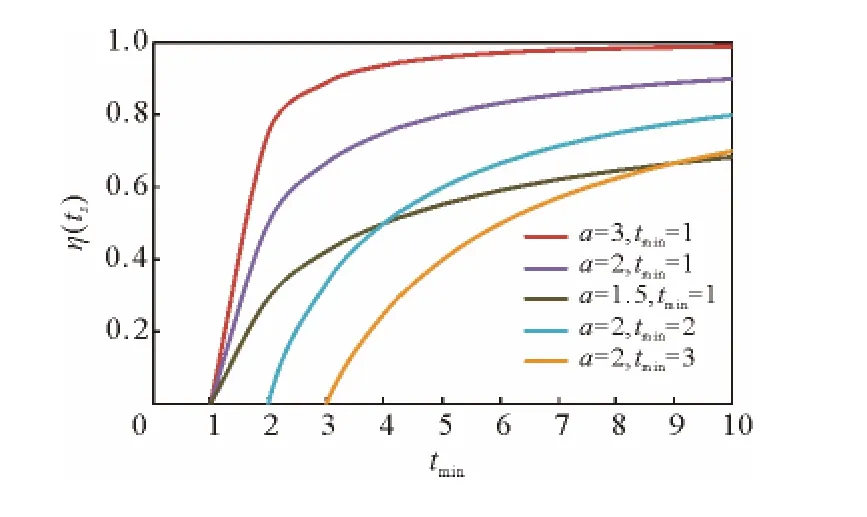
图1 参数α、tmin变化时退化函数的变化Fig.1 Annihilation function over time with different values ofαand tmin

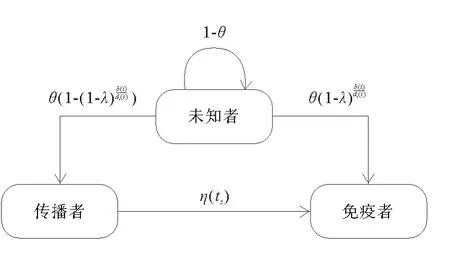
图2 DRSIR仿真传播过程中的状态转移Fig.2 State transition of DRSIR rumor spreading process

初始时所有节点的状态都为未知者，根据相应选择策略将I（I≪n）个节点的状态设为传播者作为谣言的初始传播源，然后根据上述状态转移规则迭代演化直至网络中没有传播者时传播结束。整个仿真过程就是通过3种角色的转换来描述谣言的传播过程，记录传播结束时免疫者的密度RS、传播过程中传播者密度的最大值MaxIS以及传播结束时迭代次数It作为仿真传播的评估量。

在OSN中，一条消息可以在很短的时间内引爆并影响人对事物的认知，尤其是谣言、病毒或者动乱等消息的迅速扩散会给经济和社会带来巨大的影响。识别复杂网络中有较高影响力节点具有重要意义，不仅可以通过抑制这些节点而控制谣言或者不良舆论的传播以减小对社会稳定带来的影响；还可以合理利用这些节点来确保最有效地使用网络资源，使消息得以更快更广的传播。本文运用DRSIR消息传播模型在真实的有向传播网络进行传播仿真，对网络中的度、紧密中心性［26－27］、介数中心性［28］以及k－核中心性［29］指标进行传播的相关性分析，本节简要介绍复杂网络的紧密中心性、介数中心性以及k－核中心性3个中心性指标及其在有向网络中的计算方法。

3 评估与应用

3.1 数据集描述

新浪微博是一个消息有向传播的OSN，且具有无标度和小世界的网络特性，其节点的度服从幂律分布［30］。我们运用自己编写的网络爬虫，分别从本文作者、姚晨以及某条微博的转发用户出发，逐层爬取传播网络数据。首先从初始用户出发爬取三层以内的粉丝及关注关系，然后将爬取的用户作为网络的节点、粉丝及关注关系作为网络的边，最终构成了本文所需的3个网络数据集，其基本特征如表1所示。

从表1中描述的平均路径长度、网络直径、平均聚类系数可以看出，3种方式爬取微博网络的基本特征无太大差异，皆符合小世界网络的特征。

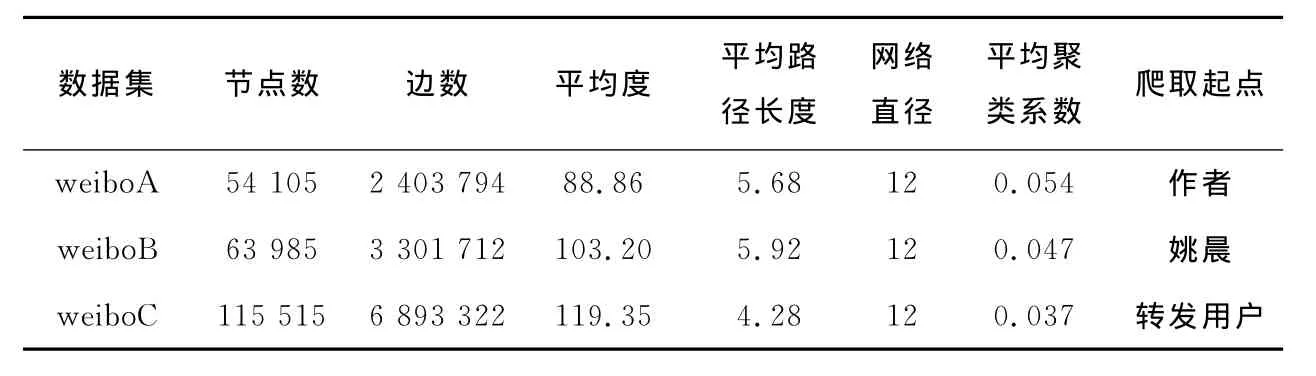
表1 3个真实网络的基本拓扑特征Tab.1 The basic topological features of the three real networks

3.2 谣言传播仿真

为验证模型的有效性，本文根据DRSIR模型编写了仿真程序，并对真实社交网络做了大量的传播仿真实验以研究模型参数α，θ以及λ对谣言传播产生的影响。选择出度最大的10个用户作为消息的初始传播源，并重复仿真运行20次以求取平均结果，下面对weiboB网络的仿真结果进行分析。

图3显示了固定其他参数，退化速率α变化时传播的变化情况。可以看出，随着退化速率的增大，传播结束时的迭代次数下降，意味着谣言传播过程也越快结束（见图3a），图3b中的RS，maxIS也随之略微下降，当α值大于2.7时传播效果趋于稳定，说明传播者退化得越慢，消息可以传播得越久越广。这个现象说明传播的延迟会对传播造成影响［31］，事实上，谣言被其他消息淹没的速度越快，其能够影响的人群就越小，但由于OSN中消息的响应速度较快，这个影响能力并不大。

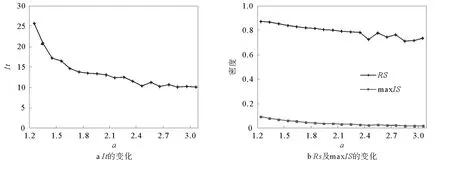
图3 传播结果随α的变化Fig.3 The simulative spreading results overα

图4为在线概率θ以及谣言传播率λ变化时仿真传播的变化情况。图4a中可以看出，谣言传播的范围RS及传播者数量MaxIS都随着θ值的增加而上升。图4b中也显示了随着λ增大，RS及MaxIS也都随之增大。这些现象都可以合理地作出解释：在线概率θ越高意味着OSN中的用户越活跃，显然谣言也比较容易扩散出去；而谣言传播率λ越大意味着谣言的影响力越大，未知者越容易被影响而变为传播者，该谣言也越容易在网络中普遍传播。

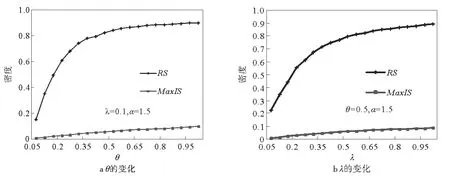
图4 传播结果随θ及λ的变化Fig.4 The simulative spreading results overθandλ

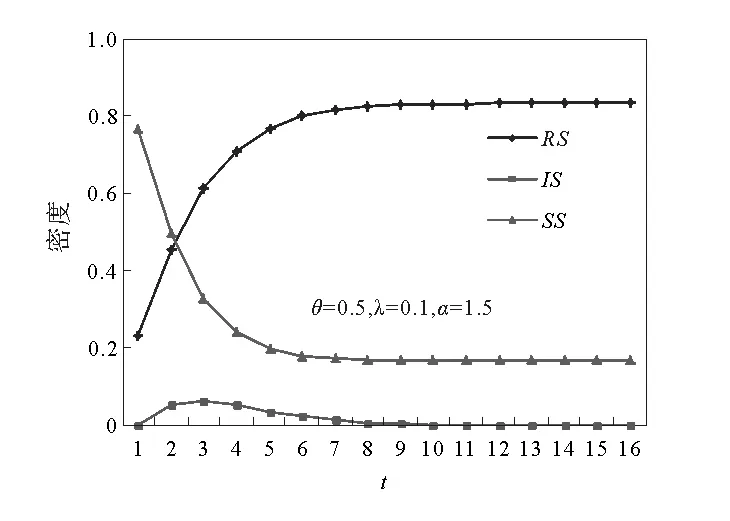
图5 DRSIR模型的仿真传播过程Fig.5 Simulative spreading process of DRSIR

图5显示了仿真过程中未知者密度SS、传播者密度IS以及免疫者密度RS随着时间的变化。可以看出该传播过程符合真实传播中急剧上升再缓慢结束的特征，最终传播者数量为0并到达稳态。说明代表不同物理意义的参数变化时，仿真传播过程能较好反应现实的传播变化过程。

3.3 影响力节点识别

为了识别谣言传播过程中有较高影响力的节点，本文依次设定每一个节点作为单个的初始传播节点，用DRSIR模型模拟谣言传播过程并记录传播结束时免疫者的密度RS。为获得可靠的实验结果，对每个节点重复仿真20次，并记录所有RS的平均值作为节点的传播影响力。那么单个节点的平均传播影响力可表示为

RSi，m代表以节点i作为初始传播者，第m次仿真传播时免疫者的密度。那么节点不同k－核值下的传播影响力可以用Mkc值［1］衡量：

其中，γkc表示k－核值为kc的Nkc个节点的集合。再根据每个节点的RSi值，计算在粗粒度下的平均免疫者密度

其中，c为CC、CB和kc当中的一种标量，γc，kout为在（c，kout）的粒度区间内的节点集合，而Nc，kout则为在该区间内的节点数量。Mc，kout的值代表了在（c，kout）粒度区间内节点的平均传播影响力。

然后，根据式（7）本文统计了的3个数据集在不同核数下的传播影响力（见图6）。从图6a和图6c中可以看出，在weiboA和weiboC网络中Mkc值随着核数增大而呈现出上升的趋势。然而，在图6b的weiboB网络中，虽然核数前段部分核值慢慢增加时Mkc随之增加，但后面的Mkc值随核值增大反而有下降的趋势。这个现象与文［14］和文［1］中的实验结果都有所差异：文［14］中认为最有影响力传播者可以用k－核值识别，而文［1］的仿真中发现k－核值的大小对传播无影响。

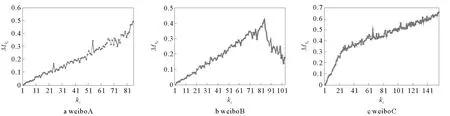
图6 不同核数节点传播源下的平均免疫者密度Fig.6 Average stifler density for rumor processes initiated at nodes with coreness kc

最后，为了衡量节点传播影响力与中心性特征之间的相关性，根据公式（8）统计了在不同中心性特征对比下的Mc，kout值，结果如图7所示。其中，各子图中小方格的不同颜色代表了不同的Mc，kout值大小，即该粒度区间内节点的平均免疫者的密度。图7（a，d，g）、图7（b，e，h）和图7（c，f，i）分别对比了节点在（CB，kout）、（CC，kout）和（kc，kout）的组合粒度区间下的平均免疫者的密度。图中可以看出，整体上3个网络在拓扑特征对比下的节点分布形状无太大差异，说明3个网络的拓扑结构相似。在各子图中的Mc，kout值都随着kout的增大而呈现层次性地增大，在图7（b，e，h）中CC的值也与Mc，kout值正向同步，而CB和kc的变化却都不能很好描述Mc，kout值的颜色变化，说明kout和CC相对来说能更好地描述节点传播影响力。图7（c，f，i）中可以发现一些高核数的节点传播影响力较低，且这些节点的出度都较小，有的甚至小于核数。网络中节点的入度只能体现消息的流入可能性而不能体现输出可能性，weiboB中有较多高核节点仅仅入度较高，而核数是由节点的出度与入度之和决定，这就导致weiboB中有些高核数节点传播影响力较低。因此k－核并不适合描述有向网络中的节点的传播影响力。从图7（b，e，h）中可以看出，3个网络中出度和紧密中心性具有较高的正相关性，这两个指标都可以较好地描述节点的传播影响力，但一般在OSN中度值可以较容易获得，而由于网络规模及计算复杂性，紧密中心性的计算是十分困难的。

图7 出度与其他3个中心性特征对比下的平均免疫者密度Fig.7 Average stifler density on the comparison of outdegree and other three centrality features

4 结论

本文结合社交网络谣言传播过程中一些实际因素：网络在线活跃性、传播者自发退化方式、节点间差异等，提出一个基于OSN的谣言传播模型，该模型的主要特点有：1）采用基于时间退化函数的传播者退化方式，弥补接触退化的不足；2）考虑了网络节点间的拓扑差异，动态指定节点的权威度和免疫力；3）考虑了传播的接收增强信号效应。在真实网络数据下，该模型的仿真结果能显现真实OSN中的传播情形。仿真结果还发现，在有向OSN中k－核并不能有效识别有影响力的节点。原因是k－核分解综合考虑了节点的出度和入度，一些高核数节点仅仅入度较高而无法提升消息的输出可能性。而出度和紧密中心性这两个特征皆能直接反映节点到达其他节点的能力，它们都可以较好识别网络中的影响力节点。

［1］ Borge－Holthoefer J，Moreno Y.Absence of influential spreaders in rumor dynamics［J］.Physical Review E，2012，85（2）：026116.

［2］ Borge－Holthoefer J，Meloni S，Gon？alves B，et al.Emergence of influential spreaders in modified rumor models［J］.Journal of Statistical Physics，2012：1－11.

［3］ Borge－Holthoefer J，Rivero A，Moreno Y.Locating privileged spreaders on an online social network［J］.Physical Review E，2012，85（6）：066123.

［4］ Wang H，Deng L，Xie F，et al.A new rumor propagation model on SNS structure［C］／／2012IEEE International Conference on Granular Computing.Hangzhou，China，2012：499－503.

［5］ Zhao L，Wang J，Chen Y，et al.SIHR rumor spreading model in social networks［J］.Physica A，2012，391（7）：2444－2453.

［6］ 顾亦然，夏玲玲.在线社交网络中谣言的传播与抑制［J］.物理学报，2012，61（23）：544－550.Gu Yiran，Xia Lingling.The propagation and inhibition of rumors in online social network［J］.Acta Physica Sinica，2012，61（23）：544－550.

［7］ 王辉，韩江洪，邓林，等.基于移动社交网络的谣言传播动力学研究［J］.物理学报，2013，62（11）：96－107.Wang Hui，Han Jianghong，Deng Lin，et al.Dynamics of rumor spreading in mobile social networks［J］.Acta Physica Sinica，2013，62（11）：96－107.

［8］ Nekovee M，Moreno Y，Bianconi G，et al.Theory of rumour spreading in complex social networks［J］.Physica A，2007，374（1）：457－470.

［9］ Daley D J，Kendall D G.Epidemics and rumours［J］.Nature，1964，204：1118.

［10］Moreno Y，Nekovee M，Pacheco A F.Dynamics of rumor spreading in complex networks［J］.Physical Review E，2004，69（6）：066130.

［11］Wang H，Deng L，Huang Y S，et al.A variant epidemic propogation model suitable for rumor spreading in online social network［C］／／The 2012 International Conference on Machine Learning and Cybernetics.Xi′an，China，2012：1258－1262.

［12］Zhao L，Qiu X，Wang X，et al.Rumor spreading model considering forgetting and remembering mechanisms in inhomogeneous networks［J］.Physica A，2012，392：987－994.

［13］Zhao L，Xie W，Gao H O，et al.A rumor spreading model with variable forgetting rate［J］.Physica A，2013，392（23）：6146－6154.

［14］Kitsak M，Gallos L K，Havlin S，et al.Identification of influential spreaders in complex networks［J］.Nature Physics，2010，6（11）：888－893.

［15］Chen D，LüL，Shang M－S，et al.Identifying influential nodes in complex networks［J］.Physica A，2012，391（4）：1777－1787.

［16］Dorogovtsev S N，Goltsev A V，Mendes J F.Critical phenomena in complex networks［J］.Reviews of Modern Physics，2008，80（4）：1275－1354.

［17］Ya－Qi W，Xiao－Yuan Y，Yi－Liang H，et al.Rumor spreading model with trust mechanism in complex social networks［J］.Communications in Theoretical Physics，2013，59（4）：510.

［18］Perra N，Gonçalves B，Pastor－Satorras R，et al.Activity driven modeling of time varying networks［J］.Science Report，2012，2：469.

［19］Jin F，Dougherty E，Saraf P，et al.Epidemiological modeling of news and rumors on twitter［C］／／The 7th Workshop on Social Network Mining and Analysis，Chicago，United States，2013：8.

［20］和亮，冯登国，王蕊，等.基于 MapReduce的大规模在线社交网络蠕虫仿真［J］.软件学报，2013，24（7）：1666－1682.He Liang，Feng Dengguo，Wang Rui，et al.Mapreduce－based large－scale online social network worm simulation［J］.Journal of Software，2013，24（7）：1666－1682.

［21］Lin C X，Mei Q，Han J，et al.The joint inference of topic diffusion and evolution in social communities［C］／／The 11th ICDM.Vancouver，BC，Canada，2011：378－387.

［22］Centola D.The spread of behavior in an online social network experiment［J］.Science，2010，329（5996）：1194－1197.

［23］Newman M E.Power laws，Pareto distributions and Zipf＇s law［J］.Contemporary Physics，2005，46（5）：323－351.

［24］González－Bailón S，Borge－Holthoefer J，Rivero A，et al.The dynamics of protest recruitment through an online network［J］.Science Report，2011，1：197.

［25］LüL，Chen D B，Zhou T.The small world yields the most effective information spreading［J］.New Journal of Physics，2011，13（12）：123005.

［26］Newman M.The mathematics of networks［J］.The New Palgrave Encyclopedia of Economics，2008，2：1－12.

［27］Costenbader E，Valente T W.The stability of centrality measures when networks are sampled［J］.Social Networks，2003，25（4）：283－307.

［28］Brandes U.A faster algorithm for betweenness centrality［J］.Journal of Mathematical Sociology，2001，25（2）：163－177.

［29］Dorogovtsev S N，Goltsev A V，Mendes J F.k－Core organization of complex networks［J］.Physical Review Letters，2006，96（4）：040601.

［30］苑卫国，刘云，程军军，等.微博双向“关注”网络节点中心性及传播影响力的分析［J］.物理学报，2013，62（3）：494－503.Yuan Weiguo，Liu Yun，Cheng Junjun，et al.Empirical analysis of microblog centrality and spread influence based on bi－directional connection［J］.Acta Physica Sinica，2013，62（3）：494－503.

［31］Xu X J，Chen G.The SIS model with time delay on complex networks［J］.International Journal of Bifurcation and Chaos，2009，19（2）：623－628.