延迟预警对家庭网络早期传播行为的影响

刘 芳，许小媛，郑 义

（1.江苏开放大学，南京210036；2.南京邮电大学，南京210023）

0 引言

信息的扩散随着通讯技术的飞速发展而变得快捷，现代社会的个体，不论是Internet网络的使用者，还是SARS，禽流感等流行性病毒爆发过程中的人类个体，都更容易获得有关蠕虫病毒或疾病的预警信息。在获知预警信息情况下，个体会采取相应的防护措施，从而影响病毒的传播动力学进程。预警机制以及由此产生的人类行为，对传播动力学的影响获得了广泛关注和研究［1－6］。依据预警信息的来源，可分为全局预警与本地预警，全局预警对应现实中官方机构使用广播、电视、报纸、网络等手段进行的全局范围的通知；本地预警则对应现实中个体通过接触、交流获知的本地邻居中的警示信息。预警信息一旦产生并传播，网络结构中即存在两个传播过程，即信息的传播与病毒的传播。为了反映现实世界的不同情况，相关研究又分为两类：预警信息流行度依赖于病毒流行程度［2，5］；预警信息的流行与病毒的传播过程相互独立［6］。前者为基于流行程度的模型，反映的是个体依靠获知染病个体的比例，从而判断病毒的流行与严重程度，进而升级或减少防护行为；后者基于信任建模，即个体不考虑病毒流行程度，以事先假设的概率对接收到的预警信息进行判断、采纳与继续传播。

预警机制研究中，网络拓扑对动力学行为的影响是不可忽略的，交叉覆盖网络［7］，无标度网络［5，7］，家庭（社团，群组等，以下均记为家庭）网络［8］均得到了关注。文献［8］对基于双层混合假设的家庭网络的早期干预行为进行了研究，并对早期干预措施的延迟（包括常数和指数分布延迟）对传播进程的影响进行了分析仿真，将其分析模型应用于2009年H1N1流感数据，得到了基于药物的早期干预措施只有在病毒爆发的第一个24小时内具有遏制有效性的结论，其方法具有计算高效的特点。

在基于流行程度的预警机制研究中，节点的风险意识随着本地和全局的预警信息量成指数变化，而本地预警信息量正比于染病邻居数与节点总邻居数的比值，全局预警信息量正比于网络全体染病个体与总人口的比率［2，5］。文献［2－5］专注于传播阈值研究，使用节点脆弱性指标来捕捉预警机制的动力学影响，随着预警信息量增大，节点脆弱性下降。染病个体与健康个体一次接触的传播成功率设定为染病个体传播率与健康个体脆弱性的乘积。文献［4］对全局预警、本地预警与接触过程进行了综合考虑，提出了流行程度和预警信息接触次数两种建模因素，其研究发现，不同于本地预警和接触预警，全局预警并不影响传播阈值。与文献［2－5］专注于传播阈值分析不同，本文将研究重点集中于早期传播动力行为，具体在双层混合结构的家庭网络上，专注于对基本家庭复制数，双倍复制时间等指标的计算与分析。

在双层混合网络结构上，考虑预警感知的动力学行为的相关文献还较少。文献［8］专注于早期干预行为的时间有效性研究，对干预机制简化设定为传播率与脆弱性分别下降为干预前的（1－τ）与（1－ρ），其中τ，ρ∈（0，1）且为常数。我们利用其分段马尔科夫链路径积分计算方法［8－9］，综合考虑了家庭网络上全局预警与本地预警，对全局预警和本地预警的延迟敏感性进行了对比分析。

1 传播模型

基于双层混合假设的家庭网络其基本模型如下［10］：从网络结构角度，将系统划分为多群组结构，网络中节点既属于全局网络，也属于某个规模上小得多的特定的家庭，其既与全局范围内的其他家庭成员发生弱交互行为，同时又与本地家庭成员存在强交互行为，且节点接触率在家庭内比在家庭间高得多。双层混合结构可以视为数学易求解性与真实网络结构复杂性的一种折中［11］。

对疾病、蠕虫病毒以及谣言的传播行为进行数学建模研究，已经具有较长的历史，并根据其在传播过程中的不同侧重得到了多种数学模型。在我们工作中，使用SEIR模型进行分析，在种群空间封闭且均匀混合的假设下，将个体依其传播状态划分为S（Susceptible，健康易染状态）、E（Exposed，潜伏）、I（Infected，感染状态）和 R（Removed，移除状态，包括免疫、死亡、隔离等多种因素）4个子种群空间，模型如表1所示。

表1 家庭网络SEIR模型Tab.1 The SEIR model of household networks

其中，k为家庭规模，δk为规模为k的家庭中成员的脆弱性参数，λL为家庭内传播率，λG为家庭间传播率，γ为康复率，σ为发病率，p（k）为规模为k的家庭在全局网络中所占比例，f为病 毒 流 行 程 度，f ＝为当前t时刻规模为k的家庭中处于感染状态成员的数目。

从传播率与脆弱性参数两方面考虑预警效应，当节点接收预警后，不论是来自本地、全局还是两者都有，染病个体的群间与群内传播率分别变为（1－τ）λG和（1－τ）λL，健康个体的脆弱性参数则变化为

其中，本地预警效应引起的节点脆弱性变化为δLk，全局预警引起的脆弱性变化为δGk，设节点初始脆弱性为1。脆弱性表示健康节点在受到传染接触时，自身免疫力决定的易感染程度，脆弱性下降对应节点感知预警后采取防护措施导致被感染变难的情况。β为个体采纳一次本地警示信息后，采取防护行为（个体防护，减少接触等）对脆弱性的降低程度（0＜β＜1）。健康节点以当前时刻家庭内染病节点的比例I（t）／（k－1）为概率来选择采纳本地预警。α（0＜α＜1）为个体对本地预警信息多次接触导致的防护加强效应。接触频率效应（k－1）－α项设计主要基于两个假设：对家庭内接触，个体i一个时步内会与家庭内所有其他成员发生接触，当家庭出现染病个体时，成员间的警示不仅由染病个体发出，也会由健康个体传递，故个体i会接收到k－1次提醒；对家庭间接触，尽管理论上假设个体i与家庭外所有成员均以较小概率发生接触，但现实中在一个时步内，个体只会与其中很小一部分发生接触，故外部交互行为可视为家庭在外部所有染病个体集合作用下的一次状态变化（S，E→S－1，E＋1），因此δGk中不出现多次接触效应项。此设定与文献［2－3］中的一般性假设相符，即个体接收到来自全局的预警信息时，倾向于将其看成是一个信息片。

在我们工作中发现，如果全局预警信息以概率f被节点采纳，f为全局染病率，即用式（2）中fρ项表示全局预警效应，则节点的脆弱性指标δGk对早期动力学指标，如家庭基本复制数、早期增长率等的影响近似为零。家庭复制数是拥有一个初始染病个体的家庭，从初始时刻到其内部病毒传播过程完全结束的时间段里，所有染病个体对其它健康家庭的家庭成功传播数。因为家庭模型的理想假设是家庭成员数有限，全局家庭数无穷大。因此，在早期种子家庭的病毒传播寿命里，f值变化很小。文献［5］亦指出，基于流行程度的全局预警对传播阈值，病毒爆发率没有影响。因此我们使用了与流行程度无关，脆弱性变化参数ρ（0＜ρ＜1）固定不变的全局预警模型，对应现实中权威机构预警通知的情况。由此，我们的工作集中于固定不变的全局预警与基于本地流行程度动态变化的本地预警对延迟的动力学敏感性分析。

2 数学计算

在早期家庭网络的传播动力学研究中，Ball等［10］提出了双层混合网络模型，来研究现实世界以家庭为单位的疾病传播行为。文献［12］在Ball等的基础上，研究了这类网络的SIS传播模型基于马尔科夫链的计算方法，得到

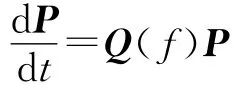
其中，Q＝（qij，i，j∈S）为马尔可夫链状态转移矩阵，P＝（P1，…，Pn）T为社团中拥有n个感染者的状态演化向量。

Ross等将上述方法拓展到SIRS模型（式（4）），并在文献［13］的马尔科夫链路径积分方法基础上（式（5）），得到了家庭基本复制数R＊（式（6））和早期增长率φ（式（7））的计算式：

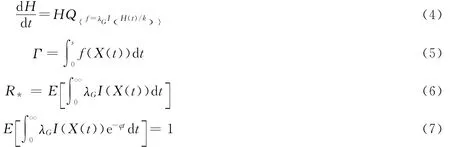
其中，基本复制数R＊考虑的是拥有一个初始传播个体的家庭在其传播寿命里对健康家庭的感染家庭数，双倍时间Td定义为系统从初始染病个体数增加一倍感染者所需时间［8］，φ为早期增长率，Td＝ln（2）／φ。

受文献［8］对马尔科夫链路径积分分段处理方法启发，本文对考虑预警延迟因素的R＊和早期增长率φ的计算分别为

由家庭基本复制数的定义可知，考察预警影响家庭m0感染健康家庭mj的效果时，预警效应是只施加在m0的动力学过程中的，本地预警源于本地流行程度，因此只与m0有关；而全局预警效果也只存在于m0中，则基于如下假设：在传播早期，全局性的干预（如预防药物发放，隔绝等）出于成本或社会、经济负面影响的考虑，在疾病大范围流行之前，只会施加在发现病例的家庭，公司或社团等局部网络。我们的模型也很容易应用于全局预警作用于所有家庭的情况，此时c2（X2（t））＝（1－τ）（1－ρ）λGI（X2（t）），I（X2（t））的求解同上。

通过设定δk构成和延迟时间分布，可以比较本地预警和全局预警的动力学影响及其延迟敏感性，在数值结果部分进一步分析。

3 数值结果

我们将延迟分两种来考虑：即全局预警延迟和本地预警延迟。借鉴文献［8］的设定方法，两种延迟均存在前后阶段，从接触到采纳预警信息为第一阶段，使用值为1的常数延迟；获得预警后到采取防护为第二阶段，使用均值为T的指数延迟，其中T∈［0，5］。除特别指出，一般参数均设为家庭规模k＝5，发病率σ＝1，康复率γ＝1，家庭间传播率λG＝1，家庭内传播率λL＝2，接触频率影响因子α＝0.2。

图1研究仅存在本地预警时的早期动力行为变化规律，设τ＝0，ρ＝0。在T∈［1，3］区间比较3条曲线，可以看出，尽管本地预警效应是基于病毒流行程度的，而早期流行程度值较低，本地预警依然对R＊和Td拥有较明显的影响作用。我们认为这是由家庭模型的人口有限性造成的。值得指出的是，在T∈［5，6］区间，β＝0曲线趋于平缓而β≠0的两条曲线依然存在坡度，表明基于流行程度的本地预警效应在此时依然发挥作用，对延迟的敏感性低于预警效应取常数值的情况（β＝0时，δLk＝k－α为常数）。

为了对图1中表现出的两种现象以及我们的分析猜想进行验证，对图1的模型进行了改变，以探讨引起兴趣的两点：家庭规模有限与延迟敏感性。图2首先将网络结构变化到复杂的真实世界的家庭规模分布，星号线、加号线、菱形线分别对应2001年英国、2003年印度尼西亚与1990年苏丹家庭规模分布［8］。接着，尝试比较常数取值的全局预警与基于流行程度的本地预警的延迟敏感性，设α＝0，即不考虑接触频率因素，τ＝0.5，ρ＝0.5，虚线与实线分别对应β＝0（即不考虑流行程度引起的动态变化）和β＝0.5（考虑流行程度）。图2可以看出，只考虑流行程度的本地预警效应随着平均家庭规模的增大（英国2.371，印度尼西亚4.235，苏丹6.536）延迟敏感性降低，衰弱速度在小家庭规模种群中较快，在家庭规模较大的种群中衰减变慢，并在5－6个时步的延迟后其作用仍不可忽略。图2同时指出，在家庭规模很小的情况下（英国家庭），经历高延迟的本地预警效应已经大大降低，近乎可以忽略。一个合理的解释是，由于家庭规模较小，此时发生在初始传播家庭内部的传播过程已经接近结束，即所有的感染节点已经康复。显然，该现象与传播寿命与家庭规模的关系有关，因此，在图3中，利用潜伏期因素，对家庭传播过程的寿命与预警延迟性的相互关系进行了进一步讨论。

图1 延迟本地预警对早期动力行为的影响Fig.1 The impact of delayed local awareness on early dynamics

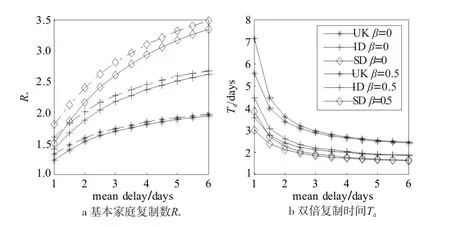
图2 不同家庭规模分布下延迟全局预警与本地预警的早期动力学影响Fig.2 The impact of delayed global and local awareness on early dynamics with different household size distributions

图3考察了不同潜伏期长时，不考虑接触频率条件下，即α＝0，基于流行程度的本地预警的延迟实施对早期动力学数值的影响。假设系统中不存在全局预警，即ρ＝0，τ＝0.1，β＝0.8。潜伏期变化分别用星号线、加号线、菱形线对应σ＝1、σ＝0.5和σ＝0.2（潜伏期长为1／σ）。图3a可以看出，只考虑流行程度的本地预警效应随着潜伏期长的变化出现临界点tdelay＝2，当平均延迟在［1，2］区域内时，潜伏期越短，本地预警越能够利用系统当前时刻的I（t）的数值实施其影响，R＊数值越小；随着实施延迟的增加tdelay∈（2，6］，本地预警对R＊影响变弱，此时潜伏期长对R＊的影响成为主要作用因素，潜伏期越短，第二子代家庭数R＊越大。对双倍复制时间Td，主要受到潜伏期长的影响，在tdelay∈［1，2］区域，本地预警对Td具有一定幅度的影响。

图3 潜伏期与延迟本地预警对早期传播行为的影响Fig.3 The impact of latent period and delayed local awareness on early spreading

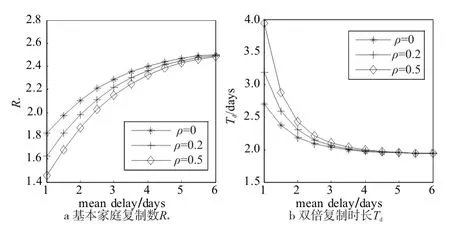
图4 延迟全局预警的早期动力行为影响Fig.4 The impact of delayed global awareness on early dynamics

在前面的数值仿真中，主要关注于本地预警与全局预警在其它动力学参数变化下，如家庭规模，家庭传播寿命等的变化下，其影响力的延迟敏感性。为了进一步比较两者的影响，同时也反映某些现实场景中存在的真实情况，此处考虑一种新的假设，即：系统中个体基于本地流行程度的防护举措始终存在，官方权威发布的全局预警却存在延迟。由此，设定α＝0.2，β＝0.5，本地预警从家庭拥有初始感染者开始，就立刻作用于家庭成员上，星号线、加号线、菱形线分别对应ρ＝0、ρ＝0.2和ρ＝0.5，全局预警则随延迟施加到系统中去。可以看出，在延迟与本地预警已作用两种因素下，不同强度的全局预警作用下的R＊和Td曲线在tdelay∈［5，6］区域趋向重合，意味着强度的增加已经不产生效果。一个合理的解释为：在这个时间段，I（t）在人口中的比例已经明显上升，本地预警对系统动力行为的影响大大增强，经过延迟施加在系统上的全局预警，已经对反映系统早期动力行为的指标R＊和Td拥有相对微弱的影响。

4 结语

文章探讨了预警信息接触次数，本地预警和全局预警的延迟实施对家庭网络的早期动力行为影响。通过对仿真数据比较发现，与一般直观猜想不同，基于流行的本地预警机制经由不同的延迟时间施加在系统中时，始终对系统早期动力行为拥有一定的不可忽略的作用，不论是低延迟实施在早期感染个体稀少的初始时刻，还是经历较高延迟后实施在感染者比例较高的系统状态下。仿真发现，考虑接触次数的本地预警，与一定取值下（ρ∈（0，0.5］）的全局预警相比较，具有更低的延迟敏感性。数据仿真中对参数取值的假设符合相关预警机制研究的一般假设：全局预警倾向造成传播率与脆弱性的减弱，而本地预警倾向于强防护甚至病毒传播的完全隔绝。由于家庭基本复制数等指标考察的是预警效应在家庭传播寿命里的累积作用，文章对潜伏期引起的家庭传播过程变慢，传播寿命变长的情况进行了分析。结果显示，相对于延长预警机制的作用时间，提高当前时刻的传播者个体数目对R＊的影响更大。因此，对比潜伏期与延迟预警的动力学影响力，出现临界点现象，低延迟短潜伏期系统，预警机制大大抑制了新感染个体出现；高延迟下，较短的潜伏期迅速转化已有感染者，其抑制效应强于预警作用。文章对预警机制的延迟分析，集中在本地预警与全局预警的延迟敏感性分析，以及引起敏感性指标变化的因素，如家庭规模分布，家庭传播寿命等。

［1］ 汪秉宏，周涛，王文旭，等.当前复杂系统研究的几个方向 ［J］.复杂系统与复杂性科学，2008，5（4）：21－28.Wang Binghong，Zhou Tao，Wang Wenxu，et al.Several directions in complex system research［J］.Complex Systems and Complexity Science，2008，5（4）：21－28.

［2］Funk S，Gilad E，Watkins C，et al.The spread of awareness and its impact on epidemic outbreaks［J］.Proceedings of the National Academy of Sciences of the United States of America，2009，106（16）：6872－6877.

［3］ Funk S，SalathéM，Jansen V A A，et al.Modelling the influence of human behavior on the spread of infectious diseases：a review［J］.Journal of The Royal Society Interface，2010，7（50）：1247－1256.

［4］ Gong Y W，Song Y R，Jiang G P.Epidemic spreading in scale－free networks including the effect of individual vigilance［J］.Chinese Physics B，2012，21（1）：41－45.

［5］ Wu Q C，Fu X C，Small M，et al.The impact of awareness on epidemic spreading in networks［J］.Chaos，2012，22（1）：0131011.

［6］ Bagnoli F，LiòP，Sguanci L.Risk perception in epidemic modeling［J］.Physical Review E，2007，76（6）：61904.

［7］ Funk S，Jansen V A A.Interacting epidemics on overlay networks［J］.Physical Review E，2010，81（3）：036118.

［8］ Black A J，House T，Keeling M J，et al.Epidemiological consequences of household－based antiviral prophylaxis for pandemic influenza［J］.Journal of The Royal Society Interface，2013，10：1019

［9］ Ross J V，House T，Keeling M J.Calculation of disease dynamics in a population of households［J］.PLoS ONE，2010，5（3）：e9666.

［10］Ball F G，Sirl D J，Trapman P.Analysis of a stochastic SIR epidemic on a random network incorporating household structure［J］.Mathematical Biosciences，2010，224（2）：53－73.

［11］Ross J V，Pagendam D E，Pollett P K.On parameter estimation in population models［J］.Theoretical Population Biology，2006，70（4）：498－510.

［12］Ghoshal G，Sander L M，Sokolov I M.SIS epidemics with household structure：the self－consistent field method［J］.Mathematical Biosciences，2004，190（1）：71－85.

［13］Pollett P K.Integrals for continuous－time Markov chains［J］.Mathematical Biosciences，2003，182（2）：213－225.