利用Sato模型研究上海及邻近地区尾波Q值

2015-12-19赵文舟

地震地磁观测与研究 2015年1期

陈婧赵文舟

1）中国合肥 230026 中国科学技术大学

2）中国上海 200062 上海市地震局

0 引言

介质的品质因子Q是地球介质的重要物理参数，表示了地球介质的非均匀性和非完全弹性，在地震研究的应用中具有很重要的作用。Aki（1969，1975）和Sato（1977）均提出了尾波散射理论，其中Aki利用单次散射波模型——由于S波在遇到散射体时所激发的单次散射波强并且单次散射模型适用于弱散射地区，认为由于地壳介质的非均匀性和地壳内部散射体的存在，能够较好地解释地震尾波在传播过程中的能量衰减。

前人对于尾波Q值的研究（张中天等，1990；马宏生等，2006；朱新运等，2006；季爱东等，2008；魏红梅等，2009 ）已经取得一些研究成果，很多研究者利用地方震尾波衰减研究尾波Q值的变化情况。有研究者认为，同一个地震的尾波Q值会随着流逝时间的增大而增大，而这能够反映以台站—震源为焦点的椭球体内范围内的平均介质状态，也反映了台站周围平均介质性质。有研究表明，在大震前存在尾波Q值的上升过程，并且在震后尾波Q值迅速降低，可以认为大震前存在应力积累使得裂隙闭合，反映出Q值升高；大震之后由于应力释放，使得地壳介质出现松散的情况，表现为Q值降低。

本次研究基于Sato模型，利用常熟地震台、金泽地震台、佘山地震台记录到的上海及邻近地区2011年至2013年区域数字地震波资料，采用Sato尾波单次散射模型，选定4个不同的流逝时间，计算尾波Q值，并对其特征进行讨论。

1 构造背景及资料选取

上海位于长江口南岸，地处扬子准地台东部边缘；西北沿郯庐断裂和胶南断裂与华北地台相接，东南以江山—绍兴深断裂为界与华南褶皱系相邻。上海地跨下扬子台褶带和浙西—皖南台褶带两个二级构造单元。扬子准地台是晚元古代末晋宁旋回形成的，基底具双层结构特征，地壳纵向分层、横向分块的特征较为明显，壳内低速层并不连续，上海所在的地块无明显低速层存在。上海北部的苏中沿海区域属于南黄海地震带，在构造上属于南黄海南部坳陷和勿南沙隆起区域。苏中沿海区域有东西走向并向东进入勿南沙隆起的拼茶河断裂，该断裂至今具有较强的孕震活动。本次研究采用数字地震波记录，仪器采样率100 Hz。选取2011年1月—2013年12月发生在上海及邻近地区、由3个台站分别记录的地震，震级ML2.0以上（取自上海台网数据目录），波形记录清晰，噪音水平满足记录条件。地震基本参数见图1和表1。

图1 上海及邻近地区震中分布Fig.1 Distribution of seismic epicenters inShanghai and adjacent area

表1 台站基本参数Table 1 Basic parameters of the stations

2 数据处理

2.1 分析方法

依照Sato模型（Sato H，1977），在特定频率下尾波振幅与时间的函数关系为

式中，AS是S波的最大振幅，Ac（t）是流逝时间t附近的尾波均方根振幅，t为从发震时刻起算的地震波流逝时间，tS为S波的流逝时间；C（ f ）是与频率相关的影响因子，对于震级相同的地震的同一频率，C（ f ）可视为常数；b为斜率，用于表征在不同频率点F （t）和 b（t－ tS）的线性关系；K （a）是与时间相关的传播因子，a ＝ t / tS。其中 K （a）、Ac（t）和b可用以下关系式表示AT为所取时间窗内地震波均方根，An为P波到达前一定时间记录的均方根，用来进行地震波的噪声校正（Pulli，1984；李白基等，2004）。由于 b 值可以有由 F （t）和 b （t－ tS）的线性关系求出，因此可以由式（4）求出Q值，之后对Q值进行拟合，则可得Q随频率的变化关系式中，Q0为f＝1 Hz时的品质因子，η为频率相关系数。需要说明的是，此程序分别计算各频率点的Q值，在同一频率下，对于同一地震而言：在被分析波形所持续的时间段内，仪器响应对波形的影响是一致的，不会影响Q值的大小。而式（1）也表明，这种随时间t的衰减与频率f有关，与地震大小、台站位置、震中距无关，则地震的场地响应得到抑制。

2.2 数据处理

本次研究利用基于Sato模型尾波Q值求解软件（朱新运等，2005）进行数据分析和计算，设定分析频率范围为4—18 Hz，间隔频率1 Hz，利用6阶Butterworth滤波器进行滤波，取S波时间窗长为2 s，步长为0.5 s进行计算，求取各频率点的平均振幅。为了对尾波Q值数据进行对比分析，分别采用80 s、100 s、120 s、140 s的流逝时间进行计算。图2为固定80 s流逝时间下的计算实例。

图2 流逝时间80 s地震计算实例

3 数据分析

本次研究利用挑选的数字地震波记录进行分析计算，并进行数据拟合，得到佘山地震台、金泽地震台、常熟地震台记录到的不同流逝时间下的Q0值（表2—表4）。

从表2—表4的结果可以看出，对于同一地震，Q值随着流逝时间的逐渐增加而增大，但是Q值的大小与震级大小并没有直接关系，与前人观点一致（Aki，1975；张天中等，1990）。通过对各个流逝时间段的数据分析，研究认为，在100 s和120 s流逝时间条件下，尾波Q值较为稳定；在80 s和140 s流逝时间下尾波Q值数据较为跳跃，并存在一定缺失现象，数据连续性较差。其原因可能为：随着流逝时间的增加，使得以台站—震中为焦点的椭球体的范围逐步扩大，且随着深度增加压力增大，但是地下介质的性质由于沉积等因素及不同构造背景的影响，对本次研究中流逝时间最短和最长的尾波Q值的连续性造成了一定程度的影响。

表2 佘山地震台记录的地震在不同流逝时间下的尾波Q0值计算结果Table 2 Calculated results of Q0 value under different elapsed time of Sheshan seismic record

表3 常熟地震台记录的地震在不同流逝时间下的尾波Q0值计算结果Table 3 Calculated results of Q0 value under different elapsed time of Changshu seismic record

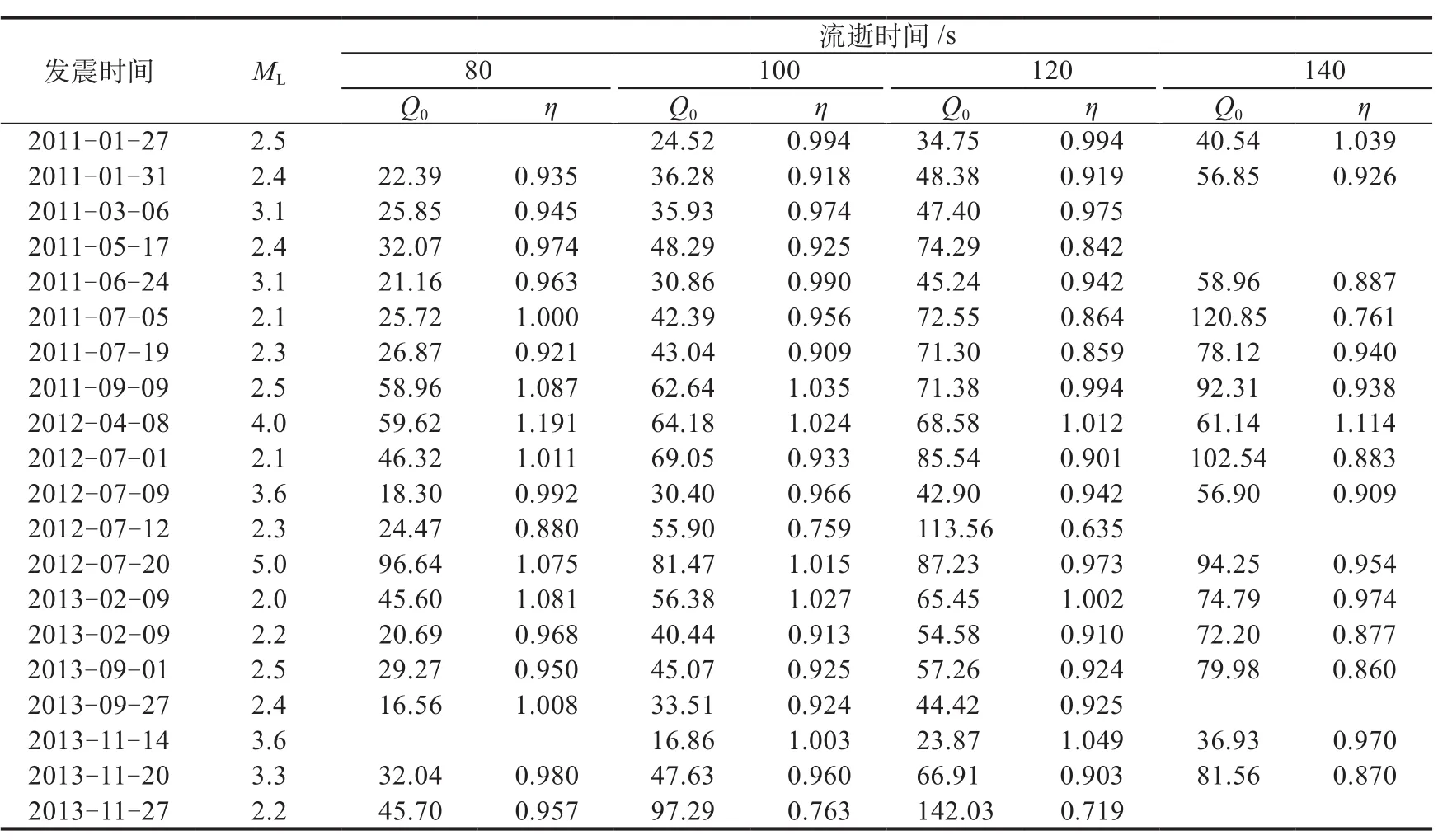
表4 金泽地震台记录的地震在不同的流逝时间下的尾波Q0值计算结果Table 4 Calculated results of Q0 value under different elapsed time of Jinze seismic record

本研究中，不同台站在同一流逝时间下得到的尾波Q值不同，但变化形态基本一致。以100 s流逝时间为例，对3个台站所得到的尾波Q0值进行分析：常熟地震台附近的尾波Q0均值为54.43，频率依赖性指数η为0.9602；金泽地震台附近的尾波Q0均值为42.08，频率依赖性指数η为0.9468；佘山地震台附近的尾波Q0均值为45.17，频率依赖性指数η为1.0023。这3个地区均表现出低Q0值、高频率依赖性。由图1发现上述3个台站周围地震活动性较弱，似乎与得出的结论不符。为此，我们对本研究区域ML1.0以上小震进行统计，发现3个台站周围小震活动较之前的统计结果有所增加，说明Q0值的结果还与小震活动有一定联系，小震活动越频繁，Q0值越低；小震活动越少，Q0值越高。

图3 3个台站记录的尾波Q0曲线

由图3可见，2012年7月20日江苏宝应ML5.0地震前， Q0值存在一个明显的上升过程，地震后又有一个明显的下降过程。可见，在2012年江苏宝应ML5.0地震前该区域的应力场存在一个增强过程，在尾波Q0值图像上表现为Q0值增大，在地震之后应力释放，尾波Q0值降低。图3中2013年11月27日上海崇明ML2.2地震为何Q值急剧增大，还需继续观察进行后续研究。

4 结论

尾波Q值反映了震源和台站周围介质的平均性质，是某个体积内介质的平均性质，通常认为Q值是岩石圈的一个构造参数，表示了地震运动在岩石圈所造成的破碎程度，是岩石圈裂隙密度的一个标志参数，在Q值、地壳运动和地震活动性之间存在着明显的相关性（刘希强等，2003；王卫东等，2004）。一般认为，地震活动性强的地区岩石破碎程度较高，Q值较小。从计算结果来看，本区域是低Q0值、强频率依赖性地区。

不同地震的尾波Q值对应不同的射线路径，不同的射线路径受到地下应力场、地质结构等的影响，在物理机制层面还与震源—台站为焦点构成的椭球面的范围相关。尾波Q值的大小反映了从震源至台站间椭球面范围内地震波的衰减情况。在计算过程中，流逝时间的不同影响着椭球体的大小。因此，为了方便对比不同流逝时间下的数据，固定流逝时间80 s、100 s、120 s、140 s。4种不同的流逝时间计算结果对比得出，相同地震的流逝时间选取越长，得到的尾波Q0值越大；地震目录基本相同的一组地震，在相同流逝时间下得到的尾波Q值的数值各不相同，但是按照地震顺序排列的形态基本一致。

本文在对2012年7月20日江苏宝应ML5.0地震的尾波Q0值序列进行分析时，发现在ML5.0地震前尾波Q0值在3个不同的台站上均表现出明显上升过程，并且在震后迅速下降并逐渐恢复到正常水平。此现象对于今后的Q0值分析具有一定意义。

尾波Q值计算软件由浙江省地震局朱新运研究员提供，计算所用波形数据由上海市地震局测震台网提供，在此深表谢意。

季爱东，李铂，张坤，等. 胶东地区地壳S波衰减系数和台站场地相应的研究[J]. 地震地磁观测与研究，2008，29（1）：44-49.

李白基. 云南姚安地区的尾波衰减[J]. 地震学报，2004，24（1）：47-52.

刘希强，沈萍，李红，等. 山东地区尾波衰减和小震震源参数变化特征研究[C].中国地球物理学会第19届年会，2003.

马宏生，刘杰，张国民，等. 云南地区尾波Qc值的分布特征及其初步解释[J]. 地震，2006，26（3）：37-43.

王卫东，张永志，狄秀玲，等. 1998年临猗5.0级地震Q值的时间变化特征[J]. 地震地磁观测与研究，2004，25（4）：56-60.

魏红梅，贺曼秋，黄世源，等. 重庆荣昌地区尾波Q值特征[J]. 西北地震学报，2009，31（1）：97-101.

张天中，高龙生，张卫平. 滇西试验场区的Q值及其随时间窗的变化[J]. 地震学报，1990，12（1）：12-21.

朱新运，杨钢宇，张震峰. 基于Sato模型的近震S波尾波Q值求解及分析软件研制[J]. 地震地磁观测与研究，2005，26（3）：64-70.

朱新运，张帆. 浙江及邻区尾波Q值研究[J]. 西北地震学报，2006，28（2）：108-113.

Aki K. Analysis of seismic coda of local earthquakes as scattered wave [J]. J Geophys， Res，1969，74 ：615-631.