考虑失效准则和沉降控制条件的基桩可靠度分析*
2015-12-19边晓亚郑俊杰徐志军章荣军
边晓亚,郑俊杰†,徐志军,章荣军
(1.华中科技大学 土木工程与力学学院,湖北 武汉 430074;2.河南工业大学土木建筑学院,河南 郑州 450052)
目前,桩基性能的优劣基本都是通过基桩承载力来评价的.由于土体变异性、地质勘察、现场试验、实验室测试、时间效应及荷载效应等不确定性因素的存在,基桩承载力具有很大的随机性.因为这些不确定性因素的存在具有客观性,影响着基桩的承载性能,所以产生了诸多确定基桩极限承载力的失效准则[1].
Zhang等[2]利用失效准则偏差系数,研究了失效准则在灌注桩承载力可靠度分析中的重要性.徐志军等[3]利用群桩效应系数和失效准则偏差系数,给出了不同失效准则下群桩可靠度分析方法.郑俊杰等[4]在基桩承载力目标可靠度的研究中指出,可靠度设计应首先确定采用的失效准则.
基桩可靠度分析,既要考虑承载力,又要关注位移,工程上要确保基桩承载力足够高、位移尽量小.这两个条件涉及到极限状态设计中的承载能力极限状态和正常使用极限状态问题.
针对基桩竖向位移即沉降问题,Wang等[5-6]推导出正常使用极限状态和承载能力极限状态下可靠度指标间的函数关系式,并研究了正常使用极限状态下建筑基础和打入桩的可靠性.Phoon等[7-8]采用两参数拟合曲线描述荷载-沉降关系,并用拟合参数来研究模型不确定性,为采用概率方法研究基桩正常使用极限状态下的可靠性提供了新的思路.
本文研究失效准则和沉降控制条件对基桩可靠度分析结果的影响,为此:通过定义承载能力极限状态和正常使用极限状态模型因子来衡量模型的不确定性;以s-lgt失效准则为基准,给出7种失效准则的偏差系数,以便提出考虑失效准则、模型不确定性和沉降控制条件等因素的基桩可靠度综合分析方法;分析容许沉降对可靠度分析结果的影响.
1 模型不确定性
1.1 承载能力极限状态
利用概率方法研究桩承载力的不确定性,需要搜集大量的试桩资料.但由于岩土工程中各种不确定性因素的存在,获得大量相同条件下基桩承载力的现场试验资料几乎是不可能的.为解决这一问题,诸多学者[9-10]采用承载力试计比(承载力的实测值与计算值之比)研究模型的不确定性.承载力试计比记为λuls,则

式中:Ruls和Rp分别为承载能力极限状态下基桩承载力的实测值和计算值.也可采用承载力试计比作为承载能力极限状态模型因子.
1.2 正常使用极限状态
在有关正常使用极限状态下基桩承载力特性的研究中,Phoon等[7-8]采用式(2)所示的两参数拟合双曲线来描述所研究桩型的荷载-沉降关系.

式中:Q为桩顶所受的竖向荷载;s为在荷载Q作用下的桩顶沉降量;a和b为荷载-沉降关系曲线的2个拟合参数.
由式(2)可知,荷载与沉降之间呈非线性单调递增关系,随着荷载的增加,桩顶沉降持续增加.当桩顶沉降达到某个容许极限值(slt)时,桩就处于正常使用极限状态,施加的荷载Q可作为基桩正常使用极限状态下的承载力[5],记为Rsls.此时荷载-沉降双曲线方程为:

定义参数λsls,使得:

易知,λsls是容许沉降slt的函数,可将其作为基桩的正常使用极限状态模型因子.且Rsls及模型的不确定性可通过模型因子λsls的统计特性来研究[7,10],该参数的均值μsls和变异系数COVsls计算式如下:

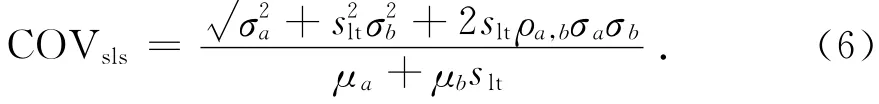
式(5)和式(6)中:μa和μb分别为参数a和b的均值;σa和σb分别为参数a和b的标准差;ρa,b为参数a和b的相关系数.
2 可靠度指标计算
如果仅考虑永久荷载和可变荷载,可利用均值一次二阶矩法求得可靠度指标β[11]:
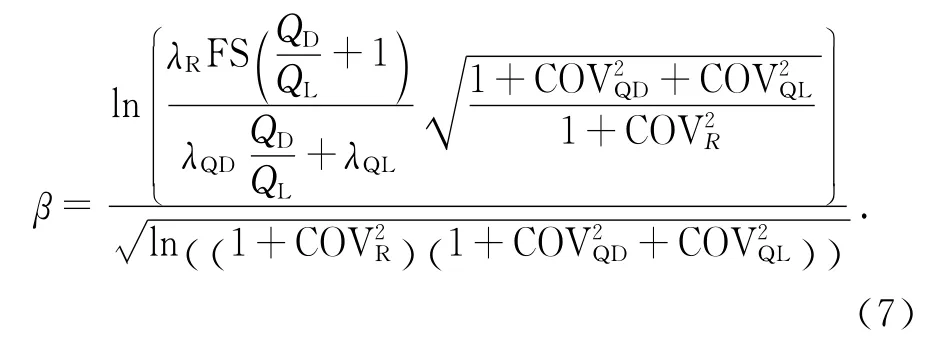
式中:λR,λQD和λQL分别为基桩极限承载力、永久荷载和可变荷载的偏差系数;COVR,COVQD和COVQL分别为基桩极限承载力、永久荷载和可变荷载的变异系数;FS 为容许应力设计法中的安全系数,本文取为3.0.λR和COVR取基桩承载力试计比的均值和变异系数.为研究失效准则对基桩承载力可靠度分析结果的影响,周建方等[1]和Zhang等[2]定义了不同失效准则的偏差系数λB:

式中:Rs-lgt和RB分别为由s-lgt法和其他失效准则确定的基桩极限承载力.
为比较分析,考虑以下7种国内外常用的确定钻孔灌注桩承载力的失效准则[1]:s-lgt法、沉降稳定时间法、波兰规范法、ISSMFE 准则、s-lgQ法、QS曲线法和FHWA 准则.由文献[1],给出有关失效准则相对于s-lgt法的偏差系数的概率统计分析结果(见表1).据此,可确定s-lgt法的偏差系数λB的统计量为:μB=1.00,COVB=0,表示无偏差.

表1 相对于s-lgt法的偏差系数Tab.1 Bias factors with respect to s-lgt failure criterion
当λuls的均值μuls和变异系数COVuls确定后,就可给出反映失效准则不确定性的基桩承载力综合试计比λUB的均值μUB和变异系数COVUB[2]:

式中:μB,COVB分别为失效准则偏差系数λB的均值和变异系数.
考虑沉降条件的要求,利用正常使用极限状态模型因子,得到考虑失效准则变异性、模型不确定性和沉降控制条件随机性等因素的基桩承载力综合试计比λUSB的均值μUSB和变异系数COVUSB[12]:

用式(9)和式(10)所示的基桩承载力综合试计比均值和变异系数来替代式(7)中的λR和COVR,便可得到考虑不同失效准则的基桩可靠度指标计算公式[2];用式(11)和式(12)所示的承载力综合试计比均值和变异系数来替代式(7)中的λR和COVR,便可得到考虑失效准则变异性、模型不确定性和沉降控制条件随机性等因素的基桩可靠度综合评价方法.
计算采用以下荷载参数统计值[1]:λQD=1.06,λQL=0.7,COVQD=0.07,COVQL=0.29.荷载比QD/QL分别取为0.5,1.0,2.0,3.0和4.0.
3 讨论与分析
3.1 参数分析
由文献[2],钻孔灌注桩承载力试计比的均值μuls和变异系数COVuls可分别取为1.00和0.13.
在正常使用极限状态可靠度分析中,模型因子λsls=Rsls/Ruls起着非常关键的作用.文献[5]采用Monte Carlo模拟和解析近似计算2 种方法,在容许沉降slt为96mm[13]时,对变量λsls进行比较分析,结果见表2.
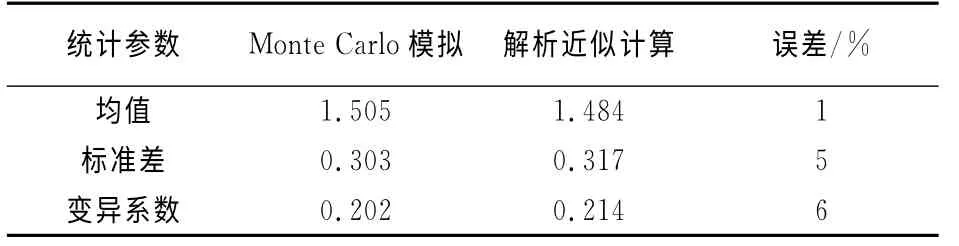
表2 变量λsls统计参数的比较Tab.2 Comparison of statistics of variableλsls
由表2知,采用Monte Carlo模拟和解析近似计算2种方法得到λsls的各项统计参数误差很小,不超过6%,两者高度的一致性表明,用λsls来估计正常使用极限状态模型不确定性具有较高的可信度.因此,在容许沉降slt为96mm 时,λsls的统计值可取为:μsls=1.50,COVsls=0.21.
3.2 可靠度分析
基于表1中各失效准则偏差系数的统计资料,由式(9)和式(10)及式(11)和式(12)可分别求出λUB和λUSB的均值和变异系数,见表3.
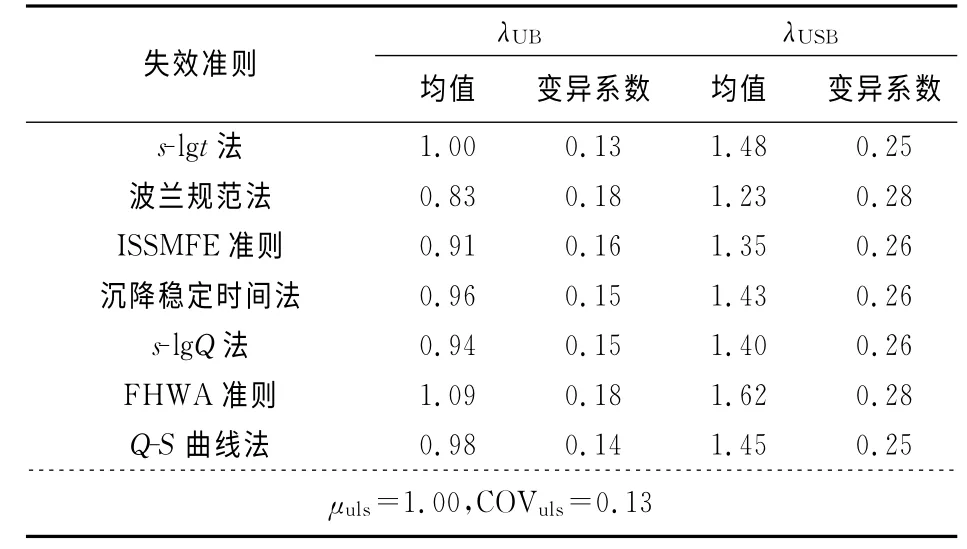
表3 λUB和λUSB的均值和变异系数(slt=96mm)Tab.3 Means and COVs ofλUBandλUSB(slt=96mm)
利用表3中λUB的统计参数,由式(7)计算得到未考虑基桩沉降变异性时不同失效准则对应的基桩可靠度指标,如图1所示.
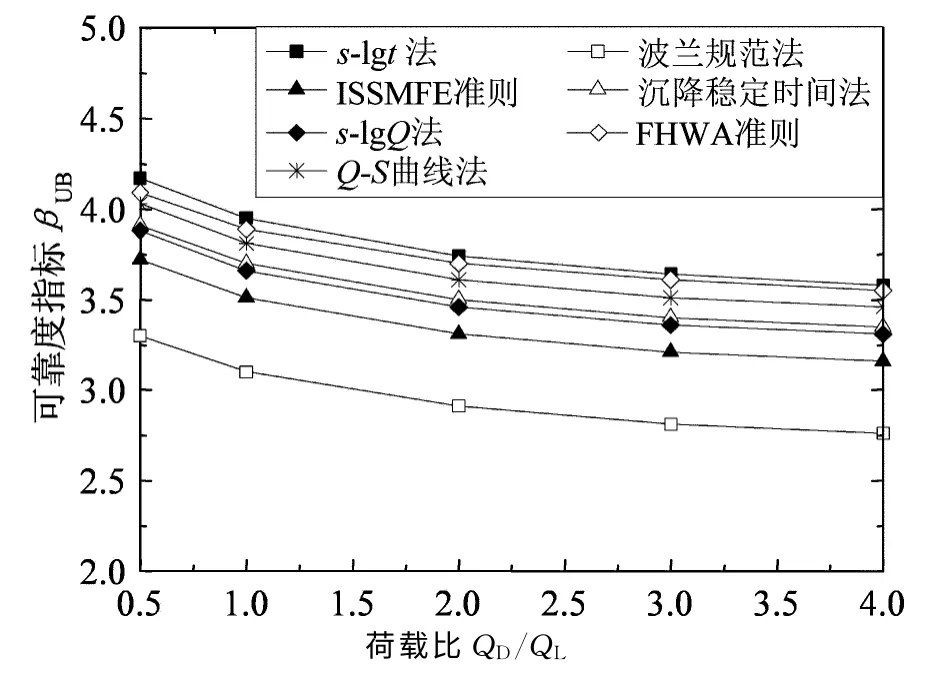
图1 不同失效准则的可靠度指标βUBFig.1 Reliability indicesβUBfor different failure criteria
由图1可知:根据不同失效准则计算的可靠度指标差别较大.其中,s-lgt法计算的可靠度指标最大,波兰规范法计算的可靠度指标最小,二者差值较大,达到0.84左右.这主要归因于s-lgt法的偏差系数均值较大,变异系数较小;波兰规范法的偏差系数均值较小,而变异系数较大.从而导致根据s-lgt法和波兰规范法计算的综合试计比均值和变异系数也产生较大差异,譬如,s-lgt法计算的综合试计比为1.00,变异系数为0.13;而波兰规范法计算的综合试计比仅为0.83,但变异系数达到0.18.
另外,虽然FHWA 准则对应的偏差系数均值为1.09,比s-lgt法的偏差系数均值大,计算的综合试计比均值也比s-lgt法计算的大,但FHWA 准则对应的变异系数也很大,所以根据FHWA 准则计算的可靠度指标就比s-lgt法计算的可靠度指标小.在几种失效准则的可靠度排序中,s-lgt法在第1位,FHWA 准则在第2位,波兰规范法排在最后.
因此,根据不同失效准则得到的可靠度水平的差异是失效准则偏差系数均值和变异系数共同作用的结果.
图2给出了同时考虑不同失效准则和沉降控制条件(slt=96mm)等因素时的可靠度计算结果.
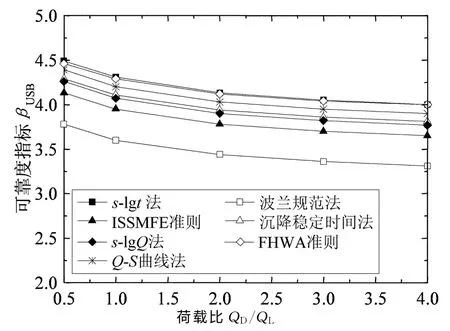
图2 不同失效准则的可靠度指标βUSB(slt=96mm)Fig.2 Reliability indicesβUSBfor different failure criteria(slt=96mm)
与图1相比,图2所示的不同失效准则可靠度指标曲线的排列顺序并没有发生改变,只是在正常使用极限状态模型不确定性和96mm 的沉降容许条件影响下,根据每种失效准则求得的可靠度指标都有显著的提高.譬如,由排在第1位的s-lgt法计算的可靠度指标几乎增加了0.4,由排在最后一位的波兰规范法计算的可靠度指标也是如此.但是,与图1相比,从图2中不同失效准则可靠度指标曲线相对位置的变化情况可以看出,根据每种失效准则求得的可靠度指标的提高幅度有差异.s-lgt法和FHWA 准则对应的可靠度指标曲线明显更加靠近,表明正常使用极限状态模型不确定性和96 mm 沉降容许条件使得s-lgt法和FHWA 准则的可靠度评价结果逐渐趋于一致.
3.3 考虑桩顶容许沉降slt的影响
作为比较,现考虑slt分别为15mm,25mm 和35mm 时的3种情况,对应的可靠度指标计算结果见图3.从中可以得到与图2所示的相似结果.

图3 不同失效准则的可靠度指标βUSBFig.3 Reliability indicesβUSBfor different failure criteria
综合图2和图3可知,随着slt的增大,求得的可靠度指标曲线逐渐升高,表明slt条件的放宽使得可靠度评价结果得到很大提高.但可靠度指标增长的幅度随slt的增大而逐渐降低,两者提高幅度不具有一致同步性.
另外,可靠度指标随slt的变化规律不受失效准则影响.为说明该结果,消除失效准则的影响,下面专门研究slt对可靠度分析结果的影响.为此,图4给出了不考虑沉降因素以及slt分别为15 mm,20 mm,25mm,30mm,35mm 和96mm 等7种情况下由各种失效准则求得的可靠度指标的平均值.
图4表明,随slt的增大,可靠度指标曲线逐步接近.譬如,slt为35mm 和96mm 时的2条曲线也比较接近.这表明当slt增大到一定水平后,沉降控制条件不再是影响基桩可靠度的主要因素.
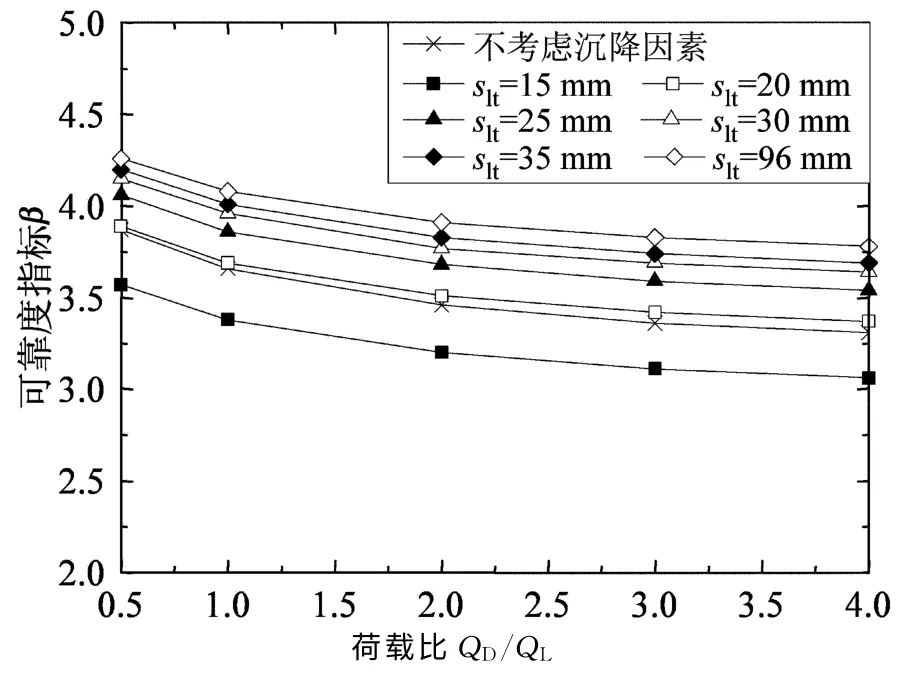
图4 不同沉降控制条件下的可靠度指标Fig.4 Reliability indices versus different settlement control levels
由图4还可看出,不考虑沉降因素时的可靠度指标曲线介于slt分别为15mm 和20mm 时的2条可靠度指标曲线之间,而且与slt为20mm 时的可靠度指标曲线极其接近.这表明承载能力极限状态与正常使用极限状态之间存在紧密联系,7种失效准则对基桩可靠度综合评价(以可靠度指标平均值来衡量)的结果,反映了slt为20mm 左右时的可靠度水平.
4 结 论
1)失效准则对基桩可靠度评价结果的显著影响,是失效准则偏差系数均值和变异系数共同作用的结果.
2)沉降控制条件对相应失效准则求得的可靠度指标值影响较大,但不改变由各失效准则求得的可靠度指标曲线排列顺序.
3)可靠度指标随slt的增大而增大,但增长的幅度逐渐降低,二者提高幅度的不一致同步性不受失效准则的影响.
4)承载能力极限状态与正常使用极限状态的基桩可靠度评价机理之间存在关联性.依所引用资料,7种失效准则对基桩可靠度综合评价结果,相当于slt为20mm 左右时的可靠度水平.
[1]周建方,李典庆.采用不同失效准则的桩基可靠度分析[J].岩土力学,2007,28(3):540-543.
ZHOU Jian-fang,LI Dian-qing.Reliability analysis of pile foundations considering different failure criteria[J].Rock and Soil Mechanics,2007,28(3):540-543.(In Chinese)
[2]ZHANG L M,LI D Q,TANG W H.Reliability of bored pile foundations considering bias in failure criteria[J].Canadian Geotechnical Journal,2005,42(4):1086-1093.
[3]徐志军,郑俊杰,边晓亚,等.基于不同失效准则的群桩可靠度分析[J].岩土工程学报,2012,34(5):819-825.
XU Zhi-jun,ZHENG Jun-jie,BIAN Xiao-ya,etal.Reliability analysis of pile groups based on different failure criteria[J].Chinese Journal of Geotechnical Engineering,2012,34(5):819-825.(In Chinese)
[4]郑俊杰,徐志军,边晓亚,等.考虑不同失效准则的基桩目标可靠度研究[J].华中科技大学学报:自然科学版,2012,40(5):76-79.
ZHENG Jun-jie,XU Zhi-jun,BIAN Xiao-ya,etal.Study on target reliability of piles under different failure criterion[J].Journal of Huazhong University of Science and Technology:Natural Science Edition,2012,40(5):76-79.(In Chinese)
[5]WANG Y,KULHAWY F H.Reliability index for service-ability limit state of building foundations[J].Journal of Geotechnical and Geoenvironmental Engineering,2008,134(11):1587-1594.
[6]WANG Y.Reliability index for serviceability limit state of drilled shafts under undrained compression[J].Journal of Geo-Engineering,2009,4(3):113-118.
[7]PHOON K K.Reliability-based design in geotechnical engineering:computation and applications[M].London:Taylor&Francis,2008:344-384.
[8]PHOON K K,CHEN J R,KULHAWY F H.Characterization of model uncertainties for augered cast-in-place(ACIP)piles under axial compression[C]//Proceedings of Sessions of GeoShanghai 2006.Shanghai,China,2006:82-89.
[9]ZHANG L M,TANG W H,NG C W W.Reliability of axially loaded driven pile groups[J].Journal of Geotechnical and Geoenvironmental Engineering,2001,127(12):1051-1060.
[10]DITHIDE M,PHOON K K,WET M D,etal.Characterization of model uncertainty in the static pile design formula[J].Journal of Geotechnical and Geoenvironmental Engineering,2011,137(1):70-85.
[11]WHITMAN R V.Evaluating calculated risk in geotechnical engineering[J].Journal of Geotechnical Engineering,1984,110(2):143-188.
[12]BIAN Xiao-ya,ZHENG Jun-jie,XU Zhi-jun.Incorporating serviceability limit state requirements into reliability-based analysis and design of piles[J].KSCE Journal of Civil Engineering,2015,19(4):904-910.
[13]ZHANG L M,NG A M Y.Probabilistic limiting tolerable displacement for serviceability limit state design of foundation[J].Geotechnique,2005,55(2):151-161.
