汽车制动作用下预应力混凝土简支梁桥的动力响应及冲击系数研究＊

邓 露，王 芳

（湖南大学 土木工程学院 风工程与桥梁工程湖南省重点实验室，湖南 长沙 410082）

目前，在车桥系统动力分析中将车辆假定为在桥上匀速运动的研究已经比较成熟［1－4］，而对于车辆荷载在桥上变速移动（刹车或者加速）下桥梁动力响应及冲击系数的研究较少，且模型比较简单，不能准确模拟汽车变速行驶下桥梁的真实响应．在已有的考虑汽车变速效应的车桥耦合振动的研究中，Law 和Zhu［5］，方志等［6］均是将桥梁简化为简支梁，将车辆荷载简化为集中荷载或简化的平面车辆模型；Gupta和Traill－Nash［7］将桥梁简化为梁单元和正交各向异性板两种模型进行车桥耦合振动的研究，结果显示将桥模拟为板单元得到的动力冲击系数比用梁单元得到的小，因此指出对复杂的车桥系统进行动力研究时有必要采用更精确的二维或三维桥梁模型．此外，殷新峰和方志［8］的研究发现汽车刹车产生的动力冲击系数可能会超过规范值．然而，在他们的研究中桥梁采用的是梁单元模型．

基于以上研究状况，本文建立了更加精确的三维有限元车桥模型研究汽车制动下的车桥耦合振动．选用一辆典型三轴重车模型获得了汽车制动时混凝土简支梁桥的跨中动力响应及冲击系数．对影响动力冲击系数的几个重要因素，如刹车位置、减速度、初速度、路面平整度及桥跨长度等进行了研究，并将计算的动力冲击系数与我国现行规范值进行了对比．

1 车辆、桥梁及路面平整度

1．1 车辆模型

本文选用了文献［2］中的典型三轴车辆模型．该车总质量32．63t．因重车为实际桥梁上的控制车辆荷载，故研究重车作用下的动力冲击系数．图1为车辆模型示意图，表1为其详细参数．

图1 三轴车模型Fig．1 Three－axle vehicle model

表1 车辆模型参数信息Tab．1 Major parameters of the vehicles under study

1．2 桥梁模型

本文所用的5座预应力混凝土简支梁桥跨度为9．14～39．62m．每座桥的宽度均为9．75m，桥面板厚度为0．2m．不同跨径的桥梁的高度和横截面均按规范设计．表2列出了5座桥的基本信息以及根据规范公式获得的动力冲击系数值．基于Ansys14．5平台，采用精度高的3D 实体单元solid45建立5座桥梁的有限元模型，具体建模过程和模型细节见文献［4］．图2为桥梁横截面及车辆加载位置，其中车辆沿车道2正中行驶．

图2 桥的横截面及车辆加载位置Fig．2 Bridge cross－section and vehicle loading position

表2 5座桥的基本参数Tab．2 Detailed properties of the five bridges

1．3 路面平整度

路面不平顺（通常用“路面平整度”来表征）是车－桥系统耦合振动的主要激励源，通常可用功率谱密度函数来描述路面的统计特性，如：

式中：n为空间频率，cycle／m；n0为参考空间频率，cycle／m；φ（n0）为路面平整度系数，m3／cycle；n1和n2分别为上下截止频率．

由上述功率谱密度函数通过逆傅立叶变换即可生成桥面平整度模型［9］．国际标准化组织将路面平整度分为A（非常好）到E（非常差）共5个等级［10］．本文采用其中好、中、差3种路面等级，图3为3种等级下的路面平整度样本．

图3 路面平整度样本Fig．3 Road roughness samples

2 变速行驶状态下车桥耦合系统运动方程及其求解

车辆匀速行驶情况下，通过车轮与桥面接触点处的位移和接触力之间的关系，可建立车桥耦合系统的动力学方程如下：

式中：M，C，K分别为质量、阻尼和刚度矩阵；d为系统位移向量；下标v和b分别代表车辆与桥梁；FG为 车 辆 重 力；Cb－b，Cb－v，Cv－b，Kb－b，Kb－v，Kv－b和Fb－r是由车－桥相互作用力引起的随时间变化的量．

运用模态叠加技术，方程（2）可简化为：

方程（3）只包含车的参数信息和桥的模态信息，因而大大简化了方程的求解．通过在Ansys中做模态计算，然后提取模态振型矩阵用于Matlab计算动力响应．微分方程求解使用四阶龙格库塔方法，具体的求解过程可参考文献［11］．

当行驶在桥上的车辆突然刹车时，车轮处的摩擦力与刹车引起的作用于车辆质心处的惯性力将形成一对仰俯力矩，即：

式中：FI＝－ma为作用于车辆质心处的惯性力，其中m为车辆质量，a为车辆水平加速度；hv为车辆质心距地面高度．该仰俯力矩使车辆产生仰俯运动，从而对桥梁产生冲击效应．将该仰俯力矩M作为外力加入文献［11］中用于计算匀速运动的三维车－桥模型程序中，即可模拟车辆变速运动的情况．值得注意的是，本文假设的是车辆匀变速过程，与以往的研究一致［5－6，8］．

3 汽车制动下桥梁跨中响应及接触力变化

选用桥3的跨中响应来说明汽车制动对桥梁响应的影响．汽车从桥梁左端入桥，初速度选用v＝20 m／s，加速度分别选用a＝－2 m／s2和－6 m／s2，路面平整度选用B级（即“好”），汽车前轮驶入桥梁入口3m 后（即1／8桥跨长）开始刹车．

3．1 桥梁跨中响应

图4（a）～（c）分别为车辆刹车作用下桥3的跨中挠度、应变和加速度响应图．其中匀速与静力响应的最大值也包含在图中，以对比刹车的效果．

由图4可以看出，汽车在桥上刹车时，桥梁跨中的挠度、应变及加速度均大于车辆匀速行驶情况，且随着减速度绝对值的增大而增大．

3．2 接触力变化

汽车刹车时，制动力产生的仰俯力矩会使汽车轴重发生重分布．对于单个车体，该仰俯力矩会导致前轮力增大，后轮力减小．对于本文所用的三轴车，从图5中可以看出，汽车在桥上静止时前轮接触力为17．5kN，中轴轮子和后轮的接触力为71kN，匀速运动时各轮接触力大小分别在静止时的接触力值上下浮动．汽车刹车时，前轮力增大，后轮力减小，且变化幅度随着加速度绝对值的增大而增大；对于中轴轮子，车体2和1上的仰俯力矩分别会使其接触力增大和减小，但由于车体2的质量大于车体1质量，所以在汽车刹车时该轮的接触力也是增大的，如图5所示．

图4 匀速与刹车下桥梁跨中响应Fig．4 Bridge responses at midspan with and without vehicle braking

图5 刹车时车的各轮轴接触力大小Fig．5 Contact forces for different axles under braking

4 动力冲击系数计算及参数分析

4．1 动力冲击系数计算

冲击系数通常被定义为：桥梁在行驶车辆作用下某特定位置上产生的最大动力响应的增大值与相应最大静力响应之比，即

式中：ydmax和ysmax分别为最大动响应和最大静响应，可由位移、应变和反力等响应计算得到，但由不同的响应得到的动力冲击系数值不一定完全相同［9］．中国现行规范JTG D60－2004《公路桥涵设计通用规范》按照桥梁基频计算动力冲击系数［12］．

本文计算了2种响应的动力冲击系数，即桥梁跨中处的挠度和应变动力冲击系数．针对每个工况的同一路面等级，随机生成20个路面平整度样本并计算动力冲击系数，最后求得平均值用于结果分析．

4．2 参数分析

本文分析的影响汽车制动下的动力冲击系数的参数有：1）7 个刹车位置：“L／8”～“7L／8”，即车前轮分别到达桥1／8～7／8跨度时开始刹车；2）3个减速度值：a＝－2m／s2，－4m／s2，－6m／s2；3）5个初速度值：v＝10 m／s，15 m／s，20 m／s，25 m／s，30 m／s；4）3个路面平整度等级：好，中，差；5）5种桥梁跨度：桥1（L＝9．14m）～桥5（L＝39．62m）．

4．2．1 刹车位置及减速度的影响

同样选用桥3的动力冲击系数结果来说明不同刹车位置及减速度对动力冲击系数的影响．图6给出了路面等级为“好”的情况下，3个不同减速度作用下在7个不同位置处刹车引起的动力冲击系数．匀速的结果也包含在图中以对比刹车产生的效果．为了避免单一的某个速度可能造成的偏差，此处的动力冲击系数均为相应刹车位置处5个速度下的平均值．

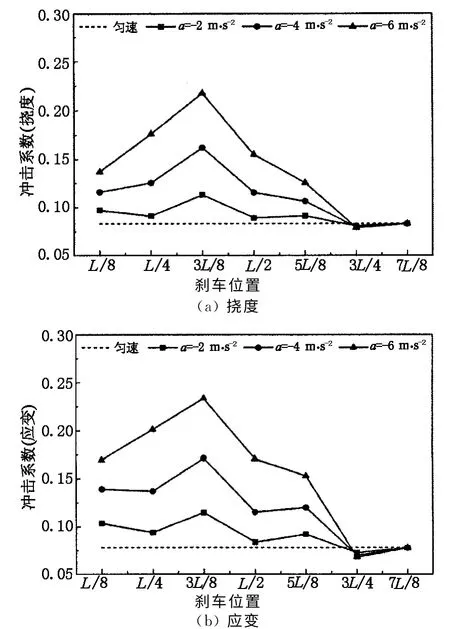
图6 不同减速度与刹车位置下的动力冲击系数Fig．6 Impact factors under different deceleration rates and braking positions

从图6可以看出：1）总体而言，车辆刹车对应的动力冲击系数明显大于匀速的结果，且动力冲击系数随着减速度绝对值的增大而增大；2）车辆在桥前半跨内刹车产生的动力冲击系数大于在后半跨度内刹车，这个结论与文献［5，7］相吻合；3）挠度冲击系数和应变冲击系数计算的结果趋势基本一致，但大小不完全相同．

4．2．2 初速度及平整度的影响

关于车辆行驶速度和路面平整度对动力冲击系数的影响在汽车匀速行驶的条件下已经进行了广泛的研究，结果表明动力冲击系数随速度的变化没有明显的规律；路面平整度对冲击系数的影响显著，冲击系数随着路面平整度的变差而增大［2－4］．

图7为3种路面平整度下桥3的动力冲击系数随初速度变化的情况．此时，加速度取为－6m／s2，刹车位置取最不利位置，即“3L／8”．图中实线与虚线分别为刹车与匀速情况的计算结果．

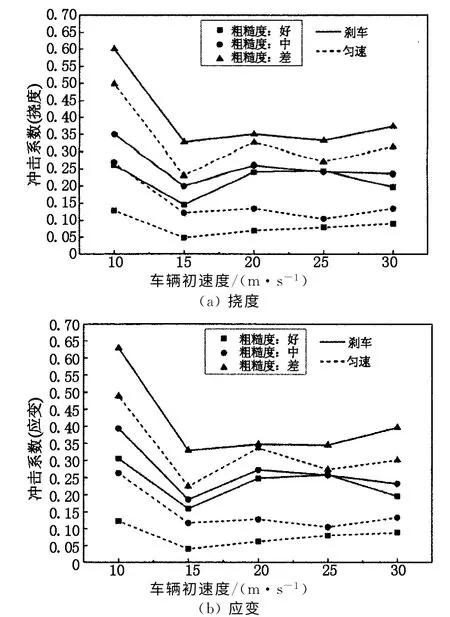
图7 不同初速度及平整度下的动力冲击系数Fig．7 Impact factors under different vehicle initial speeds and road surface conditions

从图7可以看出，与匀速结果类似：汽车制动时获得的动力冲击系数随速度的变化没有单调的递增或递减关系；随着路面平整度变差，动力冲击系数明显增大．另外值得注意的是：路面平整度越好，汽车制动时获得的冲击系数较之相应匀速行驶时的冲击系数增长的幅度越大，这一点在下一个参数分析时也有讨论．

4．2．3 桥跨长度的影响

表3列出了桥1～5在汽车速度v＝20m／s时刹车与匀速行驶时的动力冲击系数结果，并将计算的IM 值与用我国规范给出的公式计算的值进行了对比．其中刹车下的冲击系数取自加速度a＝－6 m／s2时7个刹车位置处产生的最大值．用相对差值（DIFF）表示刹车时的冲击系数相对于同种条件下车辆匀速产生的冲击系数的增量，即：

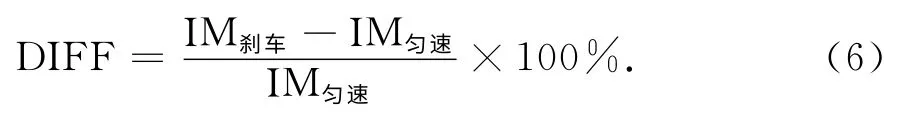
式中：IM刹车与IM匀速分别为相同条件下汽车刹车与匀速行驶时的动力冲击系数．

从表3可以看出：1）当其他条件相同时，IM刹车明显大于IM匀速，相对差值最大可超过300%；2）对于桥2～桥5，相对差值基本是随着桥跨长度的增大而减小，说明刹车对短跨桥的影响更大；3）路面平整度越好，IM 对刹车反应越敏感．以桥3为例：当平整度等级为“好”时，刹车时的挠度冲击系数相对于匀速行驶时的相对差值为244．32%，而当平整度等级为“差”时，相应的相对差值降为10．65%．

另外，从表3还可以看出，当路面平整度为“好”时，IM刹车与IM匀速均小于规范值，说明我国规范对于此种路况下的桥梁的设计与评估是满足要求的．而当路面平整度为“中”或“差”时，满足规范要求的IM匀速对应工况下的IM刹车可能超过规范值．例如桥2路面平整度为“差”时，IM匀速小于规范值，而相应的IM刹车则超过规范值，桥3路面平整度为“中”时的情况亦如此，表明在桥梁评估时必须考虑到汽车刹车作用对冲击系数的影响．

表3 汽车制动下5座桥的动力冲击系数对比Tab．3 Comparison of impact factors of the five bridges due to vehicle braking

5 结 论

本文利用三维车桥模型研究了汽车制动下的车桥耦合振动．获得了典型三轴重车在混凝土简支梁桥上刹车时桥梁的跨中动力响应及冲击系数，讨论了刹车位置、减速度、速度、路面平整度及桥跨长度对冲击系数的影响规律．得出以下主要结论：

1）汽车制动时桥梁的动力响应及冲击系数均明显大于车辆匀速行驶情况，且增长幅度随着减速度绝对值的增大而增大．

2）车辆在桥前半跨内刹车的动力冲击系数值大于在后半跨内刹车的值．

3）速度对动力冲击系数的影响较复杂．动力冲击系数并不随车速的增大而单调递增或递减，这与车辆匀速的情况类似．

4）路面平整度对动力冲击系数的影响显著，匀速与刹车情况下动力冲击系数均随着路面平整度的变差而增大；当路面平整度等级为差时，匀速行驶时的动力冲击系数的绝大部分值及汽车刹车时的全部冲击系数值均超过规范值，故维护桥面状况对于减少车辆的动力冲击效应具有很重要的意义．

值得注意的是，本研究发现，在若干工况下，车辆匀速行驶时的冲击系数满足规范要求，而相应的刹车作用下的冲击系数则超出了规范值．因此，在桥梁评估时必须考虑到汽车刹车作用对冲击系数的影响．本文的研究结果可以为工程实践中评估混凝土简支梁桥时动力冲击系数的采用提供一定的参考依据．

［1］王解军，张伟．汽车荷载作用下梁桥的动力冲击效应研究［J］．振动与冲击，2007，26（6）：125－128．

WANG Jie－jun，ZHANG Wei．Study of dynamic impact effects of moving vehicle loading on beam bridge［J］．Journal of Vibration and Shock，2007，26（6）：125－128．（In Chinese）

［2］邓露，何维，王芳．不同截面类型简支梁桥的动力冲击系数研究［J］．振动与冲击，2015，34（14）：70－75．

DENG Lu，HE Wei，WANG Fang．Dynamic impact factors for simply supported bridges with different cross sections types［J］．Journal of Vibration and Shock，2015，34（14）：70－75．（In Chinese）

［3］BRADY S P，O’BRIEN E J A．Effect of vehicle velocity on the dynamic amplification of a vehicle crossing a simply supported bridge［J］．Journal of Bridge Engineering，2006，11（2）：241－249．

［4］DENG L，CAI C S．Development of dynamic impact factor for performance evaluation of existing multi－girder concrete bridges［J］．Engineering Structures，2010，32（1）：21－31．

［5］LAW S S，ZHU X Q．Bridge dynamic responses due to road surface roughness and braking of vehicle［J］．Journal of Sound and Vibration，2005，282（12）：805－830．

［6］方志，殷新锋，彭献．非匀速车辆与随机路面桥梁的耦合振动分析［J］．振动与冲击，2008，27（1）：30－36．

FANG Zhi，YIN Xin－feng，PENG Xian．The coupled vibration analysis of with uneven surface and speed－varying vehicle［J］．Journal of Vibration and Shock，2008，27（1）：30－36．（In Chinese）

［7］GUPTA R K，TRAILL－NASH R W．Bridge dynamic loading due to road surface irregularities and braking of vehicle［J］．Earthquake Engineering ＆Structural Dynamics，1980，8（2）：83－96．

［8］殷新峰，方志．车辆制动作用下的车辆－路面－桥梁系统随机振动分析［J］．计算力学学报，2010，27（5）：936－941．

YIN Xin－feng，FANG Zhi．Random vibration analysis of vehicle－pavement－bridge system under vehicle braking［J］．Chinese Journal of Computational Mechanics，2010，27（5）：936－941．（In Chinese）

［9］漆景星．公路桥梁冲击系数计算方法研究［J］．公路，2011（7）：85－89．

QI Jing－xing．A study on calculation method of impacting force withstood by highway bridges［J］．Highway，2011（7）：85－89．（In Chinese）

［10］ISO 8068：1995 Mechanical vibration－Road surface profiles－reporting of measured data［S］．Geneva：ISO，1995．

［11］DENG L，CAI C S．Identification of parameters of vehicles moving on bridges［J］．Engineering Structures，2009，31（10）：2474－2485．

［12］JTG D60－2004 公路桥涵设计通用规范［S］．北京：人民交通出版社，2004．

JTG D60－2004 General code for design of highway bridges and culverts［S］．Beijing：China Communications Press，2004．（In Chinese）