地下水位动态序列分析与预报研究

2015-12-19朱世芳

西部探矿工程 2015年6期

关键词：趋势水位动态

邹晔，胡莹，朱世芳

（山东省鲁南地质工程勘察院，山东兖州272100）

地下水位动态序列分析与预报研究

邹晔*，胡莹，朱世芳

（山东省鲁南地质工程勘察院，山东兖州272100）

根据地下水水位动态资料的特点，将地下水位非平稳时间序列分解为趋势项函数、周期项函数和随机项3部分，并叠加后建立组合数学模型，对地下水水位动态进行预测。最后通过实例检验，此种建模和预报理论取得了较好的效果。

地下水水位动态；非平稳时间序列；预测

1 概述

地下水动态取决于地下水的补给、径流与排泄条件，是受地形地貌、地层岩性、气象和水文等自然因素和人工开采、灌溉、排水等人为因素综合作用的结果。地下水动态反映了地下水要素随时间变化的状况，为了合理利用地下水或有效防范其危害，必须掌握地下水动态。

目前国内外已经有很多学者研究了采用随机性数学模型进行地下水水位动态的预测，其中受到大家公认的方法主要包括回归分析法、频谱分析法和时间序列分析法等。在各种随机模型中，无论是频谱分析法还是时间序列分析法，都要求地下水动态序列满足平稳性条件，而实际中的地下水动态序列，由于人为干扰因素越来越大以及观测时间的有限性，绝大部分序列都不满足平稳性条件，而是存在一个趋势项。此外，由于各种随机因素的作用，单一的周期加趋势项模型必然会产生大量残差，即随机项，从而使预报的精度大大降低。为此本文尝试运用参数模型方法研究非平稳性地下水动态序列。

2 非平稳时间序列分析

2.1 非平稳时间序列模型

所谓非平稳时间系列，即表示统计性质随时间而异的存在非常广泛的那一类物理数据，在实际问题中经常遇到的时间序列一般都是非平稳的。由于非平稳时间序列的一般性和复杂性特点，对它至今尚无统一处理的一般方法。

设D（t）是时间t的确定性函数，R（t）是一个各态历经的平稳随机过程，通常可以采用加法模型来研究非平稳过程，作为实际物理过程的近似，

由H（t）的测量数据，用一种统计的方法估计函数D（t）所含的一些参数，识别、提取、预报趋势函数项D（t）。人们把这样一类方法，称为参数模型方法。

在时间序列分析中，识别、提取趋势项D（t），是很重要的一项工作。为了提取D（t），一般假定D（t）由2部分组成，即：

式中：T（t）——实际测量数据随时间t变化的主值函数项；

P（t）——由实测数据中可分离出来的周期函数项。

因此，一个非平稳时间序列可以认为是由趋势成分、近似周期成分和平稳随机成分组成，而平稳时间序列则要求统计参数的期望值与方差不随时间改变。

2.2 非平稳时间序列建模

2.2.1 建模思路

非平稳水位动态序列H（t）是由趋势成分T（t）、近似周期成分P（t）和平稳随机成分R（t）组成，其可表示为3个组成部分之和，表达式为[1]：

H（t）=T（t）+P（t）+R（t）

在非平稳水位动态模型中，趋势项T（t）反映变量的多年变化趋势；周期项T（t）反映变量的周期性变化。趋势项、周期项这2项反映了时间序列变量变化中的确定性成分，把这2项分离出去，余下的就是随机项了。随机项可用平稳时间序列来分析，其可分为2项：平稳时间序列项S（t）和纯随机项N（t），即：

R（t）=R（t）+N（t）

其中纯随机项N（t）作为白噪声来处理。

将时间序列变量分解成3个组成部分之后，就可按各组成项的变化规律对未来时刻进行外推，再将各项合成作出预报。

2.2.2 地下水水位动态时间序列模型的建立

（1）趋势项分析：趋势项是指在时间序列中，序列稳定而规则的变动，即随时间的推移对平均值来说增大或减小的趋势，其可能是线性的，也可能是非线性的。趋势项数学模型的结构基本上由人们的经验判定，当无法判定趋势项应采用何种形式的数学结构时，通常用确定性模型拟和趋势成分T（t），用逐步回归方法对模型系数加以求解。

对于趋势分量T（t）可用多项式逼近，即：

由此，可采用多元回归方法确定待定系数c0，c1，c2，…，c10和阶数。其具体求解方法通过编程序统一处理来实现。如果经逐步回归计算，回归系数全为零，可以认为（3）式无趋势项T（t）。

（2）周期项分析：

①频谱分析方法：周期分量是序列随着时间的推移而呈现出的周期性成分。时间序列分离趋势之后，将剩余的序列P（t）=H（t）-T（t）进行周期分析。识别和提取周期项P（t）的方法有方差分析、频谱分析和周期图分析等，这里主要采用频谱分析法。

频谱分析是利用傅立叶级数把某个资料的时间序列表示成无数个不同周期的简谐波和的形式来分析序列变化规律的一种方法。对序列P（t）可用L个波叠加的形式表示其周期项[2]：

其中的每个项为一个分波，分别称Ai，ωi，φi为第i个分波的振幅、频率和相位，a0为一常数。因为

sin( ) ωit+φi=sinωitcosφi+cosωitsinφi

并令：

ai=Aisinφibi=Aicosφi

则P（t）可以改记为：

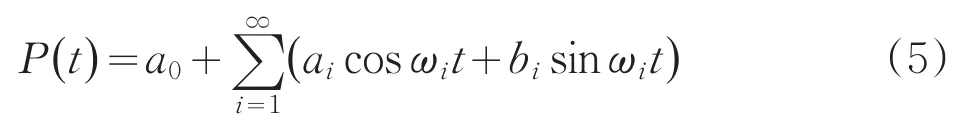
由于观测资料的有限性，无法进行无穷分波，因此一般假定P（t）有K个分波（试验周期个数），即：

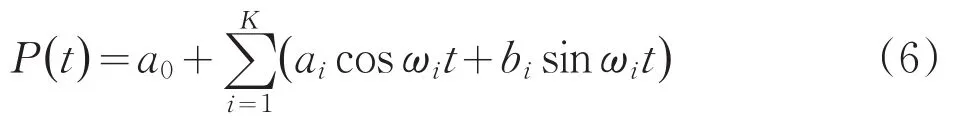
对于给定的时间序列可用以下的方法来确定a0，ai，bi，i=1，2，…，K。设有n个水位H（t），t=1，2，…，n，n为样本的长度，除去其趋势项T（t）后，余下的序列记为P（t），即P（t）=H（t）-T（t），t=1，2，…，n，又认为K个分波各有年的周期，即第i个分波，周期为：

因而第i个分波的频率为：

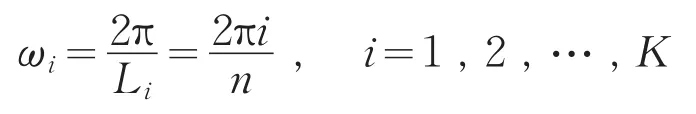
于是：

可以采用最小二乘法来确定系数a0，ai，bi，通过一系列推导，可以求得：

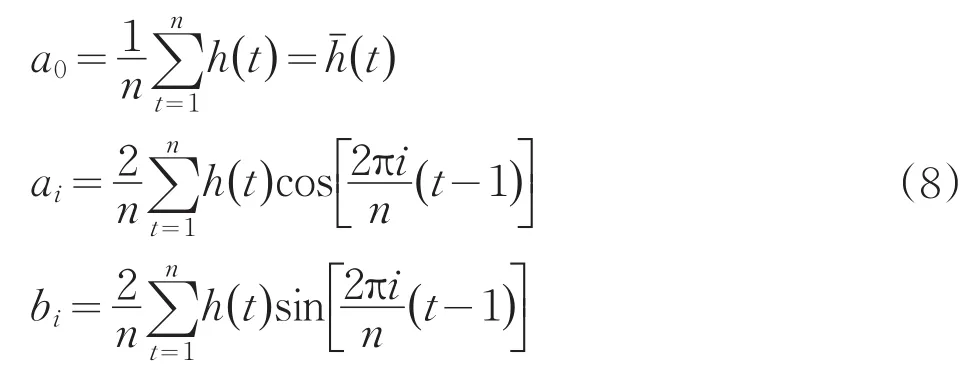
如何从上述求得的各分波系数ai，bi中选取主要周期。常用下面2种方法推求。

②主要周期判断：本次分析用振幅的大小判断主要周期。

因：

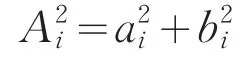
故：

在显著水平为0.05时，若：

则认为相应的第i个分波是主要周期，上式中的n为样本长度，K为试验周期个数，σ2为序列P（t）的方差，可用样本方差S2来估计。通过推导能够证明S2可用下式来计算：

其中：

若A1，…，Ak中有M个分波满足（9）式，则我们在（6）式中只保留相应的M个项即可，即最后求得P（t）的周期项为：

在实际应用中为节省工作量，通常在L个波中选取波动比较显著的几个谐波相加得到周期项，一般只需选取前6个显著谐波就能满足精度要求了。

（3）随机项分析：随机分量是指各时刻的序列值与前一个时刻或几个时刻值存在着某种相关关系的成分。时间序列模型中，消除趋势项和近似周期项后的剩余序列，即为平稳随机系列项，此时，即可用平稳随机模型方法来分析求解。

①求解数学模型：在数理统计中，我们已知回归模型为：

它表示观测值yt对另一组观测值（x1t，x2t，…，xkt）的相依性，上式可以视为由2部分组成，一部分取决于自变量（x1t，x2t，…，xkt），而另一部分则是随机成分εt。观测序列｛yt｝是假定为相互独立或不相关的。

对时间序列xt=x（t）（假定属平稳序列，且均值为零）有[3]：

上式为p阶自回归模型，常记为AR（p），式中φ1，φ2，…，φp为待定常数，称它们为自回归系数，εt表示在量测过程中存在的随机干扰和未来预报中出现的误差。我们假定t时的观测误差εt与t以前的观测值xt-j，j=1，2，…，p独立，因而有：

②自回归系数的确定：自回归系数φ1，φ2，…，φp的确定有2条途径。

其一是用xt-i乘（14）式两边，得到：

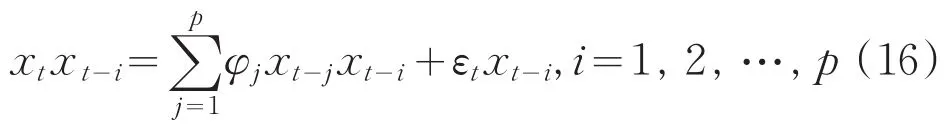
上式两边取数学期望，并利用（15）式得：

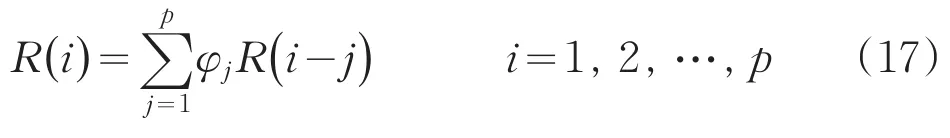
此即一组p阶线性方程：

式中：R（1），R（2），…，R（p）可以用估计值r（1），r（2），…，r（p）来代替，于是从理论上讲由（18）式便可以解出φ1，φ2，…，φp。

根据x1，x2，…，xN为各态历经平稳时间序列的假定，可以用下式估计相关函数r（τ）[4]：

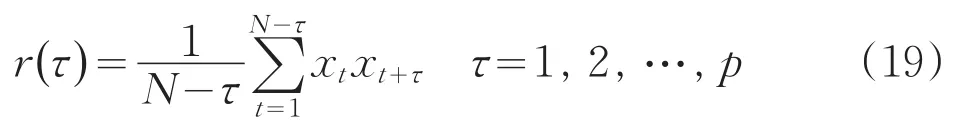
若x1，x2，…，xp未标准化，需先标准化如下：

然后对xb1，xb2，…，xbN使用（19）式。这样，我们得到自回归系数φ1，φ2，…，φp的相应估计值b1，b2，…，bp，它们满足p阶方程组：

式中r（p）[r（τ）]即为相关函数R（p）[R（τ）]的估计值，见式（21）。

另一途径用最小二乘估计的方法来决定（14）式中的系数φ1，φ2，…，φp，即选φ1，φ2，…，φp，使：

为最小值[5]。上式关于φj，j=1，2，…，p分别求偏导数，得：

由各态历经性的假定有：

于是（22）式两边除以N-p，据（23）式，便得：

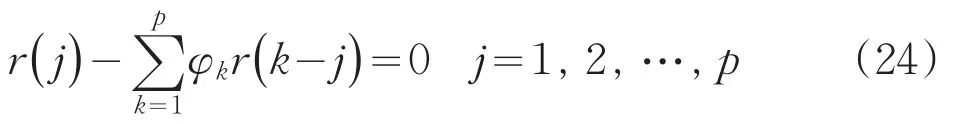
将φk改记为bk再展开后，它与（20）式完全一样。

用各种代数方法求解方程组，得φ1，φ2，…，φp。

③自回归模型阶数p的确定：上面给出了自回归模型（14）式，从上面的过程可以看出，如果取的阶数p不同，则所得的模型也不同，因此便提出一个问题：究竟p应是多少，才可使得求出的自回归模型（14）最佳？这实际上是个模型识别问题。

在使用上可以这样考虑：给出一个误差范围，例如0.01，即（14）中的 ||εt＜0.01，然后对不同的p进行计算，直至满足 ||εt＜0.01的那个p为止，最后所得结果便是所要的值。

3 实例验证

为了验证文中所提理论，笔者收集了某钻孔1996～2012年的1224个水位值（每个月6个水位观测值）作为建模数据，利用文章所提理论确定了模型，趋势分析模型参数C0取3.510，C1取0.0042，其它模型参数结果见表1和表2。模型对1994～2012年水位进行了拟合，取得了较好的效果，实际水位与拟合水位对比图见图1，同时利用建立的模型对该钻孔2013～2027年的水位进行了预报（见图1）。