High-Order Fully Coupled Scheme Based on Compact Integrated RBF Approximation for Viscous Flows in Regular and Irregular Domains
2015-12-19TienThaiQuangMaiDuyTranandTranCong
C.M.T.Tien,N.Thai-Quang,N.Mai-Duy,C.-D.Tranand T.Tran-Cong
High-Order Fully Coupled Scheme Based on Compact Integrated RBF Approximation for Viscous Flows in Regular and Irregular Domains
C.M.T.Tien1,N.Thai-Quang1,N.Mai-Duy1,C.-D.Tran1and T.Tran-Cong1
In this study,we present a numerical discretisation scheme,based on a direct fully coupled approach and compact integrated radial basis function(CIRBF)approximations,to simulate viscous f l ows in regular/irregular domains.The governing equations are taken in the primitive form where the velocity and pressure f i elds are solved in a direct fully coupled approach.Compact local approximations,based on integrated radial basis functions,over 3-node stencils are introduced into the direct fully coupled approach to represent the f i eld variables.The present scheme is verif i ed through the solutions of several problems including Poisson equations,Taylor-Green vortices and lid driven cavity f l ows,def i ned on domains of different shapes.The numerical results obtained by the present scheme are highly accurate and in good agreement with those reported in earlier studies of the same problems.
Compact integrated RBF,fully coupled approach,regular/irregular domains,viscous f l ow,Poisson equations,Taylor-Green vortices,lid driven cavity.
1 Introduction
In the primitive variable discrete formulation of the incompressible Navier-Stokes equations,the treatment of the velocity-pressure coupling has a major inf l uence on the convergence rate of the f l uid f l ow simulation.In the incompressible Navier-Stokes equations,the pressure appears only through its gradient in the momentum equations and is only indirectly specif i ed via the continuity equation.The lack of a dedicated equation for the pressure causes diff i culty in solving the incompressible Navier-Stokes equations.Numerous approaches of coupling between the velocity and pressure f i elds have been studied to overcome this problem in the past decades.
There are generally two approaches for the issue of the velocity-pressure storage and coupling:segregated approaches and fully coupled approaches.
The segregated approach,in which the continuity and momentum equations are solved sequentially,leads the most often to a so-called pressure correction method.The fi rst attempt of the segregated method was introduced by Patankar and Spalding(1972),in which the pressure fi eld is determined by two processes: fi rst computing an intermediate fi eld based on a guessed pressure fi eld;then conducting a correction process to ensure the new velocity satis fi es the continuity equation.A dif fi culty of this approach lies in the lack of a pressure time derivative term in the continuity equation.Several methods have been proposed to overcome this drawback and they are classi fi ed by the way in which the incompressibility constraint is imposed.Among them,the commonly used methods are the so called pressure based schemes in which the velocity-pressure coupling is solved iteratively.The velocity variables are updated in the momentum equations and the pressure fi elds are computed in pressure equations.The updating procedure is processed by the well-known SIMPLE(Semi-Implicit Method for Pressure Linked Equations)or SIMPLEC(SIMPLE-Consistent)or SIMPLER(SIMPLE-Revisited)or PISO(Pressure-Implicit with Splitting of Operator)algorithm[Acharya,Baliga,Karki,Murthy,Prakash,and Vanka(2007)].The algorithms improve the robustness of the pressure solver controlling its convergence rate and bring signi fi cant bene fi ts for the overall method.However,the main shortcoming of these methods,where the velocity-pressure coupling is not enforced at each stage of iteration through the solution of the linearised system,is that the convergence slows down when the number of grid points increases[Deng,Piquet,Queutey,and Visonneau(1994a);Pascau and Perez(1996);Elman,Howle,Shadid,and Tuminario(2003);Ammara and Masson(2004);Darwish,Sraj,and Moukalled(2009)].
The fully coupled approach,in which the discretised equations of all variables are solved as one system,has been investigated as an alternative to the segregated approach.In these approaches,no explicit equation for pressure or for pressure correction is required and the momentum and continuity equations are discretised in a straightforward manner.Caretto,Curr,and Spalding(1972)proposed the coupled solution for the momentum equations and the continuity equation,the so-called SIVA(SImultaneous Variable Adjustments)algorithm.In this approach,the coupling between dependent variables is structured in small sub-domains.The resulting matrices in such approaches are easy to compute but poor convergence rates are obtained,due to the weak coupling between sub-domains,especially on f i ne grids.Multigrid methods[Vanka(1986a);Bruneau and Jouron(1990)]have been developed to overcome this problem;however,they do not appear to bring signif i cant improvement in comparison with standard pressure based methods[Deng,Piquet,
Queutey,and Visonneau(1994a)].Some other examples of the fully coupled algorithm include the SCGS(Symmetrical Coupled Gauss-Seidel)of Vanka(1986a),the UVP method of Karki and Mongia(1990),among others.The absence of a pressure equation in these fully coupled algorithms may lead to an ill-conditioned system of equations because zeros are present in the main diagonal of the discretised continuity equation[Darwish,Sraj,and Moukalled(2009)].Attempts have been made to deal with this issue,with various degrees of success,through the use of preconditioning[May and Moresi(2008);Henniger,Obrist,and Kleiser(2010)],penalty methods[Braaten and Patankar(1990);Pascau and Perez(1996)],orbyalgebraicmanipulations[ZedanandSchneider(1985);Galpin,Doormaal,and Raithby(1985)].These treatments may improve the stiffness of equations.Mazhar(2001)presents a fully coupled approach differing from the aforementioned approaches in the sense that a direct attempt is made to solve the primitive difference equations.
In[Hanby,Silvester,and Chew(1996)],a fully coupled procedure is presented and compared with the SIMPLEC solver.The comparison shows that a fully coupled solution gives quicker convergence with less nonlinear(or outer)iteration.Braaten and Shyy(1986)investigated the effects of mesh skewness,Reynold number and grid size on the iterative and direct solution methods.The results show the fully coupled fully implicit treatment of equations in the direct sparse matrix method leads to rates of convergence that are much more rapid than the iterative method.The work also indicates the importance of retaining the coupling between velocity and pressure f i elds in obtaining the superior rate of convergence of the direct scheme.Whilst a fully coupled method requires more computer memory than a segregated approach,this is not a serious limitation on most current computers and it may offer advantages in terms of robustness,CPU time,and level of convergence.
Radial basis function networks(RBFNs)have emerged as a powerful numerical method for the approximation of scattered data[Fasshauer(2007)].Kansa(1990a)andKansa(1990b)f i rstproposedtheconceptofusingdirect/differentialRBF(DRBF)approximation for solving partial differential equations(PDEs).In the DRBF method,the closed form RBF approximating function is f i rst obtained from a set of training points and the derivative functions are then calculated directly from such closed form RBF[Mai-Duy and Tran-Cong(2001a)].Mai-Duy and Tran-Cong(2001b)and Mai-Duy and Tran-Cong(2003)then proposed the idea of using indirect/integrated RBF(IRBF)for the solution of PDEs.In the IRBF approach,the highest derivatives under interest are decomposed in to RBFs;the expressions for the lower derivatives and its functions are then obtained through integration processes.Numerical studies in[Mai-Duy and Tran-Cong(2001a);Mai-Duy and Tran-Cong(2001b);Mai-Duy and Tran-Cong(2003);Mai-Duy and Tran-Cong(2005)]have shown that the integral approach is more accurate than the differential approach because the integration process is averagely less sensitive to noise.To employ a larger number of collocation points,a one-dimensional IRBF scheme has been developed in literatures[Mai-Duy and Tanner(2007);Mai-Duy and Tran-Cong(2007)].Recently,Mai-Duy and Tran-Cong(2013)have proposed a 3-point compactIRBF(CIRBF)stencilwhereonlynodalvaluesofthesecond-orderderivative(i.e.extra information)are incorporated into the approximations.Thai-Quang,Mai-Duy,Tran,and Tran-Cong(2012)has proposed another 3-point CIRBF stencil where the extra information includes nodal values of both the f i rst-and secondorder derivatives.The latter scheme with tri-diagonal matrices was reported to be more accurate and eff i cient[Thai-Quang,Mai-Duy,Tran,and Tran-Cong(2012)].This article implements a direct fully coupled approach for the f l uid f l ow simulation with the f i eld variables being approximated on uniform/non-uniform Cartesian grids by the CIRBF approximation scheme presented in[Thai-Quang,Mai-Duy,Tran,and Tran-Cong(2012)].The tight velocity-pressure coupling is developed on a collocated grid and one global system of equations involving the velocity and pressure is solved simultaneously in its primitive form.In this way,momentum and continuity conservation equations are satisf i ed implicitly and simultaneously over the whole grid points.The use of fully coupled fully implicit solver for Navier-Stokes equations exhibits rapid convergence and provides the stability for large time steps to be employed[Elman,Howle,Shadid,and Tuminario(2003)].A block preconditioning technique[Henniger,Obrist,and Kleiser(2010)]is used to ref i ne the direct solution only when the coeff i cient matrix is ill-conditioned(e.g.the problem of irregular bottom lid driven cavity).
The remainder of this paper is organised as follows:Section 2 outlines the governingequationsandafullycoupledapproach.Followingthis,ablockpreconditioning technique is brief l y described in section 3.Section 4 describes the spatial disretisation using CIRBF stencils.In Section 5,numerical examples are presented and the CIRBF results are compared with some benchmark solutions,where appropriate.Finally,concluding remarks are given in Section 6.
2 Mathematical model
The transient Navier-Stokes equations for an incompressible viscous f l uid in the primitive variables are expressed in the dimensionless non-conservative forms as follows.
Conservation of x-momentum

conservation of mass(continuity)

where u,v and p are the velocity components in the x-,y-direction and static pressure,respectively;Re=Ul/ν is the Reynolds number,in which ν,l and U are the kinematic viscosity,characteristic length and characteristic speed of the f l ow,respectively.For simplicity,we employ notations N(u)and N(v)to represent the convective terms in x-and y-directions,respectively;and,L(u)and L(v)to denote the diffusive terms in x-and y-directions,respectively.
The temporal discretisations of(1)-(3),using the Adams-Bashforth scheme for the convective terms and Crank-Nicolson scheme for the diffusive terms,result in

wherendenotesthecurrenttimelevel;GxandGyaregradientsinx-andy-directions,respectively;and Dxand Dyare gradients in x-and y-directions,respectively.
Taking the unknown quantities in(4)-(6)to the left hand side and the known quantities to the right hand side,and then collocating them at the interior nodal points result in the matrix-vector form

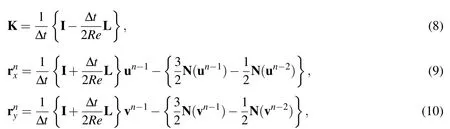
3 Preconditioning technique
For simplicity,we def i ne

Block-oriented preconditioning methods for the Navier-Stokes equation decompose the block 2×2 matrix in(12)using a block-LU decomposition

By def i ning Schur complement as S=DbK−1G[Silvester,Elman,Kay,and Wathen(2001)],the block upper triangular preconditioner is expressed as

Substituting(13)into(12),we can obtain the Schur complement for the pressure[May and Moresi(2008);Henniger,Obrist,and Kleiser(2010);Furuichi,May,and Tackley(2011)].It yields the following block upper triangular system

The velocity and pressure solutions are obtained via block back substitution in(15),i.e.solving the following systems

In this work,it is noted that the preconditioning technique is required whenever the coeff i cient matrix is ill-conditioned.In particular,it is only used to stiffen the coeff i cient matrix for the problem of an irregular bottom lid driven cavity in Section 5.6.
4 Spatial discretisation
For the approximation of the f i rst-and second-order derivatives in(7),a compact IRBF(CIRBF)scheme of Thai-Quang,Mai-Duy,Tran,and Tran-Cong(2012)is employed in this paper.It is represented as follows.
Consider a two-dimensional domain Ω,which is represented by a uniform Cartesiangrid.Thenodesareindexedinthex-directionbythesubscriptand in y-direction by jFor rectangular domains,let N be the total number of nodes(i.e.N=nx×ny)and Nipbe the number of interior nodes(i.e.Nip=(nx−2)×(ny−2)).For non-rectangular domains,selection of interior nodes is detailed in Section 5.2.At an interior gridwhere i∈{2,3,...,nx−1}and j∈{2,3,...,ny−1},the associated stencils to be considered here are two local stencils:in the x-direction andin the y-direction.Hereafter,for brevity,η denotes either x or y in a generic local stencilillustrated in Figure 1.

Figure 1:Compact 3-point 1D-IRBF stencil for interior nodes.

The integral approach starts with the decomposition of the second-order derivative of a variable,u,into RBFs where m is taken to be 3 for local stencils;is the set of RBFs;andthe set of weights/coef fi cients to be found.Approximate representations for the fi rst-order derivative and the function itself are then obtained through the integration processes

4.1 First-order derivative compact approximations
Extra information used in the compact approximation of the fi rst-order derivative is chosenWe construct the conversion system over a 3-point stencil associated with an interior node in the form


which maps the vector of nodal values of the function and its f i rst-order derivative to the vector of RBF coeff i cients including the two integration constants.Approximate expressions for the f i rst-order derivative in the physical space are obtained by substituting(24)into(19)

where η1≤ η ≤ η3and u=[u1,u2,u3]T.(25)can be rewritten as
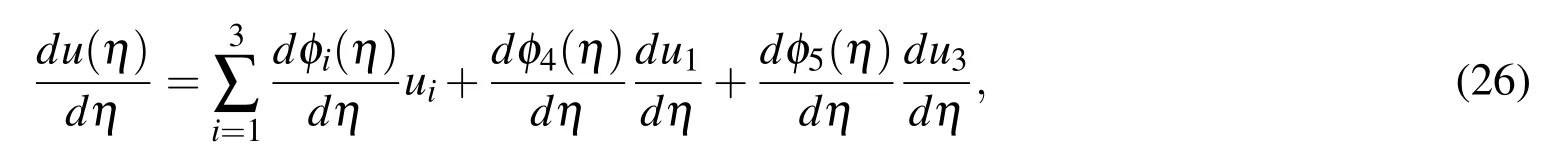

where nodal values of the f i rst-order derivative on the right hand side are treated as unknowns.Collocating(27)at η = η2results in

or in the matrix-vector form


Figure 2:Special compact 4-point 1D-IRBF stencil for boundary nodes.
At the boundary nodes,the f i rst-order derivatives are approximated in special compact stencils.Consider the boundary node,e.g.η1.Its associated stencil is{η1,η2,η3,η4}as shown in Figure 2.The conversion system over this special stencil is presented as the following matrix-vector multiplication


The boundary value of the f i rst-order derivative of u is thus obtained by substituting(33)into(19)and taking η = η1

where u=[u1,u2,u3,u4]T.(34)can be rewritten as
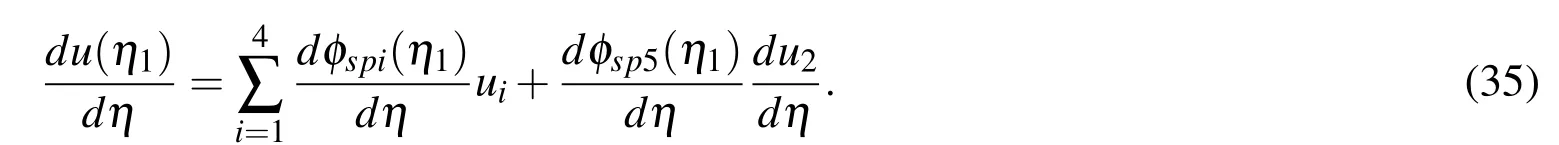
At the current time level n,(35)is taken as

or in the matrix-vector form

In a similar manner,one is able to calculate the f i rst-order derivative of u at the boundary node ηnη.The IRBF system on a grid line for the f i rst-order derivative of u is obtained by letting the interior node taking values from 2 to(nη−1)in(29)and making use of(38)for the boundary nodes 1 and nη,resulting in

where Qηand Rηare nη×nηmatrices.
4.2 Second-order derivative compact approximations
Extra information used in the compact approximation of the second-order derivative are chosen asWe construct the conversion system over a 3-point stencil associatedan interior node in the form


Solving(40)yields

which maps the vector of nodal values of the function and its second-order derivative to the vector of RBF coeff i cients including the two integration constants.Approximate expressions for the second-order derivative in the physical space are obtained by substituting(42)into(18)

where η1≤ η ≤ η3and u=(43)can be rewritten as
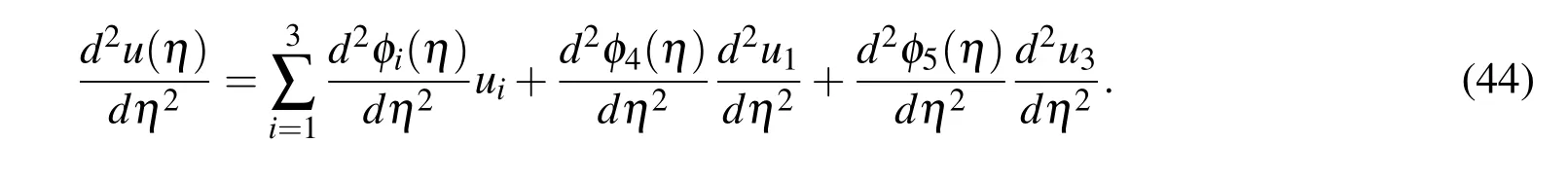
At the current time level n
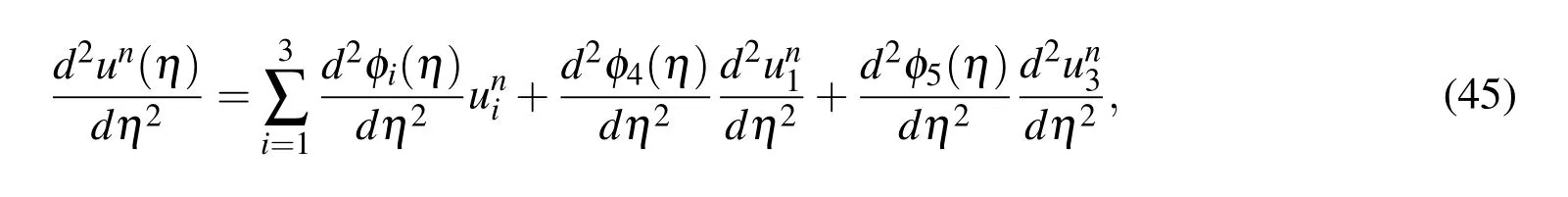
where nodal values of the second-order derivative on the right hand side are treated as unknowns.Collocating(45)at η = η2leads to

or in the matrix-vector form

At the boundary nodes,the second-order derivatives are approximated in special compact stencils.Consider the boundary node,e.g.η1.Its associated stencil isas shown in Figure 2.The conversion system over this special stencil is presented as the following matrix-vector multiplication
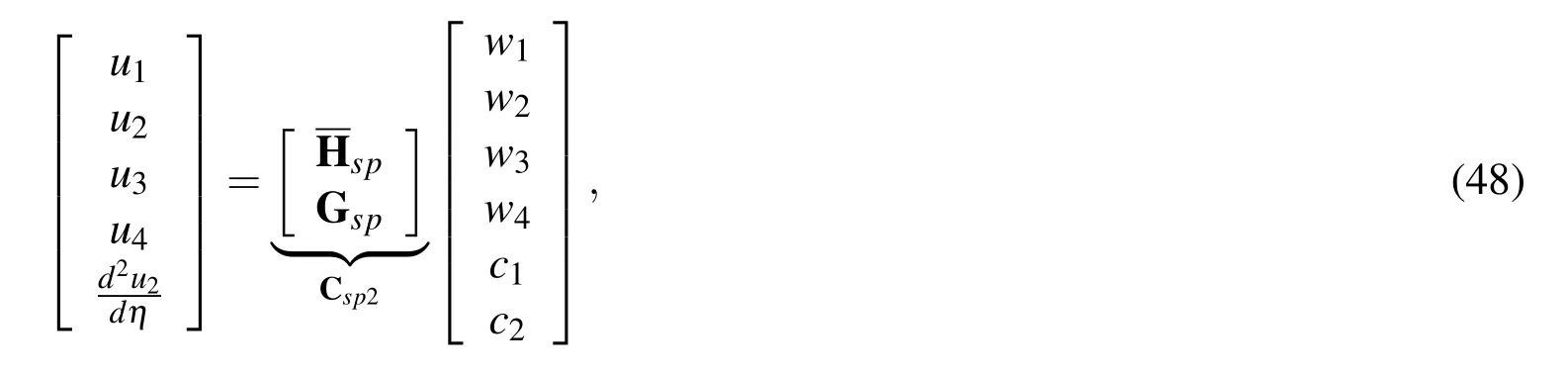
where Csp2is the conversion matrix;Hspis de fi ned as before(i.e.(31))and Gspis de fi ned as
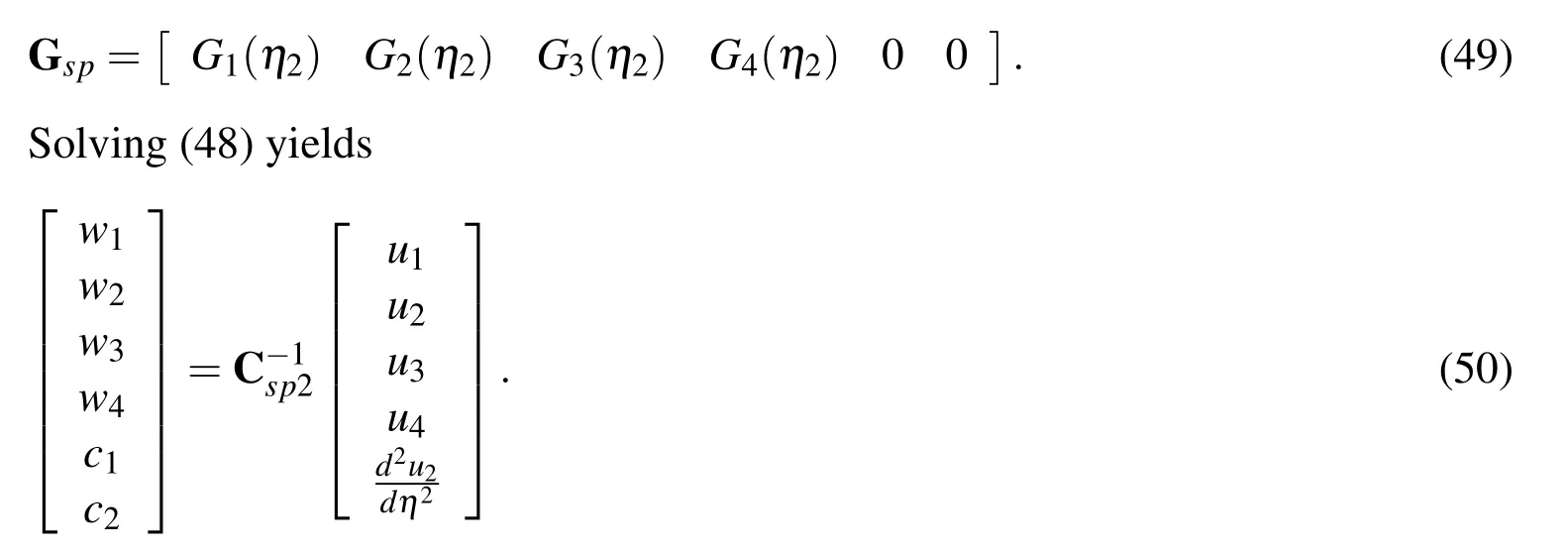
The boundary value of the second-order derivative of u is thus obtained by substituting(50)into(18)and taking η = η1
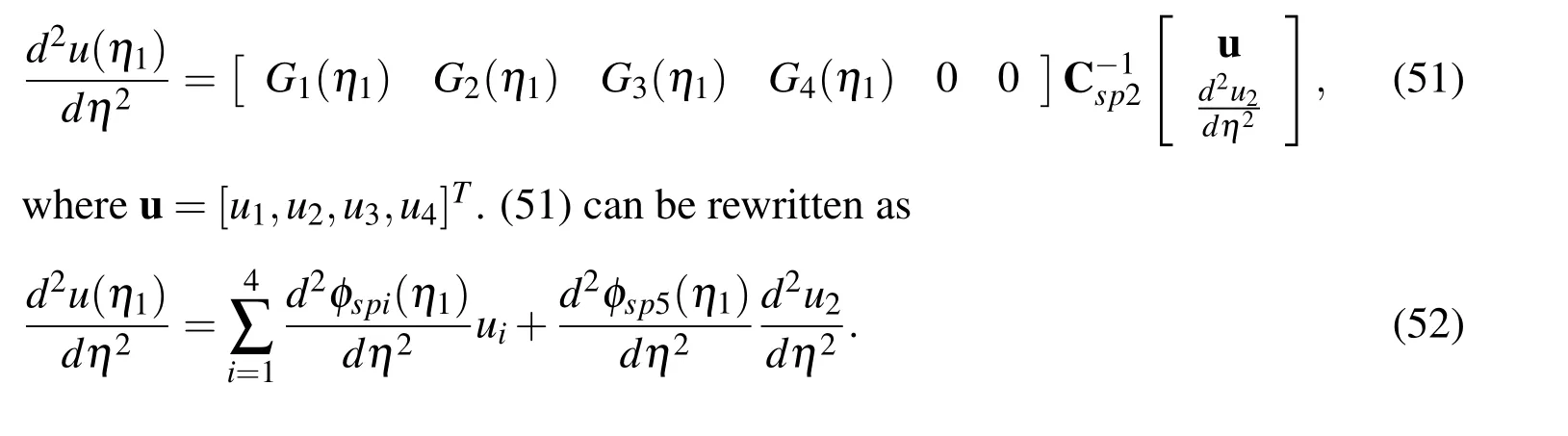
At the current time level n,(52)is taken as

In a similar manner,one is able to calculate the second-order derivative of u at the boundary node ηnη.The IRBF system on a grid line for the second-order derivative of u is obtained by letting the interior node taking values from 2 to(nη−1)in(47)and making use of(55)for the boundary nodes 1 and nη,resulting in

5 Numerical examples
We chose the multiquadric(MQ)function as the basis function in the present calculations

where ciand aiare the centre and the width of the i-th MQ,respectively.For each stencil,the set of nodal points is taken to be the same as the set of MQ centres.
We simply choose the MQ width as ai= βhi,where β is a positive scalar and hiis the distance between the i-th node and its closest neighbour.The value of β=40 is chosen for calculation in Section 5.4 and β=50 for the rest of calculations in the present work.We evaluate the performance of the present scheme through the following measures
i.the root mean square error(RMS)is def i ned as

where fiandfiare the computed and exact values of the solution f at the i-th node,respectively;and,N is the number of nodes over the whole domain.ii.the maximum absolute error(L∞)is de fi ned as

iii.the global convergence rate with respect to the grid ref i nement is def i ned
through

where h is the grid size;and,γ and α are exponential model’s parameters.iv.a f l ow is considered as reaching its steady state when

5.1 Poisson equation in rectangular domain
In order to study the spatial accuracy of the present CIRBF approximation scheme in a rectangular domain,we consider the following Poisson equation[Mai-Duy and Tran-Cong(2010)]
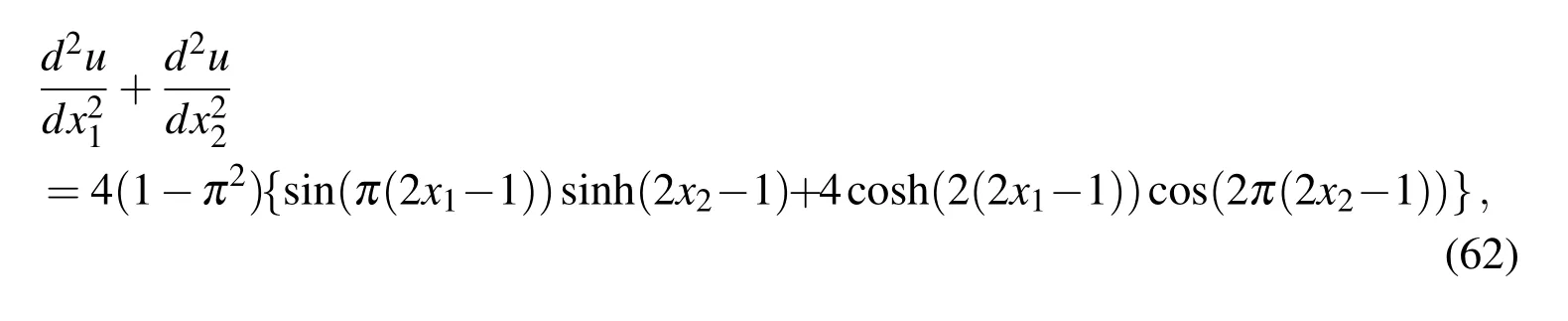
subject to Dirichlet boundary condition derived from the following exact solution

on a square domain[0,1]2.The calculations are carried out on a set of uniform grids of{41×41,51×51,...,91×91}.Figure 3 shows that present scheme outperforms the fourth-order compact FDM(Finite Difference Method)by Tian,Liang,and Yu(2011)and second-order standard FDM in terms of both accuracy and rates of convergence.The solutions converge as O(h5.23)for the present scheme,O(h4.56)for the compact FDM,and O(h1.99)for the standard FDM.Figure 4 shows that the matrix condition number grows with approximately the same rate of O(h−2.00)for the three methods.
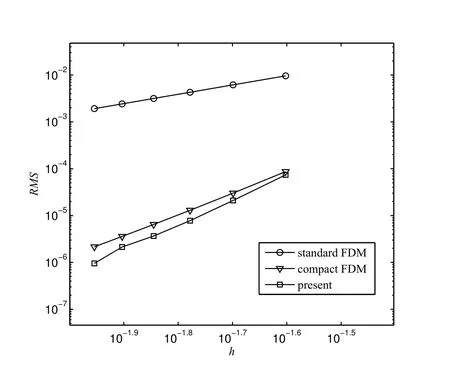
Figure 3:Poisson equation,rectangular domain,{41×41,51×51,...,91×91}:The effect of grid size h on the solution accuracy RMS.
5.2 Poisson equation in non-rectangular domain
To study the spatial accuracy of the present CIRBF approximation scheme in a non-rectangular domain,we consider the following Poisson equation[Mai-Duy and Tran-Cong(2010)]

Figure 4:Poisson equation,rectangular domain,{41×41,51×51,...,91×91}:The effect of grid size h on the matrix condition number.

on a circular domain with radius of 1/2.The problem domain is embedded in a uniform Cartesian grid and the grid nodes exterior to the domain are removed.The interiornodesfallingwithinasmalldistanceδ=h/8,wherehisthegridsize,tothe boundary will also be discarded[Mai-Duy and Tran-Cong(2010)].The boundary nodes are generated through the intersection of the grid lines and the boundary as demonstrated in Figure 5.Calculations are carried out on a set of uniform grids,{20×20,30×30,...,90×90}.Figure 6 shows that the present compact IRBF has better performance than second-and fourth-order compact FDM schemes proposed by Gamet,Ducros,Nicoud,and Poinsot(1999).The present scheme yields a fast rate of convergence of O()while the compact FDM produces a rate of O()for the fourth-order scheme and Ofor the second-order scheme.Figure 7 shows that the matrix condition number increases with approximately the same rate of O()for the three methods.
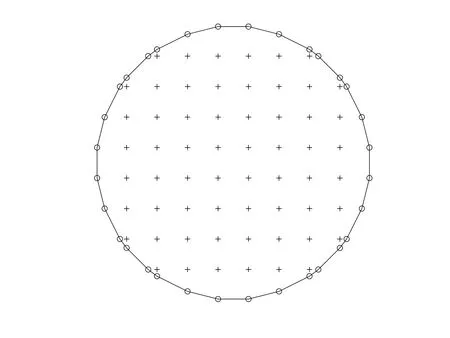
Figure 5:Poisson equation,non-rectangular domain,spatial discretisation:+,interior nodes;◦,boundary nodes.
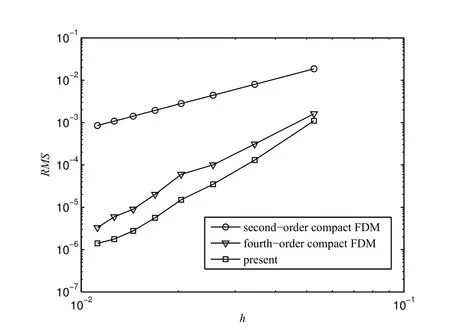
Figure 6:Poisson equation,non-rectangular domain,{20×20,30×30,...,90×90}:The effect of grid size h on the solution accuracy RMS.

Figure 7:Poisson equation,non-rectangular domain,{20×20,30×30,...,90×90}:The effect of grid size h on the matrix condition number.
5.3 Taylor-Green vortex in rectangular domain
To study the performance of the fully coupled approach,based on CIRBF approximation,in simulating viscous fl ow in a rectangular domain,we consider a transient fl ow problem,namely Taylor-Green vortex[Tian,Liang,and Yu(2011)].This problem is governed by the Navier-Stokes equations(4)-(6)and has the analytical solutions

where 0≤x1,x2≤ 2π.Calculations are carried out for k=2 on a set of uniform grid,{11×11,21×21,...,51×51}.A f i xed time step∆t=0.002 and Re=100 are employed.Numerical solutions are computed at t=2.The exact solution,i.e.equations(66)-(68),providestheinitialf i eldatt=0andthetime-dependentboundaryconditions.Table1showstheaccuracycomparisonbetweenthepresentscheme and compact FDM scheme of Tian,Liang,and Yu(2011)in terms of RMS errors and convergence rates.It is seen that the present scheme produces better accuracy and better convergence rates than the scheme of Tian,Liang,and Yu(2011),i.e.O(h5.35)compared to O(h2.92)for the velocity and O(h4.48)compared to O(h3.28)for the pressure.
5.4 Taylor-Green vortex in non-rectangular domain
In order to analyse the performance of the combination of the fully coupled approach and CIRBF approximation scheme in solving the transient viscous f l ow in a non-rectangular domain,we consider the case of an array of decaying vortices with the analytical solutions[Uhlmann(2005)]described by

The f l ow is computed in an embedded circular domain with radius of unity and centred at the origin of the computational domain Ω =[−1.5,1.5]× [−1.5,1.5].The interior nodes are chosen and the boundary nodes are generated in a similar manner described in Section 5.2.Calculations are carried out on a set of uniform grids,{10×10,20×20,...,50×50}.The Reynolds number is set to be Re=5 and numerical solutions are computed at t=0.3 using a f i xed time step∆t=0.001.The initial f i eld at t=0 and the time-dependent boundary conditions are given by(69)-(71).Table 2 illustrates the accuracy comparison between the present scheme and FDM approach of Uhlmann(2005)in terms of maximum errors and convergence rates.It is observed that present scheme produces lower errors with better convergence rates,i.e.O(h4.44)for the u-velocity and O(h4.59)for the v-velocity in comparison with O(h2.13)for both u-and v-velocities given by the approach of Uhlmann(2005).
5.5 Lid driven cavity f l ow
The classical lid driven cavity f l ow has been considered as a test problem for the evaluation of numerical methods and the validation of f l uid f l ow solvers for the past decades.Figure 8 shows the problem def i nition and boundary conditions.Uniform grids of{31×31,51×51,71×71,91×91,111×111,129×129}and a range of Re∈{100,400,1000,3200}are employed in the simulation.A f i xed time step is chosen to be∆t=0.001.Results of the present scheme are compared with those of some others[Ghia,Ghia,and Shin(1982);Gresho,Chan,Lee,and Upson(1984);Bruneau and Jouron(1990);Deng,Piquet,Queutey,and Visonneau(1994b);Botella and Peyret(1998);Sahin and Owens(2003);Thai-Quang,Le-Cao,Mai-Duy,and Tran-Cong(2012)].From the literature,FDM results using very dense grids presented by Ghia,Ghia,and Shin(1982)and pseudo-spectral results presented by Botella and Peyret(1998)have been referred to as"Benchmark"results for comparison purposes.

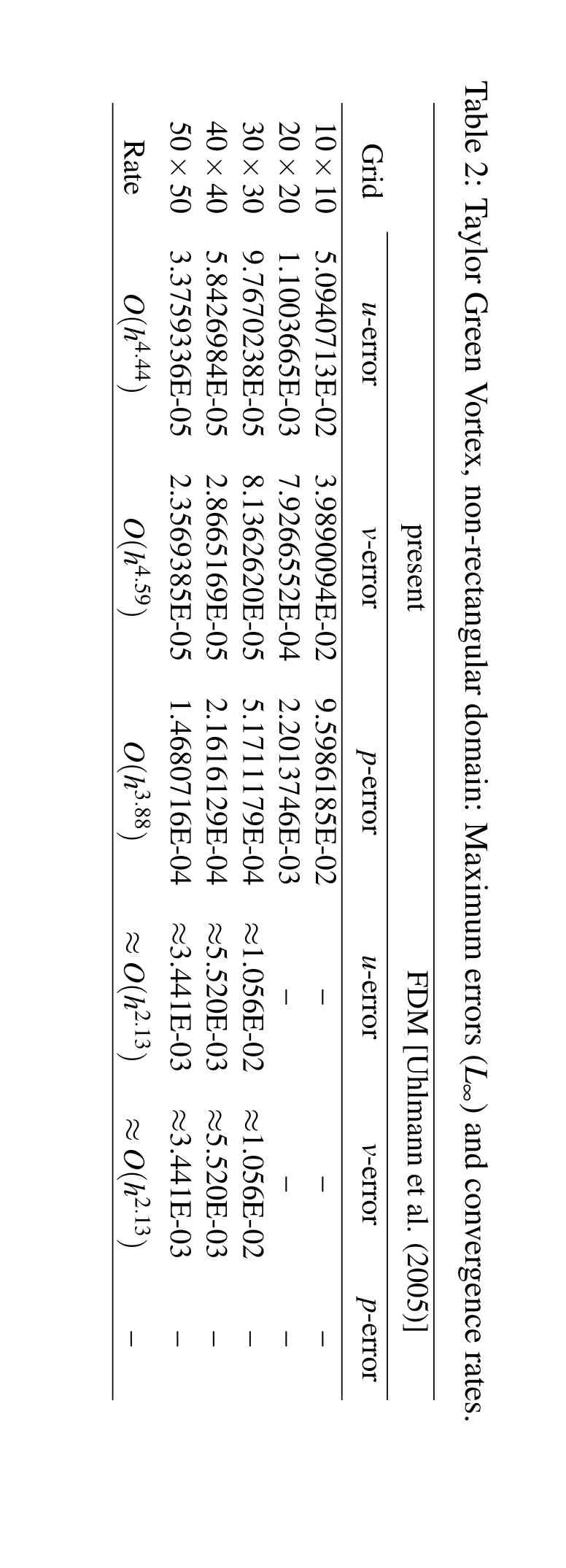

Figure 8:Lid driven cavity:problem conf i guration and boundary conditions.
Tables 3,4,5,and 6 show the present results for the extrema of the vertical and horizontal velocity prof i les along the horizontal and vertical centrelines of the cavity for several Reynolds numbers.For Re=100(Table 3)and Re=1000(Table 4),the"Errors"are evaluated relative to"Benchmark"results of Botella and Peyret(1998).The results obtained by the present scheme are very comparable with others.
Figure 9 displays velocity prof i les along the vertical and horizontal centrelines for different grid sizes at Re=1000,where a grid convergence of the present scheme is obviously observed(i.e.the present solution approaches the benchmark solution with a fast rate as the grid density is increased).The present scheme effectively achieves the benchmark results with a grid of only 91×91 in comparison with the grid of 129×129 used to obtain the benchmark results in[Ghia,Ghia,and Shin(1982)].In addition,those velocity prof i les at Re∈{100,400,1000,3200}with the grid size of{51×51,71×71,91×91,129×129},respectively,are displayed in Figure 10,where the present solutions match the benchmark ones very well.



91×91-0.328548 0.2800 0.303655 0.2254-0.453936 0.8623 CIRBF(u,v,p),[Thai-Quang(2012b)]51×51-0.323158 0.2814 0.297493 0.2248-0.442770 0.8605 CIRBF(u,v,p),[Thai-Quang(2012b)]71×71-0.325168 0.2804 0.300818 0.2252-0.449146 0.8620 FVM(u,v,p),[Deng(1994b)] 128×128-0.32751— 0.30271— -0.45274—FDM(ψ−ω),[Ghia(1982)] 129×129-0.32726 0.2813 0.30203 0.2266-0.44993 0.8594 FVM(u,v,p),[Sahin(2003)] 257×257-0.328375 0.2815 0.304447 0.2253-0.456316 0.8621 71×71-0.328095 0.2801 0.303156 0.2257-0.453380 0.8622 Present 51×51-0.325864 0.2809 0.300815 0.2265-0.450157 0.8619 Present Present Method Grid umin ymin vmax xmax vmin xmin able 5:Lid driven cavity,Re=400:Extrema of the vertical and horizontal velocity prof i les along the horizontal and vertical ntrelines of the cavity,respectively.

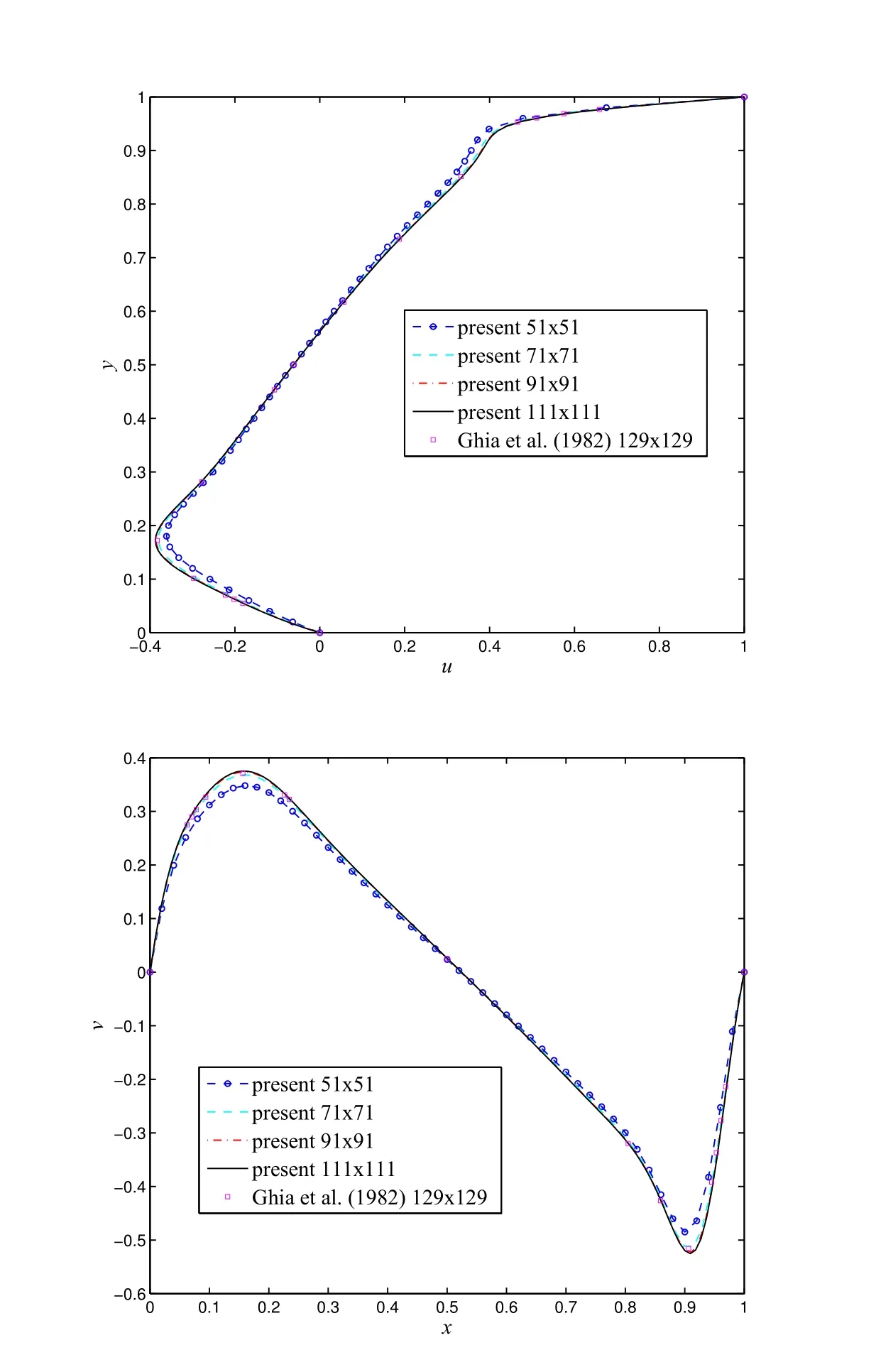
Figure 9:Lid driven cavity,Re=1000:Prof i les of the u-velocity along the vertical centreline and the v-velocity along the horizontal centreline as grid density increases.It is noted that the curves for the last two grids are indistinguishable and in good agreement with the benchmark results of[Ghia,Ghia,and Shin(1982)].
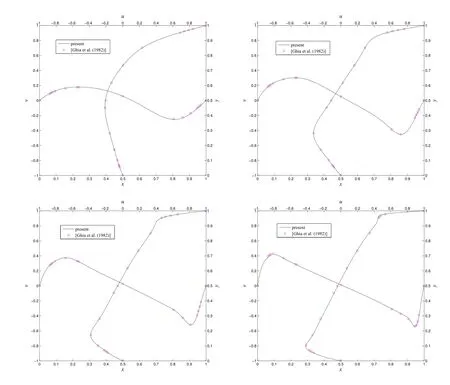
Figure 10:Lid driven cavity:Prof i les of the u-velocity along the vertical centreline and the v-velocity along the horizontal centreline for Re=100(top-left),Re=400(top-right),Re=1000(bottom-left),and Re=3200(bottom-right)with the grid of 51×51,71×71,91×91,and 129×129,respectively.
To exhibit contour plots of the f l ow,a range of Re∈{100,400,1000,3200}and the grid of{51×51,71×71,91×91,129×129}are employed,respectively.Figures 11 and 12 show streamlines and iso-vorticity lines,which are derived from the velocity f i eld.Figure 13 shows the pressure deviation contours of the present simulations.These plots are also in good agreement with those reported in the literature.

Figure 11:Lid driven cavity:Streamlines of the f l ow for Re=100(top-left),Re=400(top-right),Re=1000(bottom-left),and Re=3200(bottom-right)with the grid of 51×51,71×71,91×91,and 129×129,respectively.The contour values used here are taken to be the same as those in[Ghia,Ghia,and Shin(1982)].
5.6 Irregular bottom lid driven cavity

Figure 12:Lid driven cavity:Iso-vorticity lines of the f l ow for Re=100(top-left),Re=400(top-right),Re=1000(bottom-left),and Re=3200(bottom-right)with the grid of 51×51,71×71,91×91,and 129×129,respectively.The contour values used here are taken to be the same as those in[Ghia,Ghia,and Shin(1982)].
The lid driven cavity with a deformed base presented in[Udaykumar,Shyy,and Rao(1996);Shyy,Udaykumar,Rao,and Smith(1996)]is chosen to validate the performance of the present fl uid fl ow solver in an irregular domain.The base is deformed sinusoidally with an amplitude of 10 percent of the base.The computational domain and boundary conditions are illustrated in Figure 14.The interior and boundary nodes are generated in a similar manner described in Section 5.2.The spatial discretisation is shown in Figure 15.A range of uniform grids,{53×53,63×63,83×83,93×93}is employed in the simulation.A f i xed time stepandReynolds numberarechosento be∆t=0.001and Re=1000,respectively.The results from the present method are compared with those presented in[Shyy,Udaykumar,Rao,and Smith(1996);Mariani and Prata(2008)],where appropriate.From the literature,the FVM(Finite Volume Method)results using the well-tested body-f i tted coordinate formulation and dense grid of 121×121 presented in[Shyy,Udaykumar,Rao,and Smith(1996)]have been considered as"Benchmark"results for comparison purposes.

Figure 13:Lid driven cavity:Static pressure contours of the f l ow for Re=100(top-left),Re=400(top-right),Re=1000(bottom-left),and Re=3200(bottomright)with the grid of 51×51,71×71,91×91,and 129×129,respectively.The contour values used here are taken to be the same as those in[Abdallah(1987)]for Re=100 and Re=400,[Botella and Peyret(1998)]for Re=1000,and[Bruneau and Saad(2006)]for Re=3200.
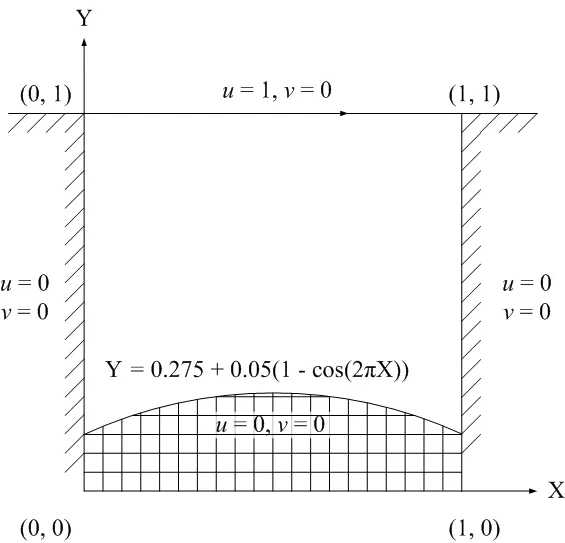
Figure 14:Irregular bottom lid driven cavity:problem conf i guration and boundary conditions.

Figure 15:Irregular bottom lid driven cavity,spatial discretisation:+,interior nodes;◦,boundary nodes.
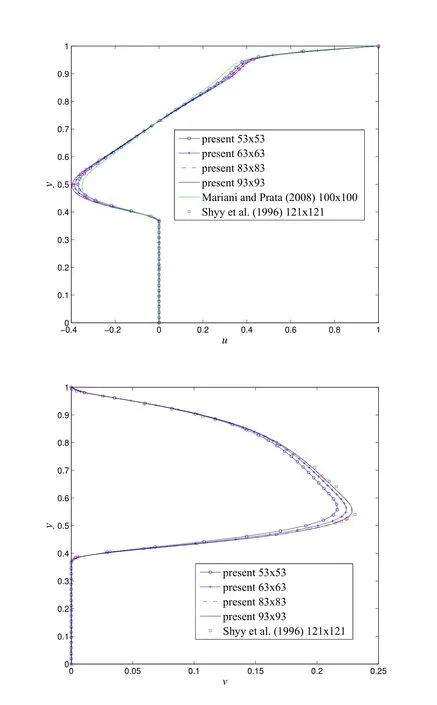
Figure 16:Irregular bottom lid driven cavity,Re=1000:Prof i les of the u-velocity(top)and v-velocity(bottom)along the vertical centreline as grid density increases.It is noted that the curves for the last two grids are indistinguishable and in good agreementwiththebenchmarkresultsofShyy,Udaykumar,Rao,andSmith(1996).

Figure 17:Irregular bottom lid driven cavity:Streamlines of the f l ow for Re=1000 with the grid of 83×83.The plot contains 30 contour lines whose levels vary linearly from the minimum to maximum values;and,it is in good agreement with that of Shyy,Udaykumar,Rao,and Smith(1996).

Figure 18:Irregular bottom lid driven cavity:Static pressure contours of the f l ow for Re=1000 with the grid of 83×83.The plot contains 160 contour lines whose levels vary linearly from the minimum to maximum values.
Figure 16 displays horizontal and vertical velocity prof i les along the vertical centreline for different grid sizes at Re=1000,where a grid convergence of the present scheme is obviously observed(i.e.the present solution approaches the benchmark solution with a fast rate as the grid density is increased).The present scheme effectively achieves the benchmark results with a grid of only 83×83 in comparison with the grid of 121×121 used to obtain the benchmark results in[Shyy,Udaykumar,Rao,and Smith(1996)].In addition,the present results with a grid of only 53×53 outperform those of Mariani and Prata(2008)using the grid of 100×100.To exhibit contour plots of the f l ow,we employ the grid of 83×83 for Re=1000.Figure 17 shows streamlines which are derived from the velocity f i eld.Figure 18 shows the pressure deviation contours of the present simulation.These plots are in close agreement with those reported in the literature.
6 Concluding remarks
In this paper,we implement the high-order compact integrated radial basis function(CIRBF)scheme,where fi rst-and second-order derivative values of the fi eld variables are included,in combination with the direct fully coupled velocity-pressure approach in the Cartesian-grid point-collocation structure.Like FDMs,the present approximation technique involves 3 nodes in each direction,which results in a sparse system matrix.Numerical examples indicate that the results of the present scheme are superior to those of the standard FDM scheme and second-and fourthorder compact FDM schemes in terms of solution accuracy and convergence rates with grid re fi nement.It is shown that the CIRBF scheme has at least fourth-order accuracy when approximating the Poisson equations in either rectangular or nonrectangular domains.The combination of the CIRBF and the direct fully coupled approach maintains the fourth-order accuracy in solving the transient fl ow problems of Taylor-Green vortices in rectangular/non-rectangular domains.In the fl uid fl ow simulations with regular/irregular boundaries,the numerical results obtained by the present approach are highly accurate and in good agreement with the reported results in the literature.
Acknowledgement: Thef i rstauthorwouldliketothankUSQforanInternational Postgraduate Research Scholarship.The authors would like to thank the reviewers for their helpful comments.
Abdallah,S.(1987): Numerical solutions for the incompressible Navier-Stokes equations in primitive variables using a non-staggered grid,Part II.J.Comput.Phys.,vol.70,pp.193–202.
Acharya,S.;Baliga,B.;Karki,K.;Murthy,J.;Prakash,C.;Vanka,S.(2007):Pressure-based fi nite-volume methods in computational fl uid dynamics.J.Heat Transfer,vol.129,pp.407–424.
Ammara,I.;Masson,C.(2004):Development of a fully coupled control-volume fi nite element method for the incompressible Navier-Stokes equations.Int.J.Numer.Meth.Fluids,vol.44,pp.621–644.
Botella,O.;Peyret,R.(1998): Benchmark spectral results on the lid-driven cavity fl ow.Comput.Fluids,vol.27,no.4,pp.421–433.
Braaten,M.;Patankar,S.(1990): Fully coupled solution of the equations for incompressible recirculating fl ows using a penalty-function fi nite-difference formulation.Comput.Mech.,vol.6,pp.143–155.
Braaten,M.;Shyy,W.(1986):Comparison of iterative and direct solution methods for viscous fl ow calculations in body- fi tted co-ordinates.Int.J.Numer.Meth.Fluids,vol.6,pp.325–349.
Bruneau,C.;Jouron,C.(1990):An ef fi cient scheme for solving steady incompressible Navier-Stokes equations.J.Comput.Phys.,vol.89,pp.389–413.
Bruneau,C.;Saad,M.(2006): The 2D lid-driven cavity problem revisited.Comput.Fluids,vol.35,pp.326–348.
Caretto,L.;Curr,R.;Spalding,D.(1972): Two numerical methods for threedimensional boundary layers.Comput.Method.Appl.Mech.and Engrg.,vol.1,pp.39–57.
Darwish,M.;Sraj,I.;Moukalled,F.(2009):A coupled fi nite volume solver for the solution of incompressible fl ows on unstructured grids.J.Comput.Phys.,vol.228,pp.180–201.
Deng,G.;Piquet,J.;Queutey,P.;Visonneau,M.(1994a):A new fully coupled solution of the Navier-Stokes equations.Int.J.Numer.Meth.Fluids,vol.19,pp.605–639.
Deng,G.;Piquet,J.;Queutey,P.;Visonneau,M.(1994b): Incompressiblefl ow calculations with a consistent physical interpolation fi nite-volume approach.Comput.Fluids,vol.23,no.8,pp.1029–1047.
Elman,H.;Howle,V.;Shadid,J.;Tuminario,R.(2003): A parallel block multi-level preconditioner for the 3D incompressible Navier-Stokes equations.J.Comput.Phys.,vol.187,pp.504–523.
Fasshauer,G.(2007): Meshfree approximation methods with Matlab.World Scienti fi c Publishing,5 Toh Tuck Link,Singapore 596224.
Furuichi,M.;May,D.;Tackley,P.(2011):Development of a Stokes fl ow solver robust to large viscosity jumps using a Schur complement approach with mixed precision arithmetic.J.Comput.Phys.,vol.230,pp.8835–8851.
Galpin,P.;Doormaal,J.V.;Raithby,G.(1985):Solution of the incompressible mass and momentum equations by application of a coupled equation line solver.Int.J.Numer.Meth.Fluids,vol.5,pp.615–625.
Gamet,L.;Ducros,F.;Nicoud,F.;Poinsot,T.(1999):Compact fi nite difference schemes on non-uniform meshes.Application to direct numerical simulations of compressible fl ows.Int.J.Numer.Meth.Fluids,vol.29,pp.159–191.
Ghia,U.;Ghia,K.;Shin,C.(1982):High-resolutions for incompressible fl ows using Navier-Stokes equations and a multigrid method.J.Comput.Phys.,vol.48,pp.387–411.
Gresho,P.;Chan,S.;Lee,R.;Upson,C.(1984): A modi fi ed fi nite element method for solving the time-dependent,incompressible Navier-Stokes equations.Part 2:Applications.Int.J.Numer.Meth.Fluids,vol.4,pp.619–640.
Hanby,R.;Silvester,D.;Chew,J.(1996):A comparison of coupled and segregated iterative solution techniques for incompressible swirling fl ow.Int.J.Numer.Meth.Fluids,vol.22,pp.353–373.
Henniger,R.;Obrist,D.;Kleiser,L.(2010): High-order accurate solution of the incompressible Navier-Stokes equations on massively parallel computers.J.Comput.Phys.,vol.229,pp.3543–3572.
Kansa,E.(1990a): Multiquadrics-A scattered data approximation scheme with applications to Computational Fluid-Dynamics-I.Surface approximations and partial derivative estimates.Computers Math.App fi c.,vol.19,no.8/9,pp.127–145.
Kansa,E.(1990b): Multiquadrics-A scattered data approximation scheme with applications to Computational Fluid-Dynamics-II.Solutions to parabolic,hyperbolic and elliptic partial differential equations.Computers Math.App fi c.,vol.19,no.8/9,pp.147–161.
Karki,K.;Mongia,H.(1990): Evaluation of a coupled solution approach for fl uid fl ow calculations in body- fi tted co-ordinates.Int.J.Numer.Meth.Fluids,vol.11,pp.1–20.
Mai-Duy,N.;Tanner,R.(2007):Acollocationmethodbasedonone-dimensional RBF interpolation scheme for solving PDEs.Int.J.Numer.Meth.Heat Fluid Flow,vol.17,no.2,pp.165–186.
Mai-Duy,N.;Tran-Cong,T.(2001a): Numerical solution of differential equations using multiquadric radial basis function networks.Neural Networks,vol.14,pp.185–199.
Mai-Duy,N.;Tran-Cong,T.(2001b): Numerical solution of Navier-Stokes equations using multiquadric radial basis function networks.Int.J.Numer.Meth.Fluids,vol.37,pp.65–86.
Mai-Duy,N.;Tran-Cong,T.(2003):Approximation of function and its derivatives using radial basis function networks.Appl.Math.Modell.,vol.27,pp.197–220.
Mai-Duy,N.;Tran-Cong,T.(2005):An ef fi cient indirect RBFN-based method for numerical solution of PDEs.Numer.Methods Partial.Diff.Equations,vol.21,no.4,pp.770–790.
Mai-Duy,N.;Tran-Cong,T.(2007):A Cartesian-grid collocation method based on radial basis-function networks for solving PDEs in irregular domains.Numer.Methods Part.Differ.Eqs.,vol.23,pp.1192–1210.
Mai-Duy,N.;Tran-Cong,T.(2010):A numerical study of 2D integrated RBFNs incorporating Cartesian grids for solving 2D elliptic differential problems.Numer.Methods Part.Differ.Eqs.,vol.26,no.6,pp.1443–1462.
Mai-Duy,N.;Tran-Cong,T.(2013): A compact fi ve-point stencil based on integrated RBFs for 2D second-order differential problems.J.Comput.Phys.,vol.235,pp.302–321.
Mariani,V.;Prata,A.(2008): A Eulerian-Lagrangian method applied to fl uid fl ow in lid-driven cavities with irregular bottom walls.Numer.Heat Tr.B-Fund.,vol.53,pp.206–233.
May,D.;Moresi,L.(2008): Preconditioned iterative methods for Stokes fl ow problems arising in computational geodynamics.Phys.Earth Planet.In.,vol.171,pp.33–47.
Mazhar,Z.(2001): A procedure for the treatment of the velocity-pressure coupling problem in incompressible fl uid fl ow.Numer.Heat Tr.B-Fund.,vol.39,pp.91–100.
Moin,P.;Kim,J.(1980):On the numerical solution of time-dependent viscous incompressible fl uid fl ows involving solid boundaries.J.Comput.Phys.,vol.35,pp.381–392.
Pascau,A.;Perez,C.(1996):A comparison of segregated and coupled methods for the solution of the incompressible Navier-Stokes equations.Commun.Numer.Meth.Engrg.,vol.12,pp.617–630.
Patankar,S.;Spalding,D.(1972): A calculation procedure for heat,mass and momentum transfer in three-dimensional parabolic fl ows.Int.J.Heat Mass Transfer,vol.15,pp.1767–1806.
Perot,J.(1993): An analysis of the fractional step method.J.Comput.Phys.,vol.108,pp.51–58.
Sahin,M.;Owens,R.(2003):Anovelfullyimplicitf i nitevolumemethodapplied to the lid-driven cavity problem-Part I:High Reynolds number f l ow calculations.Int.J.Numer.Meth.Fluids,vol.42,pp.57–77.
Shyy,W.;Udaykumar,H.;Rao,M.;Smith,R.(1996): Computational f l uid dynamics with Moving boundaries.Taylor&Francis,1900 Frost Road,Suite 101,Bristol,PA 19007-1598.
Silvester,D.;Elman,H.;Kay,D.;Wathen,A.(2001):Eff i cient preconditioning of the linearized Navier-Stokes equations for incompressible f l ow. J.Comput.Appl.Math.,vol.128,pp.261–279.
Thai-Quang,N.;Le-Cao,K.;Mai-Duy,N.;Tran-Cong,T.(2012): A highorder compact local integrated-RBF scheme for steady-state incompressible viscous f l ows in the primitive variables.CMES:Computer Modeling in Engineering and Sciences,vol.84,no.6,pp.528–557.
Thai-Quang,N.;Mai-Duy,N.;Tran,C.-D.;Tran-Cong,T.(2012):High-order alternating direction implicit method based on compact integrated-RBF approximations for unsteady/steady convection-diffusion equations. CMES:Computer Modeling in Engineering and Sciences,vol.89,no.3,pp.189–220.
Tian,Z.;Liang,X.;Yu,P.(2011): A higher order compact f i nite difference algorithm for solving the incompressible Navier-Stokes equations.Int.J.Numer.Meth.Engng.,vol.88,no.6,pp.511–532.
Udaykumar,H.;Shyy,W.;Rao,M.(1996): ELAFINT:A mixed Eulerian-Lagrangian method for f l uid f l ows with complex and moving boundaries.Int.J.Numer.Meth.Fluids,vol.22,pp.691–712.
Uhlmann,M.(2005):An immersed boundary method with direct forcing for the simulation of particular f l ows.J.Comput.Phys,vol.209,pp.448–476.
Vanka,S.(1986a):Block-implicit multigrid solution of Navier-Stokes equations in primitive variables.J.Comput.Phys.,vol.65,pp.138–158.
Vanka,S.(1986b):A calculation procedure for three-dimensional steady recirculating f l ows using multigrid methods.Comput.Method.Appl.Mech.and Engrg.,vol.55,pp.321–338.
Zedan,M.;Schneider,G.(1985): A coupled strongly implicit procedure for velocity and pressure computation in f l uid f l ow problems.Numer.Heat Transfer,vol.8,pp.537–557.
1Computational Engineering and Science Research Centre,Faculty of Health,Engineering and Sciences,The University of Southern Queensland,Toowoomba,Queensland 4350,Australia.
杂志排行
Computer Modeling In Engineering&Sciences的其它文章
- A Fast Multipole Accelerated Singular Boundary Method for Potential Problems
- Three Dimensional Natural Frequency Analysis of Sandwich Plates with Functionally Graded Core Using Hybrid Meshless Local Petrov-Galerkin Method and Artif i cial Neural Network
- CMES: Computer Modeling in Engineering & Sciences
