Three Dimensional Natural Frequency Analysis of Sandwich Plates with Functionally Graded Core Using Hybrid Meshless Local Petrov-Galerkin Method and Artif i cial Neural Network
2015-12-19FoadNazariMohammadHosseinAbolbashariandSeyedMahmoudHosseini
Foad Nazari,Mohammad Hossein Abolbashari,2 and Seyed Mahmoud Hosseini
Three Dimensional Natural Frequency Analysis of Sandwich Plates with Functionally Graded Core Using Hybrid Meshless Local Petrov-Galerkin Method and Artif i cial Neural Network
Foad Nazari1,Mohammad Hossein Abolbashari1,2and Seyed Mahmoud Hosseini3
Present study is concerned with three dimensional natural frequency analysis of functionally graded sandwich rectangular plates using Meshless Local Petrov-Galerkin(MLPG)method and Artif i cial Neural Networks(ANNs).The plate consists of two homogeneous face sheets and a power-law FGM core.Natural frequencies of the plate are obtained by 3D MLPG method and are verif i ed with available references.Convergence study of the f i rst four natural frequencies for different node numbers is the next step.Also,effects of two parameters of“FG core to plate thickness ratio”and “volume fraction index”on natural frequencies of plate are investigated.Then,four distinct ANNs are used to predict the f i rst four natural frequencies of the plate.Back-Error Propagation(BEP)method is used to train the ANNs.The predicted data shows a good agreement with respect to the actual data.Finally,the trained ANNs are used for prediction of natural frequencies of some conditions where MLPG data are not available.
Natural Frequency,Sandwich Plate with FG Core,Hybrid MLPG&ANN.
1 Introduction
Functionally graded materials(FGMs)are a new generation of materials consists of two or more constituent phases with a smoothly varying composition of gradually changingthevolume fractionofthematerials.Theyoffersuperiorthermal-resistantproperties in comparison to conventional composites.Vibration analysis of FGM structures has been the focus of many researchers.Praveen and Reddy(1998)and Loy,Lam and Reddy(1999)studied the vibration of 2D FGM structures.Cheng and Batra(2000)applied Reddy’s third-order shear deformation theory to investigate the steady state vibrations of a simply supported FGM plate resting on an elastic foundation.Furthermore,Vel and Batra(2004)presented an exact 3D solution for free and forced vibrations of rectangular FGM plates.In another study,Batra and Jin(2005)studied the FGM anisotropic plates with various boundary conditions by applying the f i nite element method and f i rst-order shear deformation theory.Ferreira,Batra,Roque,Qian,Jorge(2006)and Roque,Ferreira,Jorge(2007)presented a meshless method based on radial basis functions for solving the free vibration problem of FG plates.Matsunaga(2008)performed a dynamic and stability analysis of simply supported edges FGM plates using several sets of 2D advanced approximate theories.Hosseini and Abolbashari(2010)presented an analytical method for dynamic response analysis of FG thick hollow cylinders under impact loading.They analytically solved the wave motion equation based on the composition of Bessel functions.Furthermore,Iqbal,Muhammad,and Nazra(2009)applied wave propagation approach to study the vibration characteristics of FG cylindrical shells.
One of the important structural FG constructions that has been studied in the recent years are sandwich FG plates.Buckling and free vibration of sandwich plates with FGM face sheets was studied by Zenkour(2005).His study was based on a sinusoidal shear deformation plate theory.In another paper,a 3D Ritz analysis of sandwich FG plates of two types:plates with FGM face sheets and homogeneous core and plates with homogeneous face sheets and a FGM core was presented by Li,Iu and Kou(2008).In an interesting study,Neves,Ferreira,Carrera,Cinefra,Roque,Jorge and Soares(2013)investigated the static,dynamic and stability analysis of sandwich FGM using a quasi-3D higher-order shear deformation theory.Meanwhile,Dozio(2013)developed advanced 2D Ritz-based models for accurate prediction of natural frequencies of thin and thick sandwich plates with FG core.The meshless local Petrov–Galerkin(MLPG)method developed by Atluri and his co-workers[Atluri and Zhu(1998);Atluri,Kim and Cho(1999);Atluri and Zhu(2000);Atluri and Shen(2002)]is based on the local weak instead of global weak formulation of the problem.In an interesting review paper,Sladeak,Stanak,Han,Sladek and Atluri(2013)investigated recent studies that have been performed using MLPG method in different engineering and science f i elds.Furthermore,Sladek,Sladek and Solek(2009)applied MLPG to study the transient heat conduction problems in 3D solids with continuously non-homogeneous and anisotropic material properties.Sladek,Sladek,Tan,and Atluri(2008)also studied the tran-sient heat conduction in 3D anisotropic functionally graded solids using MLPG method.In another work Sladek,Sladek,Zhang,Solek,and Starek(2007)applied MLPG to fracture analysis in continuously nonhomogeneous piezoelectric solids.Furthermore,MLPG method was used to stress and crack analyses in 3-D axisymmetric FGM bodies by Sladek,Sladek,Krivacek,and Zhang(2005).MLPG method was utilized for transient linear thermoelastic analysis by Sladek,Sladek,Solek,Tan,and Zhang(2009).In that paper they considered orthotropic material properties for the structure.A thermo-elastic wave propagation analysis was performed based on the Green-Naghdi coupled thermo-elasticity in a functionally graded thick hollow cylinder considering uncertainty in constitutive mechanical properties under thermal shock loading by Hosseini,Shahabian,Sladek and Sladek(2011).They developed MLPG method accompanied with Monte-Carlo simulation to solve the stochastic boundary value problem.Moreover,MLPG method was exploited by Ghouhestani,Shahabian,and Hosseini(2014)for dynamic analysis of functionally graded nanocomposite cylindrical layered structure reinforced by carbon nanotube subjected to mechanical shock loading.In that study,the carbon nanotubes(CNTs)were assumed to be distributed across radial direction on thickness of cylinder,which can be simulated by linear and nonlinear volume fraction.They studied free vibration and elastic wave propagation for various volume fraction exponent values at various time intervals.Liu,Long,and Li.(2008)developed MLPG method for crack analysis in the isotropic functionally graded material.Furthermore,Zhang,Dong,Alotaibi and Atluri(2013)applied a simple MLPG Mixed-Collocation method for analyzing linear isotropic/anisotropic elasticity with simply/multiply-connected domains.Zhang,He,Yong,Li,Alotaibi and Atluri(2014)developed the MLPG Mixed Collocation method to solve the Cauchy inverse problems of steady-state heat transfer.They applied the mixed scheme to independently interpolate temperature as well as heat f l ux using the same meshless basis functions.The balance and compatibility equations were satisf i ed strongly at each node using the collocation method.Moreover,Long and his co-workers[Dong and Atluri,(2012);Dong and Atluri(2011);Dong and Atluri(2012);Dong,El-Gizawy,Juhany and Atluri(2014);Bishay,Dong,and Atluri(2014);Dong,El-Gizawy,Juhany,Atluri(2014)]presented some interesting simple methods for analyzing laminated composite,functionally graded and heterogeneous materials.Sladek,Sladek and Zhang(2005)studied 2D static and dynamic deformations of FG solids using MLPG method.Qiana,Batra and Chena(2004)and Gilhooley,Batra,Xiao,McCarthy and Gillespie(2007)applied a higher-order shear and normal deformable plate theory and the MLPG method to investigate the static and dynamic deformations of thick FGM plates.In another study,Rezaei Mojdehi Darvizeh,Basti and Rajabi(2011)presented the static and dynamic analysis of thick FG plates using MLPG method.Hosseini(2014)applied a hybrid technique based on composition of Newmark fi nite difference and MLPG methods for natural frequencies analysis of a thick FG cylinder.Moussavinezhad,Shahabian,and Hosseini(2013)investigated the propagation of elastic wave in two dimensional functionally graded thick hollow cylinder with fi nite length subjected to mechanical shock loading,considering 2D variations for mechanical properties using MLPG method to solve the boundary value problem.In another study Avila,Han and Atluri(2011)applied a novel MLPG fi nite volume mixed method for analyzing Stokesian fl ows&study of a new vortex mixing fl ow.This method is based on independent interpolation of the pressure,the deviatoric velocity strain tensor,the volumetric velocity strain tensor and the velocity vector.Also Godinho and Dias-da-Costa(2013)proposed the MLPG method for transient heat transfer in frequency domain.In this study 5thversion of MLPG method was applied
Ontheotherhand,theconceptofANNintherecentyearshasattractedtheattention of many researchers in broad areas.Speci fi cally,some interesting studies have been conducted about the vibration of FG structures using ANN.Jodaei,Jalal and Yas(2012)applied ANN technique for 3D analysis of exponentially FG annular plates by using state-space based differential quadrature method(SSDQM)for different boundary conditions.In another study,Jodaei,Jalal and Yas(2013)also investigated the free vibration analysis of FG piezoelectric annular plates by employing SSDQM and ANN.Also Kamarian,Yas,and Pourasghar(2013)applied Imperialist Competitive Algorithm(ICA),ANN and Genetic Algorithm(GA)to optimize the volume fraction of FG beams resting on elastic foundation for maximizing the fi rst natural frequency.
In this study,hybrid MLPG and ANN methods are used for parametric analysis of 3D natural frequency analysis of sandwich rectangular plates with FG core.
2 Problem Def i nition
2.1 Geometrical conf i guration
In this study,the considered structure is a rectangular FGM sandwich plate with uniform thickness which composed of three elastic layers from bottom to top(Homogeneous face sheets and a FGM core).A schematic 3D view of the plate and the Cartesian coordinates(x1,x2,x3)are shown in Fig.1.The thicknesses of top and bottom layers are equal.As illustrated in Fig.1,h/H is the ratio of core layer thickness to the plate thickness which is varying from 0.1 to 0.9 in this study.

Figure 1:A Schematic3D view of the rectangular FGM sandwich plate.
2.2 Material properties
A schematic 2D view of the considered rectangular FGM sandwich plate and the rectangular Cartesian coordinates are shown in f i gure 2.As illustrated in this f i gure,plate composed of two homogeneous face-sheets on the bottom and top of a FG core.
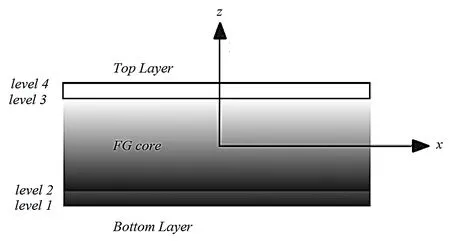
Figure 2:A schematic 2D view of the rectangular FGM sandwich plate.
In order to describe the FGM variation of material properties,power-law function is a common pattern.For the FG core of the considered FGM sandwich plate thedensity and elasticity modulus are assumed to vary continuously in the thickness direction only due to gradually changing of the volume fraction of the constituent materials.Furthermore,the Poisson’s ratio assumed to be constant.Along the thickness direction of the FG core,volume fraction function is denoted by s and assumed to obey the following formula:
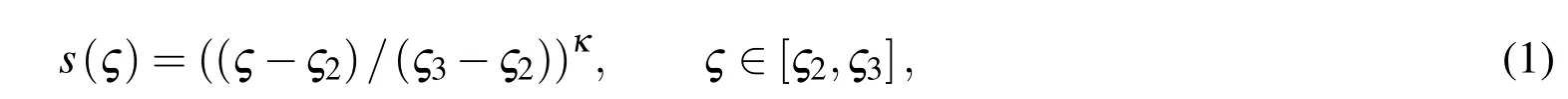
where κ is the volume fraction index of power-law pattern and ςj=hj/H,(j=1,2,3,4).
Inaddition,accordingtoequation(2),amixturerulecomposedofYoung’smodulus and mass density is used to express the effective material properties of the plate along the thickness.

In equation(2),λeff,λ1and λ4are the effective material properties of FG core,the properties of the top and bottom layers,respectively.
3 MLPG formulation
Equation(3)gives the 3D equation of motion in the domain of volume Ω that is bounded by the surface Γ.


where uirepresents the displacement component and tirepresents the surface traction components.¯uiand¯tiare the prescribed displacement and prescribed traction on Γuand Γt,respectively.Also,the unit outward vector normal to boundary Γtis presented by nj.
Over the local sub-domains, the weak formulation inside the global domain Ω is constructed.
As can be seen in Fig. 3, brick-shaped local domains in this study are considered as sub-domains and support domains. Because the global domain of the rectangular plate is hexahedral, the mapping procedure becomes simple and no special treatment is needed when the local sub-domain intersects the global boundary.

Figure 3: Sub-domains and global domain of a rectangular plate.
3.1 Local symmetric weak form
As this paper deals with the free vibration analysis, the body force vector is assumed to be zero. Therefore, over a local sub-domain around node i, the generalized local weak form of the equilibrium equations can be written as:
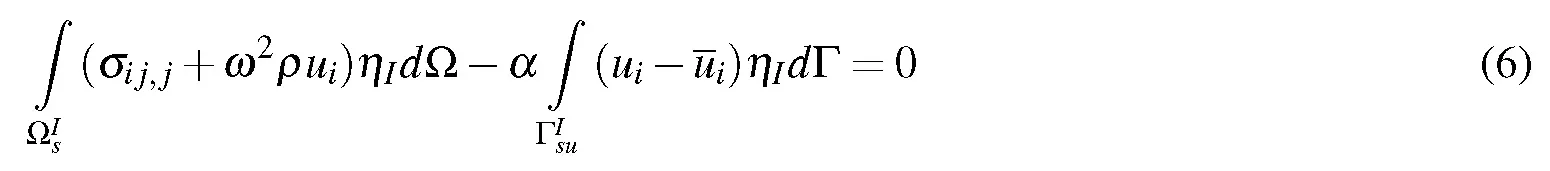
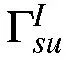
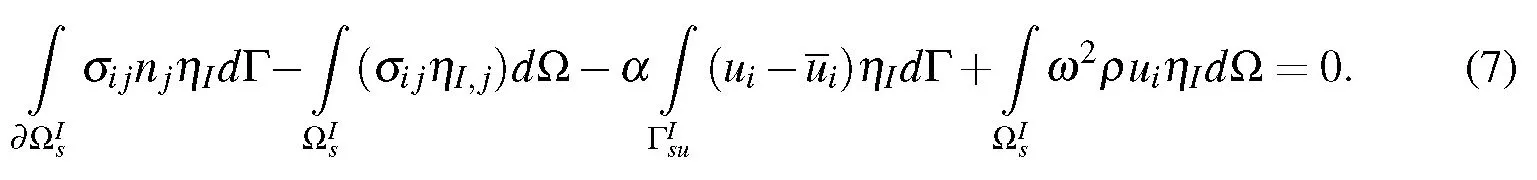
The boundary of local sub-domainconsists of three parts,this equationis a part of local boundary which is placed inside the global domain.It does not have any contact with the problems’global boundary.Furthermore,andare parts of the local boundary that coincide with the global traction and displacement boundaries,respectively.As=0,equation(7)is converted to
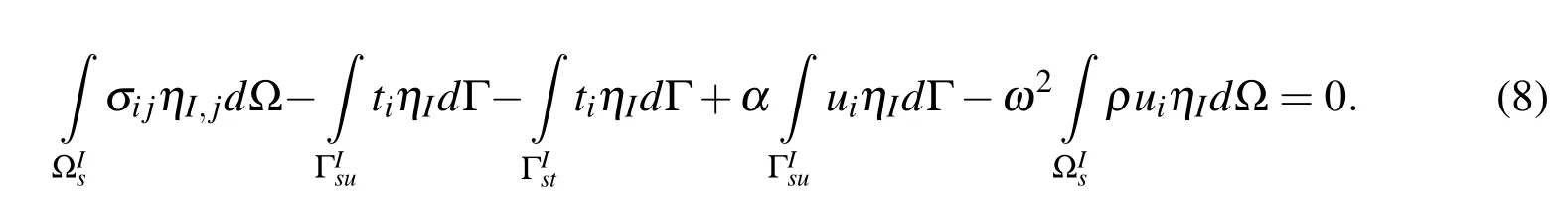
This equation is the symmetric local weak form of linear elastic free vibration.It should be mentioned that ηI(x)should be chosen such that to be vanished outside the Ωs,and to be positive inside the Ωs.
3.2 Moving least square approximation
In Moving Least Square(MLS)approximation the unknown trial approximant u∗(x)of the function u(x)is def i ned as:

In this equation,pT=[p1(x),p2(x),p3(x),...,pm(x)]is a complete monomial basis of order m.Meanwhile,Ωxis the def i ned domain of MLS approximation at point x for the trial function.For 3D problems the quadratic basis vector pTcould be def i ned as:

Minimization of a weighted discrete L2norm which is def i ned as equation(11),will lead to determination of coeff i cient vector a(x).

In equation(11),gI(x)is the weight function of node I.Also,it is strictly positive(gI(x)>0)for all points located in the support domain of weight function.Moreover,xIis the Ithnode position,ˆuI(I=1,2,3,...,N∈Ωx)presents the f i ctitious nodal value.Furthermore,G,P andˆu are as follows:
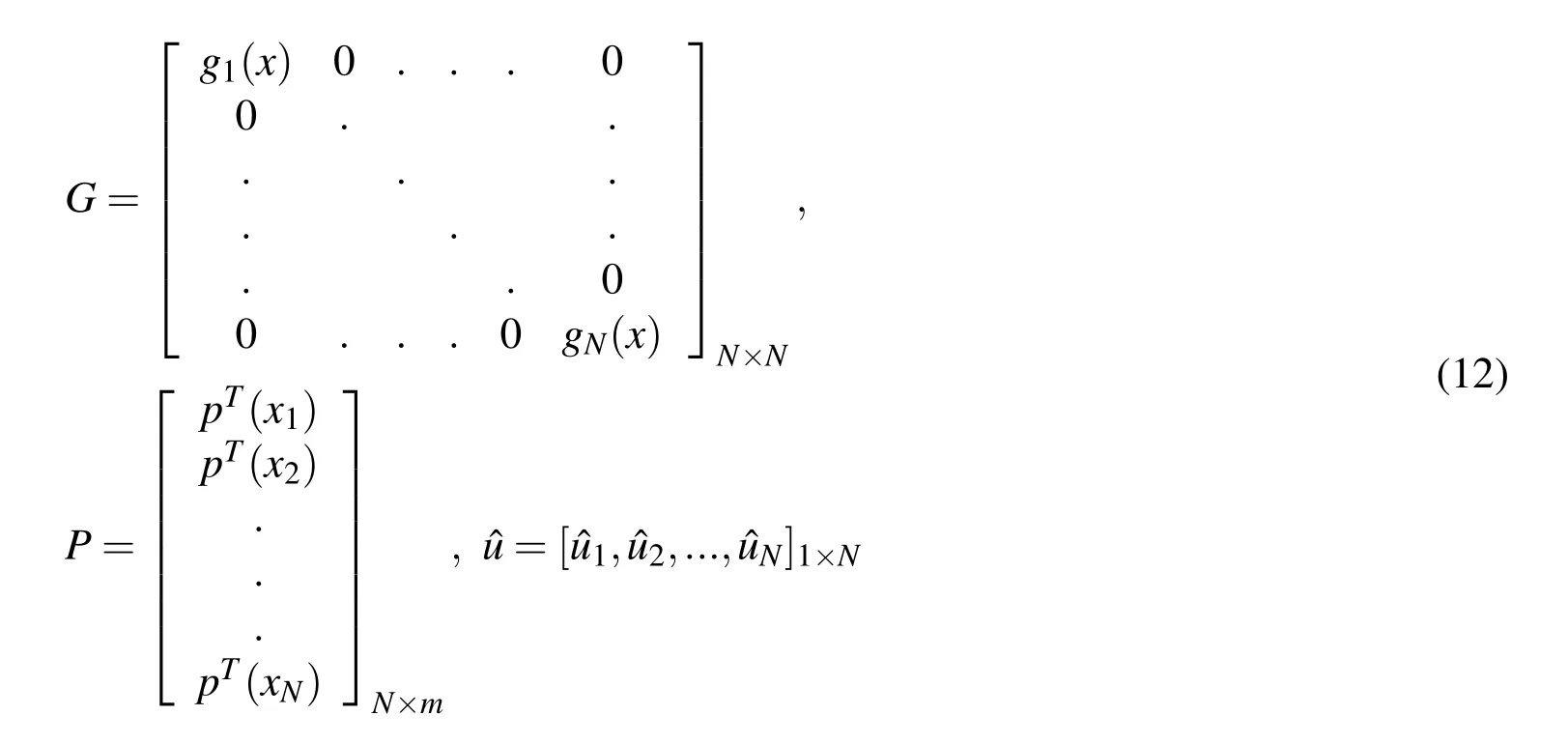
Then,a(x)is substituted in equation(9)and the approximation of u∗(ˆuI)can be obtained as:

In this equation ϕI(x)is the MLS approximation shape function and is def i ned as follows:

Also,equation(15)represents the partial derivatives of the trial function:

In this study ∂(.)/∂xiis denoted by(.),i.Meanwhile,derivatives of MLS shape function,is obtained as follows:

The dimensionless size of cubic support domain is denoted by γ.Also Riis the support size of the weight function,def i ned asThe average of nodal spacing in the vicinity of node I between two neighbor-ing nodes isd,where

3.3 Test function
In this study the test function assumed to be Heaviside step function which corresponds to MLPG5(Equation(18)).In MLPG5 method the local,nodal-based test function,over a local sub-domain centered at a node,is the Heaviside step function.By using this method there is no need for both a domain integral in the attendant symmetric weak-form and a singular integral.

Brick-shaped sub domain is selected for support of the test function.The subdomain dimension for node I is de fi ned as(2δd¯xI)×(2δd¯yI)×(2δd¯zI).In this expression,δ is a constant between 0 and 1.
3.4 Discretization of the weak form and numerical implementation
By substituting the MLS approximation function,Eq.(13),into Equation(8)and summing up for all nodes,the discretized system of linear equations is obtained as:

where˜S denotes the total number of nodes;˜K and˜M are the stiffness and mass matrixes,respectively.Therefore,for the MLPG5 method the following equations are obtained.
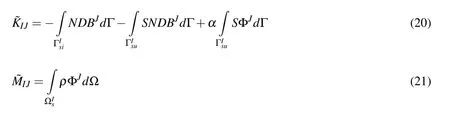
In 3D space,the vectors and matrices of equations(19)to(21),are as follows:
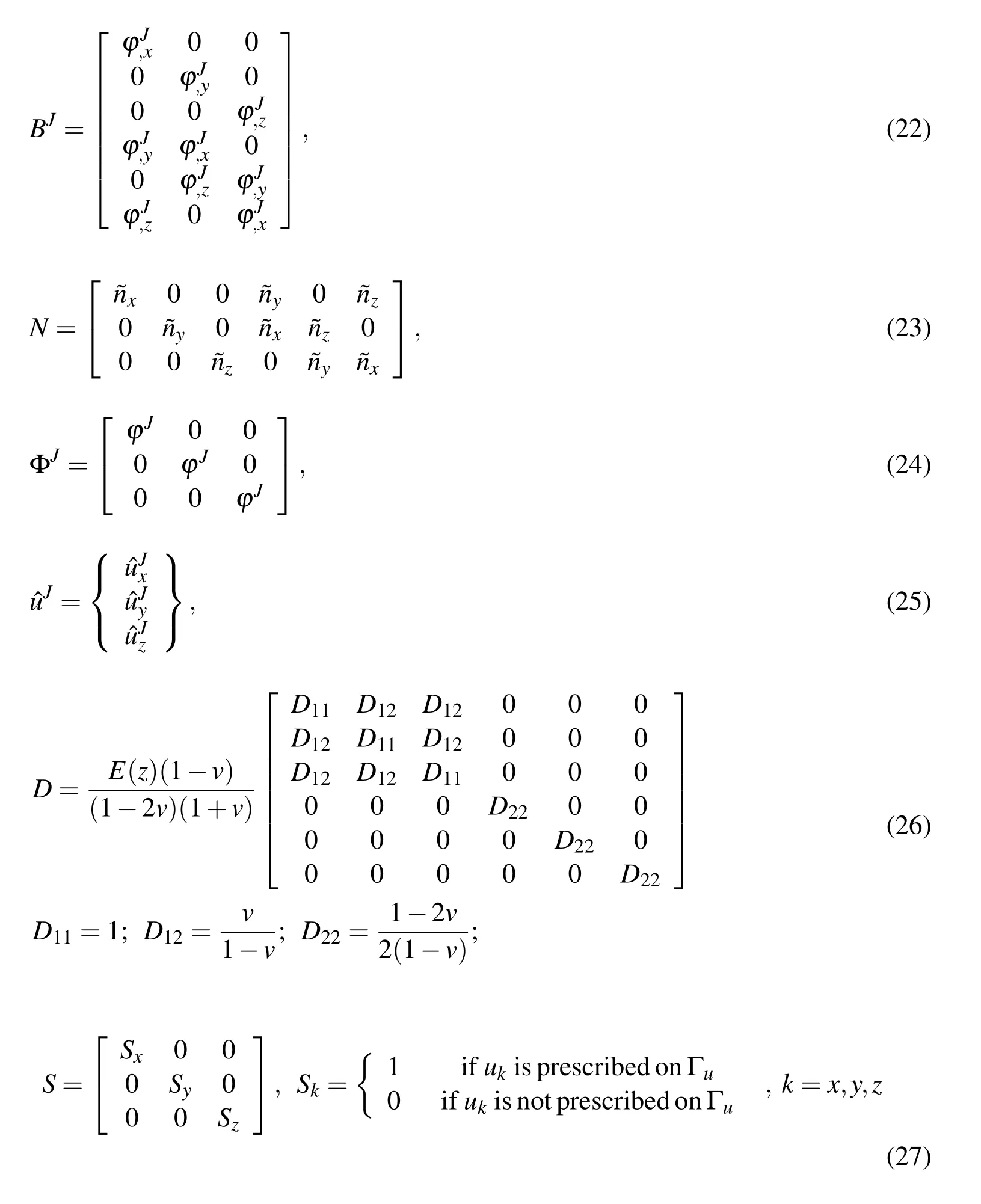
Also v and E are Poisson’s ratio and Young’s modulus,respectively.In this study the Young’s modulus and density of the structure are assumed to vary according to power-law model through the thickness.
4 Artif i cial Neural Network
Artif i cial Neural Networks are a paradigm for computing.They are based on a parallel architecture to human brains.These tools are a form of a multi-processor system with a high degree of inter-connection,simple processing elements,adoptive interaction between elements and simple scalar messages.The Multi-Layer Feed Forward(MLFF)is the most popular type of ANNs.A schematic diagram of a typical MLFF neural-network was used in this study is shown in Fig.4.The network consists of an input layer,some hidden layers and an output layer.In this network,knowledge is stored in connection weights.The process of modif i cation of the connection weights is called training.In this study,four ANNs are trained based on the Back-Error Propagation(BEP)method which is the most widely used learning algorithm of MLFF neural networks.The training method proposed by McClelland and Rumelhart(1986).For prediction of the f i rst four non-dimensional natural frequencies of FG plates,the inputs of the mentioned ANNs are FG core to plate thickness ratio and volume fraction index,and the target outputs are corresponding non-dimensional natural frequencies.In all ANNs,the transfer functions for the neurons of hidden and output layers are Tansig and is def i ned in equation(28).
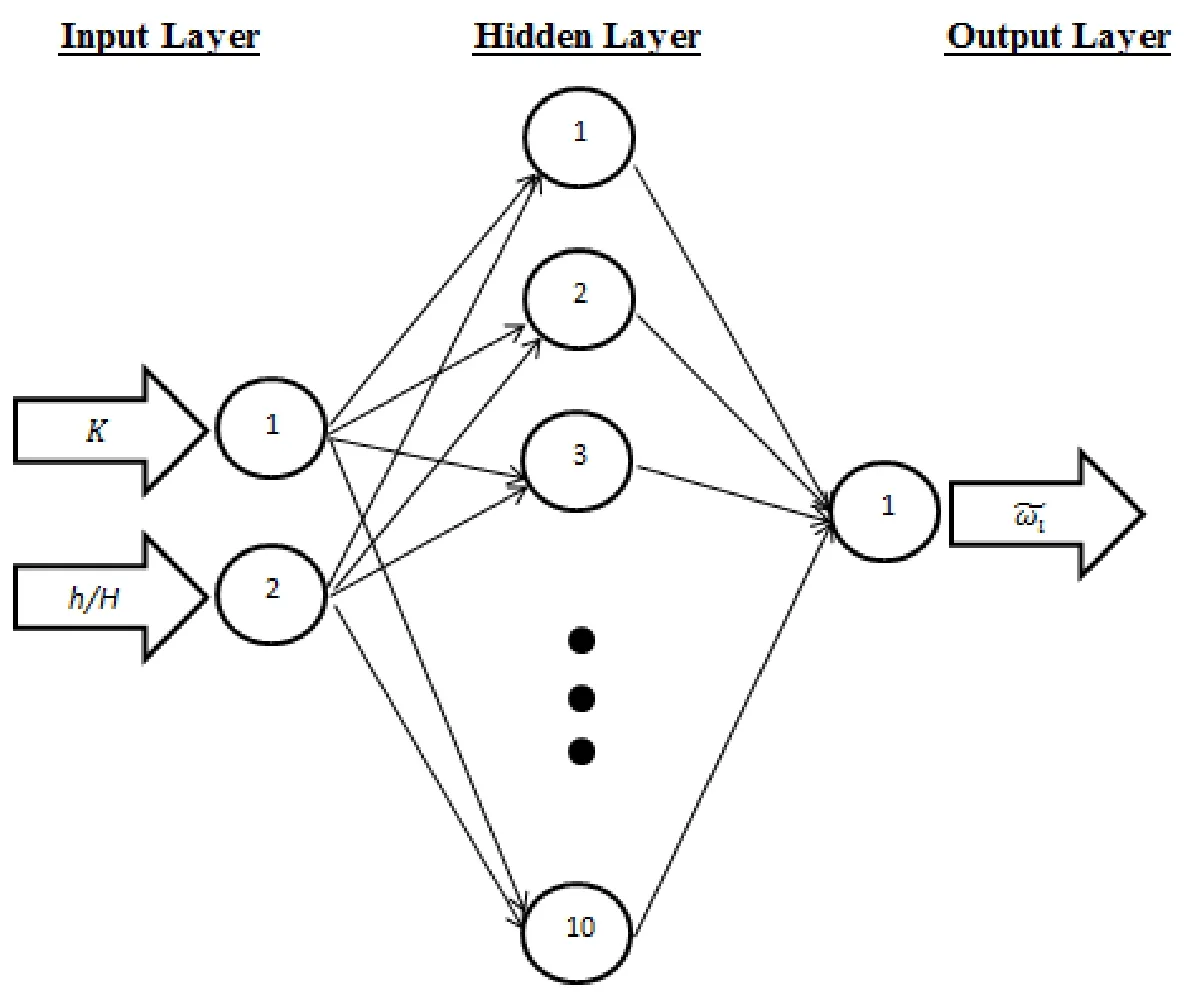
Figure 4:A schematic view of multi-layer feed forward neural network.

where the output of the neural network of f i gure 4,is ithnon-dimensional natural frequency of the plate(Equation(34)).
In this paper,the structure of the ANNs consists of three layers,i.e.the input,hidden and output layers.The operation of the BEP method consists of three steps as follows.
Feed-forward stage:

where O,T,Y and Φ are the output,input,output of hidden layer and activation function,respectively.
a)Back-propagation stage:

where Π is the local gradient function,µ shows the error function,O and D are the actual and desired outputs,respectively.
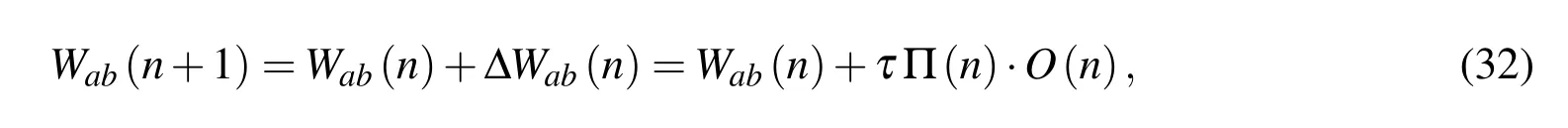
b)Adjustable weighted value stage:
The magnitudes of Waband Wbcare the weights between the input and hidden layers,and between the hidden and output layers,respectively.Also τ is the learning rate.
Repeating these 3 stages lead to a value of the error function,which will be zero or a constant value.
5 Results and discussion
The results are investigated for using MLPG itself as well as the hybrid MLPG and ANN.
5.1 MLPG results
In MLPG method,nodes are distributed in all three directions.The distance between nodes would be equal or unequal.To obtain the desired accuracy,the nodes can be added in each direction easily.Meanwhile,since the plate is investigated three dimensionally,each node has 3 degrees of freedom,i.e.,displacement in x,y and z directions which are denoted by ux,uyand uz,respectively.In the plate,the essential and natural boundary conditions are def i ned on the edges:0<x<a,0<y<a and 0<z<a.In this study,the assumed boundary condition is simply supported edges as:

In this study the dimensionless size of the sub-domain and support-domain are considered as δ =0.75 and γ=0.29.The values of these parameters are suggested from the assessment of the accuracy of results.Furthermore,216 gauss points are assumed in the local sub-domain integration.
5.1.1 Verif i cation
The MLPG solution procedure of this study is validated by comparing the natural frequencies of a simply supported square sandwich functionally graded plate with those presented by[Li,Iu and Kou(2008)].Same as[Li,Iu and Kou(2008)],The top layer in this study assumed to be Alumina with the Young’s modulus of 380GPa and the density of 3800kg/m3.Also,the Poisson’s ratio assumed to be constant and equal to 0.3.Meanwhile the bottom layer in this study assumed to be Aluminum with the Young’s modulus of 70GPa and the density of 2707kg/m3.
Theoretically,the Ritz method can provide the researchers with accurate and eff icient solutions.The natural frequencies determination in the Ritz approach starts with an initial value.These initial estimates are improved by increasing the number of terms of admissible functions in the computation[Li,Iu and Kou(2008)].Rather than many other numerical methods,the convergence rate in this method is very high and is independent of the volume fraction indices values[Li,Iu and Kou(2006)].
In Fig.5 the number of nodes in each x,y and z directions of the plate considered to be 9,10,11,12 or 13.In this study the natural frequency is presented in nondimensional form as:

where E0=1GPa and ρ0=1kg/m3.
Also the error is def i ned as equation(35)in percent.
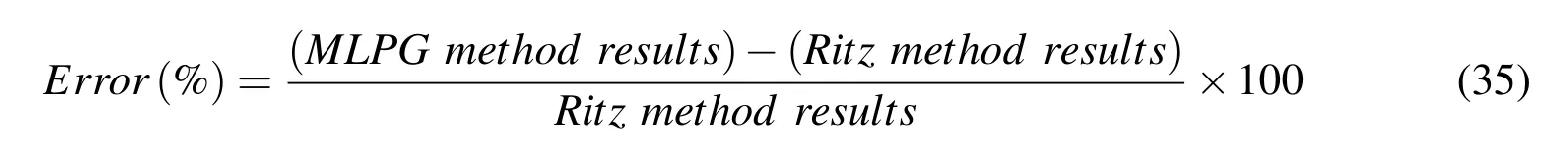
As can be seen in Fig.5 for 13 nodes in each direction,the error of f i rst,second and third natural frequencies are negligible where the error of forth natural frequency is about 2.6%.Therefore,13 nodes in each perpendicular Cartesian direction are selected for the subsequent analyses in this study.

Figure 5:Convergence study of MLPG Error of f i rst four non-dimensional natural frequencies for different node numbers in the sandwich FG plate.
5.1.2 Parametric analysis
According to the procedures and analyses of foregoing sections,a square sandwich plate with power-law FG core and four simply supported edges are investigated in this study.In this section,using the MLPG analysis,the effects of volume fraction index of power-law FG model and also FG core to plate thickness ratios on natural frequencies are discussed.
Fig.6shows the effect of volume fraction index on the f i rst four non-dimensional natural frequencies of the sandwich FG plate.These results are obtained for different values of FG core to plate thickness ratios.As can be seen in these graphs,from h/H=0.1 to h/H=0.4 all four natural frequencies versus κ value f l uctuate,and by increasing κ this f l uctuation is damped.Furthermore,from these graphs it is concluded that by increasing the h/H values from0.5 to 0.9,this f l uctuation decreases.Also it is resulted that h/H from 0.5 to 0.9,increasing the κ value from 3 to 10 has not meaningful in fl uence on the non-dimensional natural frequencies of the plate.The other point that can be found from Fig.6 is that the in fl uences of κ for all h/H values on all four natural frequencies are similar.Meanwhile,it can be concluded that from h/H=0.1 to h/H=0.3 the maximum value of natural frequencies belongs to κ =2,but for h/H=0.4 to h/H=0.9 it belongs to κ =1.Fig.7illustratestheeffectofFGcoretoplatethicknessratiosonthenon-dimensional fi rst four natural frequencies of the sandwich FG plate.These results are obtained for different values of volume fraction indexes.As can be seen,from κ=1 to 10 all four natural frequencies versus h/H values have some fl uctuations with a general increasing trend.Also it is concluded that the in fl uence of h/H for all κ values on all four natural frequencies are similar.Meanwhile,the point that was concluded from Fig.6 can be seen in Fig.7 more easily.As can be seen in Fig.7,from h/H=0.1 to 0.3,the natural frequencies values for κ=2 is higher than others but for h/H ≥0.4 the maximum value belongs to κ =1.Also from comparison of Fig.7 against Fig.6,no convergence to a constant value of natural frequency is seen in Fig.7.
5.2 Hybrid MLPG&ANN results
As stated before,in this study a combination of MLPG method and ANN is used to predict the natural frequencies of the sandwich FG plate.In this part of study,f i rst of all,four MLFF neural networks were created with one input,hidden and output layers,with 2,10 and 1 neurons,respectively.The inputs of the ithANNs is h/H and κ.The target output corresponds to ithnon-dimensional natural frequency of the plate.In the next step,the ANNs are trained based on the data of 72 different conditions of sandwich FG plate using the BEP method.In the training procedure of ANN,the BEP iterations are assumed to be 300.Taking another value for BEP iterations may affect the predicted results;but its investigation is not of concern in this study.The procedure of training using BEP is shown in Fig.8.In the BEP training procedure,70%,20%and 10%of data are used to train,test and verifying,respectively.As can be seen in Fig.8,the training error in BEP training process for all 4 cases is about or less than 10−3.MATLAB commercial software(2010)was employed for using ANN in this study.
5.2.1 Verif i cation
When ANN is trained by BEP,the trained ANNs are tested for 4 other conditions of the plate which have not been used in the training procedure.The obtained results are compared with MLPG results which are tabulated in Tab.1.It can be found from this table that the average error in prediction of 1st,2nd,3rdand 4thnon-dimensional natural frequencies of the sandwich plate using proposed hybrid MLPG&ANN method of this study are 1.36,2.16,1.64 and 0.45 percent,respectively.It can be also concluded that the predicted data have a good agreement with theactualdata.Therefore,theproposedmethodhasagoodcapabilityforprediction of natural frequencies of the sandwich FG plate.
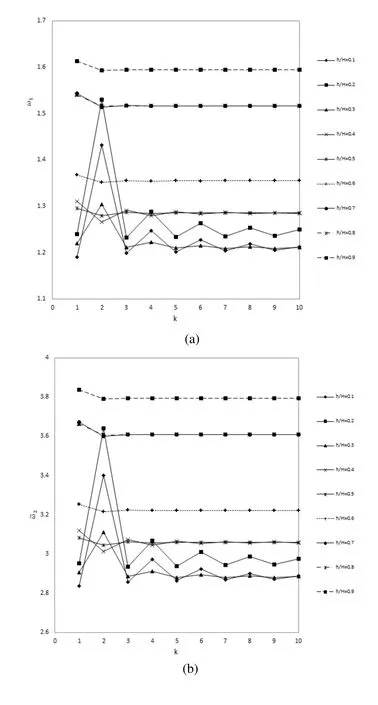

Figure 6:Effect of volume fraction index on the non-dimensional(a)1st(b)2nd(c)3rd&(d)4thnatural frequencies of the Sandwich FG Plate for different FG core to plate thickness ratios(MLPG Results).
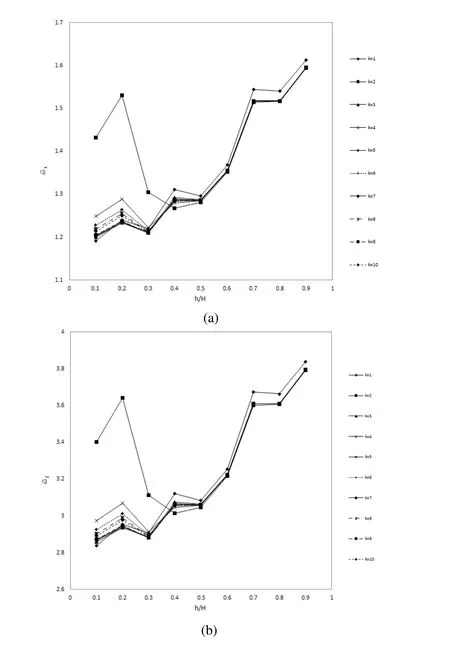

Figure 7:Effect of FG core to plate thickness ratios on the non-dimensional(a)1st(b)2nd(c)3rd&(d)4thnatural frequencies of the Sandwich FG Plate for different volume fraction indexes(MLPG Results).
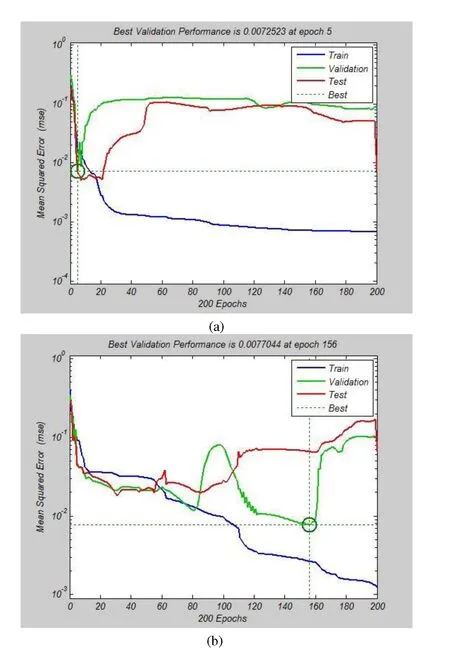

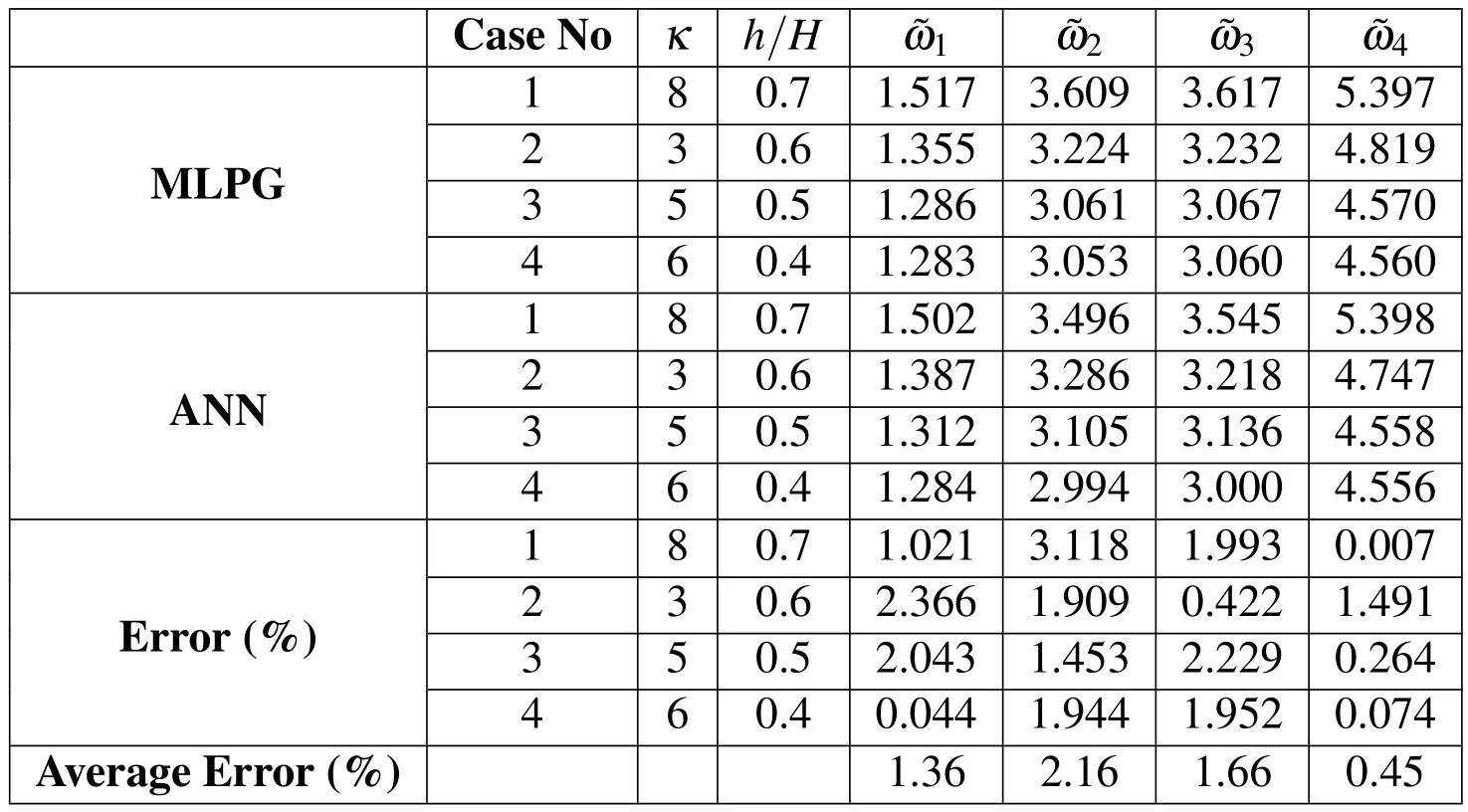
Table 1:Differences between actual and ANN predicted results for different values of K and h/H.
5.2.2 Prediction
In this section,using the trained ANNs f i rst four non-dimensional natural frequencies of the plate is obtained for some other volume fraction indexes and FG core to plate thickness ratios that MLPG results are not available.The Predicted results are tabulated in Tab.2.
6 Conclusion
This paper deals with 3D natural frequency analysis of a sandwich plate using hybrid MLPG and ANN methods.As a f i rst step,a convergence study for the f i rst four natural frequencies was performed using MLPG method.The obtained results were verif i ed with an available reference.Then a parametric study was performed on the MLPG results.In this part,the effects of two parameters:FG core to plate thickness ratio and volume fraction index on natural frequencies are investigated.
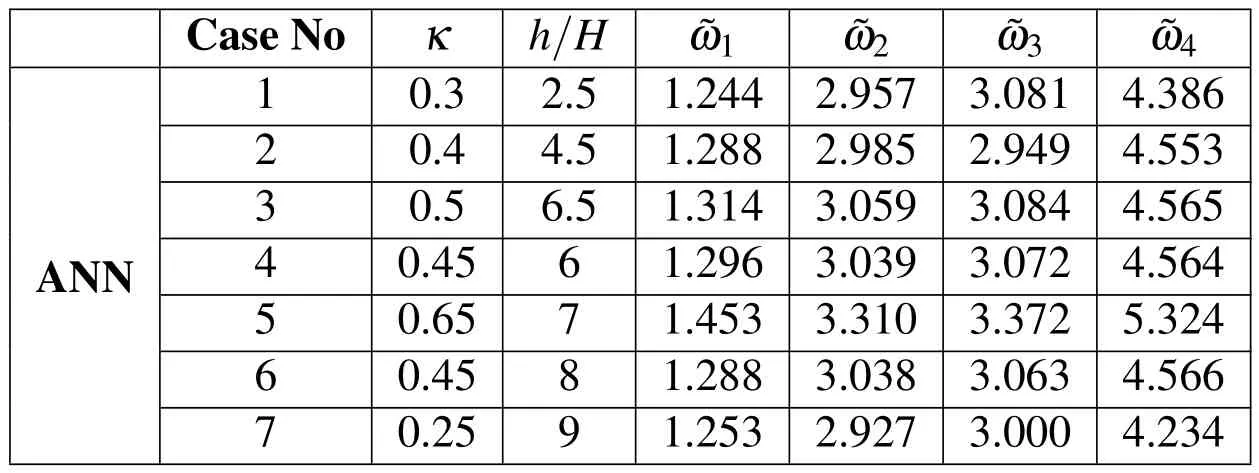
Table 2:Predicted ANN results for some conditions where MLPG results are not available.
From the parametric analysis of power-law index on the f i rst four natural frequencies,it was concluded that from h/H=0.1 to 0.4 all four natural frequencies versus κ values f l uctuate.Also by increasing κ,this f l uctuation is damped.Furthermore,by increasing the h/H values from 0.5 to 0.9,this f l uctuation decreases.Also it is found that for h/H from 0.5 to 0.9,increasing the κ value from 3 to 10,has not any signif i cant inf l uence on the natural frequencies of the plate.The other point is that the inf l uences of κ for all h/H values on all four natural frequencies are similar.
Also the parametric analysis of FG core to plate thickness ratios on the f i rst four natural frequencies of the plate reveals that for κ=1 to 10,all four natural frequencies versus h/H values have some f l uctuations with a general increasing trend.It was concluded that the inf l uences of h/H for all κ values on all four natural frequencies are similar.
Then the ANNs were used for prediction and analysis of the natural frequencies in some conditions which MLPG data are not available.
However,the main novelties of this study are as follows:
1)3D natural frequency analysis of a sandwich plate with FG core using MLPG method
2)Applying ANN to predict the natural frequencies
3)The effects of FG core to plate thickness ratio and volume fraction index on the natural frequencies of the plate are investigated
4)Specifying the optimum values of parameters that maximize the natural frequencies
All above novelties of this study can furnish a designer some benef i cial information on the natural frequencies of the sandwich plate with a FG core.
Atluri,S.N.;Shen,S.(2002):The Meshless Local Petrov–Galerkin(MLPG)Method.Tech.Science.Press.
Atluri,S.N.;Kim,H.G.;Cho,J.Y.(1999):A critical assessment of the truly meshless local Petrov–Galerkin(MLPG),and local boundary integral equation(LBIE)methods.Comput.Mech.,vol.24,pp.348–72.
Atluri,S.N.;Zhu,T.(2000):The meshless local Petrov–Galerkin(MLPG)approach for solving problems in elasto-statics.Comput.Mech.,vol.25,pp.169–79.
Atluri,S.N;Zhu,T.(1998):A new meshless local Petrov–Galerkin(MLPG)approach in computational mechanics.Comput.Mech.,vol.22,pp.117–27.
Avila,R.;Han,Z.;Atluri,S.N.(2011):A novel MLPG-f i nite-volume mixed method for analyzing Stokesian f l ows&study of a new vortex mixing f l ow.CMES:Comput.Model.Eng.Sci.,vol.71,no.4,pp.363-396.
Batra,R.C.;Jin.J.(2005):Naturalfrequenciesofafunctionallygradedanisotropic rectangular plate.J.Sound.Vib.,vol.282,pp.509–16.
Bishay,P.L.;Dong,L.;Atluri,S.N.(2014):Multi-physics computational grains(MPCGs)for direct numerical simulation(DNS)of piezoelectric composite/porous materials and structures.Comput.Mech.,vol.54,no.5,pp.1129-1139.
Cheng,Z.Q.;Batra,R.C.(2000):Exact correspondence between eigenvalues of membranes and functionally graded simply supported polygonal plates.J.Sound.Vib.,vol.229,pp.879–95.
Dong,L.;Atluri,S.N.(2011):A simple procedure to develop eff i cient&stable hybrid/mixed elements,and Voronoi cell f i nite elements for macro-µmechanics.CMC:Comp.Mat.Cont.,vol.24,no.1,pp.61.
Dong,L.;Atluri,S.N.(2012):A Simple Multi-Source-Point Trefftz Method for Solving Direct/Inverse SHM Problems of Plane Elasticity in Arbitrary Multiply-Connected Domains.CMES:Comput.Model.Eng.Sci.,vol.83,no.1,pp.1-43.
Dong,L.;Atluri,S.N.(2012):T-Trefftz Voronoi cell f i nite elements with elastic/rigid inclusions or voids for micromechanical analysis of composite and porous materials.CMES:Comput.Model.Eng.Sci.,vol.83,no.2,pp.183-219.
Dong,L.;El-Gizawy,A.S.;Juhany,K.A.;Atluri,S.N.(2014):A simple locking-alleviated 4-node mixed-collocation f i nite element with over-integration,forhomogeneousorfunctionally-gradedorthick-sectionlaminatedcompositebeams.CMC:Comp.Mat.Cont.,vol.40,no.1,pp.49-77.
Dong,L.;El-Gizawy,A.S.;Juhany,K.A.;Atluri,S.N.(2014):A Simple Locking-Alleviated 3D 8-Node Mixed-Collocation C0 Finite Element with Over-Integration,forFunctionally-GradedandLaminatedThick-SectionPlatesandShells,with&without Z-Pins.CMC:Comp.Mat.Cont.,vol.41,no.3,pp.163-192.
Dozio,L.(2013):Natural frequencies of sandwich plates with FGM core via variable-kinematic 2-D Ritz models.Compos.Struct.,vol.96,pp.561-568.
Ferreira,A.J.M.;Batra,R.C.;Roque,C.M.C.;Qian,L.F.;Jorge,R.M.N.(2006):Natural frequencies of functionally graded plates by a meshless method.Compos.Struct.,vol.75,pp.593–600.
Ghouhestani,S.;Shahabian,F.;Hosseini,S.M.(2014):Dynamic Analysis of a Layered Cylinder Reinforced by Functionally Graded Carbon Nanotubes Distributions Subjected to Shock Loading using MLPG Method.CMES:Comput.Model.Eng.Sci.,vol.100,no.4,pp.295-321.
Gilhooley,D.F.;Batra,R.C.;Xiao,J.R.;McCarthy,M.A.;Gillespie,J.W.(2007):Analysis of thick functionally graded plates by using higher-order shear and normal deformable plate theory and MLPG method with radial basis functions.Compos.Struct.,vol.80,pp.539–52.
Godinho,L.;Dias-da-Costa,D.;Behera,D.;Chakraverty,S.;Knupp,D.C.;Silva Neto,A.J.;Yi,M.;Huang,J.;Wang,L.(2013):The MLPG(5)for the analysisoftransientheattransferinthefrequencydomain.CMES:Comput.Model.Eng.Sci.,vol.96,no.5,pp.293-316.
Hosseini,S.M.(2014):Application of a hybrid meshless technique for natural frequencies analysis in functionally graded thick hollow cylinder subjected to suddenly thermal loading.Appl.Math.Model.,vol.38,pp.425-436.
Hosseini,S.M.;Abolbashari,M.H.(2010):General analytical solution for elastic radial wave propagation and dynamic analysis of functionally graded thick hollow cylinders subjected to impact loading.Acta.Mech.,vol.212.no.1-2,pp.1-19.
Hosseini,S.M.;Shahabian,F.;Sladek,J.;Sladek,V.(2011):Stochastic Meshless Local Petrov-Galerkin(MLPG)Method for Thermo-Elastic Wave Propagation Analysis in Functionally Graded Thick Hollow Cylinders.CMES:Comput.Model.Eng.Sci.,vol.71,no.1,pp.39-66.
Iqbal,Z.;Muhammad,N.N.;Nazra,S.(2009):VibrationcharacteristicsofFGM
circular cylindrical shells using wave propagation approach.Acta.Mech.,vol.208,no.3-4,pp.237-248.
Jodaei,A.;Jalal,M.;Yas,M.H.(2012):Free vibration analysis of functionally graded annular plates by state-space based differential quadrature method and comparative modeling by ANN.Compos.Part B.,vol.43,pp.340-353.
Jodaei,A.;Jalal,M.;Yas,M.H.(2013):Three-dimensional free vibration analysis of functionally graded piezoelectric annular plates via SSDQM and comparative modeling by ANN.Math Comp Model.,vol.57,pp.1408-1425.
Kamarian,S.;Yas,M.H.;Pourasghar,A.(2013):VolumeFractionOptimization of Four-Parameter FGM Beams Resting on Elastic Foundation.Int.J.Adv.Des.Manuf.Tech.,vol.64,pp.75-82.
Li,Q.;Iu,V.P.;Kou,K.P.(2006):Three-dimensional vibration analysis of functionallygraded materialrectangular plates byChebyshev polynomials,Proceedings of the Tenth International Conference on Enhancement and Promotion of Computational Methods in Engineering and Science,Sanya,China.
Li,Q.;Iu,V.P.;Kou,K.P.(2008):Three-dimensional vibration analysis of functionally graded material sandwich plates.J.Sound.Vib,vol.311,pp.498–515.
Liu,K.Y.;Long,S.Y.;Li,G,Y.(2008):A meshless local Petrov-Galerkin method for the analysis of cracks in the isotropic functionally graded material.CMC:Comp.Mat.Cont.,vol.7,no.1,pp.43.
Loy,C.T.;Lam,K.Y.;Reddy,J.N.(1999):Vibration of functionally graded cylindrical shells.Int.J.Mech.Sci.,vol.41,pp.309–24.
MATLAB and Neural Network Toolbox.(2010):The Math Works,Inc.,Natick,Massachusetts,United States.
Matsunaga,H.(2008):Free vibration and stability of functionally graded plates according to a 2-D higher-order deformation theory.Compos.Struct.,vol.82,pp.499–512.
Moussavinezhad,S.M.;Shahabian,F.;Hosseini,S.M.(2013):Two-dimensional elastic wave propagation analysis in f i nite length FG thick hollow cylinders with 2D nonlinear grading patterns using MLPG method.CMES:Comput.Model.Eng.Sci.,vol.91,no.3,pp.177-204.
Neves,A.M.A.;Ferreira,A.J.M.;Carrera,E.;Cinefra,M.;Roque,C.M.C;Jorge,R.M.N.;Soares C.M.M.(2013):Static,free vibration and buckling analysis of isotropic and sandwich functionally graded plates using a quasi-3D higher-order shear deformation theory and a meshless technique.Compos.Part B,vol.44,pp.657-674.
Praveen,G.N.;Reddy,J.N.(1998):Nonlinear transient thermo-elastic analysis of functionally graded ceramic–metal plates.Int.J.Solids.Struct.,vol.35,pp.4457–76.
Qiana,L.F.;Batra,R.C.;Chena,L.M.(2004):Staticanddynamicdeformations of thick functionally graded elastic plates by using higher-order shear and normal deformable plate theory and meshless local Petrov–Galerkin method.Compos:Part B.,vol.35,pp.685–97.
Rezaei Mojdehi,A.;Darvizeh,A.;Basti,A.;Rajabi,H.(2011):Three dimensional static and dynamic analysis of thick functionally graded plates by the meshless local Petrov–Galerkin(MLPG)method.Eng.Anal.Bound.Elem.,vol.35,pp.1168–80.
Roque,C.M.C.;Ferreira,A.J.M.;Jorge,R.M.N.(2007):A radial basis function approach for the free vibration analysis of functionally graded plates using a ref i ned theory.J.Sound.Vib.,vol.300,pp.1048–70.
Rumelhart,D.E.;McClelland,J,L.(1986):Parallel distributed processing.Explorations in the microstructure of cognition,vol.1-2.
Sladek,J.;Sladek,V.;Krivacek,J.;Zhang,C.H.(2005):MeshlesslocalPetrov-Galerkin method for stress and crack analysis in 3-D axisymmetric FGM bodies.CMES:Comput.Model.Eng.Sci.,vol.8,no.3 pp.259-270.
Sladek,J.;Sladek,V.;Solek,P.;Tan,C.L.;Zhang,C.H.(2009):Two-and three-dimensional transient thermoelastic analysis by the MLPG method.CMES:Comput.Model.Eng.Sci.,vol.47,no.1,pp.61.
Sladek,j.;Sladek,V.;Solek,V.(2009):Elastic analyses in 3D anisotropic functionally graded solids by the MLPG.CMES:Comput.Model.Eng.Sci.,vol.43,pp.223-251.
Sladek,J.;Sladek,V.;Tan,C.L.;Atluri,S.N.(2008):Analysis of transient heat conduction in 3D anisotropic functionally graded solids,by the MLPG method.CMES:Comput.Model.Eng.Sci.,vol.32,no.3,pp.161-174.
Sladek,J.;Sladek,V.;Zhang,C.H.;Solek,P.;Starek,L.(2007):Fracture analyses in continuously nonhomogeneous piezoelectric solids by the MLPG.CMES:Comput.Model.Eng.Sci.,vol.19,no.3,pp.247.
Sladek,J.;Stanak,P.;Han,Z.D.;Sladek,V.;Atluri,S.N.(2013):Applications of the MLPG method in engineering&Sciences:A review.CMES:Comput.Model.Eng.Sci.,vol.92,pp.423-475.
Sladek.J.;Sladek,V.;Zhang,C.H.(2005):Stress analysis in anisotropic functionally graded materials by the MLPG method.Eng.Anal.Bound.Elem.,vol.29,pp.597–609.
Vel,S.S.;Batra,R.C.(2004):Three-dimensional exact solution for the vibration of functionally graded rectangular plates.J.Sound.Vib.,vol.272,pp.703–30.
Zenkour,A.M.A.(2005):comprehensive analysis of functionally graded sandwich plates:Part 2–buckling and free vibration.Int.J.Solids.Struct.,vol.42,pp.5243–58.
Zhang,T.;Dong,L.;Alotaibi,A.;Atluri,S.N.(2013):Application of the MLPG mixedcollocationmethodforsolvinginverseproblemsoflinearisotropic/anisotropic elasticity with simply/multiply-connected domains.CMES:Comput.Model.Eng.Sci.,vol.94,no.1,pp.1-28.
Zhang,T.;He,Y.;Dong,L.;Li,S.;Alotaibi,A.;Atluri,S.N.(2014):Meshless local Petrov-Galerkin mixed collocation method for solving Cauchy inverse problems of steady-state heat transfer.CMES:Comput.Model.Eng.Sci.,vol.97,no.6,pp.509-553.
1Mechanical Engineering Department,Lean Production Engineering Research Center,Ferdowsi University of Mashhad,PO Box 91775-1111,Mashhad,Iran.
2Corresponding author.Tel:+98-51-38805004;Fax:+98-51-38763304;E-mail:abolbash@um.ac.ir
3Industrial Engineering Department,Faculty of Engineering,Ferdowsi University of Mashhad,PO Box 91775-1111,Mashhad,Iran.
