基于Bézier曲线的两平行线间缓和曲线构造

蔡华辉， 柳炳祥， 程 燕

（1. 景德镇陶瓷学院信息工程学院，江西 景德镇 333403；2. 景德镇陶瓷学院设计艺术学院，江西 景德镇 333403）

基于Bézier曲线的两平行线间缓和曲线构造

蔡华辉1， 柳炳祥1， 程 燕2

（1. 景德镇陶瓷学院信息工程学院，江西 景德镇 333403；2. 景德镇陶瓷学院设计艺术学院，江西 景德镇 333403）

利用五次Bézier曲线，构造了一条含形状参数的两平行线间满足G2连续的缓和曲线。这条曲线在 t=1/2含有唯一的曲率极值点。利用形状参数可以方便地控制曲率极值的大小和调节曲线的形状。

缓和曲线；5次Bézier曲线；平行线；曲率单调

构造两直线、直线和圆弧、两圆弧之间光滑拼接的缓和（过渡）曲线在道路设计，车型机器人的轨道模拟和曲线的光顺设计等工程应用中都是一个基本问题。通常要求缓和曲线在与直线或圆弧相接触点处满足 G2连续，且在曲线内部曲率极值点尽可能少，一般要求两直线间的缓和曲线内部只含有一个曲率极值点，直线和圆弧利用一条曲率单调曲线缓和，两圆弧间缓和曲线最多含一个曲率极值点。由于螺线弧是曲率恒正或恒负，且曲率单调变化的曲线[1]，因此常用于缓和曲线的设计。回旋曲线因其曲率和弧长成正比的特性，在道路设计中用于缓和曲线的设计[2]。近年来，利用the generalized Cornu spiral[3]、log-aesthetic curves[4]、Fermat's spiral[5]等设计缓和曲线。

由于许多常用的螺线是利用超越函数定义，不能被有限项多项式或有理多项式表出。因此，许多学者提出利用多项式曲线来设计缓和曲线。在计算机辅助几何设计(computer aided geometric design, CAGD)领域内，利用参数多项式曲线设计缓和曲线的研究最早可以追溯到Walton和Meek[6-7]的工作，在文献[6-7]中分别提出了起点曲率为 0的三次Bézier螺线弧和五次PH螺线弧，然后分别利用这两条螺线弧替代回旋曲线作为道路设计中的缓和曲线，取得了良好效果。在文献[6-7]中，两直线间或两圆弧间的缓和曲线都由两条螺线弧拼接而成。Walton和Meek[8-9]对文献[6-7]的结果进行了推广，增加了曲线的自由度。Ahmad等[10-11]提出了一条四次Bézier螺线弧，并应用与两非平行线间的缓和曲线设计。Habib和Sakai[12-13]讨论了如何利用一条三次Bézier曲线和五次PH曲线设计两圆间的缓和曲线。但一直以来，如何利用Bézier曲线设计两平行线间缓和曲线的方法一直没有给出。

1 基于三次Bézier螺线的平行线间缓和曲线

构造两平行线间缓和曲线最直接的方法是利用已知直线和圆弧间缓和曲线的构造方法和图形对称性来构造。Walton和 Meek[6]给出了一条起点曲率为0的三次Bézier螺线弧。

引理. 给定一条以P0, P1, P2, P3为控制顶点的三次Bézier曲线P(t)，设其首末端点的单位切向量分别为T0, T1，终点处的曲率为κα, T0到T1的有向转角为θ，且0 ＜θ ＜π/2, 控制顶点P1, P2, P3满足：

则这条Bézier曲线满足：

显然，只要给定起点P0的2个坐标、起点单位切向量T0、T0到终点单位切向量T1转角θ以及终点处曲率κα，就可以确定这条三次Bézier螺线弧。利用文献中构造直线和圆弧间缓和曲线的结论，容易推得基于三次Bézier螺线的两平行线间缓和曲线的构造方法。

定理1. 如图1所示，直线L1和L2是间距为d的两条平行线，N为直线单位法向量且方向由 L1指向L2，T是直线的单位方向向量且T与N构成右手系，设P0和Q0分别是直线L1和L2上互为投影的两点，则在平行线L1和L2之间通过P0和Q0的缓和曲线可由以P0, P1, P2, P3为控制顶点的三次Bézier螺线P(t)，以Q0, Q1, Q2, Q3为控制顶点的三次Bézier螺线Q(t)和以r半径的圆弧拼接而成，其中半径曲线P(t)的控制顶点满足：

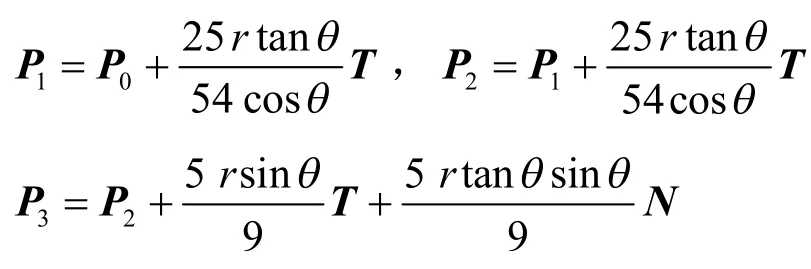
其中，θ满足：

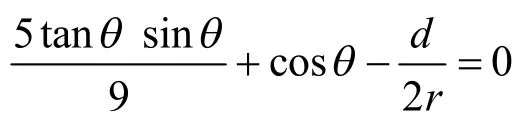
圆弧的圆心C满足：

曲线Q(t)的控制顶点满足：

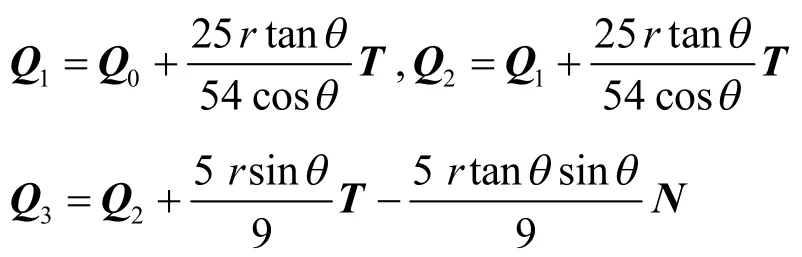
可以看到，此时的缓和曲线是由三条曲线拼接而成，结果比较麻烦。因此，需要寻求利用一条曲线构造缓和曲线的方法。

图1 基于三次Bézier螺线的两平行线间缓和曲线

2 基于五次Bézier曲线的平行线间缓和曲线

要利用一条Bézier曲线设计两平行线间的缓和曲线，由Bézier曲线性质知道，Bézier曲线必须满足起始3个控制顶点共线和最后3个控制顶点也共线，因此，Bézier曲线的最低次数是五次。下面构造出一条五次Bézier曲线：

使P（t ）在0＜t＜1内只含有一个曲率极值点，因此可作为两平行线间的缓和曲线。

如图2所示，设直线L1和L2是间距为d的两条平行线，取L1与y轴平行，P0与原点重合，取P5(d,0), P1, P2, P3, P4满足：

则式(1)为：

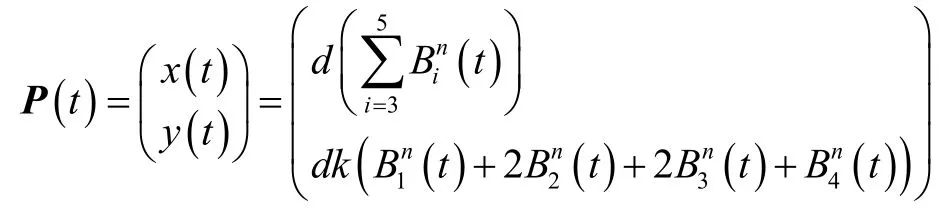
对上式求一阶和二阶导数：

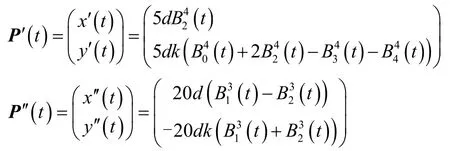
则利用上面两式，曲线曲率为：

再对 κ（t ）求导为：

式中：

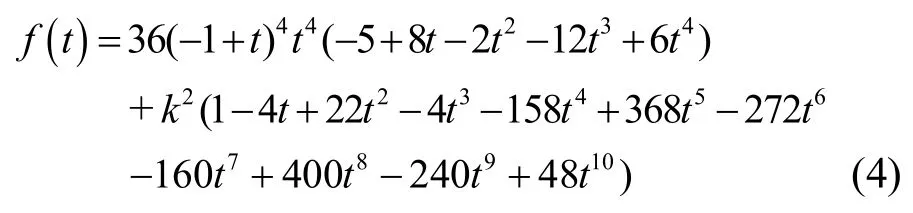
由式(3)可知，t=1/2时，曲率κ（t ）取极值为：

为了证明P（t）在0＜t＜1内只含有一个曲率极值点，还需要证明f（t）在0＜t＜1内正负恒不变。

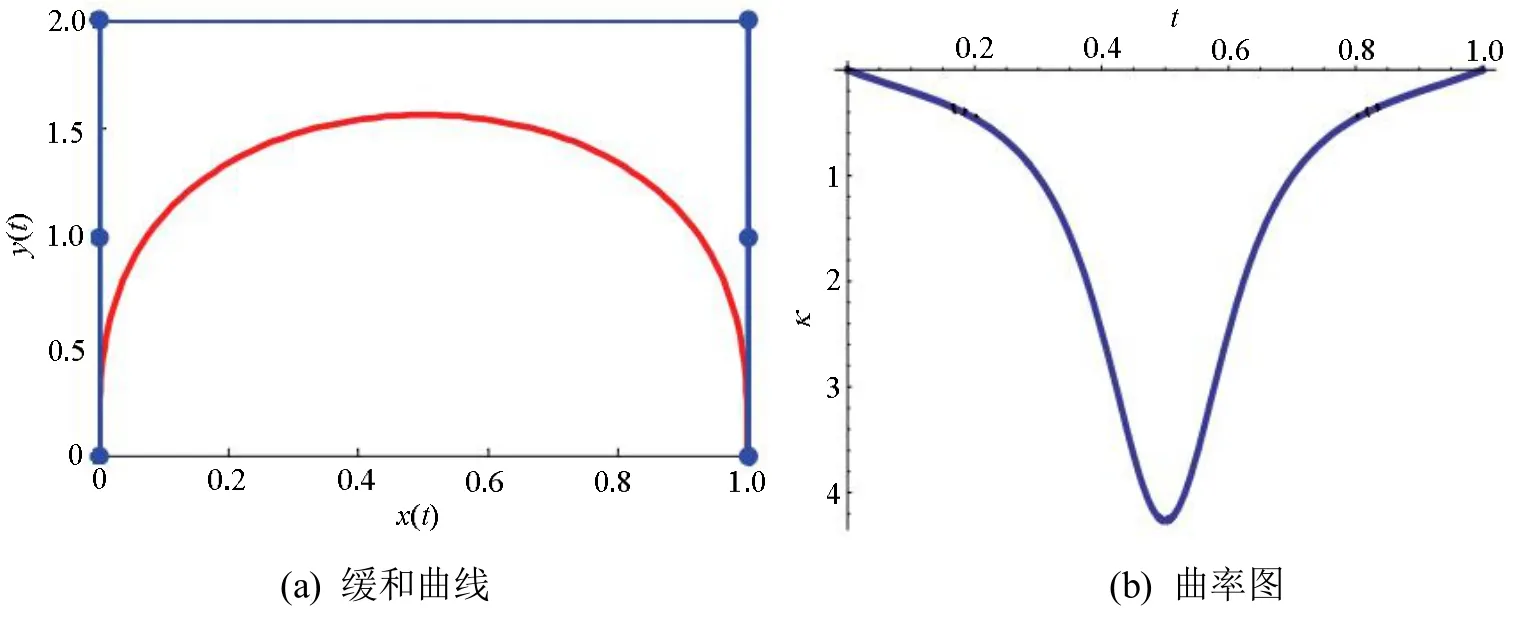
图2 五次Bézier缓和曲线

定理 2. 当参数k满足k2≥2767时，式(4) f（t）在0＜t＜1内恒大于零。

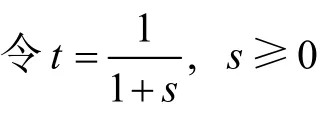
则式(4)f（t）转换为：

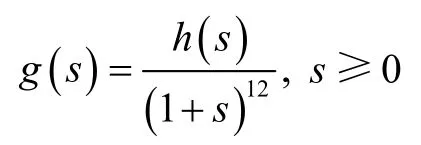
式中：

系数ia分别是：

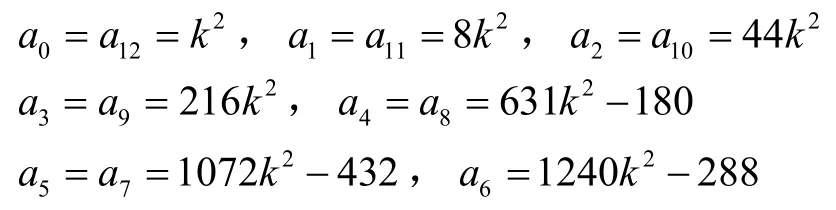
由上式，若：

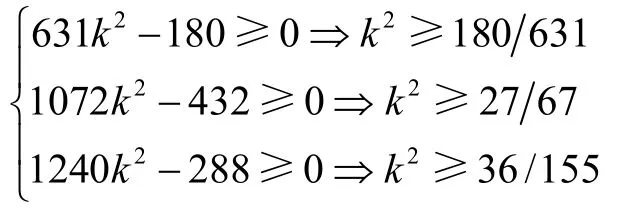
满足， h(s)在区间(0,+∞) 恒大于零，即定理 2得证，又因为：

因此定理2成立。 证毕。

当k2＜2767时候，κ′(t)在(0,1)内极值点个数情况如下：

(1) 当 k2≤36155时，h(s)系数的正负号依次为：

即 h(s)系数的正负号变号数为 2，由 the Descartes rule of signs[14]和h（s）=0的正根个数为2或0可得，在h(0)＜0,h(+∞)→+∞时，h（s）=0有两个正根，即κ′（t ）在（0,1）内有3个极值点。

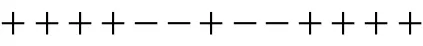
尽管上面构造的五次Bézier曲线要求P0取原点，直线方向为y轴方向，但由Bézier曲线的几何不变性，即曲线形状在坐标系平移和旋转后不变。

定理3. 设直线L1和L2是间距为d的两条平行线，N为直线单位法向量且方向由L1指向L2，T是直线的单位方向向量且N与T构成右手系，设P0为L1上任意一点，给定任意满足k2≥2767的形状参数k，令：

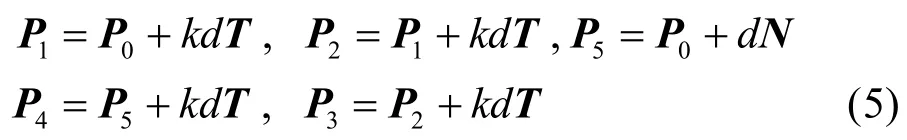
则以P0, P1, P2, P3, P4, P5为控制顶点的Bézier曲线P（t）满足：

曲线P（t ）的曲率κ（t ）满足：

且κ（t ）在t=1/2取0＜t＜1内唯一极值点：

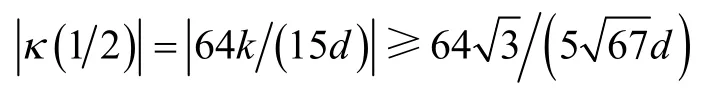
在缓和曲线设计中，曲线曲率极值由定理 3可以求得，且形状参数可以控制曲线的极值，因此，根据实际设计问题，可以选取合适的参数k值。

3 结 束 语

本文利用 Bézier曲线讨论了两条平行线间缓和曲线的构造方法。首先利用三次 Bézier螺线弧设计了缓和曲线，由于此时缓和曲线是利用三段曲线拼接而成，线型较复杂。然后利用五次Bézier曲线设计构造了两平行线间缓和曲线。此时缓和曲线只有一条含形状参数的 Bézier曲线，同时能利用形状参数调节曲率极值和曲线形状。但是在道路设计中，五次 Bézier曲线的最后一个控制顶点P5由于障碍等原因不一定能满足式(5)，在实际应用中只需要P5在直线L2上即可，此时如何构造缓和曲线是今后值得探讨的问题。

[1] Guggenheimer H W. Differential geometry [M]. New York: Dover Publications, 1977: 48-53.

[2] Baass K G. The use of clothoid templates in highway design [J]. Transportation Forum, 1984, 1: 47-52.

[3] Ali J M, Tookey R M, Ball J V, et al. The generalised Cornu spiral and its application to span generation [J]. Journal of Computational and Applied Mathematics, 1999, 102(1): 37-47.

[4] Ziatdinov R, Yoshida N, Kim T. Fitting G2multispiral transition curve joining two straight lines [J]. Computer-Aided Design, 2012, 44(6): 591-596.

[5] Lekkas A M, Dahl A R, Breivik M, et al. Continuous-curvature path generation using Fermat's spiral [J]. Modeling, Identification and Control, 2013, 34(4): 183-198.

[6] Walton D J, Meek D S. A planar cubic Bézier spiral [J]. Journal of Computational and Applied Mathematics, 1996, 72(1): 85-100.

[7] Walton D J, Meek D S. A Pythagorean hodograph quintic spiral [J]. Computer Aided Design, 1996, 28(12): 943-950.

[8] Walton D J, Meek D S. A further generalisation of the planar cubic Bézier spiral [J]. Journal of Computational and Applied Mathematics, 2012, 236(11): 2869-2882.

[9] Walton D J, Meek D S. Curve design with more general planar Pythagorean-hodograph quintic spiral segments [J]. Computer Aided Geometric Design, 2013, 30(7): 707-721.

[10] Ahmad A, Gobithasan R, Ali J M. G2transition curve using quartic Bézier curve [C]//Proceedings of the 4th International Conference on Computer Graphics, Imaging and Visualization, Bangkok, Thailand, 2007: 223-228.

[11] Ahmad A, Ali J M. G3transition curve between two straight lines [C]//Proceedings of the 5th International Conference on Computer Graphics, Imaging and Visualization, Penang, Malaysia, 2008: 154-159.

[12] Habib Z, Sakai M. G2cubic transition between two circles with shape control [J]. Journal of Computational and Applied Mathematics, 2009, 223(1): 133-144.

[13] Habib Z, Sakai M. G2Pythagorean hodograph quintic transition between two circles with shape control [J]. Computer Aided Geometric Design, 2007, 24(5): 252-266.

[14] Polya G, Szego G. Problems and theorems in analysis II: theory of functions, zeros, polynomials, determinants, number theory, geometry [M]. New York, Springer, 2004: 36-51.

Transition Curve between Parallel Lines Based on Bézier Curve

Cai Huahui1, Liu Bingxiang1, Cheng Yan2

(1. School of Information Engineering, Jingdezhen Ceramic Institute, Jingdezhen Jiangxi 333403, China; 2. School of Art & Design, Jingdezhen Ceramic Institute, Jingdezhen Jiangxi 333403, China)

By using quintic Bézier curve, the transition curve which is G2continuous with a shape parameter is constructed between two parallel lines. This curve at t=1/2 contains a unique curvature extreme. It can be easily controlled curvature extremes and adjust the shape of the curve by using the shape parameter.

transition curve; quintic Bézier curve; parallel lines; monotone curvature

TP 391

A

2095-302X(2015)03-0363-04

2014-10-08；定稿日期：2014-10-24

国家自然科学基金资助项目(61262038, 61164014)；江西省自然基金资助项目(2012BAB201044)；景德镇市科技局资助项目

蔡华辉(1975-)，男，浙江东阳人，副教授，博士。主要研究方向为计算机辅助几何设计与计算机图形学。E-mail：huahuicai@gmail.com