一类双参数三次Bézier曲线的形状分析
2015-12-19刘植,李晨,谢进,费腾
刘 植, 李 晨, 谢 进, 费 腾
(1. 合肥工业大学数学学院,安徽 合肥 230009;2. 合肥学院科学计算研究所,安徽 合肥 230601)
一类双参数三次Bézier曲线的形状分析
刘 植1, 李 晨1, 谢 进2, 费 腾1
(1. 合肥工业大学数学学院,安徽 合肥 230009;2. 合肥学院科学计算研究所,安徽 合肥 230601)
为了分析清楚形状参数对一类双参数三次Bézier曲线形态的影响及实现其对该曲线形状的调控,利用包络理论与拓扑映射的方法对一类双参数三次Bézier曲线进行了形状分析,明确了形状参数对曲线的影响,画出了曲线的形状特征分布图,得出了曲线上有奇点、拐点和曲线为局部凸或全局凸的充分必要条件,这些条件完全由控制多边形的相对位置表示,并进一步讨论了形状参数对曲线形状的影响。
Bézier曲线;奇点;拐点;曲线形状;形状参数
Bézier曲线[1-3]以Bernstein多项式作为基函数,具有许多优良的性质,受到了工业界和计算机辅助几何设计(computer aided geometric design, CAGD)学术界的广泛重视。1972年,Forrest发现处理作为Bézier曲线多边形的相对矢量不如处理作为顶点的绝对矢量方便,而且上述Bézier基表示形式能被等价地改写成使用控制顶点定义的Bernstein基表示形式。但是,由一组给定的控制顶点生成的Bézier曲线曲面的形式是固定的,形状的局部修改非常困难。有理Bézier方法中的权因子可以用于调控曲线曲面的形状[4],但权因子的选取及求导、求积分运算比较复杂。为了更加灵活、简便地调控曲线曲面的形状,通过引入形状参数对Bézier方法进行扩展,得到形状可调的参数多项式曲线曲面[5-6]。
三次Bézier曲线扩展有许多形式,文献[7]提出了一种简单重要的扩展形式。参数三次Bézier曲线具有许多便于曲线设计的几何性质,如端点性质、对称性、凸包性、变差减小性、几何不变性,且可以通过改变形状参数的取值,达到整体或者局部调控曲线形状的目的。双参数三次Bézier曲线有着更强的形状调控能力,随着参数λ,μ的增大更加地逼近控制多边形,反之则远离控制多边形。对于给定的控制多边形,通过引入形状参数,改变形状参数取值来整体或局部调控曲线的形状,为CAGD曲线曲面的设计带来了很大的便利。
在平面三次参数曲线的分类和形状控制问题上,苏步青和刘鼎元[8]通过引进几何不变量的方法,彻底解决了该问题,对CAGD作出了重要贡献。曲线的奇点、拐点、尖点及凸性分布对于确定曲线的形状至关重要[9-11]。形状参数的引入使曲线形状特征分布图更加简单且易于判断。而本文利用包络理论与拓扑映射的方法对双参数三次Bézier曲线进行形状分析,明确了形状参数对曲线的影响,得出了曲线上有奇点,拐点和曲线为局部凸或全局凸的充分必要条件。
1 双参数三次Bézier曲线
定义. 给定4个控制顶点Pi∈Rd(d=2,3; i=0,1,2,3),对∀t∈[0,1],定义曲线:

为双参数三次Bézier曲线。其中,基函数Bi(t)为:

其中,λ,μ为形状参数,且λ,μ∈(-2,1]。当λ=1,μ= 1时,双参数三次Bézier曲线就是三次Bézier曲线。
由式(1)定义的双参数三次Bézier曲线含有2个独立的形状参数,具有与三次Bézier曲线类似的几何性质,且扩展后的曲线与Bézier曲线次数一致,对于给定的控制顶点,可以通过改变形状参数的取值对曲线的形状做整体或局部调整。
2 空间双参数三次Bézier曲线的形状分析
定理1. 若控制顶点Pi∈R3(i=0,1,2,3)不共面,则当λ,μ∈(-2,1]时,双参数三次Bézier曲线P(t)无奇点(尖点,二重点)和泛拐点,且曲线与控制多边形的旋转方向一致。
证明. 设qi=Pi-Pi-1(i=1,2,3)为控制多边形的边向量,将P(t)改写为:
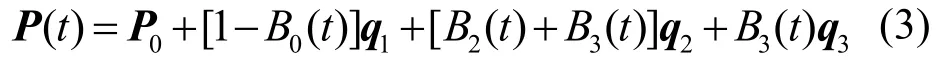
求导得:

由式(2)可知,当(0,1)t∈时,

又控制顶点Pi∈R3(i=0,1,2,3)不在同一个平面上,也就是说边向量qi(i=1,2,3)线性无关,所以P′(t)≠0,即P(t)不可能有尖点。
再者,若曲线P(t)有二重点,设有0≤t1<t2≤1,得:

代入式(3)得:

因为边向量qi(i=1,2,3)线性无关,故:

令B0′(t)=0解得t=1(舍去),由:

解得λ>1或λ<-2,与λ∈(-2,1]矛盾,即B0′(t)≠0,从而B0(t)为单调函数,不可能有B0(t1)=B0(t2),故曲线P(t)无二重结点。
空间曲线上挠率变号的点称为泛拐点。令g(t)=det(P′(t),P′(t),P′′(t )),注意到:

则:

其中,(q1,q2,q3)为边向量q1,q2,q3的混合积,由于q1,q2,q3不共面,则(q1,q2,q3)≠0;D(t)=12(2+λ)(2+μ),由于参数λ,μ满足:λ,μ∈(-2,1],故D(t)>0。
对任意0≤t≤1,有g(t)≠0且与(q1,q2,q3)同号,因此曲线P(t)没有泛拐点。又D(t)>0,故曲线P(t)与其控制多边形的旋转方向相同。
3 平面双参数三次Bézier曲线的形状分析
若双参数三次Bézier曲线的4个控制顶点共面(不妨设Pi∈R2,i=0,1,2,3),则P(t)为平面曲线,此时(q1,q2,q3)=0,边向量qi(i=1,2,3)线性相关。以下根据 q1与 q3是否平行分别进行讨论。
3.1 q1不平行q3的情形
当 q1不平行 q3时,以 q1,q3为平面的基向量,令q2=uq1+vq3,代入式(3)得:

若P′(t)=0(0<t <1),即:
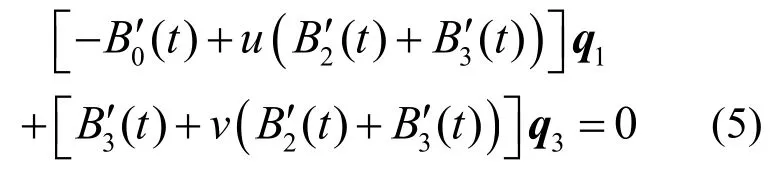
由于1q与3q线性无关,则有:

代入基函数并化简得:

下面讨论曲线C的形态,由式(6)易知:

故曲线C有两条渐近线:

考察单调性和凹凸性,由式(6)可知:

即曲线C为单调下降曲线(-2<λ,μ≤1,0<t <1),又:

即曲线C无拐点,曲线C如图1所示。
下面将基于上述单调递减,且严格凸的曲线C,进一步讨论曲线P(t)的尖点、拐点、重结点和凸性情况。
3.1.1 关于尖点
曲线P(t)有尖点的必要条件是P′(t)=0(0<t <1),任取一点(u0,v0)∈C,与该点对应的参数值设为t0(0<t0<1),此时P′(t0)=0。
又P(t)在 t0处的Taylor展开式为:

求导得:

其中,P′′(t0)≠0。事实上,对式(5)再求一次导,有:

由于1q与3q线性无关,则有:

即:

联立式(6)和式(7)可得λ=μ=-2,与λ,μ∈(-2,1]矛盾,因此P′(t0)≠0。
由P′(t0)=0,P′(t0)≠0可知,P′(t)经过t0时方向反变,所以P(t0)是尖点(见参考文献[12])。
结论. 曲线P(t)上有尖点等价于(u,v)∈C。3.1.2 关于拐点
点P(t0)(0<t0<1)是曲线P(t)的拐点当且仅当P′(t)×P′′(t)经过 t0时符号发生改变,经式(4)计算得:

其中:

因此,P(t0)(0<t0<1)是曲线P(t)的拐点当且仅当f(t;u,v)经过 t0时符号发生改变。而在uv平面,使得曲线P(t)有拐点的可能区域必为直线族f(t;u,v)=0所覆盖,由包络理论与拓扑映射的方法可知(文献[12]),此直线族的包络为:

即:

解方程即得式(6),可以说明直线族的包络正好是曲线C。
讨论曲线C的形态可知,曲线C是严格凸的连续曲线,因此曲线 C的切线所扫过的区域为S∪D∪C,此即为拐点区域。如图1所示,其中D区域是由两条渐近线:

和曲线C所围部分(不含C);S区域由两部分构成,一部分是两条渐近线相交的左上部分,另一部分是两条渐近线相交的右下部分。图1(a)中形状参数λ=-1,μ=0;图1(b)中λ=1,μ=1;图1(c)中λ=0,μ=-1。
由图 1可知,双参数三次 Bézier曲线比三次Bézier曲线的单拐点区域更大,但是双拐点区域则更小。
过任一点(u0,v0)∈S∪D∪C 至少有一条uv平面上的直线f(t0;u,v)=0与曲线C相切。当(u0,v0)∈C时,设对应的参数为 t0,由Taylor展开式得:

其中:

又λ,μ∈(-2,1],t0∈(0,1),容易得到ftt′(t0;u0,v0)≠0,所以f(t;u0,v0)经过t0时不变号,即曲线P(t)无拐点。
当(u0,v0)∈S∪D时,设过它且与曲线C相切的直线为f(t0;u,v)=0,其中,t0为切点对应的参数,则由Taylor展开式得:

其中,ft′(t0;u0,v0)≠0(因为若ft′(t0;u0,v0)=0,则由包络定义可知(u0,v0)∈C),从而f(t;u0,v0)经过t0时变号,即P(t0)是曲线P(t)的拐点。
结论. 若(u0,v0)∈S,过此点只能作曲线C的一条切线,对应曲线P(t)只有一个拐点;若(u0,v0)∈D,过此点只能作曲线 C的两条切线,对应曲线P(t)只有2个拐点。

图1 尖点拐点区域分布
3.1.3 关于重结点
曲线P(t)有重结点当且仅当存在0≤t1<t2≤1,使得P(t1)-P(t2)=0,由式(4)可知,等价于u,v,t1,t2满足方程组:
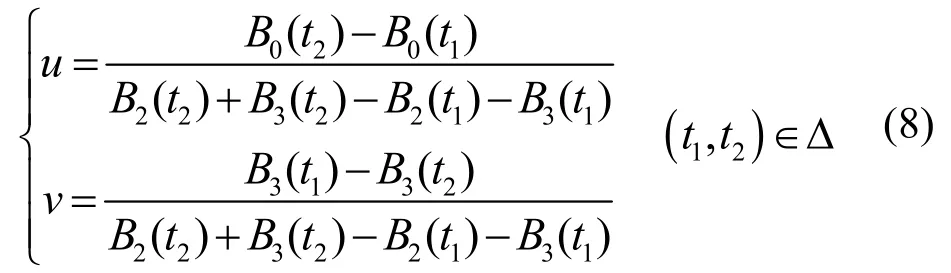
容易验证,式(8)定义了一个拓扑映射:

因此,象域L=F(Δ)是uv平面上单连通区域,Δ的3条边界线:t1=t2,t1=0,t2=1分别对应于L的3条边界线:曲线C(不属于L)、L1和L2(都属于L),其中:

当-2<λ,μ≤1,0<t<1时,对于曲线L1,易知:
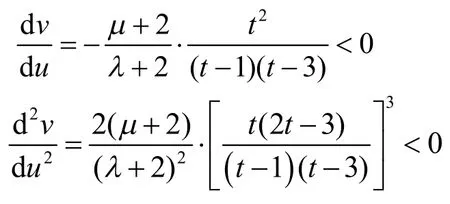
对于曲线L2,类似的有:

因此,曲线L1和L2均为单调下降,严格凸的连续曲线,且曲线L1以为渐近线,曲线L2以为渐近线。曲线L1和L2相交于点(-1,-1)。
结论. 由曲线C(不属于L),L1和L2(都属于L)围成的单连通区域L中的点(u0,v0)对应的曲线P(t)有且仅有一个二重结点。
3.1.4 关于凸性
记N=R2(C∪S∪D∪L),曲线 L1,L2(不包括边界 L1,L2)所围成的左上部分区域为N1,右下部分区域为N2,N0=N(N1∪N2),如图2所示。
由前面讨论易知,当(u,v)∈N时,曲线P(t)无尖点、重结点和拐点。记向量:
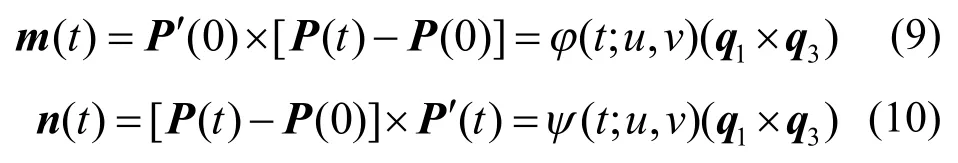
由式(4)和式(5)直接计算可得:
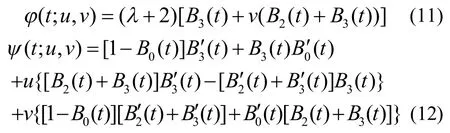
对于任意的 t0∈(0,1),如果由式(9)和式(10)所确定的向量和向量P′(t)×P′′(t)=f(t;u,v)(q1×q3)经过 t0时符号不发生改变,则曲线P(t)为全局凸;如果向量P′(t)×P′′(t)=f(t;u,v)(q1×q3)经过t0时符号不发生改变,而向量m(t)=φ(t;u,v)(q1×q3)或者向量n(t)=ψ(t;u,v)(q1×q3)经过t0时符号发生改变,则曲线P(t)为局部凸[10]。
由3.1.2节的讨论可知,当(u,v)∈N=N0∪N1∪N2时f(t;u,v)不变号,所以向量P′(t)×P′′(t)=f(t;u,v) (q1×q3)经过t0时方向不发生反变。式由(11)可知当时,向量m(t)=φ(t;u,v)(q1×q3)经过与v相对应的参数t时方向反变,容易算出 v的取值范围是所以当(u,v)∈N1时,曲线P (t)为局部凸。事实上还可以证明:1N恰好是2L的切线所覆盖区域在N中部分。
解关于 ,uv的方程:

求得的直线族ψ(t;u,v)=0的包络恰好是直线L1, L1的切线在 N中所扫过的区域为N2,当(u,v)∈N2时,曲线P(t)为局部凸。
由3.1节的讨论可得,平面参数三次Bézier曲线的形状分布图,如图 2所示。其中,图 2(b)是三次 Bézier曲线的形状分布图,且当形状参数λ=μ时,曲线P(t)的形状分布图关于直线u=v对称。
结论. 当(u,v)∈N0时,P′(t)×P′′(t),m(t), n(t)都不变号,曲线P(t)为全局凸[11];当(u,v)∈N1时,P′(t)×P′′(t),n(t)不变号,m(t)有一处变号,曲线P(t)为局部凸;当(u,v)∈N2时,P′(t)×P′′(t),m(t)不变号,n(t)有一处变号,因此曲线P(t)为局部凸[11]。
定理2. 当q1不平行q3时,设q2=uq1+vq3,平面双参数三次 Bézier曲线P(t)的形状特征取决于点(u,v)在uv平面的分布,如表1所示。

图2 平面参数三次Bézier曲线的形状分布图

表1 平面双参数三次Bézier曲线的形状特征分布
3.2 q1平行q3的情形
当q1//q3时,以q1,q2为平面的基向量,设q3=αq1,代入式(3)有:

3.2.1 关于尖点
类似3.1.1节的讨论,曲线P(t)有尖点等价于P′(t)=0,t ∈(0,1),由式(13)得:

由于q1,q2线性无关,由P′(t)=0可得:

易知式(14)无解,故平面双参数三次Bézier曲线P(t)无尖点。
3.2.2 关于拐点
类似3.1.2的讨论可知,点P(t0)(0<t0<1)是曲线P(t)的拐点当且仅当P′(t)×P′′(t )经过t0时符号发生改变,经式(13)计算得:

其中:
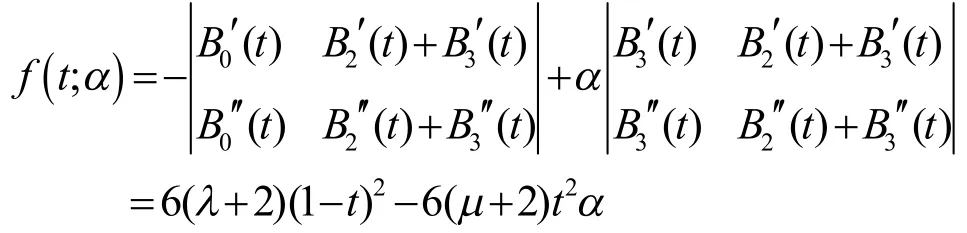
因此,P(t0)(0<t0<1)是曲线P(t)的拐点当且仅当f(t;α)经过 t0时符号发生改变。又当α>0时,

即(;)ftα在(0,1)t∈内关于t是单调递减函数。而且,

所以有唯一的t0使得f(t;α ) 经过 t0时符号发生改变。因此当且仅当α>0,即 q1,q3方向相同(不包括4点共线)时,平面双参数三次Bézier曲线P(t)有且只有一个拐点。
3.2.3 关于重结点
曲线P(t)有重结点当且仅当存在0≤t1<t2≤1,使得P(t1)-P(t2)=0,由式(13)可知,P(t1)-P(t2)=0等价于α,t1,t2满足方程组:

即:

由于(3t2-2t3)′=6t(1-t )>0,所以式(15)无解,即平面双参数三次Bézier曲线P(t)无二重点。
定理3. 当 q1//q3时:
(1) 平面双参数三次Bézier曲线P(t)无尖点、二重点;
(2) 当且仅当α>0,即 q1,q3方向相同(不包括4点共线)时,曲线P(t)有且只有一个拐点。
4 形状参数对曲线形态的影响及其对曲线形状的调控
由定理2,进一步讨论形状参数,λμ对平面双参数三次Bézier曲线形状有以下影响,如图3所示。
(1) 固定参数λ后,曲线 L1随着参数μ的增大而逐渐靠近u轴,区域S,N0逐渐减小,区域D,N1∪N2逐渐增大。固定参数μ时,曲线 L2随着参数λ的增大而逐渐靠近v轴,区域S,N0逐渐减小,区域D,N1∪N2逐渐增大。因此,通过调节形状参数λ, μ可以灵活的调节曲线的形状,这为几何设计中的光滑拼接带来了更加灵活的自由度。
(2) 当(u,v)∈{(u,v)|-1≤u,v <0}{(-1,-1)},即控制多边形首末两条边相交(首末端点重合除外)时,曲线P(t)上可能出现奇点、单拐点或者双拐点,也可能是全局凸,但不可能是局部凸,调节形状参数能使P(t)成为全局凸曲线。
(3) 随着形状参数λ,μ的增大,曲线C被朝原点(0,0)方向拉伸,曲线 L1被朝点(-1,0)方向拉伸,曲线 L2被朝点(0,-1)方向拉伸。因此,区域S,N0逐渐减小,区域D,N1∪N2,L逐渐增大。
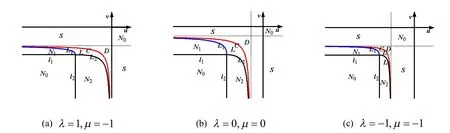
图3 参数对曲线形态分布的影响
[1] 郭清伟, 胡 梅. 以给定的三次 Bézier曲线为边界测地线的双三次 Bézier曲面构造[J]. 图学学报, 2014, 35(4): 523-527.
[2] Han Liwen, Chu Ying, Qiu Zhiyu. Generalized Bézier curves and surfaces based on Lupas q-analogue of Bernstein operator [J]. Journal of Computational and Applied Mathematics, 2014, 261: 352-363.
[3] Zhou Lian, Wei Yongwei, Yao Yufeng. Optimal multi-degree reduction of Bézier curves with geometric constraints [J].Computer Aided Design, 2014, 49: 18-27.
[4] 韩力文, 楚 瑛, 李 丁, 等, 基于 Lupas q-模拟Bernstein 算子的广义Bézier曲线[J]. 图学学报, 2013, 34(4): 63-68.
[5] Qin Xinqiang, Hu Gang, Zhang Nianjuan, et al. A novel extension to the polynomial basis functions describing Bézier curves and surfaces of degreen with multiple shape parameters [J]. Applied Mathematics and Computation, 2013, 223: 1-16.
[6] Han Xian, Huang Xili, Ma Yichen. Shape analysis of cubic trigonometric Bézier curves with a shape parameter [J]. Applied Mathematics and Computation, 2010, 217(6): 2527-2533.
[7] 刘 植, 陈晓彦, 张 莉, 等. Bézier曲线曲面的同次扩展[J]. 中国科技论文在线, 2011, 6(10): 721-725.
[8] 苏步青, 刘鼎元. 计算几何[J]. 数学进展, 1981, 10(1): 35-47.
[9] 吴荣军, 彭国华, 罗卫民. 一类带参 B样条曲线的形状分析[J]. 计算数学, 2010, 32(4): 349-360.
[10] 吴晓勤, 韩旭里.四次带参Ball曲线的形状分析[J]. 应用数学学报, 2011, 34(4): 671-682.
[11] 陈福来, 吴晓勤, 朱秀云. 广义三次DP曲线的形状分析[J]. 电子设计工程, 2012, 20(12): 5-8, 12.
[12] 叶正麟, 魏生民, 冯国胜. 张力平面参数曲线的几何性态[J]. 西北工业大学学报, 1995, 13(3): 458-463.
Shape Analysis of a Class of Cubic Bézier Curve with Two Shape Parameters
Liu Zhi1, Li Chen1, Xie Jin2, Fei Teng1
(1. School of Mathematics, Hefei University of Technology, Hefei Anhui 230009, China; 2. Institute of Scientific Computing, Hefei University, Hefei Anhui 230601, China)
The shape features of a class of Bézier curve with two shape parameters are analyzed by using the method based on the theory of envelope and topological mapping. Investigate effects of the shape parameter on the curve shape. Necessary and sufficient conditions are derived for this curve having one or two inflection points, a loop or a cusp, or be locally or globally convex. Those conditions are completely characterized by the relative position of the edge vectors of the control polygon. Furthermore we discussed the influences of shape parameter on the shape diagram and the ability for adjusting the shape of the curve.
Bézier curve; singular points; inflection points; curve shape; shape parameter
TP 301
A
2095-302X(2015)03-0356-07
2014-10-08;定稿日期:2014-10-24
国家自然科学基金资助项目(61070227,11471093);高等学校博士学科点专项科研基金资助项目(20110111120026);安徽省高等学校自然科学研究资助项目(KJ2014ZD30);中央高校基本科研业务费专项经费资助项目(2012HGXJ0039)
刘 植(1976-),男,安徽金寨人,副教授,博士。主要研究方向为计算机辅助几何设计、计算机图形学。E-mail:liuzhi314@126.com
