卡尔曼滤波在变形监测中的应用

金廷文

（中交三航局第二工程有限公司，上海 200122）

0 引言

卡尔曼滤波器是一个“最优化自回归数据处理算法”，它是在线性最小方差估计的基础上的数学结构比较简单的最优线性递推滤波方法。卡尔曼滤波的实质是由量测值重构系统的状态向量，它以“预测—实测—修正”的顺序递推，根据系统的量测值来消除随机干扰，再现系统的状态，或根据系统的量测值从被污染的系统中恢复系统的本来面目[1-2]。

从以上分析可以看出卡尔曼滤波就是在有随机干扰和噪声的情况下，以线性最小方差估计方法给出状态的最优估计值，卡尔曼滤波是在统计的意义上给出最接近状态真值的估计值。因此，在变形监测中，卡尔曼滤波可以利用新的变形监测观测值，通过不断地预测和修正即可估计出系统新的状态值，这正适用于处理多期重复观测的监测网的观测数据，从而对监测网进行形变分析。

1 卡尔曼滤波的模型

卡尔曼滤波模型由状态方程（1）和观测方程（2）组成[3]，基本的数学模型如下[1]：

式中：Xk为k时刻系统状态向量；φk，k-1为k-1时刻到k时刻的系统状态转移矩阵；Γk，k-1为k-1时刻到k时刻系统状态噪声输入矩阵；Ωk为输入噪声；Wk为观测值的噪声序列；Zk为k时刻系统观测向量；Hk为k时刻系统的观测矩阵，Δk为k时刻系统观测噪声。

通过该数学模型就可以进行状态估值Xk的求解了。

2 变形监测滤波模型的建立

2.1 状态方程

变形监测是一种动态测量，物体的变形就是物体的空间位置随时间的改变，也就是在一定时间内发生的位移。传统的数据处理方法是从静态的角度对各期数据观测值进行单独平差，然后对各期的变形量加以比较，这样就反映了监测点在相应时间内的变形情况。而为了更好地了解被研究物体的变形状态，仅仅求得一定时间内的变形量是不够的，还应知道监测点在某时刻的沉降速度甚至加速度，从而可以预测其未来的趋势。

设有一组变形监测点，其位移过程是一个随机过程。在tk时刻的位置用xk表示，形变速度用vk表示，运动加速度用ak表示，动态噪声用Ωk表示。对这些状态参数常用的运动模型是将监测点的位置和形变速度及形变加速度都视作状态参数，而将形变加速度的变化率视作动态噪声，运动方程为公式（3）：

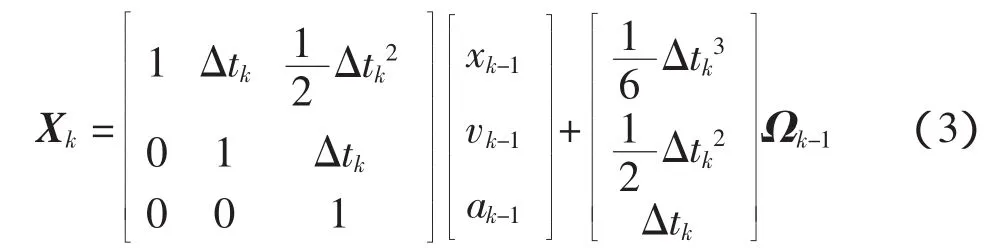
Ωk为三维形变加速度的动态噪声矩阵，Δtk为tk时刻和tk-1时刻的时间差。

对应到状态方程（1）中，可得

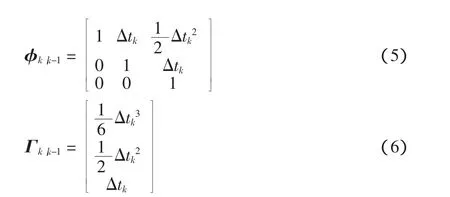
2.2 观测方程

变形监测中通常观测的是监测点的变形情况，即监测点在tk时刻和tk-1时刻位置，由两个时刻的空间位置得到的位移向量即为形变量，其观测方程与方程（2）相同。

以上公式为一维动态监测网（沉降监测）适用公式，如果是二维平面监测网或三维空间监测网，需要根据不同的观测值确定模型中的Xk和Zk的维数，建立正确的滤波模型。

3 实例分析

本算例以港珠澳大桥东人工岛暗埋段沉降监测数据为原始数据，暗埋段地基通过降水、堆载预压处理后，打设PHC桩，并在PHC桩顶部铺设碎石垫层及浇筑混凝土垫层。

为了监测暗埋段的沉降情况，每节段暗埋段共布设4个监测点，位于4个角点处，观测得到的数据为沉降量的时间特征，在进行数据处理前，要进行数据的初级处理，将沉降量的时间特征化算到累积沉降量的时间特征。选取其中一个点（点号CE3-1-N2）的观测数据作为处理实例，各期观测值沉降量见表1。

表1 点CE3-1-N2沉降监测数据Table 1 The settlement data of point CE3-1-N2

结合运动方程及观测方程，Zk为一维的累积沉降量观测值，则Hk= [1 0 0]，由于速度值是状态参数，而速度的初始值需要前两期的数据共同来确定，则从第三期开始进行滤波处理。数据初始值X0的协方差阵及观测噪声的协方差阵，根据变形监测的精度要求及测量规范，按照变形监测等级给定初始值X0的方差为0.5 mm2，权逆阵为单位阵，则初始值的协方差阵为：

滤波过程分两步进行，第1步是对前15期数据进行滤波处理，计算滤波值与实测值之差，比较数据见表2；第2步是对后6期数据进行滤波预测，计算预测值与实测值之差，比较数据见表3。

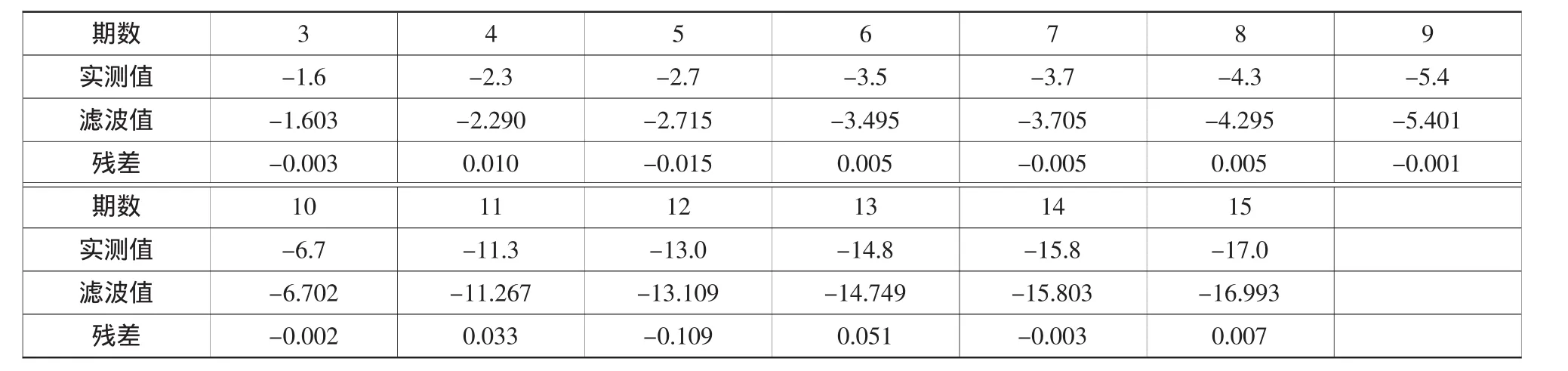
表2 前15期数据实测值与滤波值之差计算表Table 2 The difference between the observation value and the filtering value of the first 15 data mm

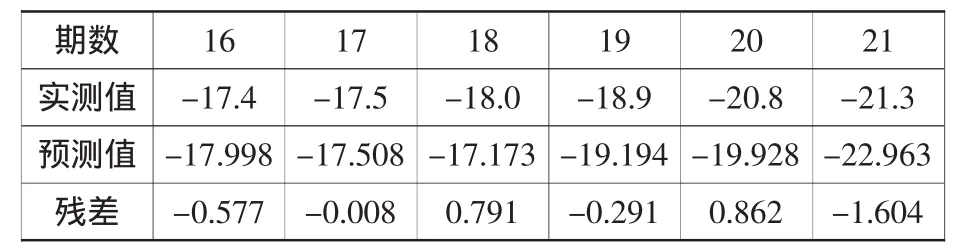
表3 后6期数据实测值与预测值之差计算表Table3 Thedifferencebetween theobservation data and theforecast data of thelast 6 data mm

另外，对数据进行五次多项式拟合分析，并将观测值、滤波值及多项式拟合值进行作图比较，形成图形见图1。

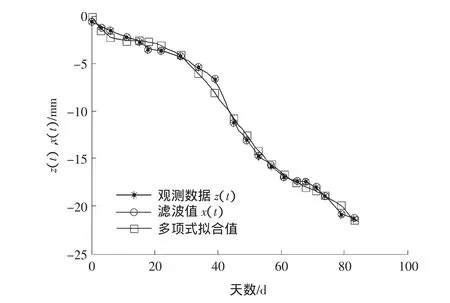
图1 滤波值与五次多项式拟合值比较图Fig.1 Comparison chart of filtering value and five polynomial value

4 结语

通过实例计算和分析后得到以下结论：

1）卡尔曼滤波是一个不断的预测、修正的过程，修正由于噪声引起的数据突变，使数据更符合实际变形趋势，并且只要有新的测量成果，就可以进行滤波处理，计算出最新的滤波值，便于实时处理观测值。

2）卡尔曼滤波值在原始数据基础上进行修正得到的最优估计值偏离原始值很小，则在考虑没有观测错误和粗差的情况下，所建立的滤波模型是合理的，可靠的，它能较好地模拟动态系统的变化规律，能有效改善原始观测数据的精度。

3）从表2数据分析，卡尔曼滤波值与观测值之间最大差值为12期的0.109 mm，其余差值均小于0.1 mm，说明卡尔曼滤波能较好地反应出暗埋段实际的沉降情况，对沉降监测能有效剔除噪声的作用。

4） 通过表3可以看出，预报值偏差最大为-1.608 mm，最小为-0.008 mm，说明卡尔曼滤波具有较强的预报作用。

5）从图1中滤波值与多项式拟合比较不难看出，滤波值与观测值重合度高，而五次多项式拟合值偏离观测值大小不一，说明滤波值比多项式拟合的精度要高。