基于模糊层次评价法的动力定位系统综合评价

冯宏伟，何祖军，杨奕飞

(江苏科技大学 电子信息学院，江苏 镇江212003)

0 引 言

随着人类对海洋资源需求的日益增长，传统的锚泊定位由于其成本受水深的影响，锚泊定位船舶在深海作业时精确定位具有极大的困难，已经不能满足深海作业的定位要求。动力定位系统是一种采用推进器来抵抗风、浪、流等环境干扰力的定位系统，由于其定位精准，成本不受水深限制以及可靠性良好等优点［1］，广泛地应用于铺管、采砂、半潜平台等领域。目前国内关于动力定位系统的研究取得了显著的阶段性成果。

文献［2］在分析推力器分配算法的基础上对动力定位系统定位能力极限进行了定性分析，文献［3］将神经网络算法融入了动力定位系统控制器的设计，文献［4］用模型试验的半理论半经验方法对推进器推力损失进行了计算，文献［5］采用并行分布补偿技术对动力定位系统的控制器进行了分析与设计，文献［6］基于最优控制原理对动力定位系统的节能特性进行了探讨，文献［7］使用粒子群优化算法设计了动力定位系统的自适应观测器。文献［8］运用故障树分析法对动力定位系统控制器进行了定性分析与评估。由于国内对动力定位系统的研究工作起步较晚，利用哪些指标以及如何对系统的整体性能进行评价等问题还有待深入探究。

从相关领域的研究现状来看，目前对动力定位系统综合评估的研究尚为空白。本文根据动力定位系统的可靠性、可用性以及可维护性即RAM［9］三个方面建立了动力定位系统的综合评估指标，并运用层次分析法确定各指标的权值，模糊综合评判算法对系统RAM 效能进行了全面的评价。最后针对最大隶属度结果与评分法可能出现的不同问题进行了讨论，并通过算例验证了评估的有效性。

1 动力定位系统RAM 评估指标体系的选取

通过对动力定位系统的认真分析，依据系统性、客观性、完备性的原则，构建了动力定位系统RAM指标体系及度量标准，如表1 所示。

表1 动力定位系统RAM 指标体系Tab.1 The RAM index system of dynamic positioning systems

系统可靠性:系统在规定时间间隔内完成预定的定点控位、首向控制以及航迹控制3 方面任务的能力。其中系统易恢复性是指在定位失效的情况下，系统重建并恢复船舶定位的能力。系统失效率是指系统正常工作的情况下，相临单位时间内船舶定位能力的失效概率。系统容错能力是指系统出现故障情况下，船舶保持其规定运行状态的性能。平均故障率是指系统平均故障间隔时间的倒数。

系统可用性:动力定位系统船舶在海洋环境干扰中作业时，系统有效、高效并且满意的达成特定目标的程度。其中服务完备性是指动力定位系统能满足海洋作业船舶定位需求的程度。功能准确性是指动力定位系统提供具有所需的定位能力极限和精度的结果的能力。平均可用时间是指动力定位系统能持续的提供船舶所需的定位能力。系统易操作性是指在规定条件下系统能被船员操作控制的容易程度。

系统的可维护性:动力定位系统发生故障时可被分析、修复和完善的能力。其中系统易分析性是指动力定位系统可被诊断故障原因或标识系统缺陷部分的能力。故障修复时间是指发生故障时，从发现故障开始到排除故障所用的时间。系统可扩展性指的是系统根据海洋环境或动力定位船舶的需求增加或减少其自身设备的性能。系统稳定性是指动力定位系统避免由于修复和扩充系统设备而造成意外结果的能力。

2 建立动力定位系统RAM 评估模型

评语集是在评估某一项指标时，将可能出现的评估结果划分为若干个等级，这些等级构成的集合就是评语集［10］。因素集与评语集的模糊关系矩阵即模糊矩阵Ri=(rij)n×m，其中rij为第i 个因素对评语集V 中等级vj的隶属度，其计算公式为:

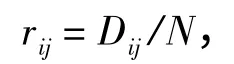
式中:Dij为第i 个因素被评为等级vj的人数;N 为评估成员总人数。

一级指标的评估公式为:

式中:Ai=(ai1，ai1，…，ain)为二级指标的权重向量;Ri=(rij)n×m为二级指标的模糊矩阵。一级指标效能评价结束后，将Bi(i = 1，2，3)视为模糊矩阵R 的评价向量，即R=［B1B2B3］T，假设一级指标权重为A=(a1，a2，…，an)，则动力定位系统RAM 评价公式为:E= A·R= (b1，b2，…，bn)，其中bi表示RAM 评估结果被评为vi的隶属度。评语量化公式为P=E·VT，式中VT为评语等级量化向量。

3 算例分析

将评价结果分为:V={好、较好、一般、差}，同时依次赋值{0.9，0.7，0.5，0.3}。采用1 ～9标度法表示指标间的相互重要性［11］，经专家小组对各级指标的综合评判后得各指标的权重。以下仅以一级指标为例，其对比矩阵如表2 所示。

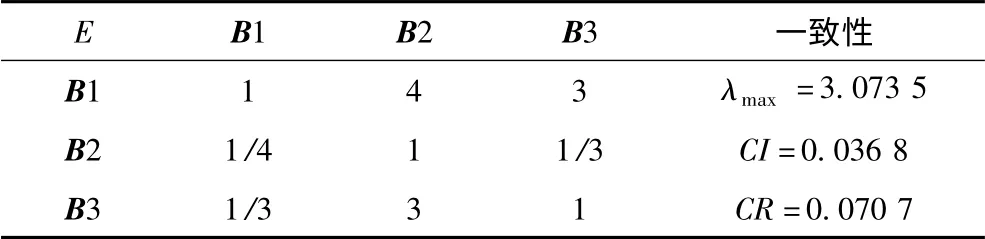
表2 动力定位系统RAM 一级指标判断矩阵Tab.2 The level indicators of RAM of dynamic positioning systems

其特征向量，即一级指标权重向量为:

同理可得二级指标权重向量:

根据专家组对指标认真评估、分析，经归一化得表3。

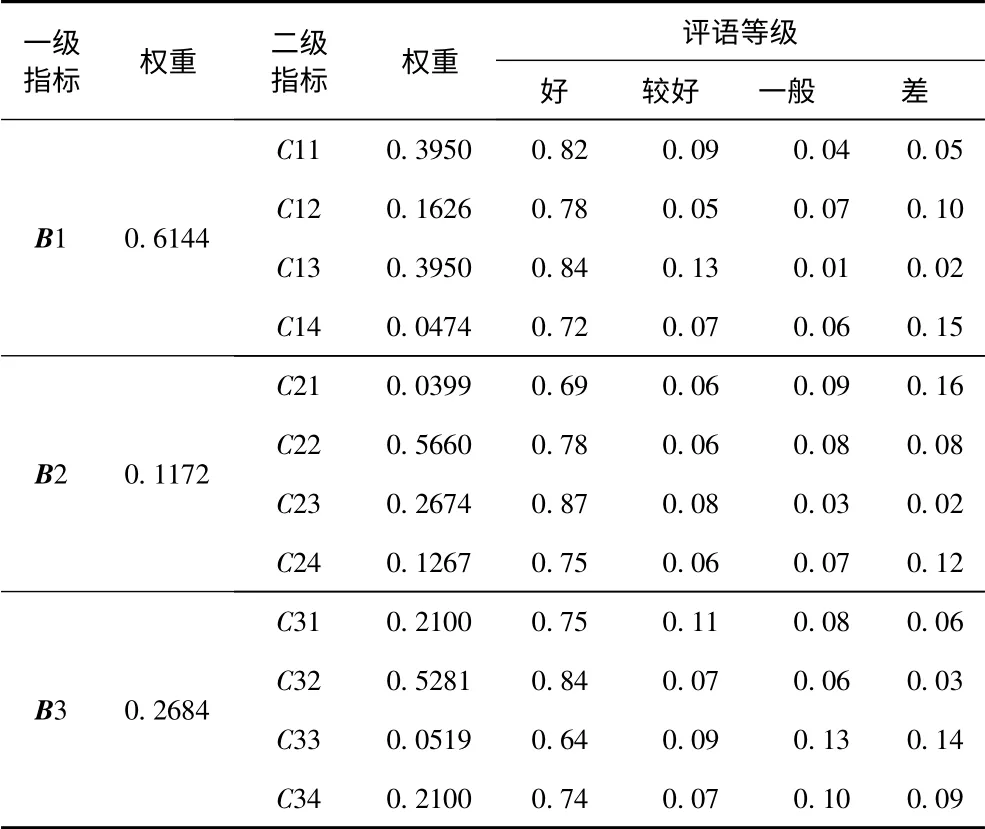
表3 权重与隶属度数据表Tab.3 The weight and membership degree

由表3 可得隶属度矩阵:

最后根据上述数据，对动力定位系统RAM 进行综合评价:

根据隶属度最大原则，该耙吸式挖泥船的RAM综合评价等级为好。

4 评估结果的分析

根据模糊综合评价法的最大隶属度原则，该挖泥船的RAM 综合评估等级为“好”，而结合评语等级的量化向量进行评估时，会发现模糊综合评估结果量化后得分为

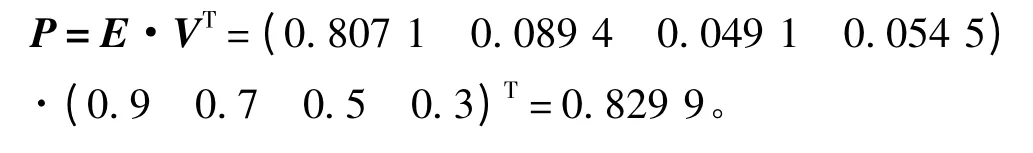
表4 评估结果参考标准标Tab.4 Reference standard of the evaluation results

由表4 可知，评判结论为“较好”。可以发现，不同的评价方法有可能得到相同或不同的评估结果。针对可能出现的不同情况，本文分以下2 种情况对最终评估结果的选择进行讨论:

1)若根据最大隶属度原则得出的结论=评语等级量化评估结论，则模糊综合评估结果即为最终评估结论。

2)若根据最大隶属度原则得出的的结论≠评语等级量化评估结论，则

①存在1 个以上(包括1 个)的隶属度与最大隶属度近似，如E=［0.31 0.33 0.32 0.04］，根据最大隶属度原则评价结果应该为较好，然而综合评价结果P=E·VT=0.682 0，根据表3 可得评估结果为“一般”。这时可看出，0.31 和0.32 均与最大隶属度相似，这时模糊综合评价结果存在不确定性，所以最终结果选择评语等级量化结论“一般”。

②最大隶属度明显大于其余隶属度时，如本题算例所示E=(0.807 1 0.089 4 0.049 1 0.054 5)，采用评语等级量化结论为一般显然不够合理，最大隶属度所对应的评价结论即为最终结论。

5 结 语

本文建立了动力定位系统可靠性、可维修性和可用性指标体系，并利用模糊数学中隶属度理论与层次分析法相结合的评价方法，有效避免了加权过程中主观因素的影响，弥补了AHP 法的不足，并对最终结论的选取进行了分析，让评估结果更接近系统的真实情况，为今后动力定位系统整体评价的展开提供了依据。

［1］ASGEIR J S． Structural issues in the design and operation of marine control systems［J］． Annual Reviews in Control，2005(29):125 －149．

［2］张峥．某型救生船的流体动力性能和动力定位能力评估［J］．船舶，2007(3):19 －23．ZHANG Zheng． Hydro dynamic aspects and DP capability evaluation of one salvage vessel［J］．Ship＆Boat，2007(3):19 －230．

［3］FANG M，LEE Z． Portable dynamic positioning control system on a barge in short-crested waves using the neural network algorithm［J］． China Ocean Engineering，2013，27(4):469 －480．

［4］广超越，罗薇．船舶动力定位系统推进器推力损失计算［J］．武汉理工大学学报(交通科学与工程版)，2012，36(5):1074 －1078．GUANG Chao-yue，LUO Wei．Calculation of thrust losses in dynamic positioning system ［J］． Journal of Wuhan University of Technology (Transportation Science ＆Engineering)，2012，36(5):1074 －1078．

［5］YE Bao-yu，WANG Qin-ruo，XIONG Jian-bin，et al．Parallel distributed compensation fuzzy controller design for dynamic positioning［J］．EN，2012，7(15):409 －418．

［6］邢雪林，陈德兴，彭霞，等．船舶动力定位系统技术节能分析探讨［J］．交通节能与环保，2009(4):18 －21．XING Xue-lin，CHEN De-xing，PENG Xia，et al． Study on energy-saving technologies for dynamic positioning system［J］． Energy Conservation ＆ Environmental Protection in Transportation，2009(4):18 －21．

［7］LIN Xiao-gong，XIE Ye-hai，ZHAO Da-wei，et al．Estimation of observer parameters for dynamic positioning ships［J］．Mathematical Problems in Engineering，2013．

［8］刘杨．动力定位控制系统故障模式与影响分析［D］．哈尔滨:哈尔滨工程大学，2011．LIU Yang．Research on dynamic positioning control system based on failure mode and effects analysis［D］． Harbin:Harbin Engineering University，2011．

［9］SIKOS L，KLEMES J．CAPE contribution to availability and reliability of waste to energy［J］．Computer Aided Chemical Engineering，2009(26):1251 －1255．

［10］蒋胜平，孙华付，汪清园． 基于二级综合模糊评判的指挥信息系统综合效能评估［J］．舰船电子工程，2012，32(4):36 －38，73．JIANG Sheng-ping，SUN Hua-fu，WANG Qing-yuan．Effectiveness of command and information system based on secondary general fuzzy comprehensive evaluation［J］．Ship Electronic Engineering，2012，32(4):36 －38，73．

［11］BOUTHINNIER V，LERIS A H． Effectiveness analysis of C2 system ［J］． IEEE Trans on System， Man and Cybernetics，Jan/Feb，1984．