多产品报童模型的研究综述

王东红 WANG Dong-hong

（广西财经学院 管理科学与工程学院，广西 南宁530003）

(School of Management Science and Engineering, Guangxi University of Fiance and Economic, Nanning 530003, China)

0 引 言

报童模型（Newsvendor Problem，NP） 是一个考虑单周期、随机需求的经典库存模型。自从该模型被提出以后，便成为库存理论研究的焦点之一，在现实生活中得到了广泛的推广和应用，例如，报刊杂志、果蔬、数码类电子产品、时尚产品以及酒店客房和航空机票的经销订购等问题；理论界也涌现了大量的对报童模型及其扩展模型问题的研究文献和综述。Khouja[1]对经典的报童模型及它的11 种扩展做了一个非常全面的综述，总结了从20 世纪50 年代至1999 年以来相关文献的主要贡献和模型的扩展研究。例如扩展到不同的目标和效用函数；扩展到不同的供应商定价策略；折扣问题；需求规律和信息的缺乏度；随机产出以及带资源约束的多产品库存问题；可替代多产品方面的扩展；多层次系统方面的扩展；多场所系统方面的扩展；销售季节多阶段备货方面的扩展及其他方面的扩展，并提出了进一步的研究方向，认为将上述扩展的两个或多个相结合对报童模型来说会更加实际。

随着生产技术的进步和销售环境的复杂化，多产品的生产经营顺应了现实的决策环境而产生，多产品报童模型也被众多研究者关注。本文综合分析了多产品报童模型的研究文献，主要从不考虑定价的多产品报童模型研究和考虑定价决策的多产品报童模型研究两个方面对多产品报童模型的研究进行综述，挖掘文献中所提出的新的研究视角和解决方法，并提出对多产品报童模型的进一步研究的方向。

1 多产品报童模型

自从Hadley 和Whitin[2]在1963 年首次将经典报童模型扩展到带有约束下的多产品报童模型（Multi-Product Newsvendor Problem, MPNP），在求解这些模型的时候采用了拉格朗日算子（Lagrange Multipliers） 莱布尼兹规则（Leibniz Rule） 和动态规划方法（Dynamic Programming）。他们证明了当考虑单资源约束时，动态规划可以用于求解得出整数值的解，然而，他们注意到，当增加约束到模型中后，用动态规划法就很困难。自此，很多学者对MPNP 进行了深入的研究和推广，如将市场因素中预算限制、生产外包、供应商数量折扣、损失最大限制、预售策略、价格协议、产品可替代等引入到多产品报童模型中，丰富和发展了多产品报童模型的研究。读者可参看Gallego 和Moon[3]和Khouja[1]，了解更多的对报童问题的扩展研究。

George[4]研究了一个不确定需求下的考虑预算约束的鲁棒（Robust） 报童模型。传统描述需求不确定的方法是概率分布函数，他采用了一个确定的优化模型，用两种类型即分段和离散情况来描述需求不确定性。对分段需求情况仅需要不确定需求的一个下界和上界，而对于离散需求的情况需要一系列每个产品的相似的需求结果。利用上述两种类型描述需求不确定性，采用几个极小极大化遗憾公式表达（Regret Formulations） 一个预算约束下的多产品报童模型。对于分段需求情形，他提出了一个线性时间优化算法；对于离散需求情形，他证明了这是一个NP-hard 问题，并通过动态规划方法求解。最后，他认为一部分产品的需求是分段式的，另一部分产品的需求是离散式的，两种情形进行混合，扩展了模型的研究。

Moon 和Silver[5]研究了对补货数量总价值有预算约束的多产品报童模型，且考虑补货的固定成本。他们利用动态规划法进行求解，并提出了简单而有效的启发式算法。Abdel-Malek 和Montanari[6]提出了一种利用严格的、近似的及遗传迭代算法的方法求解单种约束下的多产品报童问题。Abdel-Malek 和Areeratchakul[7]提出了一个采用二次规划方法求解多种约束下的多产品的报童模型。他们利用Excel Solver 和Lingo 等线性规划软件求解出多种约束下报童模型，并依赖于需求分布函数的类型得出了精确的和好的近似解。还解决了产品的需求正偏态概率密度函数的复杂性，忽略了其下限可能导致负的最优解，或一些产品订购量的不可行数量，如同Lau 和Lau[8-9]最早所观察到的一样。

Abdel-Malek 和Montanari[10]研究了一个在预算约束下的多产品的报童模型问题。Abdel-Malek 和Montanari[11]提出了一个方法来研究具有两种约束下的多产品报童模型解空间的对偶问题并给出了一个得出每种产品的最优批量的方法。该方法采用了拉格朗日算子（Lagrangian Multipliers），莱布尼兹规则（Leibniz Rule） 和KKT 条件（Kuhn-Tucker Conditions）。且有必要在求解最优解或近似最优解时将他们集成进行迭代求解。他们所研究的方法最重要的一个特征就是可以适用于一般分布的需求函数。

Zhen Shao 等[12]研究了一个预算约束下模糊需求的多产品报童模型。他们认为既然在现实生活中需求是模糊的，那么报童的利润也是模糊的。他们根据决策的标准不同，研究了三类模型：Expected Profit Model, the Most Profit Model 和α-Profit Model，即从最大化期望收益、机会约束规划、机会规划这三个方面建立了新的模型。并采用了基于遗传算法及模糊模拟的混合智能算法求解新的模型。

Niederhoff[13]区别于前期学者在研究中试图采用拉格朗日松弛算法或有限需求分布的方法求解多产品报童模型，进而提出了一个近似规划法求解多产品报童模型，其中产品的需求相互独立，库存产品数量受两个或更多的线性约束，例如预算或容量约束，并用凸规划理论得出一个最优近似解。

Abdel-Malek 等[14]将多产品报童模型扩展到了随机产出情形下的模型。他们指出该模型就像一个园丁问题（the Gardener Problem）。他们采用了拉格朗日算子（Lagrange Multipliers） 莱布尼兹规则（Leibniz Rule） 和牛顿法（Newton's method） 求解在随机产出和随机需求情形下的最优解。他们所研究的方法适合于一般概率分布的函数，所给出的例子证明了该方法在相互依赖的产出结构下对不同的供应和需求概率分布的适用性。

Jafar Rezaei 等[15]研究了一个供应链中有多种产品和多个供应商的情形下，且每个供应商都是有限的产能。他们假定从供应商处收到的产品不全是质量好的产品。存在质量缺陷和不一定有缺陷的产品可以用于另一个库存情况。在下次发货之前，有质量缺陷的产品作为一批次以优惠价格销售出去。在有限的计划期间内需求是已知的，且在一个多周期内可以确定一个最优的采购策略。决策者及购买者需要做出决定订购什么产品，订购多少，向谁订货，在哪个周期内订购等问题。最后，他们采用一个遗传算法（Genetic Algorithm, GA） 对模型求解。

2 多产品联合定价的报童模型

近年来，学者对经典报童模型考虑了定价决策问题进行模型扩展研究。Whitin[16]最早对报童模型的研究考虑到了定价决策问题，他主要研究了在不确定需求环境下同时决策库存数量和销售价格优化问题，Mills[17], Karlin 和Carr[18]也做了类似的研究。Petruzzi 和Dada[19]对单产品报童模型的定价问题进行了一个全面的综述并提出了一些有意义的扩展，他们对一个两周期/两个市场零售情况下的联合库存和定价决策的报童模型进行研究。Karakul[20]研究了在一个出清市场上时尚产品的联合定价和采购策略。Granot 和Yin[21]分析了采用乘法式的、加和式价格依赖的需求，分析了一个集中的报童模型的定价和订购延迟的效果。Chen 和Bell[22]研究了当消费者退货时的联合定价和库存补货决策。Pan 等[23]构建了一个两阶段模型，对需求随机和降价环境下一个供应链中地位占优的零售商联合定价和订购策略。He 等[24]考虑了需求不确定，且需求对零售价格和销售努力敏感下的报童模型的扩展问题。由于报童定价问题可以协调供应链系统的收益和市场需求不确定环境，近年来受到越来越多地关注，但是，目前大多数文献探讨其在不同的供应链环境下的应用并获得了一些管理的见解。

最近几年，有不少学者从不同角度对多产品的生产、库存、定价和分类（Assortment） 规划决策问题对报童模型进行扩展研究。Bertsimas 和Boer[25]研究了一个周期性多产品定价和库存控制问题在生产计划和航空收益管理中的应用。他们证明了在需求分布是确定类型时，单周期模型的目标函数是凸函数，从而对大多数情况都是容易求解的。而对更加复杂的多周期问题，他们提出了一种结合线性和动态规划的启发式算法求解。其中，数值试验和理论在最优期望收益方面的验证表明了一个基于随机模型的动态策略优于一个基于确定模型的简单的静态的策略，而确定性模型是依赖于通过变异系数（the Coefficient of Variation） 衡量的需求可变性的水平。

Adida 和Perakis[26]研究了一个有限期间的离散时间模型。他们把一个鲁棒优化方法（A Robust Optimization Approach） 引入到“Make-to-Stock”的生产系统的动态定价和库存控制问题的一个流模型中。对每个时间t的产品i，给定的输入包括每单位的库存持有成本hi（t），生产成本fi（·），需求函数di（t），初始库存水平和共享的产能率K（t）。然后确定N个产品在给定时间期间[0,T]内的价格｛pi（t）｝，生产流程率｛ui（t）｝和库存水平｛Ii（t）｝，通过最小化dt，约束条件为和对控制变量和需求函数的标准的非负约束。用一个确定的扰动表示需求的不确定性，用的参数约束在一个不确定集。最后，他们讨论了一些简单的模型和一些理论及数值算例。

Bernstein 和Federgruen[27]分别研究了在集中供应链和分散供应链情景下的模型。在集中供应链系统中，一个决策者（供应商） 假定对所有零售商的价格，销售量和补货策略进行决策，而在分散供应链系统中，供应商基于零售商（每个零售商都是最大化自己的利润） 的订单，对其批发价格机制和补货策略决策。利润函数依赖于补货策略和几个成本因素，包括供应商和零售商之间固定的和变动的配送成本，库存年持有成本和管理一个零售商账目所发生的年费用。与上述文献内容相似，Bernstein 和Federgruen[28-30]假定一个供应商服务于多个网络分布的零售商，但仅仅是一个分散的供应链系统。Bernstein 和Federgruen[30]研究在每周期开始，每个零售商选择他自己的零售价格pi和从供应商处的订购量yi，每单位产品批发价格wi。过量的库存由供应商以每单位产品bi的价格回收。因此，零售商i的期望利润函数为：其中，p是所有零售商的价格向量是零售商在价格p时的随机向量，且

Bernstein 和Federgruen[28-30]扩展了Bernstein 和Federgruen[30]中的模型到周期检查、无限期的模型，每个零售商面临最大化其长期的利润。零售商面临着一个时间上相互独立的需求的流，而不是各零售商的需求相互独立。在每个周期结束，库存可以每单位成本结转到下一个周期，而不足的库存和延迟交货（backlogged） 的单位成本为

因此，Bernstein 和Federgruen[28]中的单阶段的利润函数是：

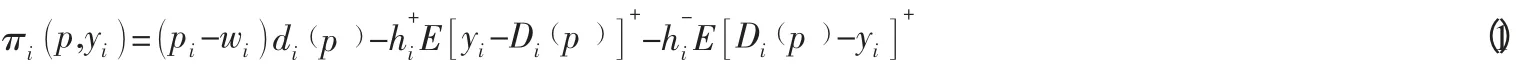
其中，Di（p）是每个零售商i在价格p时的期望需求（或销售量）。

Bernstein 和Federgruen[29]在模型中考虑了服务竞争，其中，需求也依赖于f，fi是每个阶段零售商选择的目标服务水平，或补充率（fill rate）。

零售商i的利润函：

价格和补充率限制在一个集中。他们讨论了三种竞争情况：价格竞争，价格和服务竞争，两阶段竞争（所有竞争者首先选择一个服务水平，之后同时选择定价和库存策略以应对所选择的服务水平）。

Maddah 和Bish[31]研究了从一组可能的变量中组成的一个产品线的联合定价和库存决策问题。假定S⊆Ω 是一组存储的产品。对产品S的需求从顾客在单个销售周期到达一个零售商店中获得。他们的模型可以被看成是一个联合定价和分类决策多产品报童模型（Multi-Item Newsvendor Model）。定义为顾客在一个价格向量p（对S中所有的产品） 购买产品i∈S；λ 是顾客到达商店的平均值；c是产品1,…,S的成本向量和Φ（·）分别是标准正态分布的概率密度函数和分布函数（假定需求服从正态分布）。

Hopp 和Xu[32]采用一个基于价格和缺货替代下的近似模型，分别在集中和离散系统下分析库存、定价和分类决策问题。Aydin 和Porteus（2008）[33]研究了在报童模型中在一个给定的分类（assortment） 的多产品库存水平和定价的优化问题。除了定价和库存决策外，他们还考虑了分类选择的问题。他们研究的是单周期，需求随机，并且是基于价格替代而非缺货替代情况下优化模型。受市场份额模型（market share models） 通常用于市场营销中的驱动，他们解决需求模型包括乘法式的不确定性。模型中pi和ci是每单位产品i的销售价格和生产成本。是价格向量库存水平向量。Di（p）是给定价格向量p下对产品i的需求；分布是需求Di（p）的分布函数（c.d.f）和概率密度函数（p.d.f）； 假定关于x严格递增。公司希望最大化利润函数：

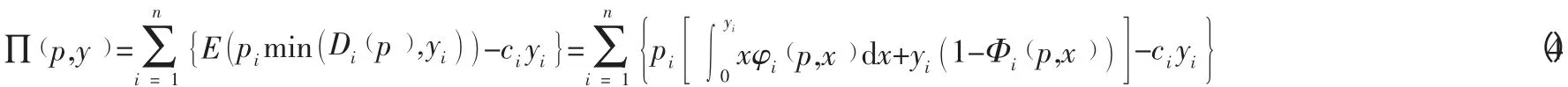
因为∏p,（y）在yi是可分的和凹的，最优库存水平可表示为对作为通常的临界分位数的每个价格向量p是给定的。问题就可以写成以下方程（例如：Porteus[34）]：研究的焦点放在了价格对库存水平的影响问题上。他们发现在一定程度上目标函数依然表现相当好，对一阶条件存在一个唯一解，对于他们所研究的问题，这个解是最优的。

Guoqing Zhang[35]研究了一个供应商数量折扣和预算约束下的多产品报童模型，与前期的非线性优化模型不同，由于价格折扣，他们将问题用混合整数非线性规划模型表达，目标函数是最大化期望利润，即：

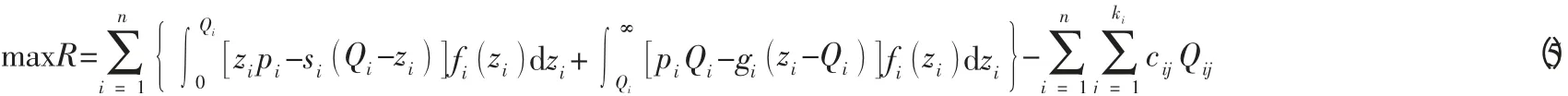
Jianmai Shi 等[36]在报童模型的基础上考虑零售商的定价决策和供应商的数量折扣问题的多产品的定价策略。供应商对所有产品提供数量折扣，需求函数假定是线性的，价格依赖型的加和式的随机性，即其中Di（p）=ai-bi pi是产品i的平均需求，ui是在之间的已知分布的随机变量零售商的目标是在多种容量的约束下，通过联合决策多产品的订购数量和销售价格以达到利润最大化。他们建立了一个扩展的离散规划模型（Generalized Disjunctive Programming,GDP）：

模型的约束条件考虑到了供应商数量折扣约束，他们开发了一个拉格朗日（Lagrangian） 启发式算法求解模型。通过一个随机的生产1 000 种产品的实例验证了所提出的方法，计算结果表明拉格朗日启发式算法对所有的例子都能在一个合理的时间内给出一个非常好的解。

Murray 等[37]结合报童模型考虑购买者的预算敏感性，研究了销售商（Newsvendors） 销售多产品时的订购和定价策略（the Multi-Product Price-Setting News-Vendor Problem，MPPSNVP）。其中每种产品的随机特征依赖于其他的产品，即交叉弹性。目标函数包括销售产品所得利润以及为销售出产品产生的损失，即：

其中，p和q是决策向量是产品i的需求的累积分布函数优化模型的最优决策是最大化约束条件考虑到产品量的上下限约束及资源约束，例如预算和空间的约束等。另外，考虑到每个产品的价格选择可以在一个离散的集中，订购量是一个整数。作者将目标函数转换成一个整数规划求解，并开发了一个基于Nelder-Mead 搜索技术的数值优化程序，从一些小规模和大规模数值算例中获得令人鼓舞的数值结果。论文是首次将这个情况结合到消费者的预算敏感性，即消费者在购买产品的时候需要考虑自己当前的经济状况。

许多学者对多产品报童模型的研究做了大量深入的探讨，构建了许多量化模型，考虑了需求不确定情况下的库存控制策略和联合定价与库存控制策略。学者们也提出了许多求解方法，包括动态规划法等，但大多是采用启发式算法求解模型，例如启发式算法Erlebacher[38]，动态规划法Moon 和Silver[5]，遗传迭代模型Abdel-Malek 等[6]和二进制算法Zhang 等[39]等都有一定的研究，得出最优策略的解或近似解。尽管多产品报童模型（Multi-product Newsvendor Problem, MPNP） 的求解算法得到了广泛的研究，但大多数所提出的模型和求解方法通常只能求解包括大约10 种产品的模型。Lau 和Lau[8-9]是在所研究多产品报童模型的文献中，极少有地提出了求解包括上千种产品的模型。

3 研究存在的问题及展望

3.1 考虑时间因素

需求的不确定性给企业的决策带来了很大的困难，市场的变幻莫测也使得价格成为了影响企业库存管理的重要因素，因此，如果将需求、价格与时间因素结合起来对多产品的库存管理进行研究，将更有利于企业科学的管理决策。

3.2 考虑电子商务环境

电子商务时代，市场需求变化的速度更快，更加难以确定，采购与库存管理的复杂性大大增加。考虑报童模型的鲁棒性，对电子商务环境下的多产品库存管理进行定量分析研究，将会是进一步研究的热点。

3.3 考虑供应链竞争因素

由于竞争日益剧烈，单个企业难以应对市场的变化，供应链的合作和竞争成为了必然趋势，因此，研究供应链多层次及网络式的多产品报童模型无疑是实践或理论界的一个热点。

3.4 计算复杂性和精确性

虽然计算机技术和算法技术的发展对库存管理的发展起到了极大的推动作用，然而现实的复杂性难以用理想的模型描述，因此，在一定假设条件下提出的考虑多种市场因素、多种产品的报童模型的计算将会是极其复杂的，尽管现有一定的启发式算法可以求出问题的近似解或确定解的上下界，但很难确定其精确性，因此，开发出更先进的算法也必将对贴近现实的多产品报童模型的求解至关重要。

4 结 论

随着对报童模型更加贴近实际角度的研究进展，多产品报童模型的研究对企业的管理决策提供了更好的指导。相关研究的进程也见证了报童模型随着时代变化而发展的一个过程，未来的研究中，报童模型将继续在实践和理论界实现其不可替代的指导价值。

[1] Khouja, M. The single-period（new-vendor）problem: literature review and suggestions for future research[J]. OMEGA Int. J.Manage Sci, 1999,27:537-553.

[2] Hadley, G. Whitin, T. Analysis of Inventory Systems[M]. Prentice-Hall, Englewood Cliffs, NJ, 1963.

[3] Gallego, G., Moon, I. The distribution free newsboy problem: Review and extensions[J]. Journal of the Operational Research Society, 1993,44:825-834.

[4] George L. V. Robust multi-item newsboy models with a budget constraint[J]. Int. J. Prod. Econ, 2000,66:213-226.

[5] Moon I, Silver E. A. The Multi-Item Newsvendor Problem with a Budget Constraint and Fixed Ordering Costs[J]. The Journal of the Operational Research Society, 2000,51(5):602-608.

[6] Abdel-Malek, L.L., Montanari, R. Morales. L.C. Exact, Approximate and Generic Iterative Models for the Multi-Product Newsboy with Budget Constraint[J]. International Journal of Production Economics, 2004,91:189-198.

[7] Abdel-Malek, L.L., Areeratchaku, N. A quadratic programming approach to the multi-product newsvendor problem with side constraints[J]. European Journal of Operational Research, 2007(176):1607-1619.

[8] Lau, H., Lau, A. The multi-product multi-constraint newsboy problem: application, formulation and solution[J]. J. Oper. Manage, 1995,13:153-162.

[9] Lau, H., Lau, A. The newsstand problem: a capacitated multiple-product single-period inventory problem[J]. Eur. J. Oper.Res, 1996,94:29-42.

[10] Abdel-Malek, L.L., Montanari, R. An analysis of the multi-product newsboy problem with a budget constraint[J]. Int. J.Prod. Econ, 2005(97):296-307.

[11] Abdel-Malek, L.L., Montanari, R. On the multi-product newsboy problem with two constraints[J]. Comput. Oper. Res, 2005(32):2095-2116.

[12] Zhen Shao, Xiao yu Ji. Fuzzy multi-product constraint newsboy problem[J]. Appl. Math. Comput, 2006,180:7-15.

[13] Niederhoff, J.A. Using separable programming to solve the multi-product multiple ex-ante constraint newsvendor problem and extensions[J]. Eur. J. Oper. Res, 2007,176:941-955.

[14] Abdel-Malek, L.L., Montanari, R., Meneghetti, D. The capacitated newsboy problem with random yield: The Gardener Problem[J]. Int. J. Prod. Econ, 2008,115:113-127.

[15] Jafar Rezaei, Mansoor Davoodi. A deterministic, multi-item inventory model with supplier selection and imperfect quality[J].Applied Mathematical Modelling, 2008,32:2106-2116.

[16] Whitin, T. M. Inventory control and price theory[J]. Management Science, 1955(2):61-68.

[17] Mills, E. S. Uncertainty and price theory[J]. Quart. J. Econom, 1959,73:116-130.

[18] Karlin, S., Carr, C. R. Prices and optimal inventory policy. Studies in Applied Probability and Management Science[M].Stanford University Press, Stanford, CA, 1962.

[19] Petruzzi, N.C., Dada, M. Information and inventory recourse for a two-market, price setting retailer[J]. Manuf. Serv. Oper.Manage, 2001,3:242-263.

[20] Karakul, M. Joint pricing and procurement of fashion products in the existence of clearance markets[J]. Int. J. Prod. Econ,2008,114:487-506.

[21] Granot, D., Yin, S. Price and order postponement in decentralized newsvendor model with multiplicative and price-dependent demand[J]. Oper. Res, 2008,56:121-139.

[22] Chen, J., Bell, P.C. The impact of customer returns on pricing and order decisions[J]. Eur. J. Oper. Res, 2009,195:280-295.

[23] Pan, K., Lai, K.K., Liang, L., Leung, S.C.H. Two-period pricing and ordering policy for the dominant retailer in a two-echelon supply chain with demand uncertainty[J]. Omega, 2009,37:919-929.

[24] He, Y., Zhao, X., Zhao, L., He, J. Coordinating a supply chain with effort and price dependent stochastic demand[J]. Appl.Math. Model, 2009,33:2777-2790.

[25] Bertsimas, D., Boer, D. S. Dynamic pricing and inventory control for multiple products[J]. Journal of Revenue and Pricing Management, 2005,3(4):303-319.

[26] Adida, E., Perakis, G. A robust optimization approach to dynamic pricing and inventory control with no backorders[J]. Math. Prog, 2006,107(1):97-129.

[27] Bernstein, F., Federgruen, A. Pricing and replenishment strategies in a distribution system with competing retailers[J]. Oper.Res, 2003,51(3):409-426.

[28] Bernstein, F., Federgruen, A. Dynamic inventory and pricing models for competing retailers[J]. Naval Res. Logist, 2004,51(2):258-274.

[29] Bernstein, F., Federgruen, A. A general equilibrium model for industries with price and service competition[J]. Oper. Res,2004,52(6):868-886.

[30] Bernstein, F., Federgruen, A. Decentralized supply chains with competing retailers under demand uncertainty[J]. Manage. Sci,2005,51(1):18-29.

[31] Maddah, B., Bish, E. K. Joint pricing, assortment, and inventory decisions for a retailer's product line[J]. Naval Research Logistics, 2007,54:315-330.

[32] Hopp, W. J., Xu, X. A static approximation for dynamic demand substitution with applications in a competitive market[J].Oper. Res, 2008,56(3):630-645.

[33] Aydin, G., Porteus, E. Joint inventory and pricing decisions for an assortment[J]. Operations Research, 2008,56(5):1247-1255.

[34] Porteus, E. L. Foundations of Stochastic Inventory Theory[M]. Stanford University Press, Stanford, CA, 2002.

[35] Guoqing Zhang. The multi-product newsboy problem with supplier quantity discounts and a budget constraint[J]. European Journal of Operational Research, 2010,206(2):350-360.

[36] Jianmai Shi., Guoqing Zhang., Jichang Sha. Jointly pricing and ordering for a multi-product multi-constraint newsvendor problem with supplier quantity discounts[J]. Applied Mathematical Modelling, 2011,35:3001-3011.

[37] Murray, C.C., Gosavi, A., Talukdar, D. The multi-product price-setting newsvendor with resource capacity constraints[J]. International Journal Production Economics, 2012,138:148-158.

[38] Erlebacher, S.J. Optimal and heuristics solutions for the multi-item newsvendor problem with a single capacity constraint[J].Prod. Oper. Manage, 2000(9):303-318.

[39] Zhang, B., Xu, X., Hua, Z. A binary solution method for the multi-product newsboy problem with budget constraint[J]. Int.J. Prod. Econ, 2009,117:136-141.