压缩感知观测矩阵的优化算法

田香玲，席志红

(哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨 150001)

2004年 David Donoho、T．Tao等提出压缩感知理论［1－5］，之后又发表了诸多关于压缩感知的文章，对信号的稀疏表示、测量矩阵和重构算法等做了详细的描述，分析了l0范数和l1范数的关系，为重构算法的实现和改进提供了理论支持。

压缩感知理论包含3方面:信号的稀疏表示、观测矩阵的设计和重构方法。压缩感知理论的前提是稀疏表示，关键是观测矩阵的设计，核心是重构算法。压缩感知的理论思想是用远小于信号长度的观测值重构原始信号。这一理论打破了Nyquist理论对信号处理的束缚，是信号处理领域的一场革命。

目前，学者们已提出了众多重构算法及其改进算法，但观测矩阵的设计同样是压缩感知的重要部分，本文主要分析了观测矩阵存在的不足，针对信号稀疏表示之后的特点和观测矩阵的非相干性原则，提出一种新的算法，提高图像的重构精度。

1 压缩感知理论

压缩感知理论表明稀疏信号或在变换域稀疏的信号，可通过一个矩阵将测量值重构出原始信号。其不再基于Nyuist采样原则，在信号的频率域进行采样，而是基于信号的结构对信号压缩重构，所需的数据量大幅减少。

假设x∈RN×1是一个实值有限长的一维离散信号是 RN×1中的 N 个标准正交基，令 Ψ∈RN×N是以 Ψi为列向量的矩阵，即 Ψ=［Ψ1，Ψ2，…，ΨN］，则RN×1中的任意信号均可由正交基{Ψi}Ni=1线性表示

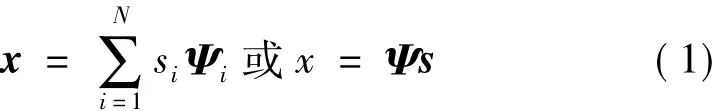
其中，si是内积 si=〈x，Ψi〉=ΨTix。实际上向量s是向量x等价表示，只是表达方式不同，x是时间域或空间域的，s是x的变换域表示。若s中只有K(K≪N)个值不为零，其余N－K个值均为零或近似为零，则称信号x是K－稀疏的［6］。

压缩感知的数学形式描述式(2)所示

将式(1)代入式(2)可得

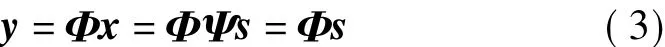
其中，Θ=ΦΨ，Θ∈RM×N称为观测矩阵或者信息算子。

对于M×N维的观测矩阵，其行数M远小于列数N，所以由y的M个观测值重构信号x是NP－hard问题。但若式(3)中s中仅有K个数是非零的，就可由y精确重构原始信号x。解式(3)的逆问题得到变换域Ψ的稀疏基的系数s，将系数s代入式(1)便可得原始信号x。因此，压缩感知的实质是:选择使信号最稀疏的稀疏基，用观测矩阵得到测量值，然后用重构算法准确快速稳定地重构出原始信号。

1．1 信号的稀疏表示

压缩感知的前提条件是信号的稀疏性或可压缩性［7］，但信号在有些基上可能是稀疏的，或是不稀疏的，即使是稀疏的，可能会在有些基上的稀疏性好，而有些稀疏性不好，而信号的重构精度与信号的稀疏度相关，所以选择合适的稀疏基极为重要。调和分析方法是常用的稀疏表示方法，其包括傅里叶变换、离散余弦变换和小波变换，其中小波基应用最为广泛;之后多尺度几何分析法和基于超完备的图像自适应稀疏表示方法相继被提出。

1．2 设计观测矩阵

观测矩阵对观测值的获取和信号的重构过程都具有较重要的作用，所以研究设计观测矩阵至关重要。对于K－稀疏矢量v，上述重构问题应满足的条件是

式(4)表明矩阵Θ必须满足K－稀疏矢量的长度，而矩阵Φ中的K个重要向量的位置也是未知的，所以如何确定观测矩对信号重构至关重要。假设Ψ中K个向量构造成观测矩阵Φ，但该种方法精确重构原始信号的概率仅为1/CKN，需尝试CKN次才能得到原始信号，所以计算量较大，且由于构造观测矩阵是随机选取向量，所以并不能保证观测矩阵的列向量就是稀疏系数s的非零系数对应的位置。因此，观测矩阵Φ与ΨH应极端不相似，即矩阵Φ和稀疏基Ψ的列不能相互线性表示。实际上，就是观测矩阵Φ满足约束等距特性(Restricted Isometry Property，RIP)［8］，RIP 性质定义如下:

设Φ为M ×N维矩阵，且 M≪N，T⊂{1，2，…，N}，T为集合T的势，对任意满足1≤K≤N的整数K，定义K－约束等距常数(K－Restricted Isometry Constants，K －RIC)为 δK，对任意T ×1维列向量c，以下不等式

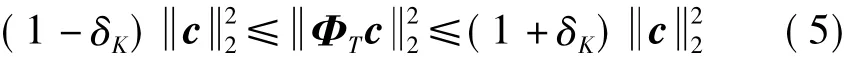
为对所有按T中的元素索引的矩阵Φ各列组成的子矩阵ΦT均成立的最小数。类似地，对满足K+K'≪N的整数 K、K'，定义 K、K'－约束正交常数(K，K'－Restricted Orthogonality Constants，K，K' － ROC) θK，K'为使得以下不等式

为对所有满足 T，T'⊂{1，2，…，N}且T≤K'，T'≤K的子矩阵ΦT，ΦT'都成立的最小数。式(5)则称为约束等距性质(Restricted Isometry Property，RIP)。

由上述理论可知，观测矩阵设计时必须满足RIP性质，这样才能获得包含较多信息量的信观测值，得到较高的重构精度。常见的测量矩阵分为随机观测矩阵和确定性观测矩阵。

1．3 重构算法

求解式(3)经典方法是最小二乘法

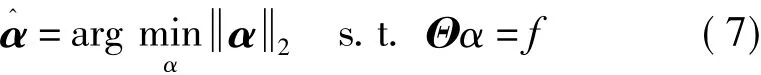
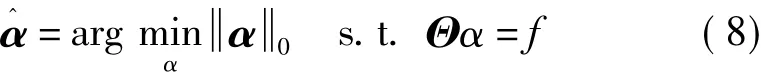
其中，α0表示α中非零元素的个数。这是一个NP难问题。Donoho指出可将l0范数［9］问题转化l1问题

式(9)是一个凸优化的问题。压缩感知的重构过程就是寻求最优的解决凸优化问题的方法，其中基追踪(Basis Pursuit，BP)算法［10］是一种最基本的解决凸优化问题的算法。

目前将重构算法分为贪婪追踪算法、凸松弛算法和组合算法。其中，贪婪追踪算法中的正交匹配追踪(Orthogonal Matching Pursuit，OMP) 算法［11－12］应用最为广泛，下面介绍OMP算法的具体步骤。

输入:观测矩阵Φ，测量值y，稀疏度K。

初始化:残差r0=y，索引集Λ0=∅，t=1。

(1)找出残差r0与观测矩阵Φ的列中内积最大的一列，记录其角标 λ。即

(2)更新索引集 Λt= Λt－1∪{λt}，记录重建原子集合为空矩阵;

(4)更新残差rt=y－，t=t+1。

(5)判断是否满足t＞K，若是则停止迭代;否则，转到步骤(1)继续执行。

从上述OMP算法的步骤可看出，OMP算法是用迭代的方法，每次迭代从观测矩阵Φ中选取与残差最相关的一列作为原子。然后更新残差，并将该列向量从观测矩阵中去掉，将所有迭代得到的原子正交化，再继续进行下一步迭代。如此迭代，直到满足迭代次数或迭代阈值为止。OMP算法在每次迭代时均将得到的原子正交化，这就能保证每次得到的原子与残差均是最相关的，所以OMP算法所需迭代次数较少，故应用较为广泛。

2 观测矩阵的优化

观测矩阵将稀疏信号从高位空间投影到低维空间，在保证信号的重构精度的条件下，要求投影空间维数越低越好。

2．1 矩阵奇异值分解

假设 A∈Rm×n，存在正交矩阵 U∈Rm×m、V∈Rn×n和对角矩阵∑使得

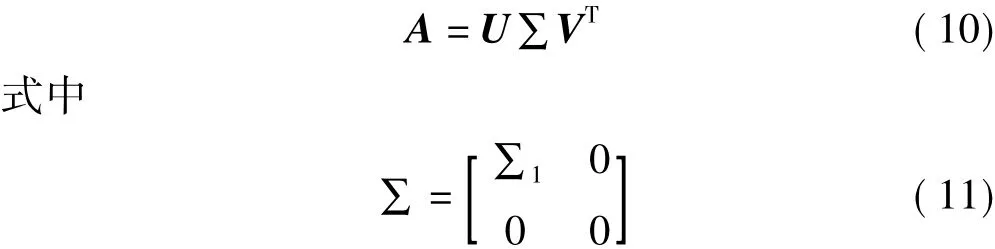
且∑1=diag(δ1，δ2，…，δr)，其对角元素按照顺序 δ1≥δ2≥…≥δr＞0，r=rank(A)排列。这就是矩阵的奇异值分解定理，其中 δi(i=1，2，…，r－ 1，r)为矩阵 A 的奇异值，而式(10)称为矩阵A的奇异值分解。

奇异值具有良好的稳定性、比例不变性、旋转不变性和降维压缩的特性，所以对观测矩阵进行奇异值分解，可较好地反映观测矩阵的性质。

2．2 优化算法

稀疏信号的非零系数集中在低频段，而零系数或近似为零的系数集中在高频段。因此，提高测量矩阵前半段的测量系数，可在采样次数相同的情况下获得更多信号的信息，从而准确重构原始信号。然而增大观测矩阵前半部分系数的必然会降低矩阵的非相干性。由矩阵奇异值分解的性质可知，最大奇异值越小矩阵的非相干性就越好。因此，本文主要工作是设计合理的观测矩阵，提高矩阵的非相干性。实验结果表明，奇异值修正后观测矩阵相对于原矩阵具有更好的RIP性质，重构效果有明显提高。

下面介绍矩阵优化算法的步骤:

(1)生成测量矩阵Φ∈RM×N。

(2)对测量矩阵Φ奇异值分解，求出奇异值，即Φ=U∑VT，其中δr)，(δ1≥δ2≥…≥δr＞0)。

(3)针对信号稀疏表示的观测矩阵的优化。

1)构造一个M×N的全1矩阵H。

2)求出对角矩阵对角线元素的均值ave1，找出大于等于ave1的所有奇异值，记下≥ave1的奇异值的总数j。

3)令矩阵H的前j列乘以加权系数t(t＞1)，得到矩阵H1。

4)将优化矩阵H1与观测矩阵Φ点乘，得到优化的矩阵Φ1。

(5)生成新的观测矩阵Φ2=U1∑'2V1。

3 实验及结果分析

在 CPU 为 Intel T5200(2．00 GHz)，内存为2．00 GB的联想电脑，Matlab7．0的条件下，对随机高斯测量矩阵按照本文的算法进行优化，如图1所示对二维图像做了仿真实验，实验选用的是512×512的Baboon图像，压缩比为0．4，分别采用傅里叶基、离散余弦基和小波基对图像稀疏表示，重构算法采用OMP算法，对比改进前后重构的图像。图2所示为Baboon(512×512)图像在不同压缩比时重构图像的重构精度和时间。经过多次试验证明在t=5时，重构效果较好，故取t=5。

PSNR是最普遍的客观评价图像质量的方法，PSNR值越大重构精度越高，PSNR的计算公式如下

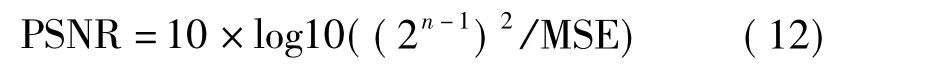
实验结果表明优化算法对傅里叶变换、离散余弦变换、小波变换3种稀疏表示方法都有效果，其中采用傅里叶稀疏表示重构的图像，在观测矩阵优化后，精度增大的幅度最小(1～2 dB)，离散余弦稀疏表示次之，小波变换的精度增大最多，尤其是在压缩比较小时，PSNR可增大8～9 dB，且3种方法经优化矩阵观测重构图像所需的时间虽然增加，但增加量较小，可认为基本相同。

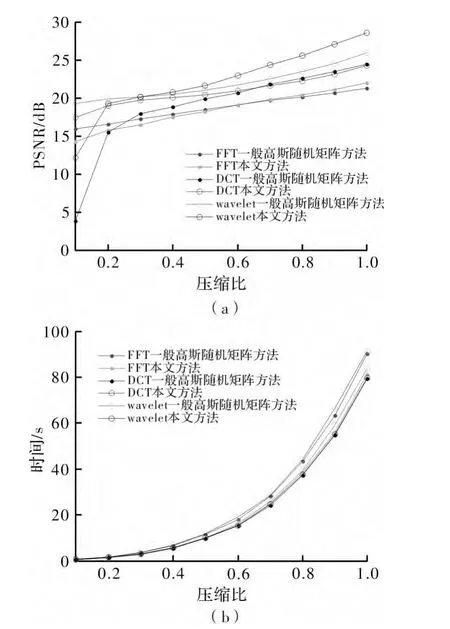
图2 Baboon图像不同压缩比的重构效果图

由以上结论可知，本文的改进算法，不仅适用于大压缩比的情况，且适用于小压缩比的情况，特别的相比传统方法，在小压缩比时的重构效果较好，可大幅提高图像的重构精度，且消耗时间只有小幅增加，可认为与传统方法所用时间相同。

5 结束语

为克服基于压缩感知的图像重构算法存在的不足，结合图像稀疏表示之后再变换域的性质，给观测矩阵赋以权值，并根据矩阵奇异值分解的性质降低矩阵的相干性。根据这一理论对图像进行仿真实验，实验结果表明，改进算法提高了重构图像的重构精度，特别是在小压缩比时，基于小波变换的重构图像的精度大幅提高。

［1］ Baraniuk R．A lecture on compressive sensing［J］．IEEE Signal Processing Magazine，2007，24(4):118 －121．

［2］ Candès E J，Romberg J，Tao T．Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information ［J］．IEEE Transactions on Information Theory，2006，52(2):489 －509．

［3］ Candès E J，Romberg J．Quantitative robust uncertainty principles and optimally sparse decompositions［J］．Foundations of Computational Mathematics，2006，6(2):227 －254．

［4］ Donoho D．Compressed sensing［J］．IEEE Transactions on Information Theory，2006，52(4):1289 －1306．

［5］ Donoho D，Tsaig Y．Extensions of compressed sensing［J］．Signal Processing，2006，86(3):533 －548．

［6］ Emmanuel Candès，Justin Romberg，Terence Tao．Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information［J］．IEEE Transactions on Information Theory，2006，52(2):489 －509．

［7］ Penne E K，Mallat S．Image compression with geometrical［C］．Proceeding of ICIP，2000:661 －664．

［8］ Candès E J，Romberg J．Sparsity and incoherence in compressive sampling ［J］．Inverse Problems，2007，23(3):969－985．

［9］ Fang Hong，Zhang Quanbing，Wei Sui，et al．A method of image reconstruction based on sub－gaussian random projection［J］．Journal of Computer Research and Development，2008，45(8):1402 －1407．

［10］ Scott Shaobing Chen，David L Donoho，Michael A Saunders．Atomic decomposition by basis pursuit［J］．Society for Industrial and Applied Mathematics，2001，43(1):129 －159．

［11］ Tropp J A，Gilbert A C．Signal recovery from random measurements via orthogonal matching pursuit［J］．IEEE Transactions on Information Theory，2007，53(12):4655 －4666．

［12］ Mallat S，Zhang Z．Matching pursuits with time－ frequency dictionaries［J］．IEEE Transactions on Signal Processing，1993，41(12):3397 －3415．