BPSK，QPSK，UQPSK，64QAM信号自动调制识别

于 洋，李孝严，张晓春

(1.西安电子科技大学电子信息攻防对抗与仿真技术教育部重点实验室，陕西西安 710071;2.西安电子科技大学微电子学院，陕西西安 710071;3.中北大学电子测试技术国家重点实验室，山西太原 030051)

随着电子技术和无线通信技术的快速发展，调制识别技术得到广泛的应用，尤其是在军事、民用领域，近年来始终备受关注。为充分利用通信资源，通信信号的体制、调制样式更加多样化和复杂化，调制识别技术在不断发展，并应用于各个领域。通信环境也在不断变化，使得同一空间的信号越发密集，接收到的信号也存在多种不同的调制方式。近年来，随着深空通信技术的不断发展，使得星间链路信号的调制识别具有重要意义。由于数字调相信号自身具有频带利用率高、抗干扰能力强等优点，其被广泛应用于星间链路通信中。随着，传输容量的不断扩大，可用的频带受限，数字调制方式以由二相的BPSK发展为四相的QPSK、UQPSK，既调相又调幅的MQAM信号。所以对数字调相信号的识别就显得尤为重要，特别是在先验知识缺乏，低信噪比条件下的调制类型的自动识别。虽目前学者针对调制类型的识别已做了大量研究，识别技术也已较为成熟，但对于复杂调制信号MPSK、MQAM的自动识别仍是难点。

目前，实现通信信号的调制识别研究越来越多，主要有利用四阶累积量实现了BPSK与QPSK信号的分类［1］;利用四阶累积量实现 BPSK，QPSK，8PSK 信号的分类，并证明高阶累积量对信号星座图的平移、尺度和相位旋转等变换具有不变性［2］;利用二阶、四阶、六阶累积量实现 2ASK，4ASK，QPSK，2FSK，4FSK 信号的分类［3］;Mammonf通过记录下码元时刻的相位变化来进行调制类型分类［4］;Soliman和Hsue采用相位的n阶矩识别MPSK信号［5］;Polydoros和Kim则开发出一种针对BPSK和QPSK分类的近似似然率调制分类器;利用基于云模型的方法将调制信号的幅度、相位等特征映射到数域空间完成对QPSK和QAM的识别［6］;利用相位差分的脉内调制识别方法完成QPSK和BPSK的识别［7］;利用基于信号二倍频谱、四倍频谱特性分析调制识别算法，对 BPSK、QPSK、OQPSK信号进行识别初探［8］。上述文献中有些存在计算量较大，需要的先验知识多、无法对UQPSK信号进行有效识别等不足。

在文献［1，3］的基础上，主要针对星间链路通信中常用的MPSK和MQAM调制类型中的BPSK、QPSK、UQPSK、64QAM调制信号，采用改进的提取特征参数高阶累积量的方法进行通信调制类型的自动识别。

1 4种信号的模型分析

1.1 BPSK信号模型

BPSK的信号模型为

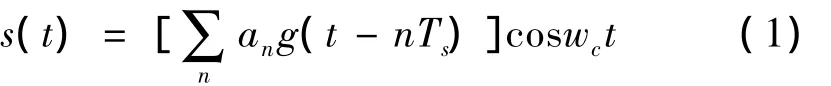
1.2 QPSK信号模型

QPSK的信号模型为

从式(2)可看出，QPSK即两路正交的BPSK的叠加。

1.3 UQPSK 信号模型

UQPSK信号即非平衡的QPSK信号，属于QPSK信号，不同在于UQPSK的两路正交BPSK幅度不相等，其信号模型为

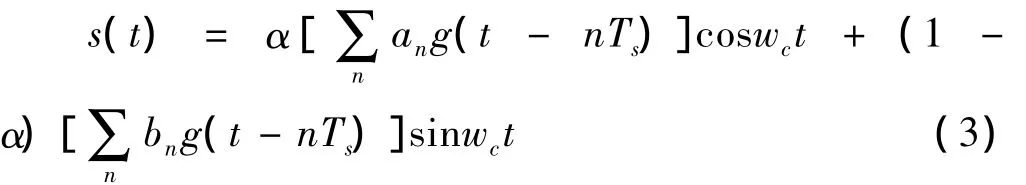
其中，α为平衡因子，代表正交两路的幅度。当平衡因子α为0或1时，UQPSK即为BPSK信号;当平衡因子α为0.5时，UQPSK信号即为QPSK信号。

1.4 64QAM信号模型

64QAM信号，即64正交幅度调制信号，相比于前3种相位调制而言，又增加了幅度的调制，其信号模型为

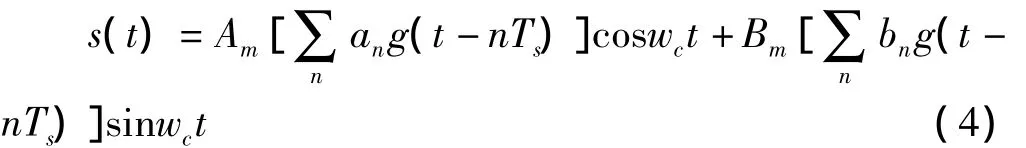
其中，Am={1，3，5，7}，Bm={1，3，5，7}，Am，Bm共 64种组合，64QAM由此而来。

2 高阶累积量的理论分析

由于高斯随机过程的高阶累积量恒为零，所以非高斯信号在与之独立的加性高斯噪声中被观测的话，则观测过程的高阶累积量将与非高斯信号过程的高阶累积量恒等。因而使用高阶累积量作为分析工具，理论上可完全抑制高斯噪声的影响，所以高阶累积量是高斯噪声背景下提取非高斯信号的有效工具，亦是研究信号识别的重要理论基础。对于复平稳信号x(t)，其高阶矩表示为

式中，X为接收的复平稳信号;X*为X的共轭。

常用的高阶累积量表示为

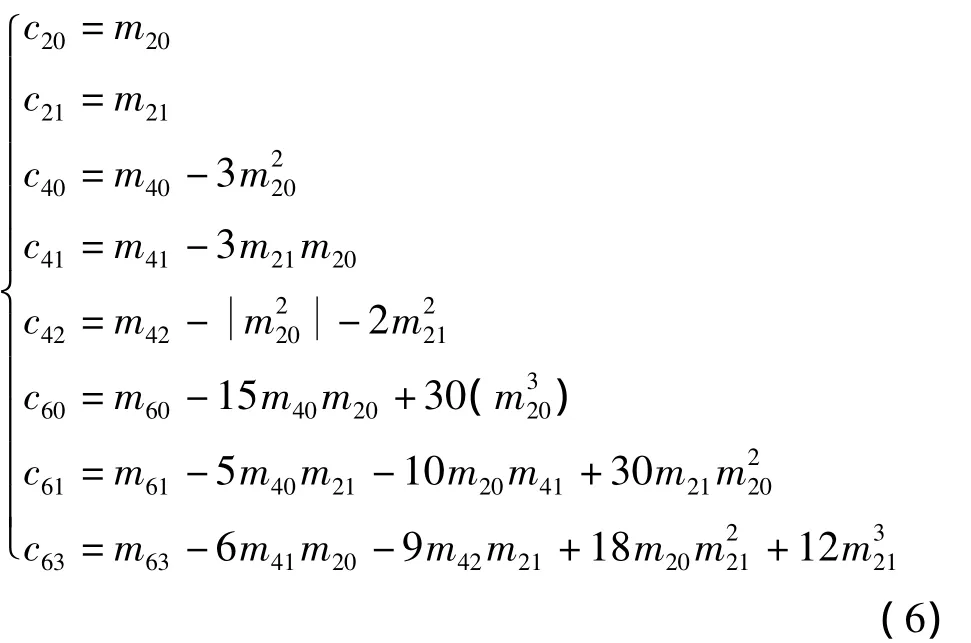
式中，c20、c21、c40、c41、c42、c60、c61、c63分别为二阶、四阶、六阶累积量，由于高斯过程的奇数阶矩为零，偶数阶矩不为零，其高阶累积量(k≥3)恒等于零，这就是高阶累积量处理信号可以去噪的原因［9］。

通信信号识别特征参数提取BPSK、QPSK、UQPSK和64QAM这4种调制信号的高阶累积量理论值，如表 1［10］所示。

表1 4种调制信号的高阶累积量的理论值

其中，E为信号的能量，为实现数字调制信号的调制分类，可利用不同阶累积量的组合建立识别参数，文中主要采用四、六阶累积量建立识别参数。通过观察表1，为避免噪声和接收信号的功率对识别的影响，构建如下分类特征统计量

由此可知，对于BPSK、UQPSK而言，理论值Fx1=1，而 QPSK、64QAM 的 Fx1=0，Fx1能较好地将 BPSK、UQPSK和QPSK、64QAM区分;BPSK的理论值Fx2=32，UQPSK 的 Fx2=26，所以 Fx2能将 BPSK 和 UQPSK区分开来;QPSK的理论值Fx3=16，64QAM的Fx3=13.5，故Fx3能将QPSK和64QAM区分开来。总设计识别流程，如图1所示。

图1 调制类型识别流程图

图 1 中的 Thr1、Thr2、Thr3为设定的门限值，Thr1用来区分 BPSK、UQPSK与 QPSK、64QAM;Thr2用来区分64QAM和 PQSK;Thr3用来区分 BPSK和 UQPSK，Thr1，Thr2，Thr3门限的选择在不同信噪比下进行100次蒙特卡洛试验获得。

3 算法的仿真结果与性能分析

为分析算法的性能及信噪比对识别性能的影响，通过Matlab仿真实验来评估改进算法的性能。仿真参数选取为:码元速率 2 Mbit·s－1，载波频率为 105 MHz，采样频率为60 MHz，码元个数为200，信噪比SNR选取范围－5～25 dB，对4种信号分别进行100次蒙特卡洛实验，其中UQPSK的非平衡因子选取0.25，仿真结果如图2～图5所示。

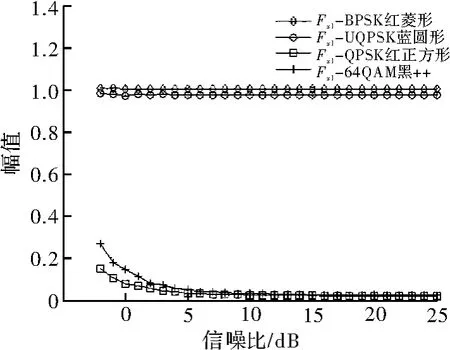
图2 特征参数Fx1的仿真图

图3 特征参数Fx2的仿真图

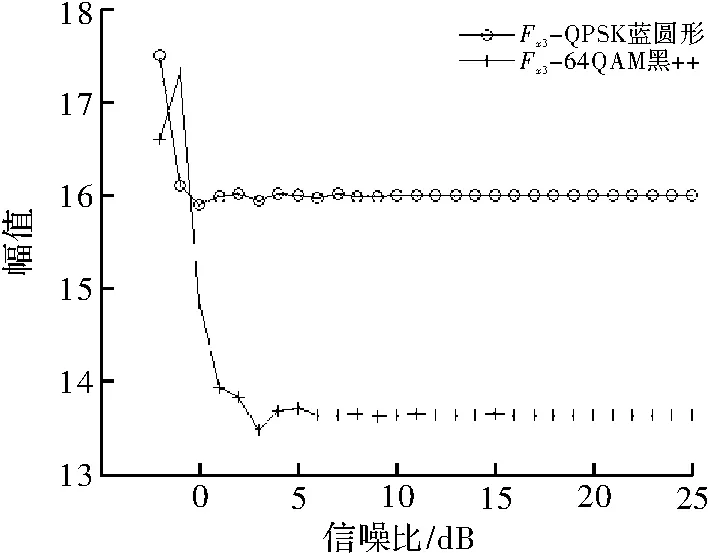
图4 特征参数Fx3的仿真图

图5 识别率随SNR变化的仿真图

此调制类型自动识别算法的关键在于Thr1、Thr2、Thr3这3个门限的确定。通过上图可看出，在NSR≥0 dB时，该方法具有较好的适应性，能够较好地区分出BPSK、QPSK、UQPSK、64QAM 这 4种调制信号。如图2～图4所示，Thr1门限值的选取在［0.6，0.8］之间效果最佳，Thr2门限值的选取在［29，31］之间效果最佳，Thr3门限值的选取在［14.5，15.5］之间效果最好。门限选取的准确与否直接影响到信号识别的准确性，如图3～图4所示，Fx2和Fx3在0～5 dB之间会有跳变点，若门限过高或过低，会造成64QAM和PQSK、BPSK和UQPSK的误判，使信号的识别率下降。上述门限是对100次蒙特卡洛仿真结果进行平均得到的理想门限值，图5是验证信噪比对调制类型识别率的影响。选取 Thr1=0.7，Thr2=30.5，Thr3=15，从图中可看出，在SNR=0 dB时，4种信号的识别率约为60%，随着信噪比的逐渐增加，识别率不断提高;当SNR≥5 dB时，BPSK、QPSK、64QAM的识别率≥95%，UQPSK识别率≥90%;当SNR≥10 dB时，4种调制类型的识别率接近100%，识别率较好。

4 结束语

在基于高阶累计量算法的基础上，提出了用于调制类型识别的新特征参数，通过理论分析和仿真实验，其结果表明在一定的信噪比条件下能较好的对星间链路中常用的BPSK、QPSK、UQPSK、64QAM调制类型进行自动识别，且运算量小、实时性好，适合工程应用。但由于UQPSK的非平衡因子的取值不同，使得其有时与BPSK、QPSK性质相类似，容易造成混淆，所以对UQPSK的识别将是今后研究的重点。

［1］Swami A，Sadler B M.Hierarchical digital modulation classification using cumulates［J］.IEEE Transactions on Communications，2010，48(3):416 －429.

［2］陈卫东，杨绍全.利用累量不变量对MPSK信号分类［J］.西安电子科技大学学报，2008，29(2):229－232.

［3］吕新正，魏平.利用高阶累积量实现数字调制信号的自动识别［J］.电子对抗技术，2004，19(6):3 －6.

［4］Mammonf R J，Rpthaker.Estimation of carrier frequency，modulation type and bit rate of an unknown modulated signal［C］.Proceedings of ICC'87，1987:1006 －1012.

［5］Hsue S Z，Soliman S S.Automatic modulation classification using zero crossing［J］.IEEE Proceeding，1990，137(3):459－464.

［6］吕燕，唐斌.基于模糊分类的调制信号自动识别方法［J］.电子对抗技术，2005，20(4):19 －22.

［7］李兴生，杜蔚轩，李德毅.基于云模型PSK/QAU信号调制识别方法［J］.测控技术，2013，22(3):15 －19.

［8］黄知涛，周一宇.一种有效的BPSK/QPSK信号调制识别方法［J］.电子对抗技术，2005，20(2):10 －13.

［9］冯小平，李鹏，杨绍全.通信对抗原理［M］.西安:西安电子科技大学出版社，2009.

［10］李晏.基带 PSK、QAM信号调制子类型自动识别研究［D］.成都:电子科技大学，2008.