辐射源载频对测向定位的影响

刘 洋

(西安电子科技大学电子工程学院，陕西西安 710071)

无源定位系统最大的优点在于工作时自身不发射电磁能量，所以具有良好的隐蔽性，能有效抵抗反辐射导弹和反侦察定位系统，因此生命力强，适应环境快［1］。测向交叉定位技术由于成本低，定位方程为线性方程，且具有一定的抗干扰能力，所以成为了无源定位系统中相对成熟，应用较广的方法。文献［2］中对定位算法进行了研究;文献［3］中分析了测向交叉定位的原理、测角精度、基线长度以及辐射源与接收站的相对位置对定位的影响［3］。上述文献中仅研究了无源探测系统本身，以及算法对定位性能的影响，并未建立起辐射源特征与定位性能的关系。因此，本文针对测向定位中辐射源载频对定位性能的影响，建立了辐射源载频与定位精度的定量关系，对不同载频下的定位精度进行了仿真分析。

1 定位基本原理

测向法定位是在已知的两个或多个不同位置上测量辐射源电磁波到达方向，然后利用三角几何关系计算出辐射源位置，因此又被称为三角定位法。三维测向定位模型，如图1所示。

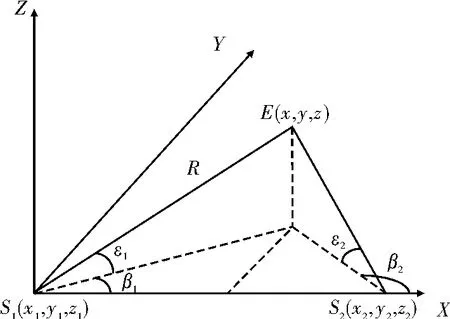
图1 测向定位基本原理图

图1中，S1，S2为两个观测站;E为目标辐射源;β1，ε1为观测站 S1测量到的方位角与俯仰角;β2，ε2为观测站S2测量到的方位角与俯仰角［4］。

根据三角关系，有

根据式(1)解出辐射源E(x，yz)即实现了定位。具体过程可通过 β1，β2，ε1，ε2中的 3 或 4 个变量来求解，下面以β1，β2，ε1求解辐射源位置为例，解得辐射源与观测站1的距离为

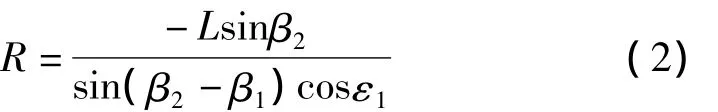
利用R即可求得辐射源位置

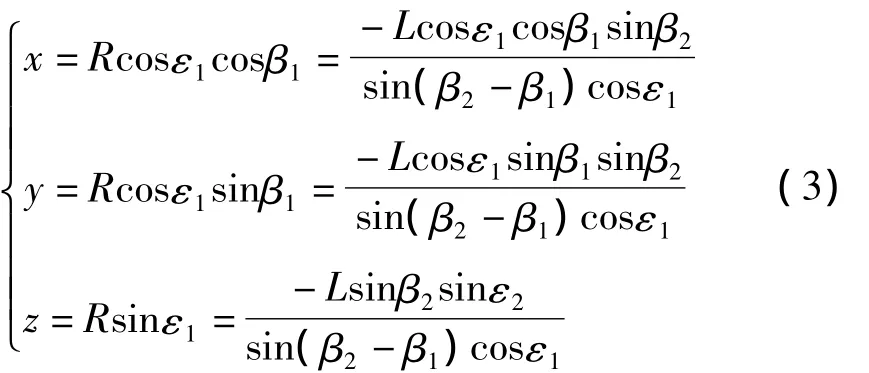
2 定位误差分析

假设各测量误差均为零均值，且彼此不相关的高斯白噪声。方位角、俯仰角的测量误差标准差分别为σβ，σE站址各分量的测量误差以及与其他测量误差之间均相互独立，具有相同的标准差σs。

在不考虑布站误差的情况下，以 β1，β2，ε1求解辐射源位置为例，对其定位误差进行分析。

写成矩阵形式［5］

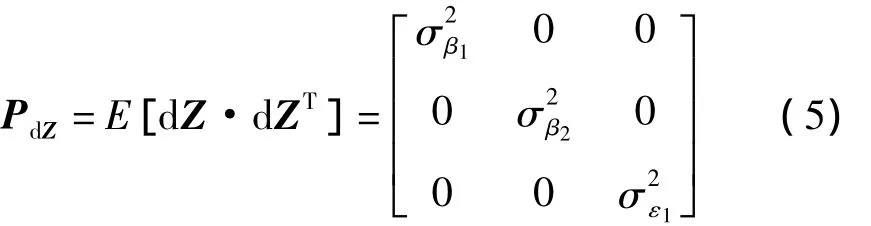
定位误差协方差矩阵为

以辐射源雷达为例，假设雷达与侦查接收机的距离为R，则接收机内部信噪比为

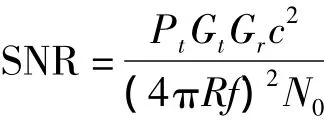
其中，Pt为雷达发射功率;Gt为雷达天线增益;Gr为接收机天线增益;c为光速;f为辐射源载频;N0为接收机内噪声［7］。

3 仿真结果分析

仿真条件1 测向体制选用比幅法测向，辐射源发射功率Pt为50 kW;发射天线增益Gt为20 dB，侦查接收机天线增益 Gr为15 dB;接收机带宽 B=3 GHz;玻尔兹曼常数 k=1.38 ×10－23，T0=290 K;噪声系数Fn=6 dB;半功率波束宽度θr为30 dB;辐射源载频f为10～19 GHz;主站位置 S1(－50，0，0)km，S2(50，0，0)km辐射源取基线中垂线方向上，高度为50 km的一系列点，即辐射源目标的x坐标为0 km，z坐标为50 km。

定位精度与载频及目标位置关系，如图2所示，定位精度与目标辐射源的载频以及位置的关系。由图中可知，当目标辐射源的位置不变时，辐射源载频越大、定位误差越大，当目标辐射源的载频不变时，目标辐射源与观测站的距离越远，定位误差越大、载频越大，定位误差随着距离的变化越快，与理论分析相符。

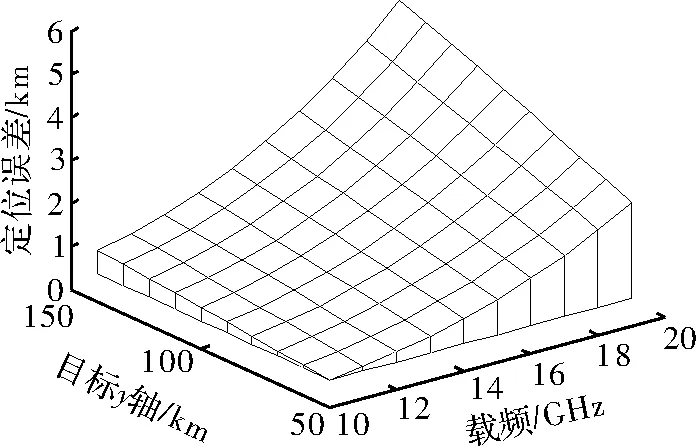
图2 比幅法测向时定位误差与载频及目标位置关系图

仿真条件2 测向体制选用干涉仪法测向，测相位误差Δφ=20°，测频误差Δf=100 MHz;干涉仪基线长度d=30 cm;辐射源载频f为10～19 GHz;主站位置S1(－50，0，0)km，S2(50，0，0)km;辐射源取基线中垂线方向上，高度为50 km的一系列点，即辐射源目标的x坐标为0 km，z坐标为50 km。

定位精度与载频及目标位置关系如图3所示，定位精度与目标辐射源的载频以及位置的关系。由图中可知，当目标辐射源的位置不变时，辐射源载频越大，定位误差越大，当目标辐射源的载频不变时，目标辐射源与观测站的距离越远，定位误差越大，载频越大，定位误差随着距离的变化越快，与理论分析相符。

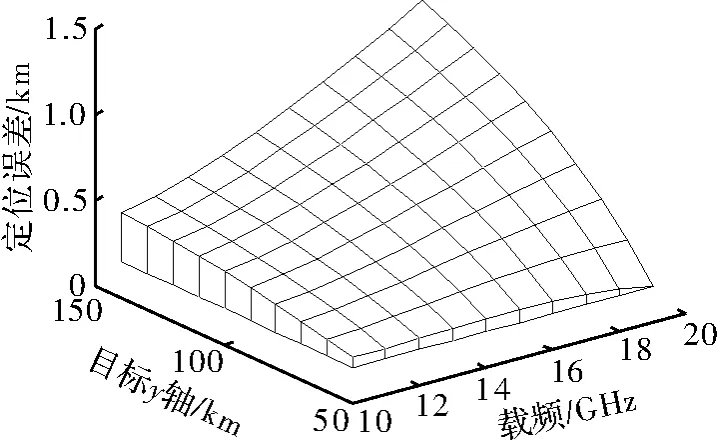
图3 干涉仪法测向时定位误差与载频及目标位置关系图

4 结束语

采用测向方法定位时，主要影响定位误差的因素有测角精度以及辐射源与观测站的相对位置。无论使用比幅法测向还是干涉仪测向，辐射源载频均会影响测角精度，辐射源载频越大，测角精度越低，定位误差越大，且辐射源载频越大时，定位误差随着辐射源与观测站的距离的变化越快。作为被侦察方，可以通过提高自身载频使侦察方定位误差变大，进而造成无法精确定位，具有一定的实际应用意义。

［1］赵国庆.雷达对抗原理［M］.西安:西安电子科技大学出版社，2009.

［2］罗争.基于径向基神经网络的空间目标测向定位算法［J］.探测与控制学报，2011(6):29 －33.

［3］汪珺.测向交叉定位技术［J］.电子科技，2011，24(7):129－132.

［4］汤扣林.三维空间测向定位技术［J］.火力与控制指挥，2011(5):111－117.

［5］张宛怡.无源测向与时差定位技术研究［D］.成都:电子科技大学，2013.

［6］苟艳妮，王英民，王奇.一种修正的浮标用多波束比幅法测向精度研究［J］.电声技术，2013(2):49－53.

［7］李鹏，武胜波.比幅法测向及其误差分析［J］.技术平台，2009(10):89－92.

［8］田德民.影响干涉仪测向接收机测向精度的因素分析［J］.舰船电子对抗，2010(4):46－48.