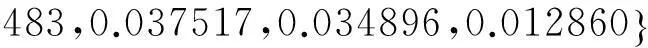基于时间最优的费诺编码算法研究与设计
2015-12-17王防修刘春红
王防修,刘春红
(1.武汉轻工大学 数学与计算机学院,湖北 武汉 430023,2.鄂钢驰久钢板弹簧有限责任公司,湖北 鄂州 436000)
基于时间最优的费诺编码算法研究与设计
王防修1,刘春红2
(1.武汉轻工大学 数学与计算机学院,湖北 武汉 430023,2.鄂钢驰久钢板弹簧有限责任公司,湖北 鄂州 436000)
摘要:针对费诺编码的算法研究与实现问题,提出一种最优偏差值与分治法相结合的算法。算法以最小偏差值为目标,在概率序列中寻找最佳断开位置,通过最佳断开位置实现费诺编码。鉴于费诺编码算法的递归属性,分别设计了编码的多模块算法和单模块算法。通过对算法时间复杂度的分析,对设计的算法进行了改进。算例仿真表明,不同算法对同一信源编码所耗费的时间差异很大,选择时间最优的费诺编码算法能更好地满足费诺编码系统对适时性的要求。
关键词:时间最优;多模块算法;单模块算法;最优偏差值;分治法
1引言
在三大经典变长编码[1]中,哈夫曼编码的编码效率最高,香农编码的编码效率最低,而费诺编码的编码效率处于两者之间.在特殊情况下,三者编码效率相同.然而,只有香农编码[2,3]]和哈夫曼编码[4-8]被广泛研究和应用,而费诺编码的算法原理及实现尚未见之于文献。虽然文献[1]给出了费诺编码的思想和几个具体的例子,但费诺编码的原理并没有给出.本文针对费诺编码的算法实现问题,提出了用分治法进行费诺编码的算法思想,设计了几种不同的算法来实现费诺编码。通过对不同算法对同一信源编码所花费的时间进行算法比较,从中得出时间最优的费诺编码算法。
2用分治法实现费诺编码的基本原理
所谓用分治法进行费诺编码,就是是将一个规模为n的问题分解为两个规模较小的子问题,这两个子问题相互独立与原问题相同。递归地解这些子问题,然后将各子问题的解合并就可以得到原问题的解。
给定包含n个事件的单信源X={x1,x2,…,xn},设事件xi对应的概率为pi(i=1,2,…,n),且概率pi满足下述三个条件:
p1≥p2≥…≥pn;
(1)
0 (2) (3) 根据费诺编码的原理,将满足上述条件的概率序列pipi+1…pj断开为两个子序列pipi+1…pk和pk+1pk+2…pj,然后对这两个子序列对应的各事件分别进行0和1编码,递归地对子序列重复该过程,直到每个子序列的长度都为1,就可以得到每个事件的编码。因此,费诺编码的关键是确定序列pipi+1…pj的断开位置k。 设m(i,j)表示从pi至pj这j-i+1个概率的和,其中1≤i≤j≤n。则: 当i=j时,有m(i,i)=pi. (4) (5) 或 m(i,j)=m(i,j-1)+m(j,j). (6) 如果用(5)求出所有的m(i,j),其中1≤i (7) 然而,如果用(6)求所有的m(i,j),1≤i (8) 设pi>pi+1>…>pj和i≤k (9) (10) 如果用s(i,j)表示将概率序列pipi+1…pj断开为两个概率子序列的断开位置,则根据费诺编码的原理,其断开位置s(i,j)必须满足下列关系: s(i,i)=i,i=1,2,…,n. (11) s(i,j)=k,1≤i (12) 其中k满足 (13) 这样,从概率序列pipi+1…pj的位置k将该序列断开为两个子序列pipi+1…pk和pk+1pk+2…pj。用递归的方法,将pipi+1…pk和pk+1pk+2…pj进一步断开,直到i=j为止。 如果用d(i,j)表示pipi+1…pk和pk+1pk+2…pj的最优偏差值,即 (14) 其中k=s(i,j),则有: 因此,只要知道概率序列pipi+1…pj的断开位置s(i,j),就可以立即求出最优偏差值 (16) 设事件序列xixi+1…xj对应的编码为bibi+1…bj,则未进行编码之前,事件xk的编码初始化为 bk=φ,k=i,i+1,…,j. (17) 求出s(i,j)后,对事件xk进行编码的过程如下: bk=bkØ,k=i,i+1,s(i,j). (18) 和 bk=bk1,k=s(i,j)+1,…,j. (19) 求出s(i,s(i,j))后,对xixi+1…xs(i,j) 中的事件进行递归编码。 同理,xs(i,j)+1…xj中的事件是根据s(s(i,j)+1,j)断开进行递归编码的。 信源X={x1,x2,…,xn}的熵为 (20) 其中0 (21) 因此,费诺编码的编码效率 (22) 3算法设计 设递归函数f(i,j)是对事件序列xixi+1…xj的费诺编码,则通过执行f(i,j)可以对事件序列x1x2…xn中每个事件xi(i=1,2,…,n)编码。 下面算法的步骤1到步骤3中每个步骤对应一个功能模块,步骤4是编码模块。 步骤1 通过(4)和(6)计算m(i,j),1≤i 步骤2 通过(11),(12)和(13)计算s(i,j);根据(16)计算d(i,j)。具体过程如下: a.令s(i,i)=i和d(i,i)=0,i=1,2,…,n. b.初始化r=1和i=1. c.使j=i+1和s(i,j)=i. d.由(13)求出s(i,j)和(16)求出d(i,j). e.如果i f.如果r 步骤3递归函数f(i,j)编码的过程如下: a.如果i=j,则编码结束。 b.bk=bk0,k=i,i+1,s(i,j). c.bk=bk1,k=s(i,j)+1,…,j. d.分别调用f(i,s(i,j))和f(is(i,j)+1,j). 步骤4 通过调用f(1,n)实现递归编码,最后得到每个事件xi的编码bi,i=1,…,n. 在算法3.1的步骤2所对应的模块中,求d(i,j)和s(i,j)的时间复杂度为O(n3)。如果能对该模块加以改进,则可以大大减少编码时间。设改进后的模块为递归函数g(i,j),则该函数的递归过程如下: a.如果i=j,则递归过程结束; c.使s(i,j)=k和d(i,j)= d.递归调用g(i,k)和g(k+1,j). 最后,通过调用递归函数g(1,n)就可以求出编码过程需中需要的全部断开位置。 算法3.1和算法3.2都是自顶向下的多模块设计,算法中的模块执行顺序不能改变。其优点是算法的数学模型简单,缺点是计算m(i,j)时需要花费更多的机时。为此,下面编码算法是用单一递归模块h(i,j)进行设计的: a. 如果i=j,则递归过程结束。 d.初始化k=i+1. e.使tl=tl+pk和tr=tr-pk. g.如果k h.bk=bk0,k=i,i+1,s(i,j)和bk=bk1,k=s(i,j)+1,…,j. i.递归调用h(i,s(i,j))和h(s(i,j)+1,j). 因此,最后只要调用h(1,n)就可完成所有信源事件的编码。 4算法仿真 本算法使用VC6.0作为仿真工具,在CPU为3.2GHz和内存为1.86GB的个人台式电脑上完成仿真。本节将对费诺编码的几种不同算法设计进行实例比较。 解首先,求得最优偏差值: d(1,11)=0.060 956,d(1,2)=0.100 574 d(3,11)=0.007 982,d(3,5)=0.063 164 d(4,5)=0.001 310,d(6,11)=0.015 718 d(6,7)=0.001 488,d(8,11)=0.022 036 d(8,9)=0.003 966,d(10,11)=0.003 966 和最优断开位置: s(1,11)=2,s(1,2)=1,s(3,11)=5 s(3,5)=4,s(4,5)=4,s(6,11)=7 s(6,7)=6,s(8,11)=2, s(8,9)=8,s(10,11)=10. 根据断开位置得到的编码如表1所示。 表1 11个符号的费诺编码 根据(20),信源熵H(X)=3.045 056 (bit/符号)。 根据(21),经过费诺编码后的平均码长 根据(22),编码效率为η=0.98587 923. 虽然分别用算法3.1,算法3.2和算法3.3对算例进行编码,会得到相同的编码结果,但所花费的时间是不同的。实验表明,它们所花费的时间分别为:0.006 2ms, 0.003 1ms,0.001 5ms. 从编码所花费的时间看,算法3.3花费的时间最少,算法3.2次之,算法3.1用时最多,这种结果与算法设计的原理是一致的。然而,单从一个算例还无法说明算法3.3在编码时间上就一定是最优的。为了进一步比较这三种算法在编码时间方面的优劣,在此随机选取10个不同单信源进行测试,实验结果如表2所示。其中,表中的T1,T2和T3分别表示三种算法的编码时间。 5算法分析 从表1显示的实验数据可以看出: 1)笔者设计的三种算法对同一信源编码所耗费的时间差别很大; 表2 不同费诺编码算法的实验结果统计 2)三种算法的编码时间均随信源符号的个数增大而增大; 3)伴随信源符号个数的增加,算法3.1的编码时间提高很快,而算法3.3的编码时间增速缓慢。 算法3.2和算法3.3之所以编码时间比算法3.1要优,是因为前者计算d(i,j)和s(i,j)的时间复杂度为O(n),而后者时间复杂度为O(n3)。同样,算法3.3的编码时间之所以明显优于算法3.2,是因为算法3.3计算m(i,j)的时间复杂度为O(n),而算法3.1和算法3.2计算m(i,j)的时间复杂度为O(n3)。 6结束语 本文提出了一种基于时间最优的快速费诺编码算法。该算法使用了最优偏差值与分治法相结合的方法来对信源符号编码,该算法缩小了概率序列位置断开的计算量,减少了递归过程中一些变量的重复计算,提高了信源符号的编码速度。从算法仿真可以看出,虽然费诺编码的原理是相同的,但不同的费诺编码算法设计所产生的编码速度完全不一样。因此,在实际编码过程中,编码速度快的算法自然更加受到青睐。在上面介绍的三种算法中,由于算法3.3的时间最优,故对一个费诺编码系统而言,算法3.3更能满足该编码系统对适时性的要求。 参考文献: [1]叶芝慧,沈克勤.信息论与编码[M].北京:电子工业出版社 ,2013. [2]邵军花 ,刘玉红.香农编码的优化算法研究[j].兰州交通大学学报,2010,12,29(6):110-113 [3]谢勰.关于Shannon编码的若干注记[J].西安邮电学院学报, 2009,5,14(3):58-60. [4]王向鸿.基于Matlab文本文件哈夫曼编解码仿真[J] 现代电子技术, 2013,10,36(20):31-32. [5]薛向阳. 基于哈夫曼编码的文本文件压缩分析与研究[J]. 科学技术与工程, 2010,8,10(23):5779-5781. [6]程佳佳,熊志斌.哈夫曼算法在数据压缩中的应用[J] 科学技术与工程, 2010,2:35-37. [7]阚君满.基于改进哈夫曼编码的全文索引结构压缩算法[J] 吉林大学学报, 2011,9,29(5):473-476. [8]邓宏贵,郭晟伟,李志坚.基于哈夫曼编码的矢量量化图像压缩算法[J] 计算机工程, 2010,4,36(4):218-222. Fano Coding algorithm research and design based on time optimal matching WANGFang-xiu1,LIUChun-hong2 (1.School of Mathematics and Computer Science,Wuhan Polylethnic University,Wuhan 430023,China; 2. Ezhou Iron and Steel Plate Spring Co Ltd, Ezhou 436000,China) Abstract:According to the algorithm Research and implementation problems of Fano coding, this paper presents an algorithm with optimal deviation Combined with divide and conquer。In order to gain optimal deviation value, the algorithm must find the best open position in the probability series and achieve fano coding by the position. Given the recursive property in Fano coding algorithm, coding algorithm is designed for multi-module and single-module algorithm. By the time complexity analysis of the algorithm , the algorithm is improved. Examples simulation results show,difference in time-consuming is very large for different algorithms to encode the same information source,and Choose the best time Fano coding algorithm can better meet the requirements for timeliness for the coding system. Key words:time optimal;multi-module algorithm;single module algorithm;optimal deviation;divide and conquer 中图分类号:TP 391 文献标识码:A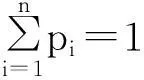
2.1 递归子结构


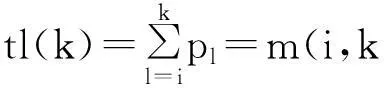



2.2 计算最优值



2.3 构造最优解
2.4 计算编码效率



3.1 模块化设计
3.2 位置递归函数的算法改进


3.3 单模块设计