微胶囊相变悬浮液管内层流换热理论研究
2015-12-16朱换换
朱换换,李 芃
(同济大学机械与能源工程学院,上海201804)
微胶囊相变悬浮液管内层流换热理论研究
朱换换,李芃
(同济大学机械与能源工程学院,上海201804)
基于Fluent软件,对定热流圆管内微胶囊相变悬浮液层流强化换热进行数值模拟。用修正换热系数比γ分析其换热影响因素。结果表明,体积浓度是主要影响因素,γ随其增加而变大,可大于2,管壁温可降低约25%。雷诺数和颗粒直径的增大,热流密度、相变温度区间和过冷度的减小都有利于其强化换热。最后提出一个热-动力性能比ε来综合评价微胶囊相变悬浮液的换热和流动性能。模拟结果对微胶囊相变悬浮液的进一步研究奠定基础。
微胶囊相变悬浮液;层流;强化换热;理论研究
0 引言
微胶囊相变悬浮液是将微胶囊化的相变材料(1~1000μm),添加到一定的载流体(如水等)中所形成的固液混合液。微胶囊相变材料使相变材料与载流体相分离,因而在悬浮液中可以避免相变材料的沉淀和聚集[1,2]。它具有储存/输送热量和强化传热的双重功能,但又可保持很好的流动性[1]。它在各领域(如建筑暖通空调、电力系统、余热利用、太阳能利用等)的换热设备具有广阔的应用前景和潜在利用价值[1~5]。
自20世纪80年代以来,国内外很多学者已经展开对微胶囊相变悬浮液的制备、流动和传热性能的理论、数值模拟和实验研究,并取得了很多突破性的进展。例如,Charunyaorn等[6]通过含有内热源项的层流流动能量控制方程对定热流圆管内微胶囊相变悬浮液的层流流动进行数值模拟。结果表明,悬浮液的努赛尔数Nu比水可提高2~4倍。斯蒂芬(Stefan)数和微胶囊颗粒体积浓度(c)是最主要的影响因素。Goel等[8]实验研究表明,与单相流体相比,悬浮液作为传热流体可使管道壁温降低50%。Stefan数是最主要的影响因素,而微胶囊颗粒体积浓度对其换热的影响并不显著。增大颗粒直径有利于悬浮液的换热。Roy和Avanic等[11~3]的研究也认为体积浓度对悬浮液总体换热影响不大,雷诺数在传热过程中不是一个独立参数。张寅平等[15]提出的内热源模型克服了等效比热模型的不足,给出模拟微胶囊相变悬浮液换热性能的一个新思路。结果认为,Stefan数和体积浓度是最主要的影响因素,但过冷度、相变温度区间、颗粒直径等也是影响换热性能的因素。其他研究文献[1][7][17~19]也表明微胶囊相变悬浮液换热强化的主要影响因素是Stefan数、体积浓度和相变潜热值,但微胶囊相变颗粒直径、相变温度区间、过冷度等也是不可忽视的影响因素。
虽然微胶囊相变悬浮液具有很大优势,但目前应用实例非常少。这是由于研究过程中还存在很多问题,如稳定性和过冷现象等问题[20],使其应用受到限制。已有数值模拟文献[12~14]中,大多是根据建立的数值模型,对方程组进行编程求解,过程相对复杂,工作量较大。Fluent软件在流体流动和热交换方面的问题模拟已较为成熟和普遍,不仅满足精度要求,而且工作量大大简化,同时还可形象生动地观察流体流动情况。因此,本文利用Fluent软件对微胶囊相变悬浮液定热流条件下管内层流流动和换热情况进行模拟,提出微胶囊相变悬浮液修正换热系数比γ来分析各影响因素。同时,还定义了微胶囊相变悬浮液的热-动力性能比ε来对其换热和流动进行一个综合评价。
1 强化换热的无量纲量
1.1修正努赛尔数Nu*和修正换热系数h*
微胶囊相变悬浮液在内部流动时的换热速率受温差的影响。由于流体等效比热容在相变温度段表现出强烈的非线性,甚至出现Nu减小而换热强化的情况[15]。所以,张寅平[15]等重新定义修正努赛尔数Nu*和修正换热系数h*(见公式(2)和(3))。内部流动的传统努赛尔数Nu的定义:

式中h—管内流体的对流换热系数,W/(m2·K);
kf—流体导热系数,W/(m·K);
d—当量直径,m;
q″w—壁面加热热流密度,W/m2;
Tw—管道内壁壁温,K;
Tm—管内流体平均温度,K。
修正努赛尔数Nu*和修正换热系数h*的定义:
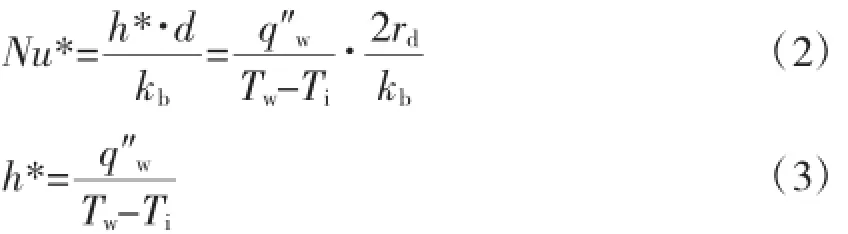
式中h*—微胶囊相变悬浮液的修正换热系数,W/(m2·K);
kb—微胶囊相变悬浮液的整体静态导热系数,W/(m·K);
rd—当量半径,m;
Ti—微胶囊相变悬浮液进口温度,K。
1.2斯蒂芬(Stefan)数
Stefan是微胶囊相变悬浮液显热和潜热之比的无量纲量。在定热流边界条件下,常用的Stefan数定义式见式(4)[1~19]。但从中看出不能显示传热过程中的显热,因为不是流体温度的变化值。因此,根据Ste的物理意义,陈斌娇等[21]提出Ste数的新定义,如式(5)。
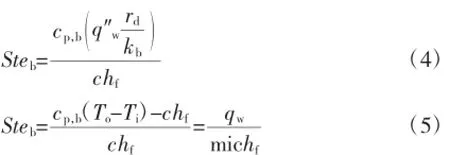
式中Steb—微胶囊相变悬浮液的斯蒂芬(Stefan)数;
cp,b—微胶囊相变悬浮液的整体比热容,kJ/(kg·K);
qw—壁面加热热流量,W;
hf—微胶囊相变材料的相变潜热值,J/kg;
c—微胶囊相变悬浮液的体积浓度;
To—微胶囊相变悬浮液出口温度,K。
1.3修正换热系数比γ
为了表征微胶囊相变悬浮液强化换热的特性,有学者[12]定义了修正强化比η来表示,即微胶囊相变悬浮液与单相流体的修正努塞尔数Nu*之比。但真正表征流体对流换热的参数应该是换热系数h,由式(2)知,修正努赛尔数Nu*中除了修正换热系数h*外,还有流体导热系数等参数。假设悬浮液的Nu比水大,并不能说明其对流换热系数大于水。因此,提出了修正换热系数比γ,即微胶囊相变悬浮液与单相流体的局部修正换热系数之比,见式(6):

式中γ—微胶囊相变悬浮液的修正换热系数比;
2 微胶囊相变悬浮液强化换热机理
微胶囊相变悬浮液无内热源二维圆管内层流流动的能量守恒方程式如下:
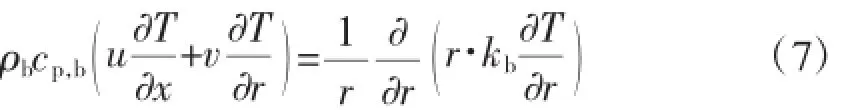
对方程(7)在管内热边界层δt内积分得:
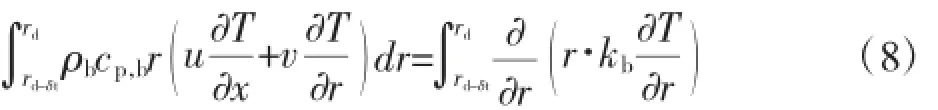
定义无量纲参数:
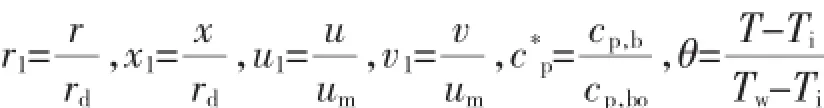
将式(8)无量纲化:
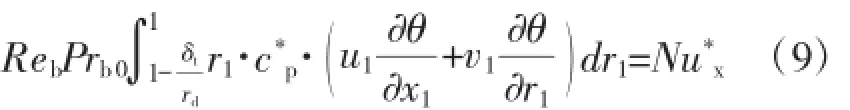
将式(9)写成矢量形式:
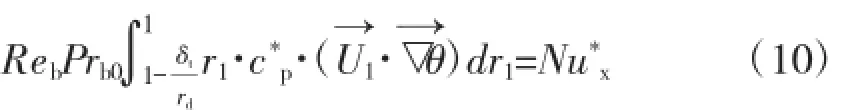
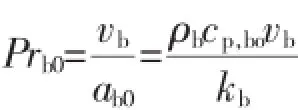
方程(10)进一步可写成:
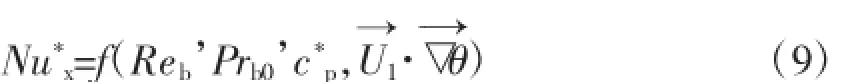
式中ρb—微胶囊相变悬浮液的整体密度,kg/m3;
um—微胶囊相变悬浮液在管内的整体平均速度,m/s;
u—微胶囊相变悬浮液在管内的轴向瞬时速度,m/s;
v—微胶囊相变悬浮液在管内的纵向瞬时速度,m/s;
cp,b0—未发生相变时微胶囊相变悬浮液的整体比热容,kJ/(kg·K);
vb—微胶囊相变悬浮液的整体运动粘度,m2/s;
ab0—未发生相变时微胶囊相变悬浮液的热扩散系数,m2/s。
由式(10)可以看出,Reb、Prb0、以及是影响Nu*x的主要因素,其中等效比热容c*p代表了相变所独有的特性。由于微胶囊相变悬浮液内含有相变材料,发生相变时产生相变潜热。为了简化,将相变潜热等效为微胶囊相变悬浮液的表观比热容,则总表观比热容增大。
微胶囊相变材料的相变过程是在一定温度范围内发生相变,而不是一个恒定的温度点。张寅平等[15]分析了相变微胶囊在换热过程中有四种不同的比热容随温度变化的曲线,但其面积是一样的(如图1所示)。在热充分发展阶段,四种比热容-温度曲线对传热影响差异很小。因此,本文采用相变微胶囊的矩形cp-T曲线。
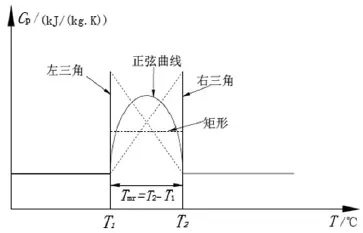
图1 相变微胶囊的cp-T曲线(假设除比热容外,悬浮液的其他物性均为常数)
在相变温度范围内,悬浮液的整体比热容可通过下式计算:

式中cp—微胶囊相变颗粒的比热容,kJ/(kg·K);
cf—微胶囊相变悬浮液的载流体的比热容,kJ/(kg·K)。
因此,在传热的整个过程中,比热容计算式如下:
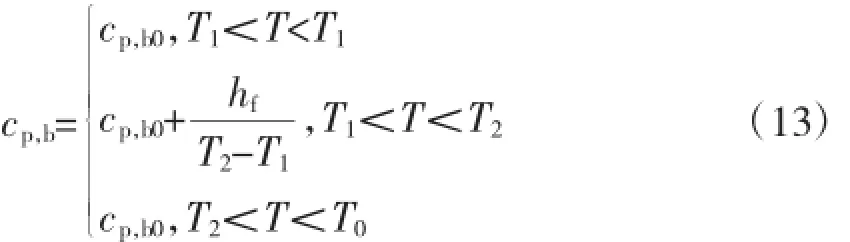
另一方面,微胶囊相变材料在悬浮液中一直保持球形固态,增加了相变材料与周围流体之间的换热表面积。同时,在流动过程中,微胶囊颗粒与周围载流体之间的相对涡旋运动产生“微对流效应”[22]。这两者可等效为悬浮液有效导热系数的增大,有利于换热。微胶囊相变悬浮液有效导热系数广泛采用Charunyakorn给出经验关系式[6]来计算:
Maxwell’s关系式[5]:
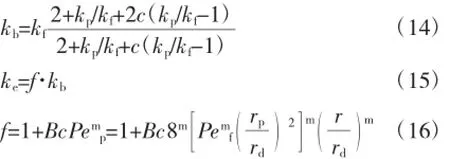
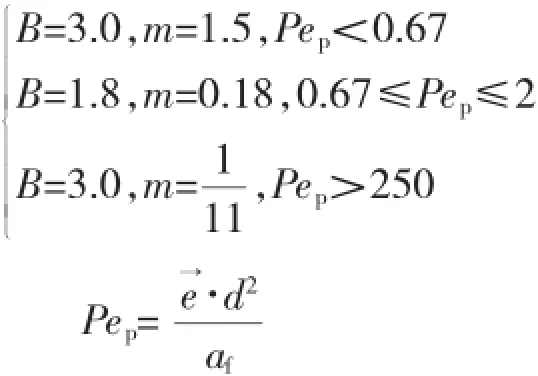
式中ke—微胶囊相变悬浮液的有效导热系数,W/(m·K);
kp—微胶囊相变材料的导热系数,W/(m·K);
kf—悬浮液载流体的导热系数,W/(m·K);
rp—微胶囊相变颗粒的半径,μm;
af—周围载流体的热扩散系数,m2/s。
等效比热容c*p和有效导热系数ke是微胶囊相变悬浮液区别于单相流体强化换热的主要影响因素。综上分析,影响微胶囊相变悬浮液强化换热的因素有:对于微胶囊相变材料,物性参数(密度、粘度、比热容等)、体积浓度、颗粒大小、过冷度、相变温度区间、等效比热容随温度变化的曲线形状等;对于圆管,加热热流密度和管径大小;对于流动情况,雷诺数、流态(层流或湍流)和粘性(与流动阻力有关)。但这些影响因素不是相互独立的,而是相互影响、相互作用的。
3 模型建立及求解
3.1几何模型的建立及网格划分
在进行模拟时,为了简化分析,需做出如下基本假设:
(1)管流为层流,且速度充分发展;
(2)流体入口温度不大于微胶囊相变开始相变温度;
(3)微胶囊颗粒均匀分布在水中。当体积浓度c≤25%时,可视为牛顿流体;
(4)忽略粘性耗散和轴向导热,且无内热源或内热汇;
(5)忽略密度差,且热壁面附近无颗粒层影响;
(6)除等效比热容是温度的函数外,微胶囊相变悬浮液其他物性均为常数。
加热管段的二维几何模型如图2所示,该圆管是内径为4mm、厚度为1mm、长度为3.7m的不锈钢管,忽略壁厚对管壁温的影响。利用ICEM CFD对该几何模型进行四边形结构网格划分,网格数为155400。
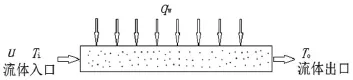
图2 加热管段的二维几何模型
3.2多相流模型
在Fluent软件中,多相流模型主要包括离散模型(DPM)、流体体积函数(VOF)模型、混合(Mixture)模型和欧拉(Eulerian)模型。DPM中有连续相和离散相,而且离散相的体积分数应很低。而VOF模型适用于分层的或自由表面流,Mixture模型和Eulerian模型适用于流动中有相混合或分离,或分散相的体积分数不太低。Mixture模型要求分散相可以相对均匀分布在连续相中,且比欧拉模型少求解一些方程,但精度会低于欧拉模型[23]。
本模拟中的流动介质是微胶囊相变悬浮液,而且体积浓度范围是5%~15%。综合考虑各种多相流模型的适用条件和应用范围,最终选择Mixture模型,在满足模拟精度要求的前提下,计算量会比Eulerian模型少。
3.3微胶囊相变悬浮液的设置
在Fluent设置中,选择Mixture模型,主相是水,第二相是微胶囊相变材料,分别设置其物性大小(包括密度、比热容、导热系数、粘度等参数的设置),并设置其相应粒径大小,见表1所示。然后设置几何边界条件和热边界条件(即加热热流密度),对边界条件进行初始化(此时需要设置悬浮液中微胶囊相变的体积浓度)。采用SIMPLE算法和二阶差分格式进行迭代计算。

表1 微胶囊相变及其悬浮液的物性参数[15]
4 模拟结果与分析
4.1强化换热分析
(1)图3显示,微胶囊相变悬浮液的修正换热系数比γ随c增大而提高,而管道壁面温度Tw随之降低,并均低于水。在c=20%时,修正换热系数比γ约为1.9~2.2,Tw比水降低25%左右。
体积浓度的高低,直接关系到换热过程中相变吸收潜热的多少,即单位体积悬浮液表观比热容的大小。同时微胶囊颗粒数量的增加加剧了其与周围流体之间的“微对流效应”,使有效导热系数增大,最终改变温度场,强化换热。
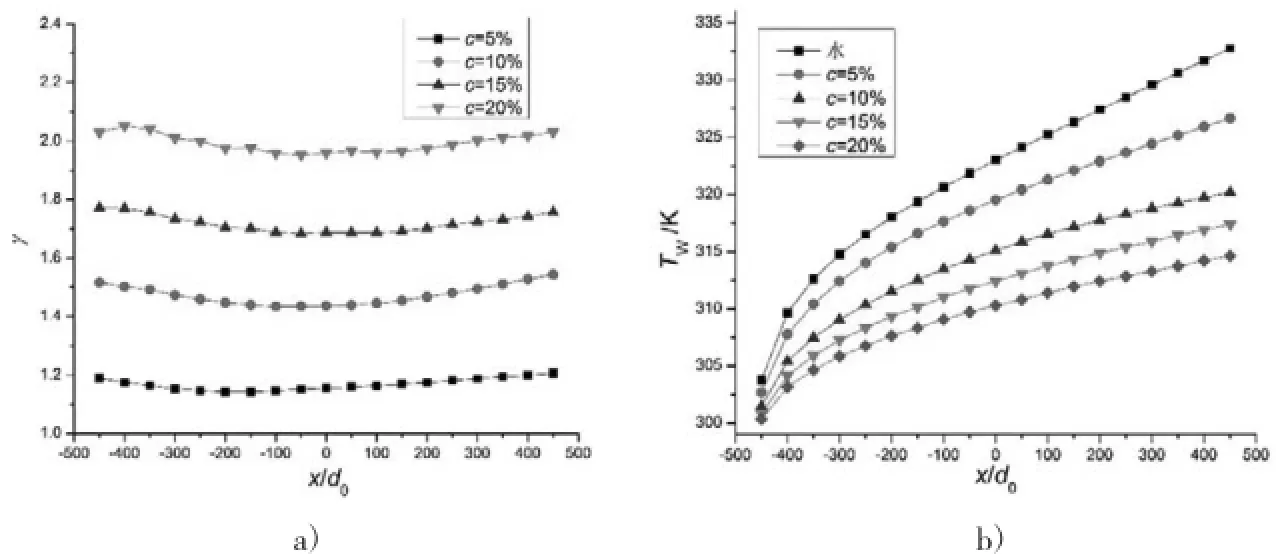
图3 不同体积浓度c的γ和Tw变化曲线(Ste=2.606,d=4mm,dp=18μm,Re=1000,ML=0,MR=0.27)a)γ曲线图b)Tw曲线图
(2)图4表明,在相同条件下,微胶囊相变悬浮液的修正换热系数比γ随Re增大而增大,Tw随之降低。当c=10%、Re=1000时,修正换热系数比γ约为1.45~1.53,Tw比水降低15%左右。
(3)斯蒂芬(Stefan)数也是影响微胶囊相变悬浮液强化换热的一个因素。据式(5)可知,在其他条件不变时,影响Ste的唯一因素是加热热流量qw,且与之成正比。图5表明,随Ste的增加,微胶囊相变悬浮液的修正换热系数比γ减小,而Tw增大,但变化均不是很显著。当Ste=2.606时,修正换热系数比γ约为1.45~1.54,Tw比水降低16%左右。
(4)ML是无量纲的过冷度,即微胶囊相变材料开始发生相变的温度与悬浮液入口温度之差的无量纲量。过冷度越大,说明相变材料开始发生相变的时间越晚。由图6可知,微胶囊相变悬浮液的修正换热系数比γ随ML增加而减小,管壁温Tw也随之降低。当ML=0.15时,修正换热系数比γ约为1.30~1.5,Tw比水降低18%左右。过冷度的增大会减弱悬浮液的换热效果。
(5)MR是无量纲的相变温度区间,即微胶囊相变颗粒相变结束温度与相变开始温度之差的无量纲量。如图7所示,微胶囊相变悬浮液的修正换热系数比γ随MR增加而减小,而管壁温Tw随之降低。当MR=0.38时,修正换热系数比γ约为1.47~1.53,Tw比水降低15%左右。
(6)由图8可知,随微胶囊相变颗粒直径dp的增大,微胶囊相变悬浮液的修正换热系数比γ会增大,而Tw有所降低,但不明显。当dp=100μm时,修正换热系数比γ约为1.7~1.85,Tw比水降低20%左右。
4.2压降分析
粘度是影响微胶囊相变悬浮液流动换热的重要因素之一,其粘度大于水的粘度[3,4]。一些学者[7,10,21]在对微胶囊相变悬浮液的换热性能进行实验研究时,给出微胶囊相变悬浮液的粘度随体积浓度和温度的变化曲线,得出体积浓度越大,粘度越大,而温度的影响很小,基本可以忽略不计。粘度的增大会导致悬浮液在管内流动时压降增大,阻力损失增多,功耗增加。
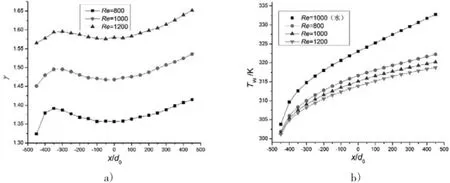
图4 不同雷诺数Re的γ和Tw变化曲线(Ste=2.606,d=4mm,dp=18μm,c=10%,ML=0,MR=0.27)a)γ曲线图b)Tw曲线图
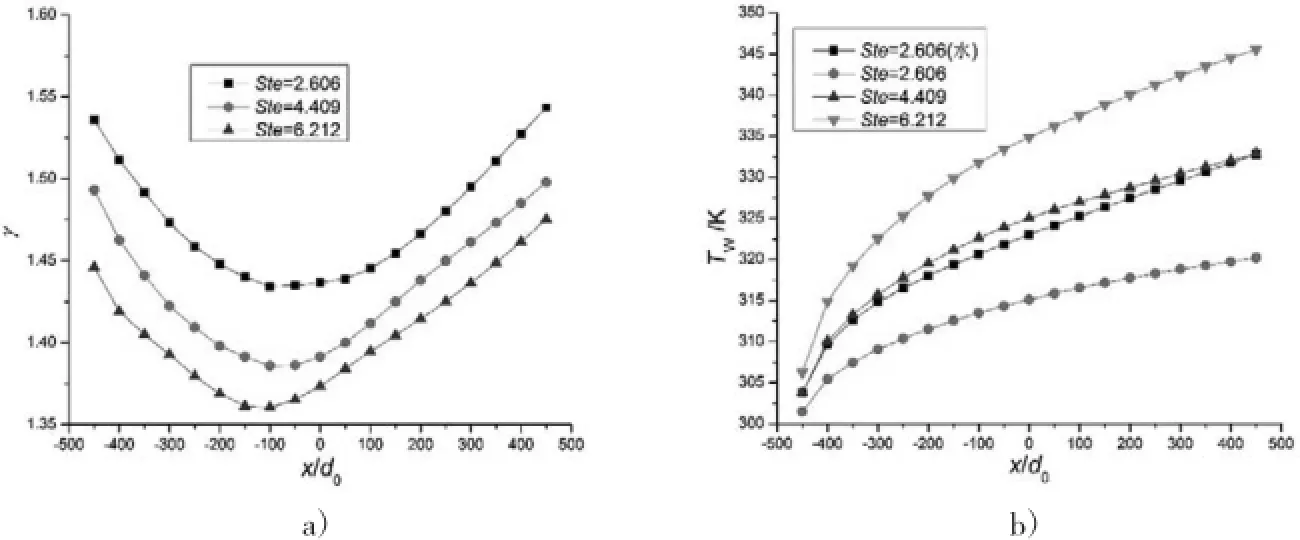
图5 不同Ste数的γ和Tw变化曲线(c=10%,d=4mm,dp=18μm,Re=1000,ML=0,MR=0.27)a)γ曲线图b)Tw曲线图
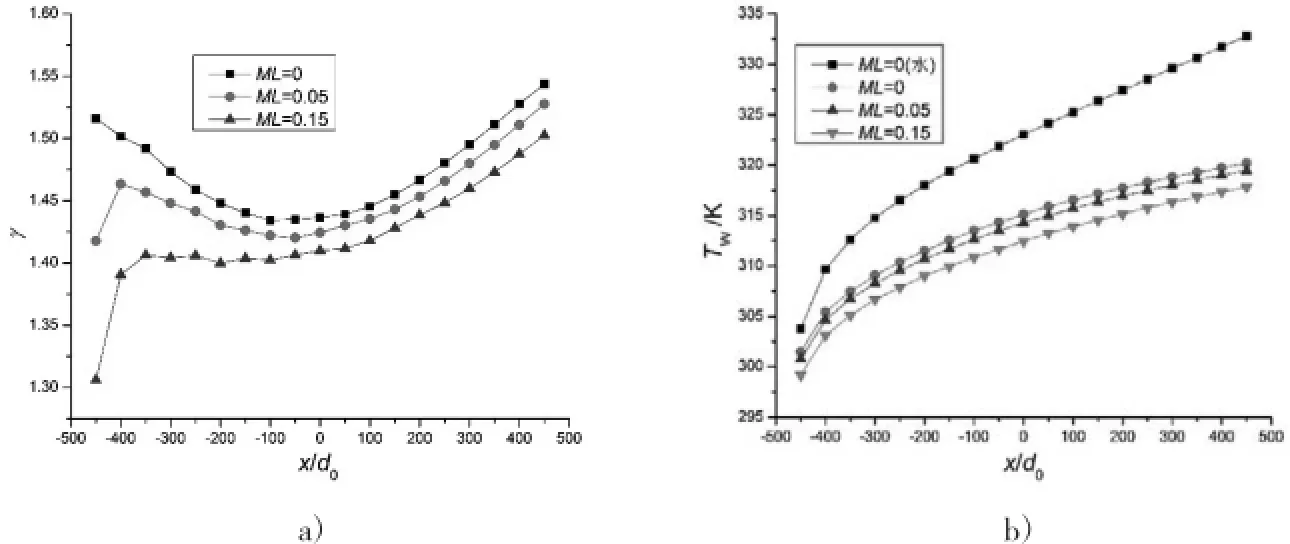
图6 不同过冷度ML的γ和Tw变化曲线(Ste=2.606,d=4mm,dp=18μm,Re=1000,c=10%,MR=0.27)a)γ曲线图b)Tw曲线图
图9a)表明,体积浓度越大,压力变化曲线越陡峭,进出口压降越大,并大于水。相同雷诺数下,当体积浓度为15%时,微胶囊相变悬浮液的压降达到水的15倍左右。图9b)是水和不同浓度的微胶囊相变悬浮液在管内流动的进出口压降值随流动速度的变化。流速u越大,其压降越大。
对于微胶囊相变悬浮液,当体积浓度低于25%时,表现出牛顿流体的特征[7]。为了更好的分析微胶囊相变悬浮液的粘度对其流动和换热的影响,定义了一个热-动力性能比ε来综合评价微胶囊相变悬浮液在管内流动时的换热和动力性能,见公式(17),分母表示微胶囊相变悬浮液和单相流体换热性能之比,分子表示两种流体在管内流动时摩擦系数之比。
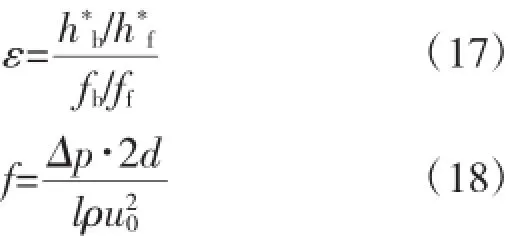
式中f—流体的摩擦系数;
fb—微胶囊相变悬浮液的摩擦系数;
ff—单相流体的摩擦系数;
Δp—流体在管道内的进出口压降,Pa;
l—管道长度,m;
ρ—管内流体密度,kg/m3;u0—管内流体的平均速度,m/s。由图10可知,微胶囊相变悬浮液在管内流动的热-动力性能比ε随体积浓度的增加而增大,但其增幅却越来越小,表明因体积浓度增加而导致的粘度增大对流体流动产生的不利影响越来越大。当体积浓度较高(如大于30%)时,微胶囊相变悬浮液可能会表现出非牛顿流体的特征,此时,阻力损失会大大增加,有可能抵消掉强化换热的优势。因此,在实际应用中需要综合考虑换热性能和流动阻力的影响,适当的选取体积浓度的大小。另外也可考虑添加适量的减阻剂降低阻力损失等。
5 结语
(1)本文提出修正换热系数比γ来表征不同影响因素对微胶囊相变悬浮液强化换热的影响程度。
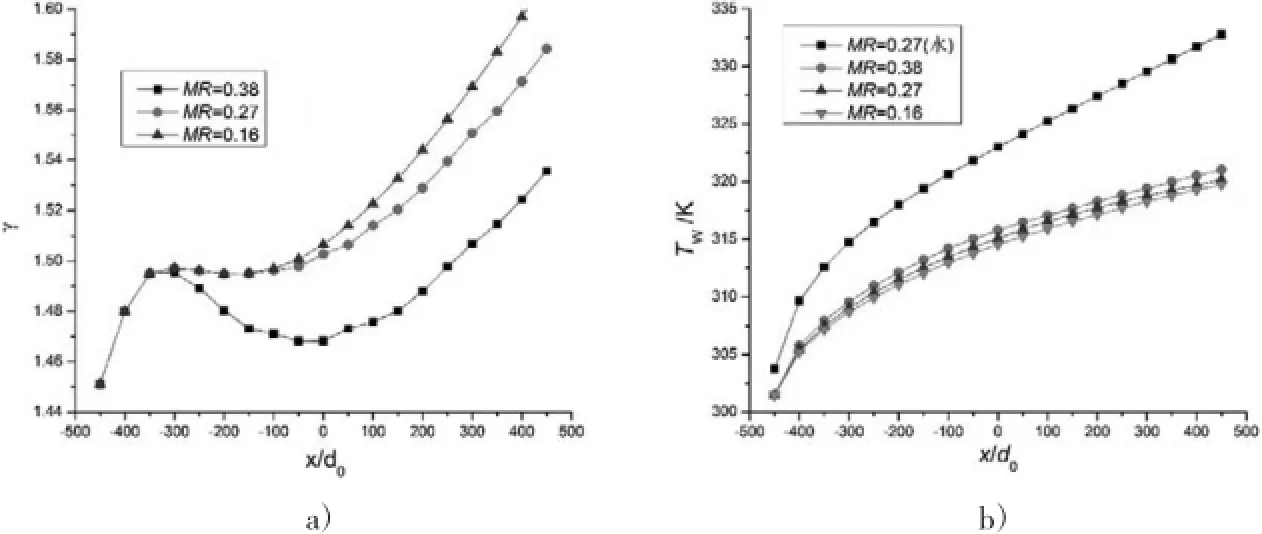
图7 不同相变温度区间MR的γ和Tw变化曲线(Ste=2.606,d=4mm,dp=18μm,Re=1000,c=10%,ML=0)a)γ曲线图b)Tw曲线图
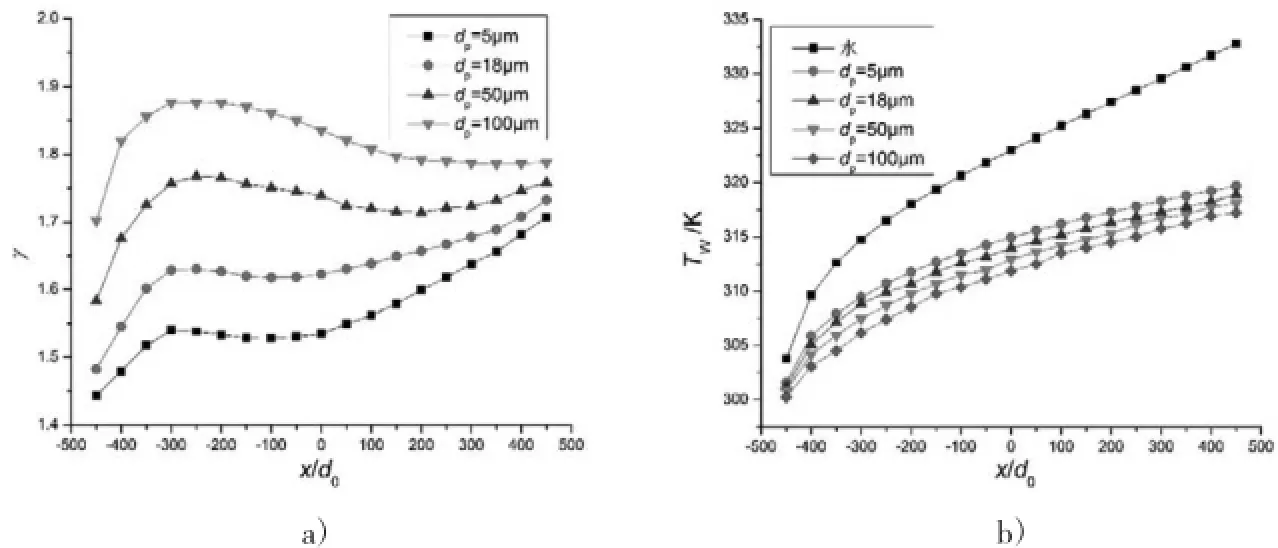
图8 不同粒径dp的γ和Tw变化曲线(Ste=2.606,d=4mm,Re=1000,c=10%,ML=0,MR=0.27)a)γ曲线图b)Tw曲线图
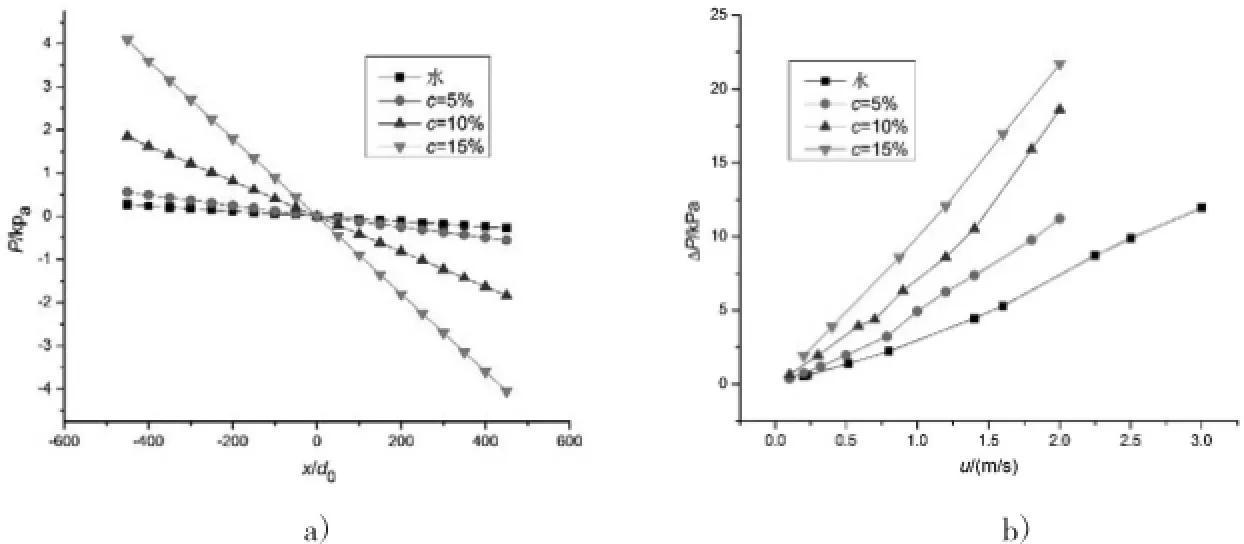
图9 不同体积浓度的微胶囊相变悬浮液压力和压降变化(Ste=0.803,d=4mm,dp=18μm,ML=0,MR=0.27)a)压力P随c变化(Re=1000)b)压降ΔP随u变化
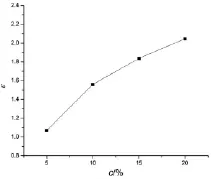
图10 热-动力性能比ε随体积浓度的变化(Ste=0.803,d=4mm,dp=18μm,Re=1000,ML=0,MR=0.27)
(2)体积浓度c是影响微胶囊相变悬浮液强化换热的主要因素。微胶囊相变悬浮液的修正换热系数比γ随c的增加而增大。当c=20%时,修正换热系数比γ约为1.9~2.2,管壁温降低约25%。
(3)斯蒂芬数Ste也是影响微胶囊相变悬浮液强化换热的一个不可忽略的因素,但是其影响程度并不如某些已有文献中那么显著[5~22]。所以,有关Ste对悬浮液强化换热的影响还有待进一步的研究。
(4)雷诺数Re、过冷度ML、相变温度区间MR、微胶囊颗粒直径dp等对微胶囊相变悬浮液换热的影响不可忽略,但效果均不是很显著。对于过冷度,在保证相变材料完全发生相变的前提下,需尽量减小过冷度大小。
(5)当c小于25%时,微胶囊相变悬浮液的热-动力性能比ε随c的增大而增幅越来越小,说明c并不是越大越好,过高的c可能导致其粘度带来的负面作用,如阻力损失等,已超过其对换热的强化作用。
(6)本文微胶囊相变悬浮液是以水为载流体。虽然它在强化传热方面表现出很大的优势,但其存在问题之一就是导热系数不高。后续的研究可以考虑使用其他流体(如导热系数相对较高的流体等)作为其载流体,或添加一定的添加剂来提高其导热系数,强化换热。
[1]Yamagishi Y,Sugeno T,Shige T.An evaluation of microencapsulated PCM for use in cold energy transportation medium[R].IEEE Paper,1996:96~82.
[2]Inaba H.New challenge in advanced thermal energy transportation using functionally thermal fluids[J].International journal of thermal sciences,2000,39(9):991~1003.
[3]张寅平.储热及传热新材料—功能热流体简介[J].自然杂志,1998,20(1):51~56.
[4]Zhao C.Y,Zhang G.H.Review on microencapsulated phase change materials(MEPCMs):fabrication,characterization and applications[J].Renewable and Sustainable Energy Reviews,2011,15(8):3813~3832.
[5]Kassa K.E.and Chen M.M.Improvement of the performance of solar energy or waste heat utilization system by using phase-change slurry as an enhanced heat-transfer storage fluid[J].Journal of Solar Energy Engineering,1985,V107:229~236.
[6]Charunyakorn P,Sengupta S,Roy S.K.Forced convection heat transfer in microencapsulated phase change material slurries:flow in circular ducts[J]. International Journal of Heat and Mass Transfer,1991,34(3):819~833.
[7]Yamagishi Y,Takeuchi H,Pyatenko A.T,Kayukawa N.Characteristics of microencapsulated PCM slurry as a heat-transfer fluid[J].AIChE Journal,1999,45(4):696~707.
[8]Goel M,Roy S.K,Sengupta S.Laminar forced convection heat transfer in microencapsulated phase change material suspensions[J].International journal of heat and mass transfer,1994,37(4):593~604.
[9]Wang X.C,Niu J.L,Li Y,et al.Flow and heat transfer behaviors of phase change material slurries in a horizontal circular tube[J].International Journal of Heat and Mass Transfer,2007,50(13):2480~2491.
[10]Alvarado J.L,Marsh C,Sohn C,et al.Thermal performance of microencapsulated phase change material slurry in turbulent flow under constant heat flux[J].International Journal of Heat and Mass Transfer,2007,50(9):1938-1952.
[11]Roy S.K,Avanic B.L.Laminar forced convection heat transfer with phase change material emulsions[J].International communications in heat and mass transfer,1997,24(5):653~662.
[12]Roy S.K,Avanic B.L.Laminar forced convection heat transfer with phase change material suspensions[J].International communications in heat and mass transfer,2001,28(7):895~904.
[13]Roy S.K,Avanic B.L.Turbulent heat transfer with phase change material suspensions[J].International journal of heat and mass transfer,2001,44(12):2277~2285.
[14]Zhang Y,Faghri A.Analysis of forced convection heat transfer in microencapsulated phase change material suspensions[J].Journal of Thermophysics and Heat Transfer,1995,9(4):727~732.
[15]Hu X,Zhang Y.Novel insight and numerical analysis of convective heat transfer enhancement with microencapsulated phase change material slurries:laminar flow in a circular tube with constant heat flux[J].International Journal of Heat and Mass Transfer,2002,45(15):3163~3172.
[16]张寅平,胡先旭.等热流圆管内潜热型功能热流体层流换热的内热源模型及应用[J].中国科学(E辑),2003,33(3):237~244.
[17]Bai F.W.,Lu W.Q.Numerical analysis of laminar forced convection heat transfer in microencapsulated phase change material suspension[J].Journal of Enhanced Heat Transfer,2003,10(3):311~322.
[18]Wang X.,Zhang Y.P.,Hu X.X.Turbulent heat transfer enhancement of microencapsulated phase change material slurries with constant wall heat flux[J].Journal of Enhanced Heat Transfer,2004,11(1):13~22.
[19]Hao Y.L.,Tao Y.X.A numerical model for phase-change suspension flow in microchannels[J].Numerical Heat Transfer,2004,46(1):55~77.
[20]郝睿.微胶囊相变悬浮液的管内层流强化传热性能研究[D].天津:天津大学硕士论文,2004.
[21]Chen B,Wang X,Zeng R,et al.An experimental study of convective heat transfer with microencapsulated phase change material suspension:laminar flow in a circular tube under constant heat flux[J].Experimental Thermal and Fluid Science,2008,32(8):1638~1646.
[22]赵镇南,郝睿,王利.固液两相流中微对流强化的机理分析与数值模拟[J].工程热物理学报,2005,26(4):656~658.
[23]江帆,黄鹏.FLUENT高级应用与实例分析[M].北京:清华大学出版社,2008.
[24]Zhang X.X,Fan Y.F,Tao X.M,et al.Crystallization and prevention of supercooling of microencapsulated n-alkanes[J].Journal of Colloid and Interface Science,2005.281(2):299~306.
Theoretical Research on Laminar Forced Convective Heat Transfer with Microencapsulated Phase Change Material Slurries in a Circular Tube
ZHU Huan-huan,LI Peng
(School of Mechanical Engineering,Tongji University,Shanghai 201804,China)
Based on the soft of Fluent,the microencapsulated phase change material slurries(MPCMs)were studied for the forced convective heat transfer enhancement of laminar flow in a circular tube under constant heat flux by numerical simulation.A ratio of correctional heat transfer coefficient(γ)is used to analyze the influence of various factors.The predicting results show that the volume concentration(c)is the main factor influencing the heat transfer enhancement.The γ increases with the rise of c,and can be bigger than 2.Moreover,the rise of wall temperature can be reduced by about 25%. The increase of Reynolds number and particle diameter,and the decrease of heat flux,the phase transition temperature range and the degree of super-cooling are all conducive to the heat transfer enhancement with MPCMs.Finally,a thermaldynamic performance ratio(ε)is defined to evaluate heat transfer and flow properties of the MPCMs.Simulation results of this paper on the MPCMs will provide a foundation for its further studies.
microencapsulated phase change slurry;laminar forced fluid;heat transfer enhancement;theoretical research
10.3969/J.ISSN.2095-3429.2015.05.013
TU83
A
2095-3429(2015)05-0051-08
朱换换(1991-),女,安徽人,在读研究生,主要从事空调制冷新技术、微胶囊相变材料等方面研究;李芃(1972-),女,山东人,副教授,主要从事空调制冷新技术、建筑节能和可再生能源利用方面研究。
2015-09-09
2015-10-21
