孔道弯曲条件下拉力型锚索锚固段剪应力分布弹性理论分析

于 贵，朱宝龙，索玉文，巫锡勇

(1.中铁西北科学研究院有限公司，甘肃兰州 730000;2.西南科技大学土木工程与建筑学院，四川绵阳 621010;3.西南交通大学地质工程系，四川成都 610031)

预应力锚索由于其本身加固性能良好且经济合理，在岩土工程等领域得到了广泛应用。预应力锚索的锚固能力研究很重要，其中较为关键的是如何确定锚固段中浆体和岩体之间的剪应力分布情况，从而在对预应力锚索锚固段进行设计时考虑剪应力的分布情况使得锚固段设置合理，达到物尽其用的效果。

国内外很多专家对预应力锚索锚固段剪应力规律进行了较为深入的研究。在国外，Li等［1］提出了锚固段剪应力分析模型。Ghadimi等［2］研究得到锚固段剪应力指数型分布型式。在国内，肖淑君等［3］基于弹塑性理论，研究了拉力型锚索锚固段剪应力、位移分布特征。贺建清等［4］基于Mindlin位移解，推导出锚固段轴向应力和剪应力分布的理论解。陈棠茵［5］运用剪切位移传递法，建立了抗浮锚杆计算模型，推导了锚侧剪应力与剪切位移的关系式。何思明等［6］将岩体剪切损伤理论与常规剪切位移法相结合，研究了拉力型预应力锚索锚固段的荷载-位移特性、侧阻力分布特性以及轴力分布特性。李桂臣等［7］利用Kelvin问题解与Boussinesq问题解推导出注浆前后锚固体与孔壁之间剪应力分布理论解析式。芮瑞等［8］分析了轴向应变与切向剪应力的分布规律。但以上学者均是对锚索孔道直线状态下锚固段周围剪应力进行的分析与计算，对于锚索孔道弯曲情况下锚固段周围剪应力分布情况鲜有涉及。

一般来说，随着锚索设计长度加大，由于施工技术有限，钻孔机械的钻头受自重影响下沉而导致下悬臂下沉，钻孔深度越大下沉的幅度也就越大，在钻孔时就难以钻成直孔，因此锚索孔道一般会呈向下弯曲状态［9］。除此之外，地质因素也是造成锚索孔道弯曲的主要因素之一［10～11］。先前关于锚索锚固段剪应力的研究均采用理想化的直线型锚固段模型来分析锚固段的剪应力分布是不准确的。因此，针对拉力型预应力锚索孔道弯曲情况下锚固段周围的剪应力进行二维弹性理论分析，对于掌握锚索锚固段真实受力状态具有一定意义。

1 锚固段力学模型

拉力型预应力锚索的预应力是先作用在锚索自由段，由自由段将力传递给锚固段。忽略锚索自由段在预应力施加过程中的损失值，设锚固段受到的拉力F即为施加在自由段的预应力。锚固体通过浆体将受到的拉力F传递给周围的岩体，从而在浆体与岩体接触面上形成了沿接触面分布的剪应力τ，方向与拉力方向相反。假设孔道在自由段或从锚固段与自由段连接处开始弯曲，整体的弯曲半径为R，锚固段弯曲处内侧和外侧上的剪应力不相等，分别用τ内、τ外来表示，如图1。

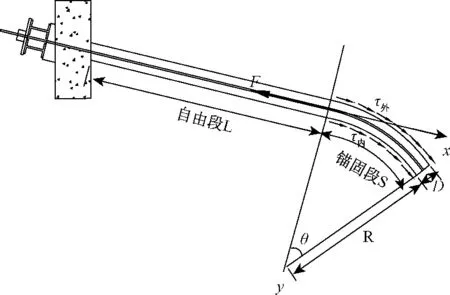
图1 孔道弯曲条件下拉力型锚索受力情况Fig.1 Schematic anchor force conditions of borehole deviation

在实际受力情况下，锚固段除了受到沿锚索体方向的拉力F外，它还会受到周围及上方土体的压力作用。根据圣维南原理，忽略除拉力以外的其他面力对锚索锚固段的作用。另外，一般锚索锚固段均具有一定的直径，不能将其粗略地当作一条直线来计算，又因锚固段有一定的弯曲，此处只讨论孔道弯曲后锚固段锚固体内侧剪应力τ内与外侧剪应力τ外的分布情况。图2为简化后的拉力型预应力锚索锚固段力学分析模型。

图2 锚索锚固段力学分析模型Fig.2 Mechanical model of the anchorage segment

2 锚固段剪应力分布二维弹性理论分析

根据弹性理论［12］(图3)，在半平面体边界O点处受到集中力F作用。在已知集中力F的大小，作用方向即与x轴的夹角用β表示，以及所求点的矢径ρ和其角度φ的情况下，可以求出O点在集中力F作用下的应力。

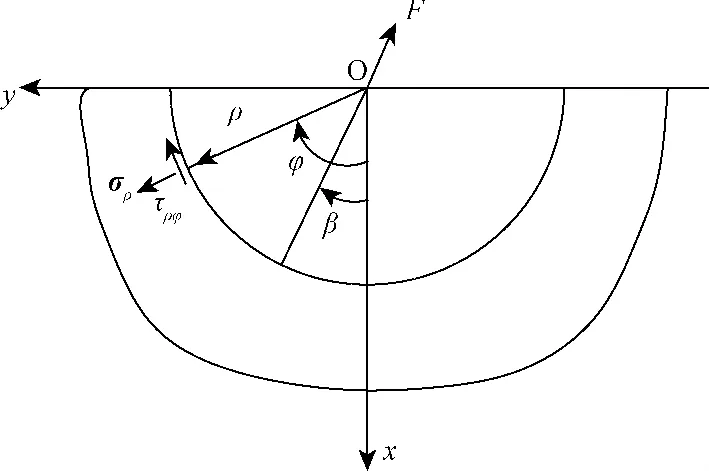
图3 半平面体内任意点在极坐标下应力分量Fig.3 Half-plane stress components in the polar coordinates

根据力学模型可知边界集中力F垂直于直线边界，这种情况下的应力分量只需在(1)式中取β=0，于是得

如图4，按照弹性理论关于平面问题中的应力分量由极坐标向直角坐标的变换式，可得

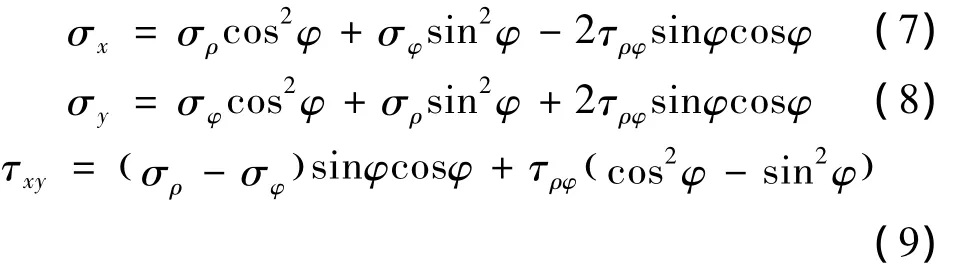
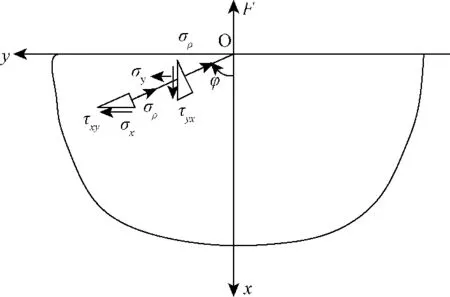
图4 半平面体内任意点在直角坐标下应力分量Fig.4 Half-plane stress components in the Cartesian coordinate system

将式(4)、(5)、(6)代入式(7)、(8)、(9)，并换算成直角坐标，可得

假设图2中受力模型为弯曲的的圆柱体，将其中的内曲线和外曲线用x、y的函数关系式表示，可得内曲线、外曲线分别为:

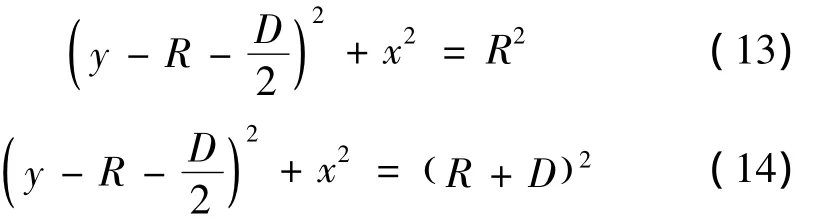
再式将(13)、(14)代入式(10)、(11)、(12)可得内曲线与外曲线的应力状态。

内曲线:

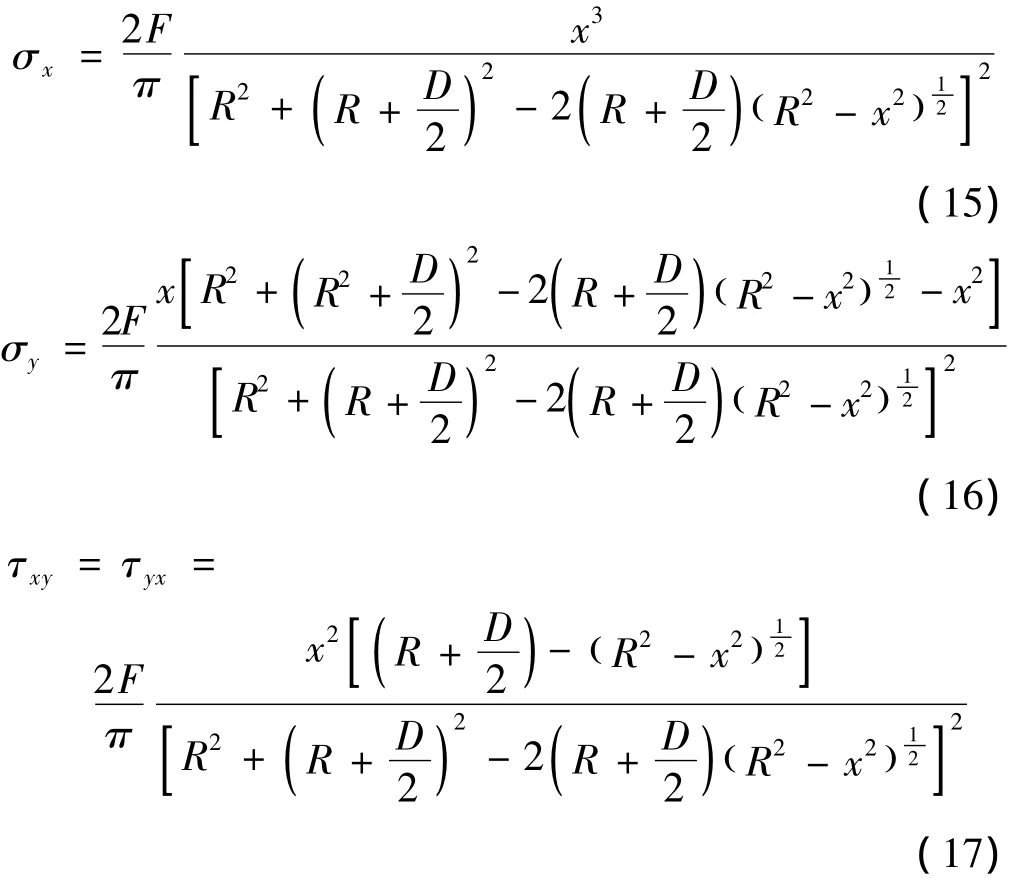
外曲线:

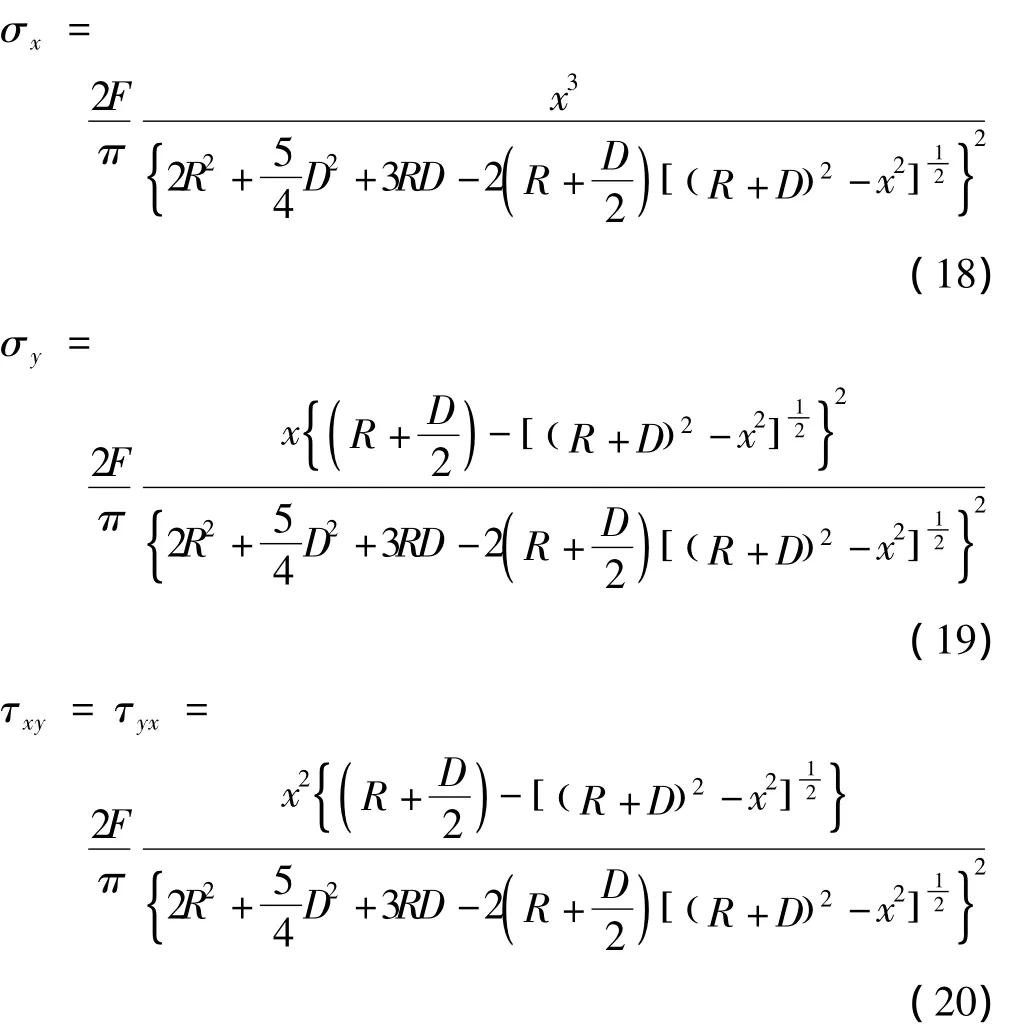
对图2进行进一步细化得图5。AB为弧MN过点C的切线，Q为弧MN的圆心，过圆心Q与点C的连线与y轴的夹角为θ'。所要求的剪应力τ为沿AB方向的，可由C点处各个应力分量合成得到。由图可以清晰的看到应力 σx、τyx与 AB的夹角为 θ'，应力σy、τxy与 AB 的夹角为 π/2-θ'。设锚固段任一点至锚固段与自由段连接处的的距离为s，内曲线上任一点C处的弧线长为s1，外曲线上任一点E处的弧线段长为 s2，可得

内曲线:

联立式(21)、(22)，可知

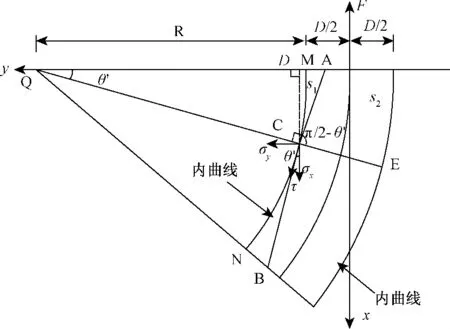
图5 锚固段上任一点处的应力Fig.5 Stress of the anchoring segment

外曲线:

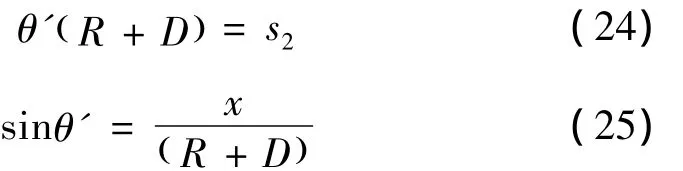
联立式(24)、(25)，可知

根据图5所示曲线上的任一点的应力关系，可以得到锚固段剪应力分布关系式:

将式(15)～(17)、(22)～(23)代入式(27)即可得到锚索锚固段内曲线上的剪应力沿内曲线s1的变化关系式 τ(s1)。同理，将式(18)～(20)、(25)～(26)代入式(27)即可得到锚索锚固段外曲线上的剪应力沿外曲线s2的变化关系式τ(s2)。

3 计算实例

计算实例位于贵州省兴义市境内的汕昆高速公路K111+550处，路基沉降过大，坡表面发生过大裂缝，采用预应力锚索对碎石土路基进行加固(图6)。设计锚索长度40 m，锚固段长7 m。根据钻孔直径可计算得到锚固段直径D=0.14 m，通过采用专用设备测试钻孔孔道轨迹［13］，得出孔道弯曲半径R=10 m。计算中预拉力F分别按600 kN、800 kN和1000 kN来进行加载。将上述参数代入上述相应方程中，可分别计算得到锚固段内曲线和外曲线的剪应力分布曲线(图7～8)，其中实线为孔道弯曲情况下剪应力分布曲线，虚线为孔道直线情况下剪应力分布曲线。

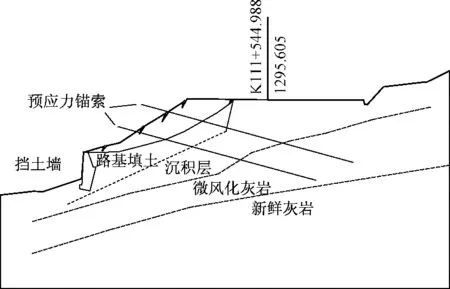
图6 预应力锚索加固路基示意Fig.6 Subgrade reinforced by the prestress anchor

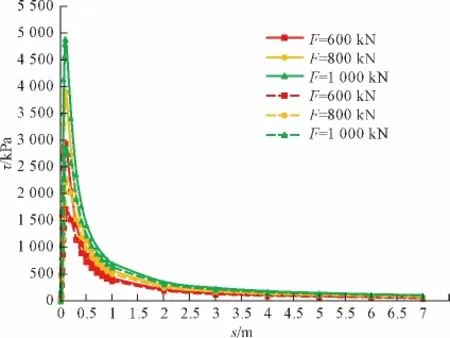
图7 锚固段内曲线的剪应力τ(s1)分布Fig.7 Stress curve of τ(s1)inside the face

由图7可以看出，剪应力自锚固段起点开始沿长度方向上逐渐增大，直至0.09 m处达到最大值后逐渐减小，直至锚固段末端趋于稳定但并不为零。由图8可以看出，剪应力自锚固段由零开始逐渐沿预拉应力方向(反方向剪应力)增大，直到0.04 m处达到极值后逐渐减小，至0.07 m处剪应力减小为零，随后沿剪应力正方向逐渐增大，到0.2 m处达到最大值后逐渐减小，最终在锚固段末端趋于稳定但并不为零。改变参数的大小，如改变锚索长度、锚索直径或者是锚索弯曲半径的大小，只会改变剪应力分布曲线的极值点、零点和最值点处的值和相应的剪应力的大小，不会改变剪应力分布曲线的形状。

图8 锚固段外曲线的剪应力τ(s2)分布Fig.8 Stress curve of τ(s2)outside the face

对比孔道弯曲与直线状态下锚固段周边剪应力的分布规律，可以得出如下规律性:

(1)孔道直线情况下锚固段周边剪应力沿同一截面相同，而孔道弯曲情况下锚固段同一截面上剪应力不同，剪应力大小处于内曲线τ(s1)和外曲线τ(s2)之间。

(2)孔道弯曲情况下锚固段内曲线上剪应力最大值比孔道直线情况下锚固段周围剪应力最大值约大2倍，而外曲线上剪应力最大值约为直线状态时的50%。主要是因为锚固段的弯曲造成弯曲内侧的浆体在预应拉力作用下施予周围岩体一个向内的压力，使其受到的摩阻力增大，导致剪应力增大;而弯曲段外侧的浆体则在预应拉力的作用下，有脱离周围岩体的趋势，导致剪应力减小。换言之，孔道直线情况下剪应力分布图被包含在孔道弯曲情况下作用在内外曲线剪应力分布图之内，说明按孔道直线情况下分析的剪应力分布较简略，不能够真实表现实际孔道弯曲情况下锚索锚固段的受力情况。

(3)孔道弯曲情况下，锚固段起点处外边缘上会在很短的距离内分布与假设方向相反的剪应力(反方向剪应力)，而孔道直线情况下却没有，主要是由于自由段锚索周围涂有润滑油，在预应力施加后可以发生较大的伸缩，带动自由段周围的岩土体发生相应程度的压缩，加之与锚固段连接处突然发生弯曲，锚固段内侧包裹着的岩体受到挤压导致这部分岩体压缩量突增。而锚固段由浆体裹握锚索钢绞线，其表面上存在着微观的粗糙皱曲，浆体围绕着钢绞线充满这些皱曲而形成一个灌浆柱整体［14～15］，灌浆柱一部分浆体嵌入到周围的岩体中，锚固段因此不容易发生较大的位移。自由段与锚固段连接处周围的岩土体相对锚固段发生了与假设剪应力正方向相反的位移，导致锚固段周围短距离内产生了反方向剪应力。

4 结论

(1)一般来说，由于施工技术原因及地质因素的作用，随着锚索长度的加大，预应力锚索钻孔孔道发生偏离、弯曲难以避免。

(2)锚索孔道弯曲情况下锚固段同一截面上剪应力并不像孔道直线状态时分布相同、均匀，而是变得不均匀，内侧剪应力大，最大值比孔道直线情况下锚固段周围剪应力最大值约大2倍，外侧剪应力小，最大值约为直线状态时的50%。

(3)由于锚索孔道弯曲效应，在锚固段起点处外侧存在反方向剪应力，更易导致注浆体的破坏。

当然，本次计算采用的是二维弹性理论模型，还需要进一步考虑基于三维弹塑性模型来探讨更接近于真实状态的锚索受力模型。

［1］ Li C，Stillborg B.Analytical models for rock bolts［J］.International Journal of Rock mechanics and Mining Science，1999，36:1013-1029.

［2］ Ghadimi M，Shahriar K，Jalalifar H.An analytical model to predict shear stress distribution in fully encapsulated rock bolts ［J］.Geotechnicaland Geological Engineering，2015，33:59-68.

［3］ Xiao S J，Chen C F.Mechanical mechanism analysis of tension type anchor based on shear displacement method［J］.Journal of Central South University of Technology，2008，15:106-111.

［4］ 贺建清，胡成兵，张建超.基于Mindlin解的压力型锚杆锚固段的受力分析［J］.水文地质工程地质，2012，39(1):47-52.［HE J Q，HU C B，ZHANG J C.Mechanical analysis of anchorage segment of pressure-type cable based on the Mindlin solution［J］.Hydrogeology ＆ Engineering Geology，2012，39(1):47-52.(in Chinese)］

［5］ 陈棠茵.剪切位移传递法分析抗浮锚杆应力状态［J］. 水文地质工程地质，2008，35(1):36-39.［CHEN T Y.Shear displacement transfer analysis on stress of anti-float anchor［J］.Hydrogeology ＆Engineering Geology，2008，35(1):36-39.(in Chinese)］

［6］ 何思明，王成华，吴文华.基于损伤理论的预应力锚索荷载变位特性分析［J］.岩石力学与工程学报，2004，23(5):786-792.［HE S M，WANG C H，WU W H.Analysis on loading deformation of prestressed cable based on the damage theory［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23(5):786-792.(in Chinese)］

［7］ 李桂臣，孙辉，张农，等.中空注浆锚索周边剪应力分布规律研究［J］.岩石力学与工程学报，2014，33(增刊2):3856-3864.［LI G C，SUN H，ZHANG N，etal. An investigation into shear stress distribution around hollow grouting anchor cables［J］. ChineseJournalofRock Mechanicsand Engineering，2014，33(Sup2):3856-3864.(in Chinese)］

［8］ 芮瑞，夏元友，顾金才，等.压力分散型锚索非均匀剪应力设计方法［J］.岩土工程学报，2012，34(7):1262-1270.［RUI R，XIA Y Y，GU J C，et al.Non-uniform shear stress design method for pressure-dispersive anchors［J］.Chinese Journal of Geotechnical Engineering，2012，34(7):1262-1270.(in Chinese)］

［9］ 王清标.孔道成孔工艺对锚固力损失的分析与控制［J］.山东大学学报，2009，39(4):145-148.［WANG Q B.Analysis and control of prestressing loss in construction techniques of anchor-eye［J］.Journal of Shandong University，2009，399(4):145-148.(in Chinese)］

［10］ 黄辉，牟文俊，陶林.浅析大吨位、超长孔深锚索钻孔孔斜控制［J］.探矿工程(岩土钻掘工程)，2010，37(6):71-74.［HUANG H，MU W J，TAO L.Brief analysis on hole deviation control of largetonnage and super-long hole depth anchorage cable hole［J］.Prospecting Work，2010，37(6):71-74.(in Chinese)］

［11］ 赵廷严.浅析钻孔弯曲产生的原因及预防纠正措施［J］.中国煤炭地质，2009，21(1):62-63.［ZHAO T Y.Causation of borehole deviation and measures to prevent and rectify ［J］.Coal Geology of China，2009，21(1):62-63.(in Chinese)］

［12］ 徐芝纶.弹性力学［M］.3版.北京:人民教育出版社，2002.［XU Z L.Elasticity mechanics［M］.3nd ed.Beijing:Peoples Education Press，2002.(in Chinese)］

［13］ 于贵，朱宝龙，李貌，等.基于惯性传感器的长大锚索钻孔孔道测量系统:中国，201410161748X［P］.2014-10-22.［YU G，ZHU B L，LI M，et al.Borehole measurement system of anchor based on inertial sensor:China，201410161748X［P］.2014-10-22.(in Chinese)］

［14］ 顾金才，沈俊，陈安敏，等.预应力锚索加固机理与设计计算方法研究［C］//第八次全国岩石力学与工程学术大会论文集.北京:科学出版社，2004:32-39.［GU J C，SHEN J，CHEN A M.Study on the reinforcement mechanism and calculation method for rock engineering reinforced by prestressed anchorcables［C］//Proceeding of8th Rock Mechanics and Engineering Conference of China.Beijing:SciencePress，2004:32-39.(in Chinese)］

［15］ 尤春安，战玉宝.预应力锚索锚固段界面滑移的细观力学分析［J］.岩石力学与工程学报，2009，28(10):1976-1985.［YOU C A，ZHAN Y B.Analysis of interfacial slip mechanics in anchorage section of anchor cable［J］.Chinese Journal of Rock Mechanics and Engineering，2009，28(10):1976-1985.(in Chinese)］