济南岩溶泉域地下水位、降水、气温与大尺度气象模式的遥相关

祁晓凡，李文鹏，李海涛，杨丽芝

(1.中国地质大学(北京)水资源与环境学院，北京 100083;2.山东省地质调查院，山东济南 250013;3.中国地质调查局水文地质环境地质调查中心，河北保定 071051;

4.中国地质环境监测院，北京 100081)

我国地下水供水水源地约占城市集中式饮用水供水水源地总数的一半，地下水供水人口约占集中式水源地供水人口总数的三分之一。尤其在我国北方，大部分城市以地下水水源地供水为主［1］。在我国北方典型的岩溶泉域——济南岩溶泉域，岩溶水是重要的供水水源。同时，也是济南泉水喷涌，保持“泉城”特色的重要补给水源保障。

长时间序列的水文监测数据具有不同的分类方法，如由趋势项、周期项、相关项和随机项组成［2］，或由趋势项、周期项、突变项和随机项组成［3］。趋势项为水文现象季节性或多年变化趋势，周期项为水文现象的周期变化，相关项反映水文现象的自相关性，突变项为水文现象受外部突变影响而形成的变化，随机项为除以上确定性成分之外的随机成分［2～3］。而对于长时间序列的地下水动态监测数据来说，也具有相同的特征。

从全球水文循环角度来说，降水等气象因子的变化是受大尺度海洋-大气相互作用事件(ENSO等)影响的［4～8］。大尺度气象模式具有中、低频率波动特征［9～10］，多具有较长的波动周期。

本文利用地下水位动态变化和大尺度气象模式的周期性变化特征，分析研究地下水位与大尺度海洋-大气相互作用模式间的关系。该项研究在国外已有开展，主要分布在西班牙［11］、英国［12］、加拿大［13］、美国［14～15］等地，而国内却缺乏此项研究。本文采用小波变换方法分析济南泉域地下水位、降水、气温及大尺度气象模式的周期性、显著时频域及相位关系特征，并研究它们之间的遥相关性。通过此项研究，可提高对水循环不同过程间相互联系的认识，有助于改进水文要素变化预测、增进人类对其的适应能力［13］，增强水资源管理水平。特别是对于一些水资源紧缺的国家，如中国，在地下水已经成为重要供水水源的背景下，研究大尺度气象模式与地下水位之间的遥相关，将有助于在全球气候变化背景下，合理规划利用地下水资源，缓解水资源供需矛盾，为政府水资源安全提供保障。

1 研究方法

对于具有周期性变化特征的长时间序列数据，传统的分析方法主要有序列相关性分析和傅里叶变换(Fourier Transform，FT)等方法进行分析［16］。随着人类活动的不断加剧、极端气候现象频发以及科学研究的不断深入，水循环过程中的各项要素表现的更为复杂，表征出随机性、模糊性、非线性、非平稳性和多时间尺度变化等特性。传统的分析方法在揭示上述特性时，存在一定的不足。因此，涌现出了诸如模糊分析、混沌理论、信息熵和小波分析等更加先进的方法［16］。

20世纪80年代初，在傅里叶变换基础上，发展起了小波变换分析方法(Wavelet Transform，WT)，很好地克服了傅里叶变换分析方法的缺点:采用窗口大小可变、位置可动的变窗进行频谱分析，从而能够更好地分析和揭示长时间序列数据中的局部特性(小周期)，适于研究具有多时间尺度和非平稳性的水文时间序列［16～17］。由小波变换衍生出来的交叉小波变换、小波相干谱分析方法等可定量评价两时间序列的时滞特征，其在地下水位动态、地下水资源研究方面已有较多应用［13，15，18～23］。

1.1 连续小波变换

时间序列(xn，n=1，…N)的连续小波变换可定义为xn的卷积和小波标准化，定义为:

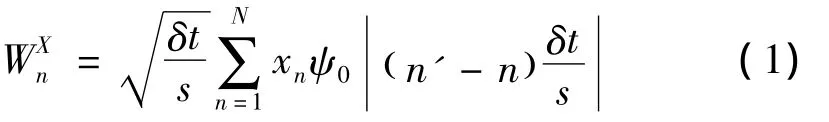
背景功率谱采用红噪声检验，红噪声检验过程用一阶自回归方程。背景红噪声功率谱定义为:

式中:α——红噪声功率谱中自回归方程的相关系数;

K——傅里叶频率系数。

连续小波变换可揭示长时间序列数据中的不同显著周期及其所处的观测时段。

1.2 交叉小波变换

交叉小波变换将2个时间序列Xn和Yn定义为，其中，*为复共轭，对应交叉小波谱为。而2个时间序列Xn和Yn的背景功率谱和PYk则定义为:

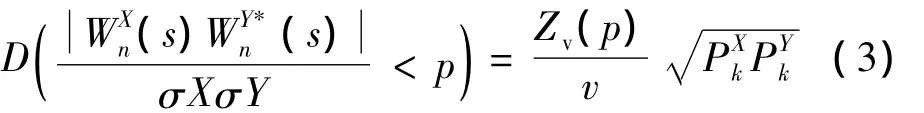
式中:Zv(p)——概率P的置信度水平，源于两个χ2分部小波谱乘积的平方根。

交叉小波的相位角定义为:

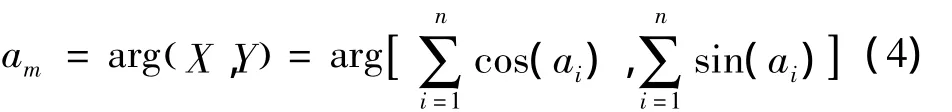
交叉小波变换可以揭示两组时间序列数据之间的相互关系，也即波动强烈时段上两组序列数据之间的关系。包括两组长时间序列数据“共同变化”的显著周期、所处时段，同时，也包括通过小波相位角分析，得到的周期先后关系。“共同变化”是指两组长时间序列数据在某时段内具有相同的波动周期，而此周期内，两组时间序列数据的波动往往具有一定的先后关系。某一因素受另外一种因素的影响而变化，它们之间会有一定的时间间隔，也称为滞后效应。如地下水水位受大气降雨的影响，而地下水水位的变化相对于降雨变化，就具有一定的时间滞后效应。

1.3 小波相干谱

对于两组时间序列数据X和Y，其小波相干谱定义为:

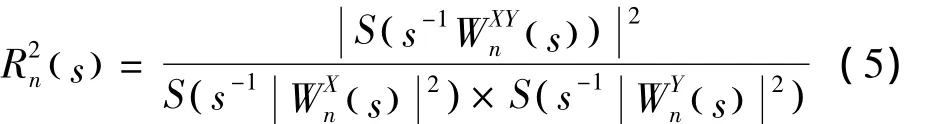
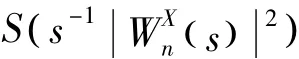
与交叉小波变换不同，小波相干谱度量两组时间序列数据局部相关的密切程度，对于两组序列数据共同变化不强烈的时段，在小波相干谱中的相关性也可能显著。小波相干谱分析弥补了交叉小波变换的不足［17，20］。

本文采用小波变换相关计算方法和程序来自Torrence 等［17］和 Grinsted 等［20］。

2 研究区概况

济南位于山东省中西部，南依泰山，北跨黄河，地处鲁中南低山丘陵与鲁西北冲积平原的交接带上，地势南高北低。济南属暖温带大陆性季风气候，多年平均气温14.3℃，多年平均降水量641.68 mm(1956—2012)。降水年内分配不均，汛期为6—9月份，平均降水量467.18 mm，占年降水量的73%，12—3月平均降水量32.03 mm，仅占全年降水量的5%。多年平均蒸发量1500～1900 mm。济南市地表水系主要包括黄河、小清河、海河三大水系。

济南泉域地质构造为单斜断块，地势南高北低，地层北倾。泉域东、西边界分别为东坞断裂和马山断裂，均为北北西向，断裂大部具阻水性质;北部以火成岩体和石炭、二叠系为界;南部以区域地表分水岭为界［21］(图1)。泉域南部为泰山山脉余脉，岩性为太古界泰山群变质岩系及古生界寒武系灰岩及页岩等，为泉域裂隙岩溶水间接补给区;中部为低山丘陵，岩性为寒武系灰岩、页岩及中、下奥陶系灰岩、泥质灰岩等，裂隙、岩溶发育，为地下水直接补给区-径流区;北部为单斜构造前缘、山前倾斜平原及黄河冲积平原等，为泉域排泄区［21］，有趵突泉泉群、黑虎泉泉群、珍珠泉泉群及五龙潭泉群等四大泉群。

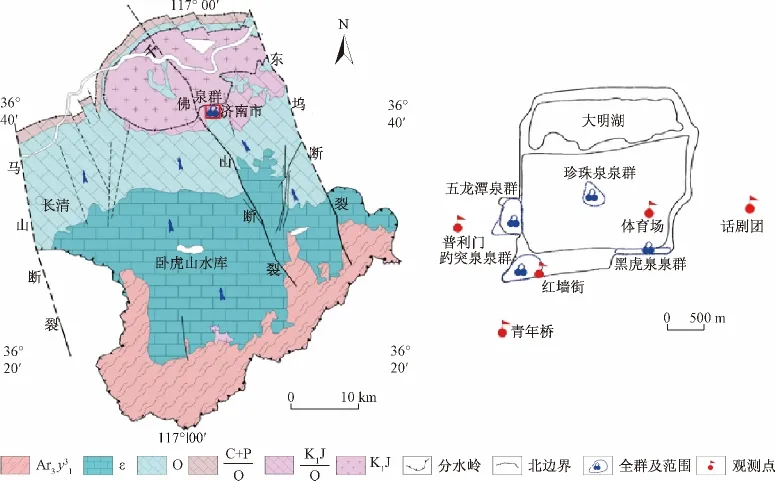
图1 济南泉域水文地质略图及观测点分布(据杨丽芝等［21］修改)Fig.1 Hydrogeological sketch map of the Jinan springs watershed and distribution of the monitoring wells

3 数据来源

3.1 地下水位动态监测数据

泉域地下水位动态数据为1959年1月—2011年12月共53年逐月观测数据(图2)，其中不同时段水位动态观测点不一致(图1，表1)。

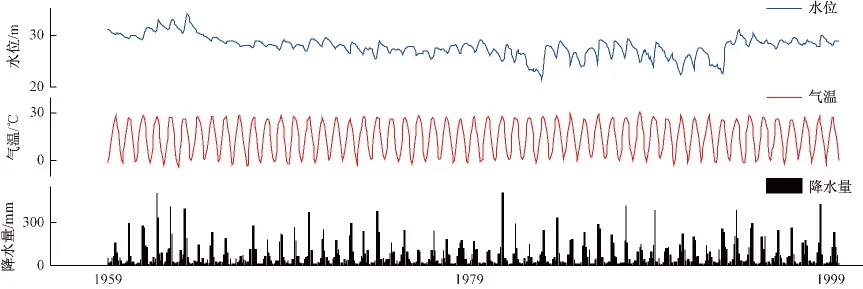
图2 地下水位、降水及气温观测数据Fig.2 Monitoring data of groundwater level，precipitationand and air temperature dynamics

表1 不同时段水位动态观测点Tab.1 Groundwater monitoring points of different time intervals

3.2 气象数据

降水及气温数据采用1959年1月—2011年12月逐月观测数据(图2)。气象数据观测站位于济南站(站号54823)，站点位于济南泉域补给区。气象数据来自于中国气象数据网(http://data.cma.gov.cn/)。

3.3 大尺度气象指标数据

大尺度气象指标包括NINO3.4区海表温度异常(NINO3.4 Sea Surface Temperature Anomaly，NINO3.4 SSTA)、南方涛动指数(Southern Oscillation Index，SOI)、北极涛动指数(Arctic Oscillation，AO)、北太平洋指数(North Pacific Index，NPI)。ENSO是全球尺度上最有影响力的遥相关模式［13］，主要有NINO SSTA和SOI两个主要特征值［6］。

NINO3.4区海表温度异常(NINO3.4 SSTA):NINO3.4 SSTA为NINO3.4区海表温度与该区多年平均海表温度的距平值，多年平均海表温度计算选取的时段为1971—2000年，NINO3.4区位于5N～5S，170～120W。数据为英国气象局(Met Office，MO)哈德利中心(Hadley Center)海表温度数据集HadISST1。

南方涛动指数(SOI):SOI是指塔希堤(Tahiti)岛(位于法属玻利尼西亚)与澳大利亚的达尔文(Darwin)站的海平面气压差，以此来定量表示南方涛动的强弱。数据来自于美国国家海洋和大气管理局(NationalOceanicand AtmosphericAdministration，NOAA)国家环境预报中心(National Centers for Environmental Prediction，NCEP)。

北极涛动指数(AO):AO定义为北半球热带外1 000hPa高度场经验正交函数分析第一模态的时间系数，是北半球中高纬度地区大气环流尺度最大、最重要的模态，对东亚气候存在影响［10］。数据来自NOAA气候预测中心(NCEP/CPC)。

北太平洋指数(NPI):NPI是位于30N、65N和160E、140W面积加权的海平面气压，数据为美国大气研究中心(National Center for Atmospheric Research，NCAR)Trenberth＆Hurrell数据集。

4 结果与分析

4.1 连续小波变换

将济南泉域地下水位、降水、气温与四个大尺度气象指标数据分别进行连续小波变换(图3)，以分析其时频域特征，了解它们的主要波动周期，以及显著周期涵盖的观测时段等信息。

图3 泉域地下水位(a)、降水(b)、气温(c)、NINO3.4 SSTA(d)、SOI(e)、AO(f)与NPI(g)连续小波变换Fig.3 Continuous wavelet transforms of(a)groundwater level，(b)precipitation，(c)air temperature，(d)NINO3.4 SSTA，(e)SOI，(f)AO and(g)NPI

4.1.1 周期性分析

4.1.1.1 地下水位、降水与气温周期性分析

连续小波变换显示(图3a～c)，泉域地下水位、降水与气温的主周期均为1a(表2)。地下水位1a的主周期在二十世纪八十年代以后显著时段分布连续;降水1a的周期在大多数观测时段均较为显著，分布稍不连续;而气温1a的周期则在全时段稳定分布。此外，降水在20世纪80年代以后有2～4a的显著周期，其周期尺度由20世纪80年代后期至21世纪初有略微减小的趋势。

表2 各指标连续小波变换的显著周期与时段Tab.2 Significant periodicities and time intervals of continuous wavelet transforms

4.1.1.2 大尺度气象指标周期性分析

NINO3.4 SSTA的主周期为1～6a，显著时段涵盖了大多数观测时段(图3d)。在1～6a的周期上，显著时频域并不完全连续，在部分观测时段NINO3.4 SSTA的周期性是不显著的。同时，该指标在不同年份的显著周期尺度也有差异，反映了周期随时间的变化。1～6a的周期主要体现在1980—2000年，其余时段上显著周期相对较短，表现为1～4a或1～5a等(表2)。

SOI主周期为2～6a与9～14a(图3e)。在2～6a周期尺度上，不同年份的显著周期也是不同的，主要趋势为由1967—1973年2～5a的周期演变为1974—1991年3～6a的周期(表2)。9～14a的长周期在1974—2008年通过了显著性检验，涵盖时段长，同样反映了SOI的主周期特征。

AO主周期为13～19a，显著时段为1972—1995年(图3f)，此外短周期尺度上有1960—1968年2～5a及1980—1988年8a左右的局部周期。

NPI的周期性更为清晰，其主周期为1a，且显著时段分布连续(图3g)。

4.1.1.3 NINO3.4 SSTA显著时段与ENSO事件强度的关系分析

对比王绍武等［9］、许武成等［6］对 ENSO 事件强度的研究成果，可知1959—2000年间全部ENSO事件的发生时间与上述5个时段有很好的对应关系，ENSO事件全部发生在上述显著时段内(表3)。如上述第一时段包含开始于1963年与1965年的两次暖事件及开始于1962年与1964年的两次冷事件。除去1a的周期，在多年周期尺度上，NINO3.4 SSTA的2～6a周期与相关研究成果［13～15］是一致的(表 3)。

表3 小波变换显著周期时段与相关文献ENSO冷暖事件对比Tab.3 Comparison between the significant time intervals of NINO3.4 SSTA continues wavelet transform and ENSO events

4.2 交叉小波变换

将四个大尺度气象指标与济南泉域地下水位、降水、气温分别进行交叉小波变换(图4)，以分析波动强烈的时段上它们共同变化的显著周期、显著时段等信息。

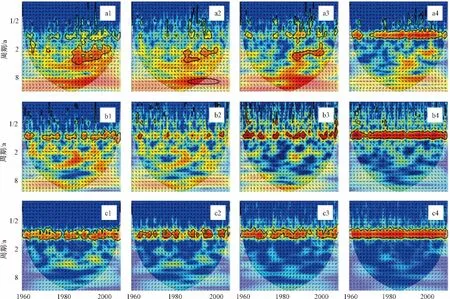
图4 NINO3.4 SSTA(1)、SOI(2)、AO(3)和NPI(4)与泉域地下水位(a)、降水(b)、气温(c)的交叉小波变换Fig.4 Cross wavelet transforms of(1)NINO3.4 SSTA，(2)SOI，(3)AO and(4)NPI with respect to(a)groundwater level，(b)precipitation and(c)air temperature

NINO3.4 SSTA与泉域地下水位的交叉小波变换显示(图4a1)，二者主要存在2～6a的共振周期，显著时段为20世纪80年代中期至2005年左右，符合NINO3.4 SSTA与地下水位连续小波变换的显著时频域特征。共振周期是小波分析里两时间序列共同变化的周期，在此周期上的显著时段内两序列是显著相关的，且会呈现出一定的相位关系，可说明两序列波动的时间间隔。在本文中显著共振周期及其时段则代表了泉域地下水位、降水、气温与大尺度气象模式的遥相关性。2～6a的周期上地下水位与NINO3.4 SSTA总体呈反相位分布，表现出了一定的遥相关。

SOI与水位动态11～13a的周期最为明显，显著时域为20世纪80年代后期至90年代(图4a2)。在20世纪80年代中期至2005年左右也存在显著的2～5a的周期，显著时频域基本在NINO3.4 SSTA与水位动态小波变换的时频域范围内，说明NINO3.4 SSTA与SOI这两个ENSO指标对泉域地下水位的影响有其相似性。AO与水位动态在20世纪80年代中期至2005年左右存在显著的2～5a的周期，这应主要与地下水位的周期性有关(图4a3)。

连续小波变换可知，NINO3.4 SSTA、SOI与AO的周期主要表现在不同的多年时间尺度上。而以上三个指标与泉域降水、气温交叉小波变换的共振周期不明显，或仅存在1a尺度的共振周期(图4，b1～b3，c1～c3)。对于1a的共振周期，两序列的相位关系也不稳定。该共振周期的出现主要是受降水、气温1a周期性的影响，不能很好地反映气象指标多年尺度的周期性。应进一步通过小波相干谱分析识别泉域地下水位、降水、气温与气象模式的遥相关。

NPI的主周期为1a，与泉域地下水位、降水、气温交叉小波变换的周期也为1a，且显著时段分布连续，相位关系稳定，很好地反映了它们在波动强烈时段上的遥相关(图4a4～c4)。

4.3 小波相干谱分析

4.3.1 降水、气温与地下水位动态之间的小波相干谱分析

降水是济南泉域岩溶水资源的主要补给来源。在年际及多年周期尺度上，泉域地下水位动态与降水补给密切相关。对降水与地下水位进行小波相干谱变换，以分析二者的全时段共同变化特征，了解它们共同的波动周期及显著时段。同时，对气温与水位动态进行变换，分析二者的共同变化特征(图5)。

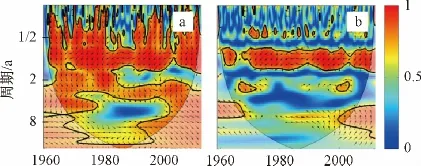
图5 降水(a)、气温(b)与地下水位动态的小波相干谱Fig.5 Wavelet coherence of(a)precipitation and(b)air temperature with respect to groundwater level dynamic

降水与地下水位动态的小波相干谱显示(图5a)，多数时频域上二者具有显著的共同变化，而能量密度大于0.5的区域更是涵盖了绝大部分时频域。降水是泉域地下水位波动的主要影响因素之一，对年际及多年变化更是如此，小波相干谱很好地展示了二者之间的这种密切相关的关系。1a左右和2～4a尺度的周期涵盖几乎全部1959—2011年的观测时段。在1a的周期尺度上，相位关系为降水领先于泉域地下水位动态3～4个月;2～4a周期为降水领先于水位动态约6～12个月。

气温与地下水位相干谱的显著时频域较降水明显减少(图5b)，说明它们共同变化的程度较降水与水位动态更低。气温与水位的主周期为1a，相位关系为气温领先于地下水位约3～4个月，与降水相位关系大体一致。需要说明，气温对济南泉域地下水位动态并不具有直接的影响，二者表现出的1a周期的共同变化，是因为泉域所处气候区为温带季风气候区，具有雨热同季的现象。因此，小波相干谱分析，包括交叉小波分析可揭示两个时间序列的共同变化，但两序列间是否具有因果关联，还是需要人为判定。

4.3.2 地下水位与大尺度气象指标的遥相关

为进一步分析泉域地下水位、降水、气温与大尺度气象模式的遥相关，将NINO3.4 SSTA、SOI、AO和NPI四个气象指标分别与泉域地下水位、降水、气温进行小波相干谱变换(图6)，以分析它们相互间全时段共同变化的时频域特征，了解其共同变化周期、显著时段及相位关系等信息。

泉域地下水位与NINO3.4 SSTA在1994—2011年存在6～14a的共振周期，相位关系为地下水位滞后NINO3.4 SSTA约2年(图6a1，表4)。该周期仅在九十年代位于COI区域外，周期代表性较弱。除6～14a的周期，二者其他周期的显著时段均很短，不具有代表性。泉域地下水位与SOI在1988—2011年具有7～13a的共振周期，周期尺度与NINO3.4 SSTA变换结果接近(图6a2)。相位关系为地下水位滞后于SOI约6年，明显大于地下水位对NINO3.4 SSTA的滞后时间。COI区域外显著时域为20世纪80年代后期至90年代。

图6 NINO3.4 SSTA(1)、SOI(2)、AO(3)和NPI(4)分别与地下水位(a)、降水(b)和气温(c)的小波相干谱Fig.6 Wavelet coherence of(1)NINO3.4 SSTA，(2)SOI，(3)AO and(4)NPI with respect to(a)groundwater level，(b)precipitation，and(c)air temperature

表4 地下水位、降水、气温与气象指标小波相干变换的周期性特征Tab.4 Periodicities of wavelet coherence transforms of groundwater levels，precipitation and air temperature with respect to climatic indexes

对比以上地下水位动态与ENSO两个指标的小波相干变换，可以发现两个变换在显著周期及分布时段上有很好的相似性，而小波相位角差别较大，表征的地下水位对两气象指标的滞后分别为约2年与约6年，这是由气象指标本身的周期差异所决定的。如前文所述，这两个指标各自反映的ENSO事件的时间尺度是不一致的，NINO3.4 SSTA主要反映2～6a的周期特征，而SOI主要反映9～14a的周期特征。

COI区域外，泉域地下水位与AO在1979—1994年存在4～7a的主共振周期，相位关系为地下水位动态滞后于AO约2年(图6a3)。水位与NPI的主共振周期为1a，相位关系为地下水位动态滞后于NPI约4个月(图6a4)。这一共振周期的显著时段涵盖了1959—2011年间的大多数观测时段，周期代表性好。此外，水位与NPI在1994—2002年存在约2a的周期，但显著时段短，代表性弱。

4.3.3 降水与大尺度气象指标的遥相关

泉域降水与NINO3.4 SSTA在1991—2011年存在6～12a的显著共振周期，相位关系为降水滞后于NINO3.4 SSTA大约9个月(图6b1，表4)。COI区域外显著时段为二十世纪九十年代至二十一世纪初。在1977—1985年存在4～5a周期，相位关系为降水滞后于NINO3.4 SSTA大约1年。泉域降水与 SOI在1976—1986年存在4～6a的共振周期，相位关系为降水滞后于SOI约3年，明显大于降水滞后于NINO3.4 SSTA动态的时间。在1997—2007年存在1～2a的共振周期，二者大约同相位分布(图6b2)。对比以上结果，降水与ENSO两指标的小波相干谱也是有其相似性的，二者主共振周期分布的时频域基本一致，差别主要为降水对两指标响应滞后时间的差异。与地下水位对ENSO两指标差异响应的原因一致，降水响应的时滞差异同样是由两气象指标本身所代表ENSO周期的尺度差异所引起的。

泉域降水与AO在1984—1989年存在2～4a的周期，此周期上二者呈反相位关系，表现为降水滞后于AO约1年时间(图6b3)。在1959—1965年存在1a左右的共振周期，二者基本呈同相位分布。COI区域外，降水与NPI存在显著的，在全部观测时段连续分布的约1a的共振周期，周期代表性极好(图6b4)。二者基本同相位分布，但降水稍有滞后，较NPI滞后约1个月。

4.3.4 气温与大尺度气象指标的遥相关

泉域气温与ENSO两指标NINO3.4 SSTA、SOI在COI区域外，共振周期的显著时段均很短，不具有代表性(图6c1-c2)。而气温与AO及NPI表现出了很好的共同变化。气温与AO在1982—2011年存在5～8a周期，相位关系为气温滞后于AO约5年，在1982年至二十一世纪初分布于COI区域外，具有显著的时频域特征(图6c3)。它们在全时段上均具有14～19a的周期，其中二十世纪七十年代末至九十年代初位于COI区域外，相位关系同样为气温滞后于AO约5年。此外，还可观察出2～3a与1a的周期，显著时段分别为1973—1979年与1959—1965年。

气温与NPI存在显著的，涵盖全部时域的1a的周期，该周期同地下水位及降水与NPI的主周期一致，此周期上气温与NPI呈同相位分布(图6c4)。在长周期尺度上，气温与SOI显著性类似，气温与NPI在全时域存在14～19a的周期，相位关系为气温滞后于NPI约5年。气温与NPI在1986—2011年存在6～10a周期，该时段上显著周期的尺度较气温与AO小波变换的周期尺度更长，后者为5～8a的周期。此外气温与NPI在1999—2011年存在2～3a周期也是显著的。

4.3.5 小波相干分析小结

泉域降水与地下水位1a与2～4a的周期在全时域显著相关，其他周期相关性也较好。气温与地下水位则主要在1a的周期上相关，基本在全时域显著。

以大尺度气象指标为主线对前文遥相关进行梳理，NINO3.4 SSTA与地下水位及降水主要在1～7a的周期尺度上存在遥相关;SOI与地下水位主要在6～13a及2～5a的周期上存在遥相关，与降水在4～6a的周期上存在遥相关;AO与地下水位及降水主要在1～7a尺度上存在遥相关，与气温主要在14～19a及5～8a周期上存在遥相关，在1～3a周期也有一定的遥相关性;NPI与地下水位、降水、气温的遥相关主要体现在1a的周期尺度上，与气温在14～19a与6～10a周期上也存在遥相关。上述遥相关的显著时域为，1a的周期基本在全时域显著，2～7a与14～19a的周期主要在20世纪80年代显著，6～14a的周期主要在20世纪80-90年代显著。

5 讨论

5.1 气象指标的尺度效应对遥相关性的影响

NINO3.4 SSTA、SOI、AO 及 NPI四个气象指标的影响尺度是不同的，前三个指标的影响范围大，像NINO3.4 SSTA与SOI，表征的是 ENSO现象，对全球范围的气候都会产生影响。而NPI影响范围相对较小，主要为北太平洋地区。由气象指标与地下水位、降水、气温的小波相干谱可直观地观察到，对济南泉域地下水位等而言，区域性气象指标NPI对它们的影响要更为直接，所表现出的遥相关也更为强烈。在1a的周期尺度上，NPI与地下水位、降水、气温均表现出了几乎涵盖全部观测时段的显著遥相关关系，这是其他三个指标未能展现的。其他指标与地下水位等的显著遥相关仅能涵盖某一特定的观测时段。说明济南岩溶泉域与区域性气象指标 NPI的遥相关性较 NINO3.4 SSTA等全球尺度指标更为显著。

5.2 关于小波变换响应时滞的讨论

前文中已分别进行了泉域降水与地下水位、气象指标与地下水位、气象指标与降水的小波相干谱分析，得出不同的响应时滞，这三个时滞之间应该有较好的对应关系。参照前文，就NPI指标，在1a周期尺度上，地下水位滞后于降水3～4个月，地下水位滞后于NPI约4个月，降水滞后于NPI约1个月，这三组小波相干分析结果的对应关系很好。对于NINO3.4SSTA与地下水位，在6～14a的周期尺度上，地下水位滞后于降水约1年，地下水位滞后于NINO3.4 SSTA约2年，降水滞后于NINO3.4 SSTA约9个月，这三组的对应关系稍差。这应当与显著周期的差异有关，地下水位与降水及地下水位与NINO3.4 SSTA的显著周期均为6～14a，而降水与 NINO3.4 SSTA的显著周期为6～12a。同时，对小波变换响应时滞的判读也会存在一定的误差。

6 结论

济南岩溶泉域地下水位、降水、气温的周期变化与NINO3.4 SSTA、SOI、AO及NPI等大尺度气象模式的周期变化存在遥相关，这种遥相关存在的认识与相关研究［13，15］的认识一致。大尺度气象模式并不直接对泉域地下水位产生影响，而是通过对降水等的影响间接产生影响，从而使二者表现出一定程度的遥相关。

岩溶泉域地下水位、降水、气温与大尺度气象模式遥相关的时频域及时滞是不同的。济南泉域地下水位1a的周期主要与NPI有关，在全观测时段遥相关显著;4～7a的周期主要与AO有关，在20世纪80-90年代中期遥相关显著;6～14a的周期主要与ENSO的两指标NINO3.4 SSTA、SOI有关，在20世纪80年代末至21世纪初显著。泉域降水1a的周期主要与NPI有关，全时段显著;2～4a周期主要与AO有关，在20世纪80年代后期显著;4～6a周期与6～10a周期均主要与NINO3.4 SSTA、SOI有关，分别在20世纪70年代中期至80年代中期以及90年代至21世纪初显著。泉域气温1a的周期主要与NPI有关，全时段显著;2～3a的周期主要与AO、NPI有关，分别在20世纪70年代及21世纪显著;5～10a的周期主要与AO、NPI有关，在20世纪80年代之后显著;14～19a的周期与AO、NPI有关，在20世纪70年代末至90年代显著。

本文主要采用统计学的方法对岩溶泉域地下水位、降水、气温与大尺度气象模式的遥相关进行了分析。在水文地质领域，进一步可研究全球不同地下水系统的地下水位、水化学等与大尺度气象模式间的遥相关，以认识气象模式对地下水资源的影响特征，帮助完善地下水资源管理。另外，地下水位关系到地下水资源量及诸多地质环境问题，预警预测工作十分重要，准确性的要求也较高。利用地下水位、降水、气温等与大尺度气象模式存在的遥相关，可在地下水位预警预测模型中耦合大尺度气象指标，以帮助提高预警预测精度。

［1］ 朱党生，张建永，史晓新，等.城市饮用水水源地安全评价(Ⅱ):全国评价［J］.水利学报，2010，41(8):914-920.［ZHU D S，ZHANG J Y，SHI X X，et al.Security assessment of urban drinking water sourcesⅡ.Security assessment for cities in China［J］.Journal of Hydraulic Engineering，2010，41(8):914-920.(in Chinese)］

［2］ 周仰效.娘子关泉流量的时间序列叠加模型［J］.工程勘察，1986(4):31-34.［ZHOU Y X.Time series superposition model of discharge of Niangziguan spring［J］.Geotechnical Investigation ＆ Surveying，1986(4):31-34.(in Chinese)］

［3］ 张闻胜，王银堂.时间序列分解模型在水文要素中长期预报中的应用［J］.水文，2001，21(1):21-24.［ZHANG W S，WANG Y T.Application of the time series decomposable model inmedium and longterm hydrologic forecasting［J］.Journal of China Hydrology，2001，21(1):21-24.(in Chinese)］

［4］ DAVEY M K，BROOKSHAW A，INESON S.The probability of the impact of ENSO on precipitation and near-surface temperature ［J］. Climate Risk Management，2014(1):5-24.

［5］ 龚道溢，王绍武.近百年ENSO对全球陆地及中国降水的影响［J］.科学通报，1999，44(3):315-320.［GONG D Y，WANG S W.ENSO influences on precipitation of global land and China in the past century［J］.Chinese Science Bulletin，1999，44(3):315-320.(in Chinese)］

［6］ 许武成，马劲松，王文.关于ENSO事件及其对中国气候影响研究的综述［J］.气象科学，2005，25(2):212-220.［XU W C，MA J S，WANG W.A review of studies on the influence of ENSO events on the climate in China［J］.Scientia Meteorologica Sinica，2005，25(2):212-220.(in Chinese)］

［7］ FU G B，YU J J，YU X B，et al.Temporal variation of extreme rainfall events in China，1961-2009 ［J］.J Hydrol，2013，487:48-59.

［8］ 龚道溢.北极涛动对东亚夏季降水的预测意义［J］. 气象，2003，29(6):3-6.［GONG D Y.Arctic oscillation’s significance for predictionof east asian summer monsoon rainfall［J］.Meteorological Monthly，2003，29(6):3-6.(in Chinese)］

［9］ 王绍武，龚道溢.近百年来的ENSO事件及其强度［J］. 气象，1999，25(1):10-14.［WANG S W，GONG D Y.ENSO events and their intensity during the past century［J］.Meteorological Monthly，1999，25(1):10-14.(in Chinese)］

［10］ BONSAL B R，SHABBAR A，HIGUCHI K.Impacts of low frequency variability modes on Canadian winter temperature［J］.Int J Climatol，2001，21(1):95-108.

［11］ LUQUE-ESPINAR J A，CHICA-OLMO M，PARDOIGUZQUIZA E，et al．Influence of climatological cycles on hydraulic heads across a Spanish aquifer［J］.J Hydrol，2008，354(1/4):33-52.

［12］ HOLMAN I P，RIVAS-CASADO M，HOWDEN N J K，et al.Linking North Atlantic ocean-atmosphere teleconnection patterns and hydrogeological responses in temperate groundwatersystems ［J］. Hydrol Process，2009，23(21):3123-3126.

［13］ TREMBLAY L，LAROCQUE M，ANCTIL F，et al.Teleconnections and interannual variability in Canadian groundwater levels ［J］.J Hydrol，2011，410(3/4):178-188.

［14］ GURDAK J J，HANSON R T，MCMAHON P B，et al.Climate variability controls on unsaturated water and chemical movement，High Plains aquifer，USA［J］.Vadose Zone J，2007，6(3):533-547.

［15］ KUSS A J M G，J J.Groundwater level response in U.S.principal aquifers to ENSO，NAO，PDO，and AMO ［J］.J Hydrol，2014，519(B):1939-1952.

［16］ 桑燕芳，王中根，刘昌明.水文时间序列分析方法研究进展［J］.地理科学进展，2013，32(1):20-30.［SANG Y F，WANG Z G，LIU C M.Research progress on the time series analysis methods in hydrology［J］.Progress Ingeography，2013，32(1):20-30.(in Chinese)］

［17］ TORRENCE C，COMPO G P.A practical guide to wavelet analysis［J］.B Am Meteorol Soc，1998，79(1):61-78.

［18］ 祁晓凡，杨丽芝，韩晔，等.济南泉域地下水位动态及其对降水响应的交叉小波分析［J］.地球科学进展，2012，27(9):969-978.［QI X F，YANG L Z，HAN Y，et al.Cross wavelet analysis of groundwater level regimes and precipitation groundwater level regime in Ji’nan Spring Region［J］.Advances in Earth Science，2012，27(9):969-978.(in Chinese)］

［19］ 祁晓凡，蒋忠诚，罗为群.典型表层岩溶水系统降水量与泉流量的交叉小波分析［J］.地球与环境，2012，40(4):561-567.［QI X F，JIANG Z C，LUO W Q.Cross wavelet analysis of relationship between precipitation and spring discharge of a typical epikarst water system［J］.Earth and Environment，2012，40(4):561-567.(in Chinese)］

［20］ GRINSTED A， MOOREJC， JEVREJEVA S.Application of the cross wavelet transform and wavelet coherence to geophysical time series［J］.Nonlinear Proc Geoph，2004，11(5/6):561-566.

［21］ 杨丽芝，李壮，祁晓凡，等.济南城市地质调查报告［R］.济南:山东省地质调查院，2014.［YANG L Z，LI Z，QI X F，et al.Report of Jinan urban geological survey［R］.Jinan:Shandong Institute of Geological Survey，2014.(in Chinese)］

［22］ 李文鹏，郑跃军，郝爱兵.北京平原区地下水位预警初步研究［J］.地学前缘，2010，17(6):166-173.［LI W P，HAO Y J，HAO A B.A preliminary study of groundwater level pre-warning in Beijing Plain［J］.Earth Science Frontiers，2010，17(6):166-173(in Chinese)］

［23］ 沈晔，李海涛，黎涛，等.地下水位预测:集合卡尔曼滤波(EnKF)应用概述［J］.水文地质工程地质，2014，41(1):21-24.［SHEN Y，LI H T，LI T，etal. Groundwater levelforecast:overview of application of the Ensemble Kalman filter(EnKF)［J］.Hydrogeology ＆ Engineering Geology，2014，41(1):21-24.(in Chinese)］