一种改进的异步CDMA信号的盲解扩算法*

张花国，李　鑫

(电子科技大学 电子工程学院，四川 成都 611731)

一种改进的异步CDMA信号的盲解扩算法*

张花国，李鑫

(电子科技大学 电子工程学院，四川 成都 611731)

对异步码分多址(CDMA)信号的盲解扩进行研究，提出了基于迭代最小二乘投影算法的改进算法。首先将异步CDMA信号建模为带约束的同步CDMA信号模型，并对其进行特征分解。将带约束的同步CDMA信号投影到其信号子空间中，再采用迭代最小二乘投影算法(ILSP)估计扩频序列，并用最小均方误差接收机获得信息码序列的估计值。理论分析和仿真结果表明，提出的算法比原迭代最小二乘投影算法具有更好的估计性能。

异步码分多址信号；盲解扩；迭代最小二乘投影算法；信号子空间

0　引言

随着数字通信技术的迅速发展，CDMA系统由于具有多址通信、抗干扰能力强、保密性好、低截获率等特性，在军用和民用领域得到广泛的应用[1，2]，如：全球定位系统(GPS)、联合战术信息分布系统(JTIDS)、第3代CDMA通信系统等。对于合作方，由于事先已知扩频码，可以采用 RAKE接收[3，4]、多用户检测[5，6]等技术实现通信。但是对于非合作接收方，无法获得合作双方的扩频码序列。而要实现对截获信号的解扩，就需要事先对扩频码序列进行估计。因此，如何提取接收到的CDMA信号中的扩频序列和信息序列具有重要意义。

根据不同用户扩频序列时延的不同，CDMA信号可分为同步CDMA信号和异步CDMA信号。对于同步CDMA信号的盲解扩问题，Yao Yingwei等人[7]提出了基于 EM算法的CDMA信号盲估计；A.Haghighat等人[8]利用基于MUSIC(Multiple Signal Classification)算法对同步 CDMA信号进行盲解扩；Albataineh Z等人[9]将 H-DE(Hyper Differential Evolution)最优化技术应用到 CDMA信号的盲解扩中，并和 ICA(Independent Component Analysis)算法的性能进行了比较。而异步CDMA信号的盲解扩问题较同步 CDMA信号困难，相关的文献也较少。文献[10]针对异步CDMA信号提出了一种利用ILSP算法估计扩频码和信息码的方法。该方法将异步CDMA信号建模为带有约束条件的同步CDMA信号，通过循环迭代对扩频矩阵和信息矩阵进行估计。该算法的优势是其较低的运算复杂度，但在扩频序列未知的情况下，ILSP算法的盲解扩性能受限[11]。

由于ILSP算法存在的缺陷，本文在该算法的基础上，提出了一种改进的异步CDMA信号的盲解扩算法。和ILSP算法相比，本算法在几乎不增加运算复杂度的情况下，提升了扩频码盲估计的性能。理论分析和仿真结果验证了本文方法的有效性。

1　信号模型

假设接收端截获的信号为R个用户的异步CDMA信号，经过以码元速率采样后，可以用下式表示：

R个用户的异步CDMA信号模型可以由图1表示。

图1　异步CDMA信号模型

如图1所示，在不考虑噪声的情况下，接收端接收到的信号为 R个用户的信息码 br(r=1，2，…，R)经各自的扩频序列cr扩频后，经过一定的时延τr和衰减ar后相叠加的结果。

为了将接收到的序列y(n)建模为带约束的同步CDMA信号，可以将 y(n)重写为秩为 2R的 L×M维矩阵，即式(1)可写为如下的矩阵形式：

其中V为方差为σ2的L×M维高斯白噪声矩阵，C为扩频序列张成的L×2R维矩阵：

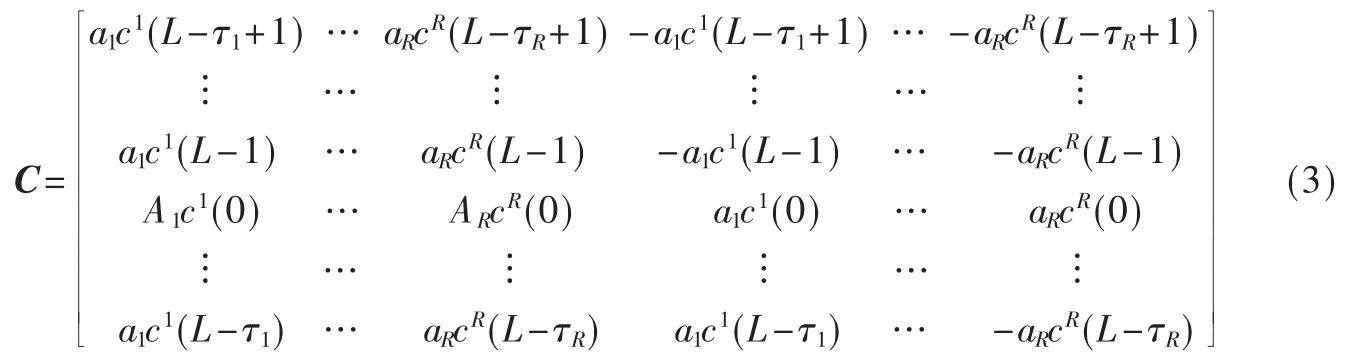
信息矩阵B满足以下约束条件：

(1)B为M×2R维矩阵，且每个元素取值为0或±1；

(2)对于 m=1，2，…，M和 r=1，2，…，R，Bm，r和 Bm，r+R仅有一个元素为 0，另一个元素为±1；

(3)对于r=1，2，…，R，有B1，r≠0；

(4)对于 m=2，3，…，M和 r=1，2，…，R，当且仅当Bm，r+Bm，r+R=Bm-1，r+Bm-1，r+R时有 Bm，i≠0。

2　改进ILSP算法

由式(2)可知，Ym的协方差矩阵可以表示为RY=E[Ym]，其中，Ym表示观测矩阵Y的第m列。对于RY，可由样本的协方差矩阵=YYH/M近似得到。对进行特征分解可得：

在H和B都未知的情况下，可以采用ILSP算法对投影后得到的矩阵X进行分解，从而得到H和B的估计值，即求得矩阵H和B满足如下条件[11]：

其中，||·||F表示矩阵的Frobenius范数。

利用ILSP算法[10]求解式(5)的计算步骤如下：

(1)t=0，随机初始化H(0)；

(2)t=t+1，计算 S=(H(t-1))†X，其中(·)†表示求伪逆操作；

(3)令 ZT=sign(S1:R，:+SR+1:2R，:)，并采用上面对信息矩阵B的约束条件将M×R维矩阵Z扩展为M×2R维矩阵B(t)，Si，j，:表示矩阵 S的第i到第j行的所有列；

(4)计算 H(t)=X(B(t))†；

(5)运行步骤(2)、(3)和(4)直至收敛或者达到最大迭代次数。

因此，随机初始化H(0)经过以上算法循环迭代后，即可得到矩阵H和信息矩阵B的估计值、。由H=C可知，扩频矩阵C的估计值可以通过下式得到：

利用得到的扩频矩阵估计时延，构建MMSE接收机[15]，可以得到信息矩阵 B的估计值。

当扩频增益 L＞2R时(如式(5)所示)，将观测矩阵 Y投影到信号子空间上再利用ILSP算法求解，虽然会稍微降低迭代的收敛速度，但投影之后观测矩阵的维度由L×M降为2R×M，大大减少ILSP算法中每次迭代的计算量，并且可以起到去噪的作用，使算法具有更好的估计性能。

3　仿真结果

为了验证本文提出的算法的有效性，进行了两个仿真实验，针对不同信噪比和信号样本长度，对本文提出的改进算法、ILSP算法进行仿真，并和已知扩频波形的合作通信的解扩性能进行比较。

实验1不同信噪比下的解扩性能比较

假设用户数R=3，信号样本长度为M=50，且扩频增益为L=31，进行1 000次蒙特卡罗实验得到不同信噪比下ILSP算法和本文提出算法的误码率，并与合作通信进行比较。实验结果如图2、图3和表1所示。

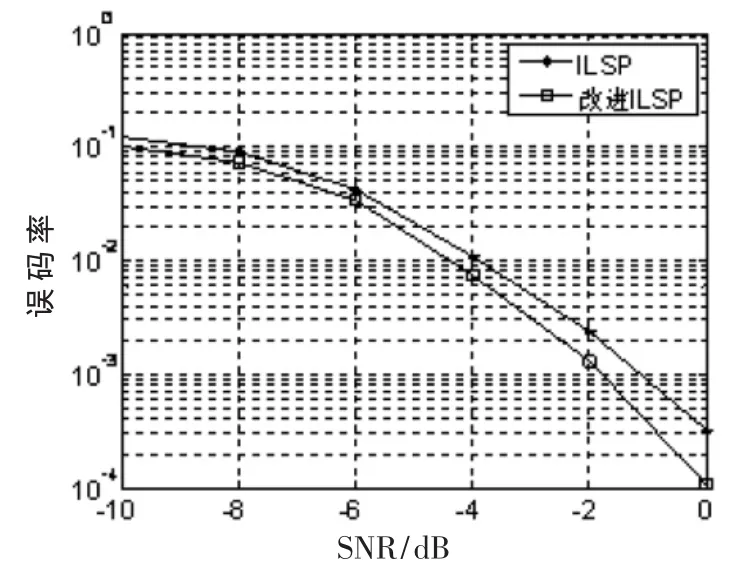
图2　扩频码误码率随信噪比变化曲线

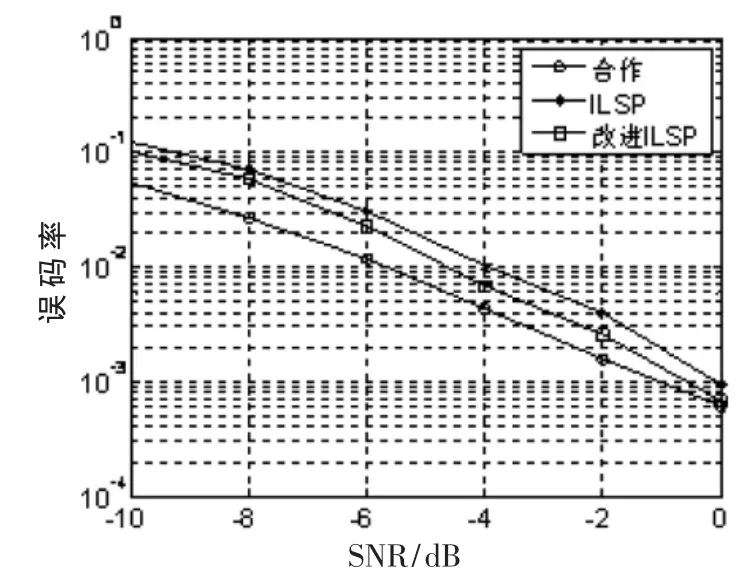
图3　信息码误码率随信噪比变化曲线

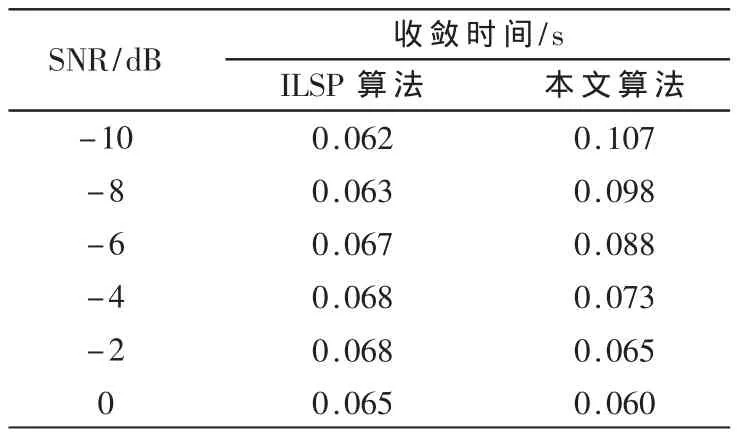
表1　不同信噪比下算法平均收敛时间

实验2不同信号样本长度下的解扩性能比较

假设用户数R=3，扩频增益为L=31，在信噪比SNR=-6 dB的条件下，针对不同的信号样本长度 M进行1 000次蒙特卡罗实验得到 ILSP算法和本文提出的算法的误码率，并与合作通信进行比较。实验结果如图4、图5和表2所示。

图4　扩频码误码率随样本长度变化曲线

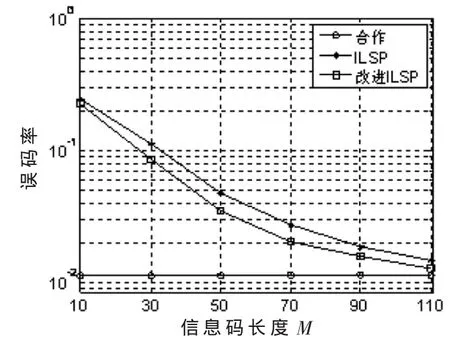
图5　信息码误码率随样本长度变化曲线

表2　不同信息码长度下算法平均收敛时间

实验1和实验2的结果表明，采用ILSP算法和本文提出的改进算法实现信号盲解扩的估计性能都随着信噪比和信号样本长度的增加而逐渐提高，并逐渐逼近合作通信的效果，且本文提出的改进算法比ILSP算法具有更好的估计性能。虽然在信噪比较低或信号样本长度较短时，本文提出的改进算法的收敛速度较ILSP算法稍慢一些，但随着信噪比的增加或信号样本长度的增长，改进算法的收敛速度逐渐接近并优于ILSP算法。这说明本文提出的估计算法是一种有效的估计。

4　结论

本文对异步CDMA信号的盲解扩问题进行研究。首先，构建了异步CDMA的信号模型，将异步CDMA信号建模为带有约束条件的同步 CDMA信号。随后，在ILSP算法的基础上，提出了一种改进的算法。该算法在几乎没有增加计算复杂度的同时，提升了算法的估计性能。仿真结果验证了本文提出的方法的有效性。

[1]FLIKKEMA P.Spread-spectrum techniques for wireless communication[J].Signal Processing Magazine，IEEE，1997，14(3)：26-36.

[2]GOLDSMITH A.Wireless Communications[M].Cambridge：Cambridge University Press，2005.

[3]WASDEN D L，MORADI H，FARHANG-BOROUJENY B. Comparison of direct sequence spread spectrum rake receiver with a maximum ratio combining multicarrier spread spectrum receiver[J].Communications，IEEE International Conference on，2014：4656-4661.

[4]KHAIRNAR V，MATHUR J，SINGH H.Design and perfor mance analysis of DS-CDMA rake receivier for wireless communication[C].Electronics and Communication Systems (ICECS)，2014 International Conference on.IEEE，2014：1-6.

[5]de Almeida A L F，Fernandes C A R，Benevides da Costa D.Multiuser detection for uplink DS-CDMA amplify-andforward relaying systems[J].IEEE Signal Processing Letters，2013，20(7)：697-700.

[6]KURNIAWAN A.Effect of power imbalance on multiuser detection of DS-CDMA systems[C].Electrical Engineering and Computer Science(ICEECS)，2014 International Conference on.IEEE，2014：235-239.

[7]YAO Y，POOR H V.Eavesdropping in the synchronous CDMA channel：an EM-based approach[J].Signal Processing，IEEE Transactions on，2001，49(8)：1748-1756.

[8]AFSHIN H，Reza Soleymani M.A music-based algorithm for blind user identification in multiuser DS-CDMA[J]. EURASIP Journal on Advances in Signal Processing，2005 (5)：649-657.

[9]ALBATAINEH Z，SALEM F.New blind multiuser detection in DS-CDMA using H-DE and ICA algorithms[J].Intelligent Systems Modelling&Simulation(ISMS)，2013 4th International Conference on，2013：569-574.

[10]AVITZOUR D.Detection of asynchronous CDMA with unknown user waveforms[J].Signal Processing Letters，IEEE，2004，11(2)：209-211.

[11]VIBERG T S.Blind separation of synchronous co-channel digital signals using an antenna array[J].Signal Processing，IEEE Transactions on，1996(5)：1184-1197.

[12]TSATSANIS M K，GIANNAKIS G B.Blind estimation of direct sequence spread spectrum signals in multipath[J]. IEEE Transactions on Signal Processing，1997，45(5)：1241-1252.

[13]BUREL G.Detection of spread spectrum transmissions using fluctuations of correlation estimators[C].IEEE ISPACA，2000.

[14]董占奇，胡捍英，于宏毅.基于延迟相乘-相关及谱分析的直扩信号检测与符号周期、码片时宽估计分析[J].电子与信息学报，2008，30(4)：840-842.

[15]HONIG M，TSATSANIS M K.Adaptive techniques for multiuser CDMA receivers[J].Signal Processing Magazine，IEEE，2000，17(3)：49-61.

An improved approach to blind despreading of the asynchronous CDMA signal

Zhang Huaguo，Li Xin
(School of Electronic Engineering，University of Electronic Science and Technology of China,Chengdu 611731,China)

In this paper,we proposed an improved algorithm based on the iterative least squares with projection(ILSP)algorithm to solve the problem of the blind dispreading of asynchronous code division multi-access(CDMA)signal.Firstly，the asynchronous CDMA signal was modeled as the synchronous CDMA signal with constraints.Then the eigen-decomposition method was employed to the new signal model.The ILSP algorithm was used to estimate the spread spectrum sequence after the synchronous CDMA signal with constraints was projected to its signal subspace.In the end,an MMSE receiver was implemented to obtain the estimation of the information sequence.The theoretic analysis and experimental results show that the performance of the improved algorithm is better than the ILSP algorithm.

asynchronous CDMA signal；blind dispreading；ILSP algorithm；signal subspace

TN911.7

A

10.16157/j.issn.0258-7998.2015.10.021

国家自然科学基金(61201282)，中央高校基本科研业务费（ZYGX2013J016）

（2015-05-24）

张花国（1979-），男，博士，副教授，主要研究方向：复杂通信信号截获与分析。

李鑫（1991-），男，硕士研究生，主要研究方向：非合作信号处理。

中文引用格式：张花国，李鑫.一种改进的异步 CDMA信号的盲解扩算法[J].电子技术应用，2015，41(10)：77-80.

英文引用格式：Zhang Huaguo，Li Xin.An improved approach to blind despreading of the asynchronous CDMA signal[J].Application of Electronic Technique，2015，41(10)：77-80.