输入饱和约束下一类多智能体编队系统鲁棒一致性分析

周绍磊，闫 实，刘 伟，李瑞涛

（中国人民解放军海军航空工程学院 控制工程系，山东 烟台 264001）

输入饱和约束下一类多智能体编队系统鲁棒一致性分析

周绍磊，闫 实，刘 伟，李瑞涛

（中国人民解放军海军航空工程学院 控制工程系，山东 烟台 264001）

针对输入饱和约束条件下具有不对称时滞的二阶多智能体编队系统的鲁棒一致性问题，本文综合利用Lyapunov-Krasovskii泛函方法和线性矩阵不等式的方法对其进行了研究。首先在n维欧氏空间中建立了二阶多智能体所组成的编队系统的数学模型；然后设计了分布式的基于一致性的具有饱和约束和不对称时滞的编队控制律；进一步，利用非线性扇区法处理了饱和项，将其转化为一种简单的非线性项，从而建立了Lyapunov-Krasovskii泛函，并利用LMI方法对编队系统进行了鲁棒一致性分析，得到了系统达到鲁棒一致时的线性矩阵不等式条件，并通过仿真分析验证了所得条件的正确性。

输入饱和；时滞；鲁棒一致性；编队控制

编队控制是智能群体自主协同控制中最为基础的一项技术，在军事、航天、工业、生活等各个领域有着广泛的应用前景。所谓编队控制，是指由多个智能体组成的群体向某一特定目标运动的过程中，相互之间保持预定的几何形态（即队形），同时又要适应环境约束（如避障）的控制问题。

近年来，基于一致性的编队控制理论受到了广泛关注。所谓一致性（有些也称为“趋同性”），就是指多智能体系统中的每个个体通过相互之间的信息交互，最终在各项协同变量（如，位置、速度、能量等）上趋于一致。

在实际的控制系统中，控制器通过执行器来驱动受控对象，而环境或者系统自身的物理结构决定着执行器的输出量及其变化率不能任意大，因而执行器一般都存在幅值饱和约束问题。而编队控制输入（队形、速度、过载等）往往也是有着严格约束的，目前基于分布式多智能体系统的饱和约束问题的研究目前还比较少。

本文综合考虑输入饱和受限条件下，对同时具有不对称时滞以及通讯噪声的情况下的多智能体编队的鲁棒一致性问题进行分析。利用Lyapunov稳定性理论以及线性矩阵不等式方法（LMI方法）得到了多智能体编队达到鲁棒一致的充分条件。

1 问题描述

1.1 具有输入饱和约束和外界扰动的多智能体编队系统

考虑n维欧氏空间中一个由N个具有输入饱和约束和外界干扰的二阶智能体组成的编队系统，其中第i个智能体的动力学方程由下式描述：

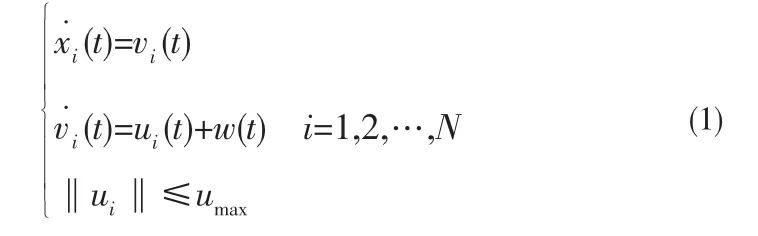
其中，xi(t)∈Rn，vi(t)∈Rn，ui(t)∈Rn分别表示n维欧氏空间中智能的位置向量、速度向量和控制输入向量；umax∈R为常值,表示控制输入幅值约束；w(t)∈L2[0,∞)为系统有界干扰。

无向图G=(V,E,A)表示智能体间的通讯拓扑结构，其中V={V1,V2,…，Vn}为节点集合，也可用其下标代指。E⊆V×V为边集合，A=[aij]，∀i，j=1,…,n为邻接矩阵，用于描述系统的通信拓扑结构。如果(i,j)是G图的一条边，表示智能体j和i可以交换信息，记aij=1。L=[LT1LT2…LTN]为拉普拉斯矩阵，且有以下形式：

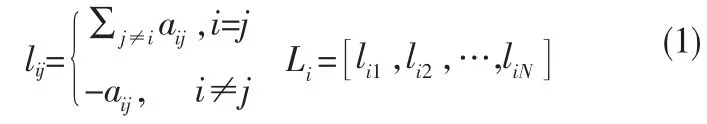
编队队形是智能体在空间中建立并能保持的一种特定的几何位置关系。描述编队队形的方法有多种[1-3]。很多情况下，分布式控制系统中的单个智能体很难知道自身的绝对位置，因而从实际出发，本文采用基于相对位置向量的方法描述队形，其具体描述方式下：

定义1基于相对位置向量的队形描述方法

n维欧氏空间中，智能体i和智能体j之间理想的位置偏差向量为hij∈Rn，i=1,2,3,…,N。其中向量hi∈Rn，i=1,2,3,…,N表示智能体i在空间中期望的位置，则，hij=hi-hj，∀i,j= 1,2,3,…,N。编队向量为，其中Ni表示当前时刻智能体i的邻居个数，则编队向量与编队队形是一一对应的。

为验证所设计的控制协议能够使得编队系统达到一致且对外界干扰具有良好的抑制能力，引入了性能输出变量zi(t)由下式给出：

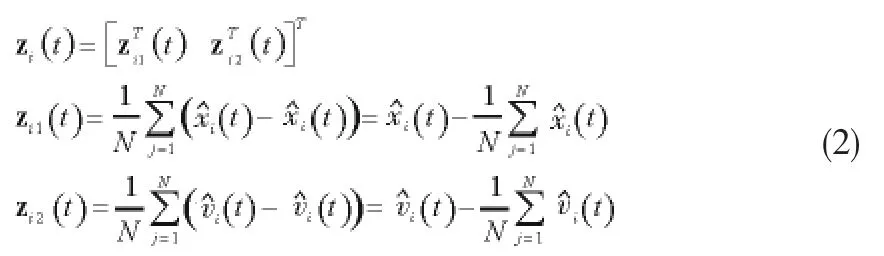
进一步，令z(t)=[z1(t)，z2(t),…,Zn(t)]T

其中，

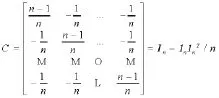
注意到对于矩阵C=In-1n1nT/n，0是其特征值，重数为1；1是其特征值，重数为n-1；向量inT、1n分别是特征值0的左右特征向量且有CTC=C。

定义2系统 EE（Energy-to-Energy）增益指标

‖Twz‖ee越小，表明外界扰动对系统的影响越小，因此反映了系统抑制外部扰动的能力。

定义3编队系统的次优H∞一致性

对于给定的多智能体编队系统（1）以及和可实现的性能指标γ＞0，如果

1）当wi(t)=0时，编队能够形成并保持，即对于任意的智能体i和智能体j，如果存在某一有界时刻t0，当t≥t0时，等式xi(t)-xj(t)=hij和vi(t)=vj(t)=vd始终同时成立，则称编队形成并保持，其中vd是智能体期望的速度。

2）当wi(t)≠0时，‖Twz‖ee＜γ，则控制律ui为γ次优一致性鲁棒H∞编队控制律。那么编队系统实现了次优H∞一致性。

1.2 基于一致性的编队控制律设计

假定编队的位置通讯拓扑与速度通讯拓扑是相同的。文献[4]给出了编队控制中经典的静态一致性算法（3），该算法已经被验证能够使得编队中的所有个体达到同一位置：

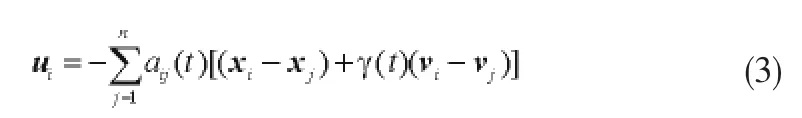
在实际系统中不仅存在着输入饱和现象，还存在着时滞现象。时滞往往降低了系统的稳定性及其他性能。记τij(t)为t时刻，智能个体j从它的邻居i接受信息时的通信时滞。关于通讯时滞我们规定以下两点假设：

假设1通讯网络中仅存在不对称时滞。智能体获取自身状态信息没有时滞，即τij(t)=0；时滞仅存在于智能体获取邻居状态信息时，即0＜τij(t)＜τ。

假设2多智能体编队系统中的通讯时滞是均等的。即对任意的智能体i、j、k均有等式τij(t)=τkj(t)=τjk(t)=τ(t)成立。如果系统内的通信时滞满足τ(t)=τ＞0，τ˙(t)=0，则该时滞为恒定均等时滞；如果τ＞0，τ˙(t)＞0为常数，则该时滞为时变均等时滞。

这两点假设是具有实际意义的。在通讯网络中智能体检测自身状态信息的时间相对于检测邻居状态信息的时间往往是可以忽略不计的；同时，在通讯网络协议中可以引入时间队列机制，即在规定的时刻点，所有个体统一进行信息更新，这样做会一定程度上避免出现异步通讯，同时也可以近似认为出现了均等通讯时滞。

在经典的静态一致性算法的基础上，设计了新的具有不对称时滞的动态一致性算法（4）：

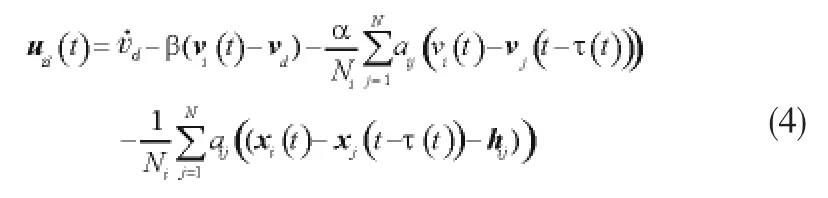
其中，xj(t-τ)),vj(t-τ(t))∈Rn分别为具有通信时滞τ(t)的个体j的位置和速度向量；uid(t)∈Rn为个体i的控制输入向量；vd∈Rn，∈Rn表示期望的编队速度和编队加速度；α＞0，β＞0为有界控制参数；hij是个体i，j的期望相对距离向量；N为智能群体内个体的个数，Ni是个体i当前时刻的邻居个数。

定义4非线性饱和函数

非线性饱和函数记为sat(·)，当y∈R时sat(y)=sign(zi)min

当y=(y1,y2,…,yn)T∈Rn时，非线性饱和函数可以写成向量形式，sat(y)=(sat(y1),sat(y2),…,sat(yn))T

则输入饱和约束下的具有不对称时滞的一致性编队控制律为：

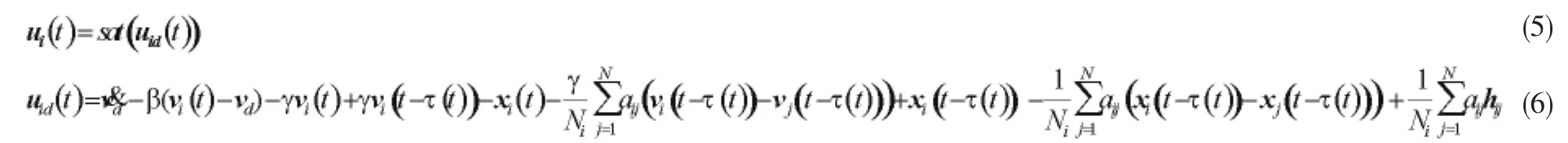
利用Kroneck积的形式得到编队系统在输入饱和约束下的一致性编队控制律为u(t)：uds(t)=sat(ud(t))

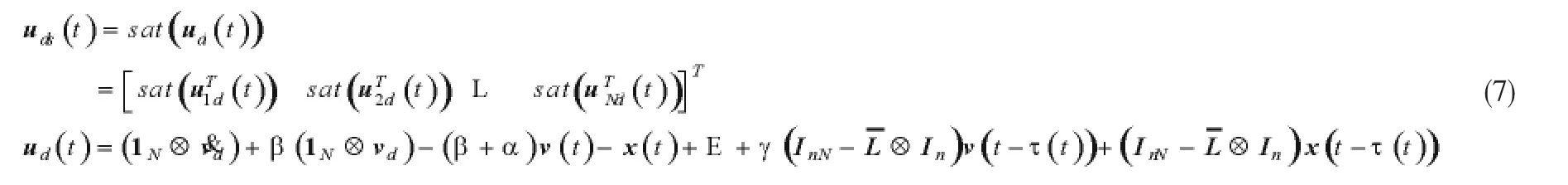
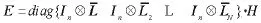
1.3 预备引理

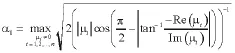
引理1[5]不存在控制输入约束、外界干扰、时滞等情况下，若编队速度vd和期望的编队向量h是精确已知的，控制系数α＞α0，β＞0且有界，则当系统通信拓扑强连通且存在最小有向生成树时，系统（1）是稳定的。其中，

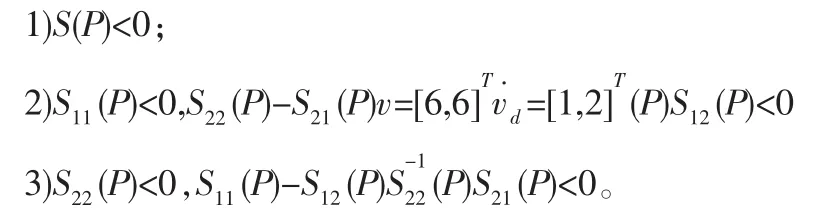
2 系统稳定性分析

2.1 系统的等价代数变换

为方便进行数学推导，首先要对系统进行代数等价变换。令：

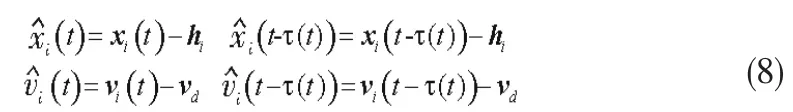
将含不均等时滞的编队控制律 (4)等价变换并利用Kroneck积的形式整理得智能群体的不对称时滞编队控制律(9)

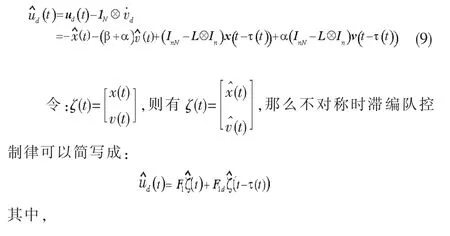
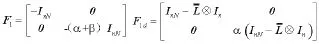
2.2 基于非线性扇区法的饱和项处理

考虑到饱和函数的非线性特性，直接运用Lyapunov第二方法分析系统的稳定性较为困难。 而将饱和函数建模成一个满足扇形条件的普通非线性模型是一个常用的方法[6]。因为

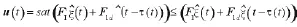
不妨设：

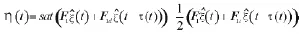
则有：

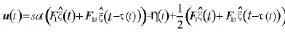
由此，我们可以得到闭环状态方程：

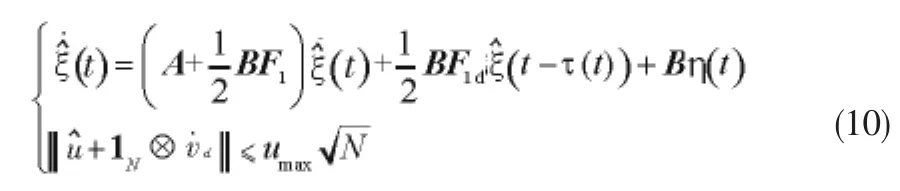
2.3 基于Lyapunov-K rasovskii泛函方法与LM I方法的编

队稳定性分析与鲁棒性分析

定理1：输入饱和约束下考虑存在外界干扰和不对称均等时滞的满足引理1的多智能体编队编队系统。如果存在对称正定矩阵P∈R2nN×2nN，Q∈R2nN×2nN使得Γ＜0，则智能群体系统编队能够实现次优H∞一致性，干扰抑制度γ，其中：

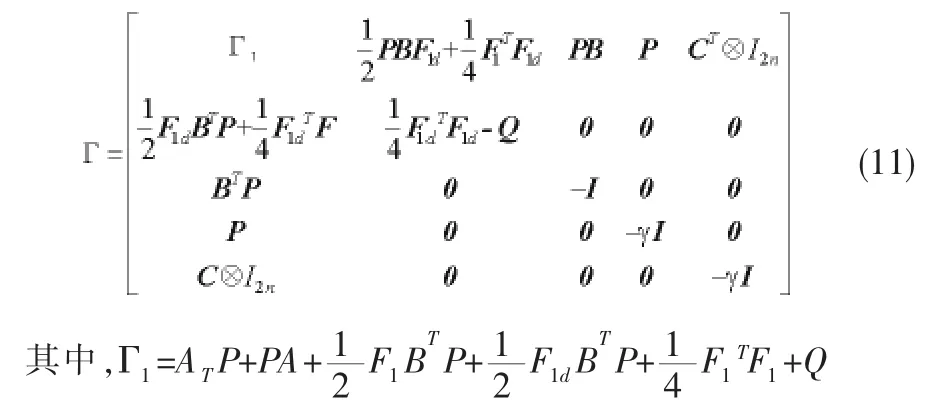
证明：

1）首先讨论系统的镇定问题，构造Lyapunov-Krasovskii泛函为如下形式：

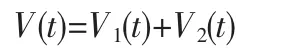
其中，

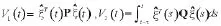
则有：

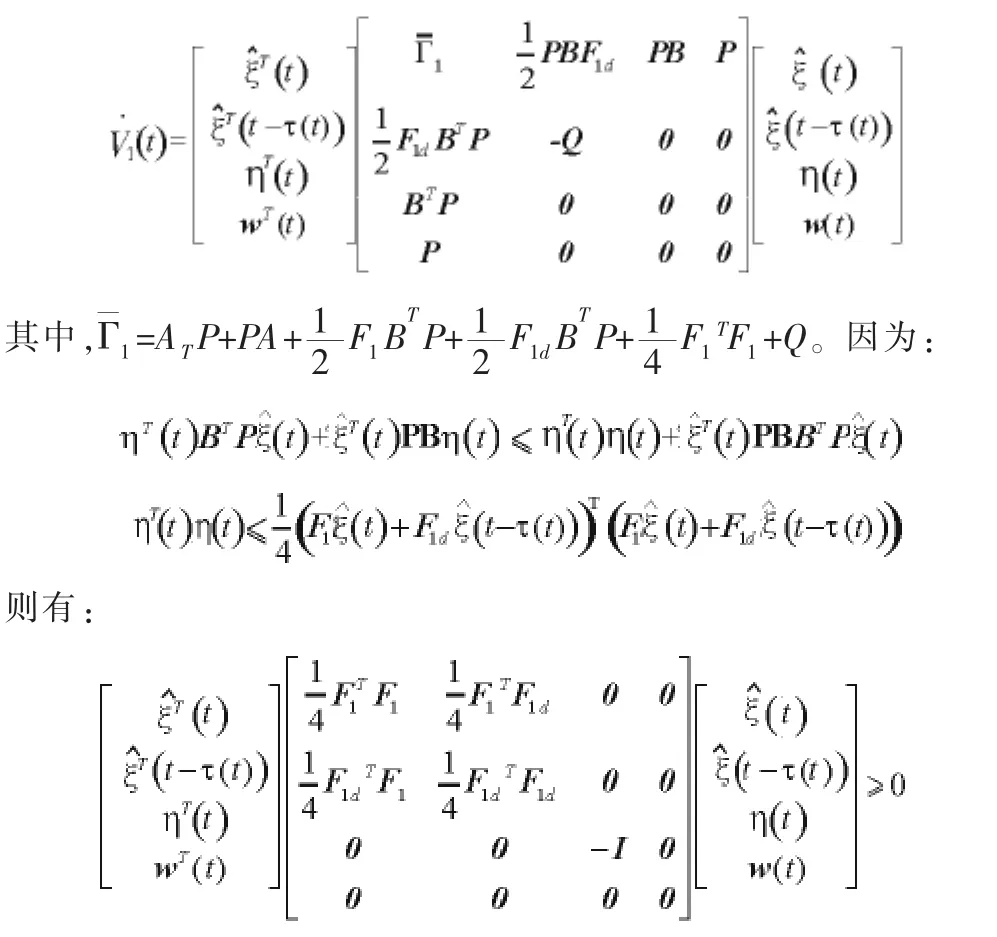
根据定义3，首先考虑当w(t)=0时的编队闭环系统的镇定问题，若以下不等式成立：

由此可知，当定理1中LMI（11）成立时，

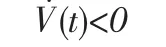
根据定义3，编队形成并保持等价于下列等式同时成立：

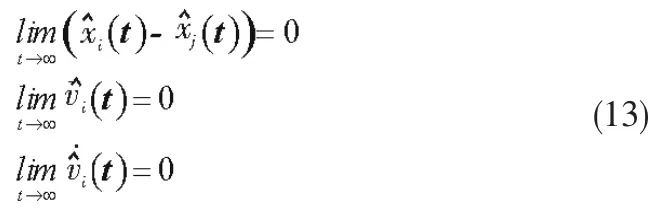
因此，由lyapunov稳定性理论可知，当V(t)正定，且其沿着轨线的倒数V˙(t)负定时，闭环编队系统（10）的输出解是一致渐进稳定的，因而满足等式（13）的要求，所以编队可以形成并保持。

2）其次讨论编队系统（10）的问题。

结合定义2中的EE（Energy-to-Energy）增益指标‖Twz‖ee的形式，定义如下H∞的性能指标：

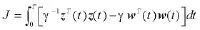
其中，T＞0，w(t)∈L2[0,∞)为系统有界干扰。

记为：

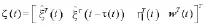
并且利用矩阵C=In-1n1n/n的性质，可得：

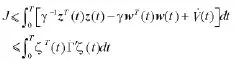
其中：

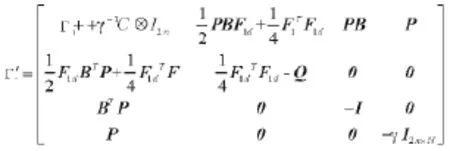
由引理2,矩阵的schur补性质可知：

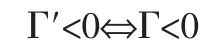
所以，当Γ＜0时，以下不等式成立：

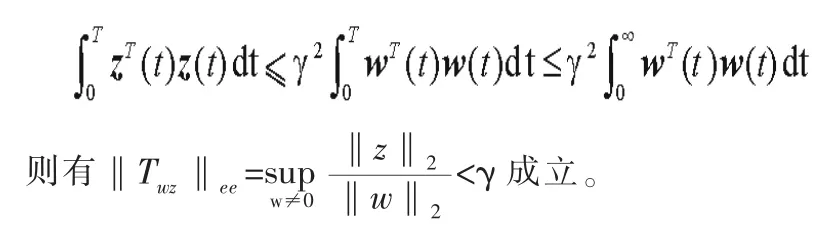
证毕。

3 仿真验证

在不对称均等时滞下，研究包含3个智能个体的群体系统在平面内编队运动的情况。每个智能个体动态方程均为二阶模型。个体的初始位置随机分布在[0,60]×[0,60]的范围内，初始速度向量均为0；通信连接拓扑结构如图1所示，期望的编队向量是hT，h=[0,-100,100,0,100,100,100,0,200,-100,0,0,-100,-200,0,-100,0,0];

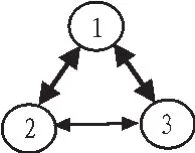
图1 编队通讯拓扑Fig.1 Fleet communication topology

期望的初始编队速度为v=[6,6]T，编队加速度=[1,2]T；控制参数；仿真时间40 s，仿真步长0.1 s。根据通信拓扑结构图1，可以得到编队系统的邻接矩阵、度矩阵和归一化拉普拉斯矩阵为：

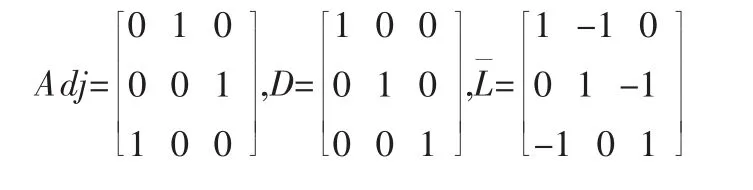
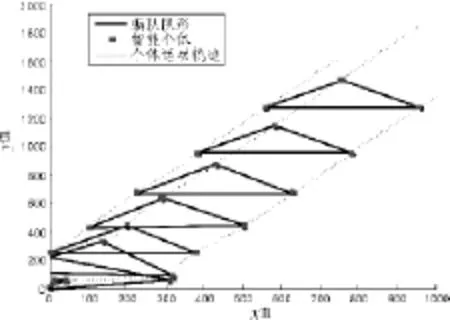
图2 编队队形与运动轨迹Fig.2 The motion path of the group

给定系统时滞为0.36将个体的控制输入约束限定为umax=50，继续在系统中引入随机分布在区间[0,10]内的噪声，使用MATLAB的LMI工具箱求解线性矩阵不等式，存在可行解。则同时存在输入约束、时滞和噪声的情况下，仿真结果如图3所示。

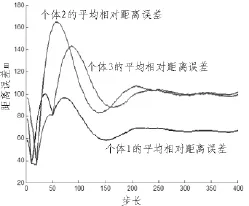
图3 编队位置误差变化情况Fig.3 The formation error of the fleet

通过图2可以看出期望的编队队形基本可以形成并保持。图3表明个体间的期望相对距误差并未收敛到零，而是收敛到恒定值，说明了基本队形形成并保持；图4表明描述了个体速度和期望编队速度编队的变化，个体速度达成一致，但是受到时滞和噪声的影响，个体速度与编队速度之间存在较小的偏差并未收敛到编队速度。

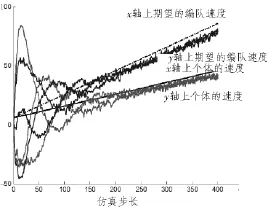
图4 编队速度误差变化情况Fig.4 The velocity error of the fleet

4 结论

文中结合实际情况，设计了输入饱和约束情况下，存在不对称时滞与外界干扰条件时的多智能体系统编队控制律。通过理论推导得到了编队系统达到鲁棒一致的LMIs条件，仿真结果证明了结论的正确性。

[1]Olfati-Saber R,Murray R M.Distributed structural stabilization and tracking for formations of dynamic multi-agents[C]//Proceedings of the 41st IEEE Conference on Decision and Control,Las Vegas,Neveda,USA,2002.

[2]Wang P K C.Navigation strategies for multiple autonomous mobile robots moving in formation[J].Journal of Robotic Systems,1991,8(2)：177-195.

[3]REN W.Consensus for cooperative of vehicle formations[J].I ET Control Theory and Applications,2007,1(2):505-512.

[4]REN W.Distributed Consensus in Multi-vehicle Cooperative Control[M].Utah State:Spring,2007.

[5]CHEN B S, WANG S S.The stability of feedback control with nonlinear saturating actuator[J].IEEE Trans on Auto Control,1998,33(5):483-487.

[6]苏宏业,潘红华.一类具有非线性饱和执行器的不确定时滞系统鲁棒控制[J].控制与决策,2001(15):23-26.SU Hong-ye,PAN Hong-hua.Robust control or a class of uncertain time-delay systems containing nonlinear saturating actuator[J].Control and Decision,2001(15):23-26.

Robust consensus analysis for a class of multi-agent group formation w ith input saturation constraints

ZHOU Shao-lei，YAN Shi，LIU Wei，LI Rui-tao
（Department of Control Engineering，Naval Aeronautical and Astronautical University,Yantai 264001，China）

In this paper,we research the robust consensus problems for a second-order Multi-Agent group formation with input saturation constraints and asymmetric delays using the Lyapunov-Krasovskii factional method and the LMI method.The double-integrator dynamical model with input saturation constraints is established in the n-dimensional Euclidean space.Then,according to the superposition principle the distributed consensus control algorithm for the model is designed.Further, the nonlinear sector method is used to deal with the saturated elements,then the Lyapunov-Krasovskii factional is established, then the LMI method is used to analysis the robust consensus of the formation systems.After that the LMIs conditions when the formation system is robust consensus.In the last,the simulation proves the correctness of these idea.

input Saturation Constraints;delay;robust consensus;formation control

V21

A

1674－6236（2015）10-0125-05

2014-08-26 稿件编号：201408151

国家自然科学基金（61273058）

周绍磊(1963—)，男，山东泰安人，博士，教授。研究方向：智能导弹协同控制。