基于卡尔曼滤波-神经网络预测的GNSS/INS误差反馈校正的研究

张静娴，杨英东，钱 峰

（上海交通大学 电子信息与电气工程学院 导航与控制研究所，上海200240）

基于卡尔曼滤波-神经网络预测的GNSS/INS误差反馈校正的研究

张静娴，杨英东，钱 峰

（上海交通大学 电子信息与电气工程学院 导航与控制研究所，上海200240）

当GNSS信号失锁时，GNSS/INS组合导航系统的误差会随着时间而积聚从而失去导航的功能。通过理论分析和数学建模，本文提出了一种基于卡尔曼滤波-RBF神经网络预测INS误差并进行补偿，从而弥补GNSS失锁无法导航的缺陷。卡尔曼滤波器为神经网络的训练提供了数据预处理的作用。通过跑车实验和仿真，最后证实了方法的可行性，在平均位置误差为3米的情况下，能够持续30秒左右的精准预测。

卡尔曼滤波；神经网络；全球导航卫星系统；捷联惯性导航系统

近年来，各国一直在研究全球导航卫星系统（GNSS），旨在应用于工业、军事和民用产业。目前，GNSS包含了美国的GPS、俄罗斯的 GLONASS、中国的 Compass(北斗)、欧盟的Galileo系统，可用的卫星数目达到100颗以上。GNSS由三个部分组成：卫星星座、地面监控、地面接收设备。卫星导航系统利用绕地运行的多颗卫星，为地面上的用户提供了连续实时的导航服务与高精度的授时服务，用户可以随时获取当前时刻的地理位置和速度信息，卫星导航具有定位精度高、系统成本低的特点。

但是由于高动态环境会削弱接收机对信号能力的捕捉和跟踪，甚至会短时间内丢失卫星信号影响到正常导航；山脉、高楼、树木的遮挡也会致使GNSS接收机接收卫星信号变差，无法达到定位要求；或者由于遮挡产生多路径效应，造成很大的定位偏差等。

惯性导航系统（INS）是一种利用安装在运载体上的陀螺仪和加速度计来测定运载体位置的一个系统[1]。通过陀螺仪和加速度计的测量数据，可以确定运载体在惯性参考坐标系中的运动，同时也能够计算出运载体在惯性参考坐标系中的位置。在工作过程中，INS不与外界发生任何联系，依靠载体自身设备即可完成导航工作，具有很强的工作自主性和隐蔽性，在军事上得到了一种绝对保密不受外界干扰的导航系统，因而广泛地应用于航天、航空、航海等重点国防领域。

INS可以分为平台惯导系统、捷联惯导系统。捷联惯导具有结构简单，安装维护方便，体积小、重量轻、成本低、导航信息丰富、有较强的系统综合能力等特点。

综上所述，GNSS导航和惯性导航系统（INS）都是当前主流的导航系统，但是二者都有各自优缺点，如果将GNSS和INS组合的导航系统能在发挥各自优势的同时，取长补短弥补单一系统的不足。为了开发出高精度的GNSS/INS组合导航定位系统，展开相应的关键技术研究不但具有理论意义，而且具有重要的经济价值。

1 GNSS/INS组合导航系统状态方程的分析

文章尝试采用的是位置、速度组合的模型进行GNSS/INS导航系统建模。当组合系统采用线性卡尔曼滤波器的时候，常常是利用间接法进行估计，滤波器的状态为导航参数的误差等。上文提到的系统，实际上是导航系统中各种误差的“组合体”，滤波器估计值的主要部分是导航参数误差的估计值，然后利用估计值去校正惯性导航系统INS的导航参数[4]，或者通过下文提到的构建神经网络的方法，更加准确地校正INS的导航参数。

相关文献[1,3]和数学公式表示，惯性导航系统的误差方程包括平台误差角、速度误差、位置误差以及惯性器件的误差。

GNSS/INS组合系统的状态变量，由INS误差状态的变量和GNSS误差状态的变量组成。是否需要增加和需要增加那种类型的GNSS误差状态的变量，由GNSS和INS的组合的方式，以及选择那种GNSS观测信息作为INS滤波器的量测输入信息决定。

如果采用的是分布式组合方式。对于分布式组合的方式，系统中的两个卡尔曼滤波器分别处理INS和GNSS的数据，两个滤波器的误差状态方程单独建立。

1.1 INS误差状态方程

以上讨论了惯性导航系统的主要误差方程，将平台误差角方程、速度误差方程，位置误差的方程，以及惯性仪表的误差方程，和加速度计的误差结合在一起，可以写出INS系统的误差的状态方程，一般表达式为：

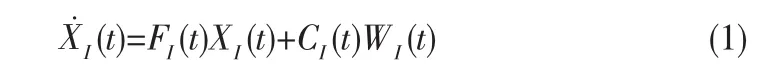
式中，FN是对应于INS的九个误差方阵。

1.2 GNSS状态方程

GNSS的状态类似于INS中的一样，选择位置的误差和速度的误差。在单独的GNSS航定位系统的实际应用中，常常是在载体的初始位置和速度已知的情况下，可以单独使用GNSS测信息。可以利用伪距的载波相位，多普勒频率以及相关的参数，来计算在接收机的数据采集周期中的位置和速度的改变数，来实现导航的定位[1]。GNSS定位的位置和速度的改变数使用状态空间的模型来描述的话，一般表达式为：

式中，XG为n维的状态向量；FG为GNSS的n×n阶动态矩阵；GG=I为单位矩阵；WG为n维的系统噪声。

2 GNSS/INS组合系统的量测方程

当GNSS/INS的组合导航系统中，组合的模式选择的是位置和速度这一组合时，系统的量测方程就有2种：一种是位置测量的差值，另一种是速度量测的差值[3]。位置量测的差值，是用INS给到的位置信息和GNSS的接收机计算得到的相应的位置的信息进行求差，结果作为量测的信息；速度量测的差值，是INS所给的速度的信息和GNSS接收机所得到的速度的信息进行求差，来作为量测的信息。

INS的位置量测的信息，可以表达为地理坐标系下真实值和对应的误差之和，GNSS的接收机所出的位置量测信息，可以表达为地理坐标系下的真值和对应的误差之间的差值。因此形成了GNSS和INS的位置和速度的组合系统的量测方程。表达式如下：

3 基于分布式卡尔曼滤波和RBF神经网络预测INS误差反馈校正的方法

顾名思义，为先根据GNSS/INS在正常工作下的输出信号作为神经网络的学习，从而确定神经网络的构建，得到最优的神经网络模型。为了达到神经网络与系统的最佳匹配性，在神经网络学习的之前，先设计通过匹配的卡尔曼滤波器进行“野点”去除，从而保证神经网络学习的参考数据是可靠的。

3.1 分布式卡尔曼滤波数据预处理

如果使用普通的卡尔曼的滤波器，则要求GNSS的输出位置、输出速度的误差均为白噪声。但事实上，GNSS的接收机的输出位置、输出速度的信息误差是与时间都相关的函数。为了解决这样的问题，以及尽可能地减少误差对系统的影响。可以采取两种方法来避免和减少不必要的误差，一个是加大集中式的卡尔曼滤波器的迭代周期，另一个是采用分布式的卡尔曼滤波器进行组合应用。相关资料表示[5]，采用加大集中式的卡尔曼滤波器的迭代周期的方法会导致组合的系统导航精度下降。

分布式滤波器设计的组合滤波器不再要求GNSS输出的位置误差和速度误差必须为白噪声。这种方案的缺点是GNSS滤波器和组合滤波器之间会有较大的数据通信量。在按照下述的方式构建组合滤波器状态估计的时候，不仅仅GNSS滤波器的滤波值要作为主滤波器的量测输入，而且GNSS滤波的预报值，也要作为主滤波器的量测输入。实际在构建分散滤波的时候，往往略去预报值，只输入滤波器的滤波值作为量测的修正。

3.2 RBF神经网络预测INS误差补偿

最基本形式的RBF网络包括3层，每一层都有完全不同的作用。输入层由一些感知单元组成，它的作用是将网络与外界的环境连接起来。第二层也就是在网络中的一个隐层，它的作用是从输入空间到隐藏空间之间进行非线性的变换，一般情况下，隐藏空间有着较高的维数存在[2]。输出层是线性的，它可以作用在输入层的激活模式并提供响应。基本结构如图1所示。

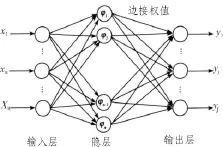
图1 RBF神经网络结构Fig.1 RBF neural network structure

RBF神经网络的建立主要是通过学习产生的，第一阶段是自组织学习阶段，也就说学习隐层基函数的中心和方差；第二阶段是监督学习，即学习输出层权值，通过先前获得的样本来进行学习[6]。

3.3 数据预处理和误差补偿算法

由于系统的本是误差的综合体，因此选取神经网络的输入为INS陀螺仪和加速度的输出，输出为相应的INS的位置误差、速度误差和姿态误差。

当GNSS信号正常时，对神经网络进行训练。GNSS信号和INS组合导航的滤波输出作为目标网络的输出，同时陀螺仪和加速度计的输出作为目标网络的输入。训练算法不断修正网络参数，从而达到误差的最小均方值。当GNSS信号中断时，INS的陀螺仪和加速度计的输出作为已经训练好的神经网络的输入，从而来预测相关的位置误差、速度误差和姿态误差，达到对当时INS误差的补偿，通过矢量加的到最终载体的位置和运动情况。如图2所示。

图2 神经网络训练和预测过程Fig.2 Training and forecasting process of neutral network

4 跑车和仿真实验

为了验证算法的有效性和健壮性，采用了实验室自助研制的组合导航硬件系统进行了跑车实验和数据仿真工作：车辆的平均车速为50 km/h,跑车线路为上海紫竹科技园区。为了比较预测的准确性，人为制造GNSS“失锁“，并在失锁前，开始GNSS/INS的训练，在失锁后，切换为预测模式。然后将预测的数据和GNSS失锁时的数据进行对比。

参考图3，从图中可以认为，卡尔曼滤波和RBF神经网络预测的结果比单RBF神经网络预测来得准确。从经纬度上来说，卡尔曼滤波加RBF神经网络预测的误差大约在3 m左右，可以认为是可靠结果，因此可以认为当GNSS失锁情况下，利用INS的辅助下，系统仍可靠，保持时间大约在30 s左右。

5 结束语

文中提出的是利用分布式卡尔曼滤波和神经网络结合来进行在GNSS失锁的情况下，通过INS的误差补偿，进行对载体运动姿态和航向的预测。在通过大量实验和算法验证后，得到的实验结果比较良好。这样的实验结果预示着通过对大数据的分析和评估，可以预测出未来会发生的运动状态和姿态的改变等。GNSS/INS组合导航系统一直在导航领域有着广泛而深刻的影响。在后续的工作中，如果出现长时间的GNSS失锁，那么神经网络和卡尔曼滤波的模型还需要进一步研究，如何改进神经网络的学习快速和准确性，应该是下一步研究的重点。

图3 左图为失锁情况下神经网络预测的纬度，右图为失锁情况下神经网络预测的经度Fig.3 Left is the latitude forecast and right is longitude forecast

[1]Grewal M S,Weill L R,Andrews A P.Global positioning systems,inertial navigation and integration[M].New York: Wiley Inter-science,2007.

[2]Sharaf R,Noureldin A.Online INS/GPS integration with a radial basis function neural network[J].IEEE Aerospace and Electronic Systems Magazine,2005(20):8-14.

[3]Yu M J,Park H W,Jeon C B.Equivalent nonlinear error models of strapdown inertial navigation systems[R].AIAA-97-3563,1997:581-587.

[4]曹娟娟，房建成，盛蔚，大失准角下MIMU空中快速对准技术[J].航空学报，2007,28(6)：1395-1400.CAO Juan-juan,Fang Jian-cheng,SHENG Wei.A fast inflight alignment for MIMU under large attitude errors[J].Chinese Journal of Aeronautics,2007,28(6):1395-1400.

[5]Julier S J,Uhlmann J K.Unscented filtering and nonlinear estimation[J].Proceedings of the IEEE,2004,92(3):401-422.

[6]高隽，人工神经网络原理及仿真实例[M].北京：机械工业出版社，2003.

The study of error correction based on Kalman filter and neural network in the GNSS/INS system

ZHANG Jing-xian,YANG Ying-dong,QIAN Feng
（Navigation and Control Institute,School of Electronic Information and Electrical Engineering,Shanghai Jiaotong University, Shanghai 200240,China）

When GNSS signal cannot be received,the error of GNSS/INS integrated navigation system will be accumulated with time and system will lose the navigation function.Through theoretical analysis and mathematical modeling,this paper presents a method based on Kalman filter and RBF neural network in order to make up the loss of GNSS defects.Kalman filter preprocess the data before RBF neural network training.After experimenting and simulating,we confirmed the feasibility of the method is strong.The average positioning error is about 3 meters,and can predicate the location for about 30 seconds.

Kalman filter;neural network;GNSS;strapdown inertial navigation system

TP391.9

A

1674－6236（2015）10-0103-03

2014-08-26 稿件编号：201408154

张静娴(1989—)，女，上海人，硕士研究生。研究方向：导航与制导，控制工程。