基于微粒群算法的BBMC控制参数优化研究
2015-12-15黄毅张小平吴亮红文天旭
黄毅,张小平,吴亮红,文天旭
(1.湖南科技大学 先进矿山装备教育部工程研究中心,湖南 湘潭 411201;2四川海洋特种技术研究所,四川 成都 610041)
0 引言
矩阵变换器(Matrix Converter,MC)是一种具有简单拓扑结构和一系列理想电气特性的新型电力变换器[1-2],然而由于存在电压传输比低等缺陷而限制了其推广应用[3]。据研究,通过改变控制策略可有效提高电压传输比[4-5],但效果不理想,如输出谐波过大。为此,文献[6]从改变矩阵变换器主电路拓扑结构出发进行研究,提出了一种称为BUCK-Boost矩阵变换器(BUCK-Boost Matrix Converter,BBMC)的主电路拓扑结构,该结构有效解决了传统矩阵变换器电压传输比低的问题。而针对该拓扑结构,文[7]提出采用双闭环控制策略进行控制,取得了较好的控制效果。然而在该控制策略中的相关控制参数却因采用试凑法获得而难以达到最佳控制效果。为此,本文提出采用微粒群算法(Particle Swarm Optimization,PSO)对其控制参数进行优化。文中阐述了微粒群算法的基本原理,重点研究了采用该算法对双闭环控制策略中的控制参数进行优化的具体设计方法,并采用MATLAB对其控制效果进行了仿真验证,同时与采用试凑法获得的控制参数进行了对比仿真分析。
1 BBMC拓扑结构及基本原理
三相-三相BBMC拓扑结构如图1所示[6]。该结构采用AC-DC-AC双级变换器的结构形式,中间直流环节无储能元件;其整流级为一个3/2相矩阵变换器,逆变级则为三相BUCK-Boost逆变器的结构形式,其特点为通过调节占空比可实现对其输出电压的任意调节。

图1 三相-三相BBMC拓扑结构
2 BBMC双闭环控制策略简介
针对BBMC的逆变级采用双闭环控制策略进行控制[7],取得了较好的控制效果。该控制策略由电感电流控制内环和电容电压控制外环组成。
电感电流控制内环如图2所示。该控制环以电感电流的参考值iL1ref与其实际值iL1进行比较,其偏差经PI运算得电感电压的参考值uL1ref,同时通过检测电容电压uc1和直流侧电压,由公式(1)即可计算得到占空比d1,将其限幅后控制BUCK-Boost变换器中功率开关的开关时间,由此来调节电感电流iL1使其按参考值iL1ref变化。

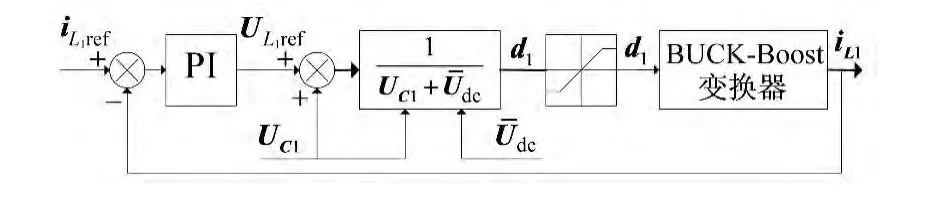
图2 电感电流控制内环原理图
电容电压控制外环如图3所示。该控制环以电容电压的参考值uC1ref与其实际值uC1进行比较,其偏差经PI运算得电容电流的参考值uC1,同时通过检测输出电流i1、电容电压ic1和直流侧电压,由公式(2)即可计算得到内环电感电流的参考值iL1ref。将其限幅后作为控制内环的参考输入,并通过控制内环改变占空比d1来调节电容电压uc1,使其按设定的参考值uc1ref变化,由此可在输出侧获得所需的输出电压。
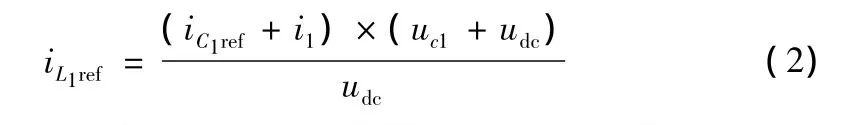

图3 电容电压控制外环原理图
3 采用微粒群算法优化双闭环控制的控制参数
鉴于BBMC输出波形的谐波失真度与双闭环控制策略中的PI控制参数直接相关,而文献[7]中该控制参数为采用试凑法获得,因而难以达到最佳控制效果,为此采用微粒群算法对该控制参数进行优化。
双闭环控制中PI控制参数优化可以看成是一个多目标的优化问题,一般试凑法很难同时兼顾多个目标同时进行优化,因而难以获得最佳的PI控制参数,而微粒群算法具有良好的全局搜索和多目标优化能力,是一种成熟有效的优化算法,能有效克服试凑法的局限性,适用于对该控制参数进行寻优[8-9]。
3.1 微粒群算法基本原理
微粒群算法的基本思想是通过群体中个体之间的协作和群体信息共享来寻找最优解。假设在D维的寻优空间中,有M个粒子组成的种群,每个粒子的当前位置由位置矢量Xi=(xi1;xi2;…;xiD),i=1,2,…,M来表示,每个粒子的移动速度由速度矢量Vi=(vi1;vi2;…;viD),i=1,2,…,M 来表示,每个粒子都有一个目标函数确定的适应值,由适应值可得出每个粒子经历过的历史最好位置,即个体极值,记为 Pi=(pi1;pi2;…;piD),i=1,2,…,M,这可看成粒子的自我经验。另外,通过适应值也可获得种群经历过的历史最好位置,即群体极值,记为Pg=(pg1;pg2;…;pgD),这可看成是粒子的群体经验。粒子通过自我经验和群体经验可决定下一步的运动。在粒子运动过程中,第i个粒子从第k步到第k+1步的移动,可由下面的速度和位值更新公式得到:

其中 i=1,2,…,M,d=1,2,…,D,W 是惯性权重因子,c1和c2是加速因子,rand()是[0,1]范围内的随机函数。惯性权重因子w在整个寻优过程中并非一直不变,而是随着迭代次数线性减少。

其中k=1,2,…,kmax,wk是第k次迭代用的惯性权重因子,wmax和wmin分别是惯性权重因子的最大值和最小值。惯性权重因子线性减少有利于寻优初期以比较大的惯性权重因子加速扩展搜索空间,而在后期以比较小的惯性权重因子加强局部精细搜索的能力。
3.2 采用PSO优化PI控制参数
通过优化PI控制参数,使基于双闭环控制策略的BBMC输出波形的谐波失真度达到最小。因此取BBMC输出的谐波失真度(THD)作为微粒群算法的适应值,适应值公式如下:
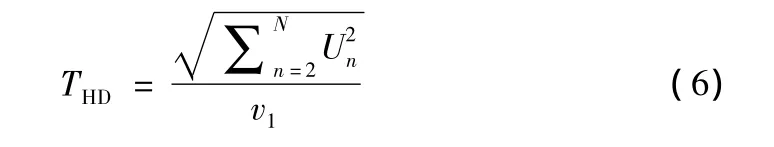
其中Un为n次谐波电压有效值;N为所能考虑的最高谐波次数;U1为基波相电压有效值。设种群规模为M,每个种群粒子的位置矢量Xi由电容电压控制环中PI控制器的比例系数kp1、积分系数ki1和电感电流控制环中PI控制器的比例系数kp2、积分系数ki2组成,即粒子矢量维度D=4,其搜索范围以试凑法得到的控制参数为核心,向周围扩散形成,如果优化结果接近搜索空间的边缘,则可以在该优化结果的基础上进一步扩展。采用微粒群算法优化PI控制参数结构框图如图4所示。

图4 PSO优化PI控制参数结构框图
采用微粒群算法优化PI控制参数的流程如图5所示。
第一步;初始化:确定种群规模M、粒子矢量维度D、最大迭代次数kmax、随机初始化粒子位置和速度。
第二步;计算适应值:将各个粒子矢量导入基于双闭环控制的BBMC模型中,获得该粒子的适应值,即BBMC输出的谐波失真度,并计算其个体极值和群体极值。
第三步;更新极值:将该粒子的当前适应值与该粒子个体极值的适应值进行比较,如果该粒子的当前适应值小于该粒子个体极值的适应值,则该粒子的当前位置成为该粒子新的个体极值;将该粒子的当前适应值与群体极值的适应值比较,如果该粒子的当前适应值小于群体极值的适应值,则该粒子的当前位置成为新的群体极值。
第四步;更新粒子位置和速度:根据公式(3)~(5)更新粒子速度、位置和惯性权重因子,若粒子速度大于vmax,则该粒子的速度限定为vmax,若粒子位置超出搜索空间,则将该粒子位置限定在搜索空间的边缘位置。
第五步;判断迭代次数:判断迭代次数是否达到最大值,如果达到最大值,输出优化结果,否则返回第二步继续寻优。
4 仿真分析

图5 PSO优化PI控制参数流程图
利用MATLAB对采用微粒群算法优化获得的控制参数的控制效果进行仿真验证。假设三相电源,功率开关,电感及电容等均为理想元件。仿真参数设置如下:
输入为220 V/50 Hz对称三相交流电源;电感与电容分别取:Li=1.3×10-4H,Ci=5.4×10-5F,i=1~3;采用三相对称阻感负载,其电阻和电感分别为:Ri=50 Ω,Lj=300 μH,j=1 ~3;粒子矢量维度D=4,种群规模M=30,最大迭代次数kmax=50,惯性权重因子最大值wmax=0.9,最小值wmin=0.4,加速因子c1和c2取2.0,电容电压控制环PI调节器中kp1的搜索范围为[0,10],ki1的搜索范围为[0,1],电感电流控制环中PI调节器kp2的搜索范围为[0,1 000],ki2的搜索范围为[0,1]。为验证微粒群算法的优化效果,任取不同参考电压150 V/25 Hz、311 V/50 Hz及450 V/75 Hz与试凑法获得的控制参数进行对比仿真分析。
试凑法获得控制参数为 kp1=5.538、ki1=4.99 ×10-4、kp2=80及ki2=8.44×10-5,在满足不同参考电压条件下,PSO优化得的控制参数见表1。
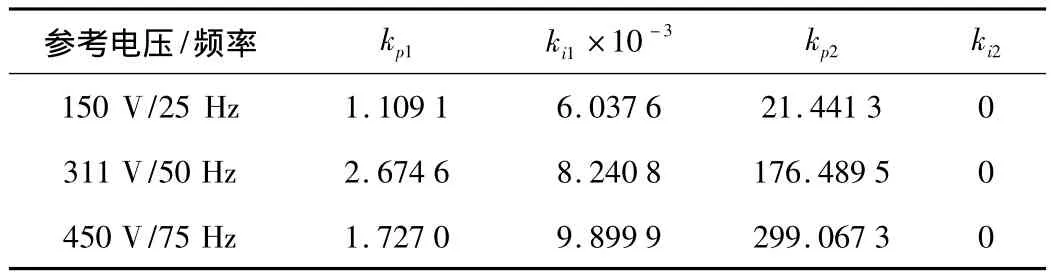
表1 PSO优化控制参数结果
其仿真波形分别如图6~8所示,仿真结果见表2。

表2 仿真结果

图6 参考电压为150 V/25 Hz的仿真波形

图7 参考电压为311 V/50 Hz的仿真波形

图8 参考电压为450 V/75 Hz的仿真波形
由仿真波形及表2可见:采用微粒群算法优化获得的PI控制参数较试凑法获得的PI控制参数具有更好的控制精度,其输出波形的谐波失真度更小。
5 结束语
针对采用试凑法获得BBMC双闭环控制策略的PI控制参数难以获得最佳控制效果的状况,提出采用微粒群算法对该控制参数进行优化,介绍了微粒群算法的基本原理,阐述了采用该算法优化PI控制参数的设计方法,并对优化获得的PI控制参数进行仿真验证,同时与采用试凑法获得的PI控制进行了对比仿真分析。结果表明:采用微粒群算法优化获得的PI控制参数较试凑法获得的PI控制参数具有更好的控制精度,其输出波形的谐波失真度更小。
[1]XING W W,HUA L,HONG W S,et al.A research onspace vector modulation strategy for matrix converter under abnormal input-voltage conditions[J].IEEE Transactions on Industrial Electronics,2012,59(1):93-104.
[2]YAMAMOTO E,HARA H,UCHINO T,et al.Development of MCs and its applications in industry[J].IEEE Transactions on Industrial Electronics,2011,5(1):4-12.
[3]ATIFL,AHMED S K,HAITHAM A.Space vector PWM technique for a three-to-five-phase matrix converter[J].IEEE Transactions on Industry Applications,2012,48(2):697-707.
[4]朱建林,张建华,郭有贵,等.过调制矩阵变换器的电压传输特性及谐波分析[J].中国电机工程学报,2007,27(10):110-113.
[5]CHANG J,SUN T,WANG A H.Highly Compact AC-AC Converter Achieving a High Voltage Transfer Ratio[J].IEEE Transactions on Industrial Electronics,2002,49(2):345-352.
[6]张小平,朱建林,唐华平,等.一种新型BUCK-Boost矩阵变换器[J].信息与控制,2008,37(1):40-45.
[7]张小平,朱建林,唐华平,等.新型Buck-Boost矩阵变换器的双闭环控制策略[J].控制理论与应用,2009,26(2):203-208.
[8]GONG Y J,ZHANG J,LIU O,et al.Optimizingthe vehicle routing problem with time windows:a discrete Particle Swarm Optimization approach[J].IEEE Transactions on Systems,2012,2(42):254-267.
[9]WU C W,MEN S T.Application of Enhanced Integer Coded Particle Swarm Optimization for Distribution System Feeder Reconfiguration [J].IEEE Transactions on Power Systems,2011,26(3):1591-1599.
