基于模糊策略的PID控制器在恒温控制中的应用
2015-12-15郑向军徐锋应一镇杨彦青
郑向军,徐锋,应一镇,杨彦青
(台州职业技术学院自动化研究所,浙江 台州 318000)
0 引言
PID控制由于算法简单、稳定性好、可靠性高等优点,广泛应用于温控系统。实际应用中,PID参数主要凭经验选定,且一旦选定不再更改。由于温控系统的大惯性、时变性的特点,加之控制过程中某些参数会随时间发生变化[1],这种定值PID控制往往无法取得满意的结果。
模糊控制不依赖被控对象的精确模型,控制规则基于操作者的经验,具有较强的鲁棒性和容错性[2]58,能有效地减小干扰和参数变化对控制效果的影响,适合非线性、时变及滞后系统的控制。
将模糊控制策略应用于PID参数的在线整定,根据实时状态对PID参数进行在线优化,可以提升温控系统的品质。通过仿真和对RX3-4的实验测试,表明这种控制方法较传统的PID控制更具优势。
1 控制系统原理与结构
1.1 温控系统的特性
传统的PID控制器参数的确定主要取决数学模型。温度控制系统是一个具有蓄势能力的装置,其数学模型均可表示为以下形式:
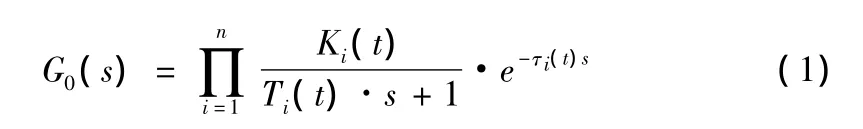
式中G0为传递函数;n为系统的阶次;Ki(t)为时变比例系数;τi(t)为时变滞后时间常数,Ti(t)为时变时间常数[2]87。
温控系统具有非线性、大惯性、大滞后和时变性特点,且受外界干扰因素较多,参数变化无常。(1)式中的 Ki(t)、Ti(t)和τi(t)很难用数学函数精确表达[2]67。其模型具有不确定性且无规律可循。
由于上述特点,采用传统的定值PID控制时,在参数KP、KI、KD的选择上存在较大的困难,参数无法始终适应系统的时变性要求,从而影响控制效果。
1.2 系统原理与结构
结合模糊控制和PID控制的优点,构成Fuzzy-PID控制器,模糊控制器根据不同的输入情况和控制要求,实时修订PID控制器的参数,实现KP、KI、KD参数的在线优化。图1为RX3-4-8恒温炉控制系统的结构简图。
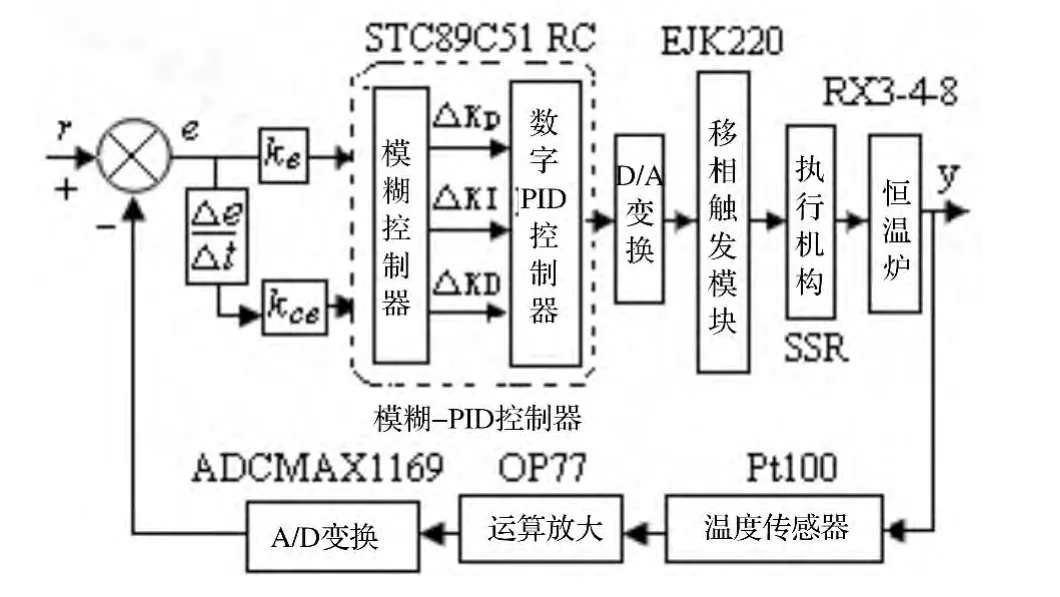
图1 RX3-4-8恒温炉控制系统结构简图。
控制系统以STC89C51单片机为控制器核心,STC89C51具有温度采集、串行通信、A/D和D/A转换、模拟量输出等多种功能,其CPU具有超强的抗干扰能力,能较好地满足控制要求[3]21。采用检测精度高、稳定性高、防水性好、测温范围宽的高精度铂热PT1000电阻为温度传感器。为减小非线性误差,温度采集电路采用恒流源式[4]。
系统将采集到的温度信号经运算放大和A/D转换等处理,送入单片机进行Fuzzy-PID运算以及D/A转换后输出控制量,再由移相触发模块EJK220和随机型电压调节模块SSR实现电压的调节[3]22。
2 控制系统设计
2.1 数字PID算法设计
STC89C51单片机构成的数字PID控制器由于具有编程灵活性和强大的数据处理、存储功能,因此能方便地设计出灵活多样和满足控制要求的多种PID算法[5]9。标准的数字PID算法如下式所示:
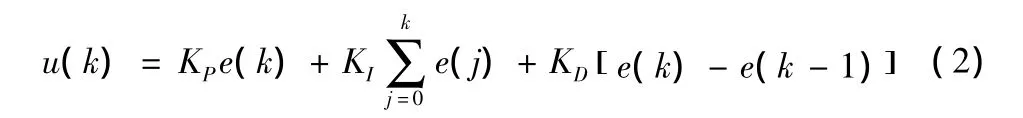
上式的Kp为确比例系数,KI为积分系数,KD为微分系数,u(k)为kT采样时刻的输出。
由于(2)式的积分项∑e(j)保留了所有kT时刻之前的偏差值,易造成累计误差,又占用很多内在空间,使用起来不方便。因此本系统采用增量型PID控制算法[5]10,即PID控制器的输出只是控制量的增量Δu(k):
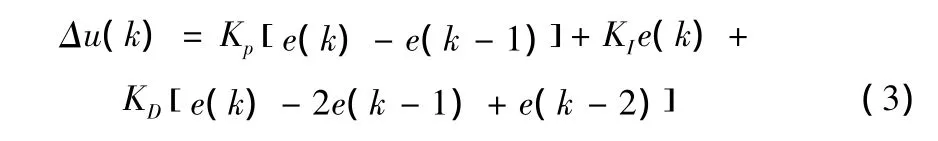
增量型PID控制算法在k采样时刻的实际输出量为:
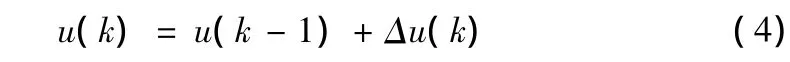
在采样周期T不变情况下,当KP、TI、TD参数确定后,只要使用前后三次测量的偏差值即可由(3)式或(4)式计算出控制量。
2.2 模糊控制器设计
Fuzzy-PID控制系统设计的核心工作是模糊控制器的设计,包括输入/输出语言变量的确定,量化因子和比例因子的确定、隶属度函数的选取、模糊规则制订、选择模糊推理和反模糊化方法等。
2.2.1 模糊控制器结构
本例的模糊控制器采用二维结构,目标函数为恒温炉的温度,输入为偏差e(被调量与设定值差)和偏差变化率△e/△t,输出量为 PID 控制器参数修正值△KP、△KI、△KD[6]。
模糊控制器结构如图2所示。
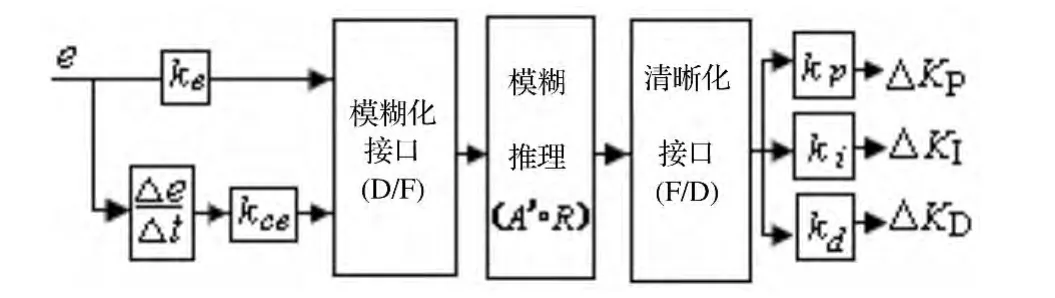
图2 模糊控制器结构示意图
图 2 中,ke和 kce为模糊控制器量化因子,kp、ki、kd分别为模糊控制器输出的比例因子。
2.2.2 模糊化处理
模糊控制器输入偏差和偏差变化率的语言变量分别选为E、EC,输出语言变量分别选为ΔKp、ΔKi、ΔKd。将输入和输出语言变量均分割为7个模糊子集,并用正大(PB)、正中(PM)、正小(PS)、零(ZO)、负小(NS)、负中(NM)、负大(NB)描述[7],即:
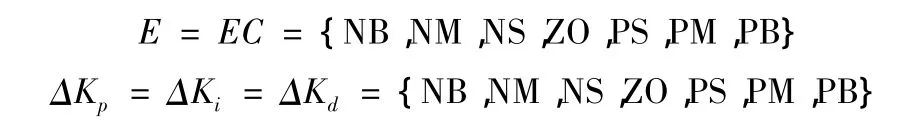
本例中温度偏差的基本论域定为[-1,+1],为提高控制系统的灵敏度,实际应用时将温度偏差的基本论域提高20倍,即偏差基本论域即扩大到[-20,+20],选定偏差语言变量E的论域为{-6,-5,-4,… -0,+0,… +5,+6}共14 个等级,偏差变化率语言变量EC的论域为{-6,-5,-4,…0,… +5,+6}共13个等级,输出语言变量的论域为{-7,-6,-5,…0,… +5,+6,+7}共15个等级。
根据温控制系统的特点和控制要求,并考虑到计算的方便,本例中输入输出变量隶属函数采用图3所示常见的三角形,由此可以计算出语言变量各档的隶属度值。
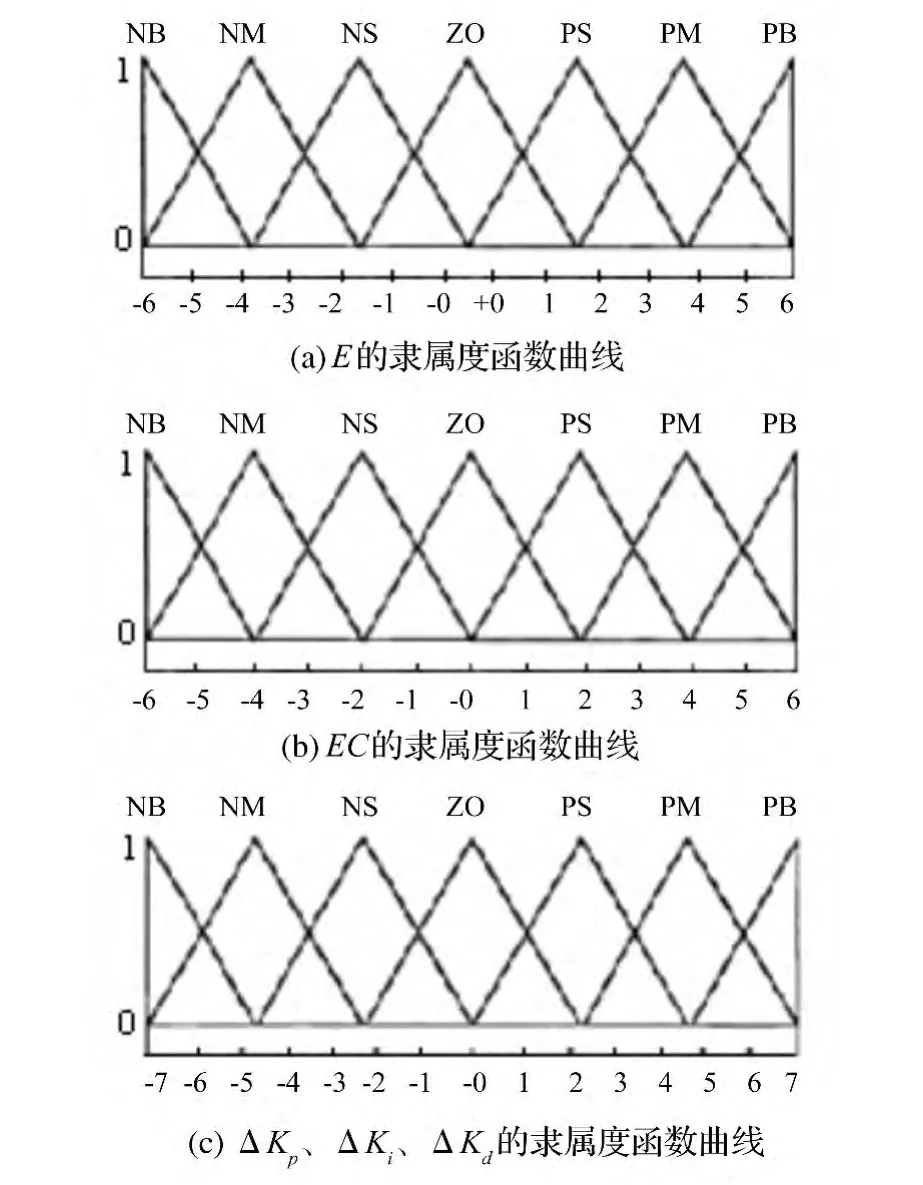
图3 输入/输出变量的隶属度函数曲线
2.2.3 模糊规则
理论分析可知,PID控制器的KP、KI、KD参数与偏差e和偏差变化率Δe/Δt之间存在一种非线性关系,这种关系虽然无法用清晰的数学语言描述,却可以用模糊语言描述。
图4为典型温控系统PID控制输出响应曲线和偏差e、偏差变化率 de/dt曲线[8]。
根据图4曲线可以总结出了输出y和输入e、de/dt之间的对应关系,可归纳总结出PID参数与偏差e和偏差变化率de/dt之间的模糊关系。
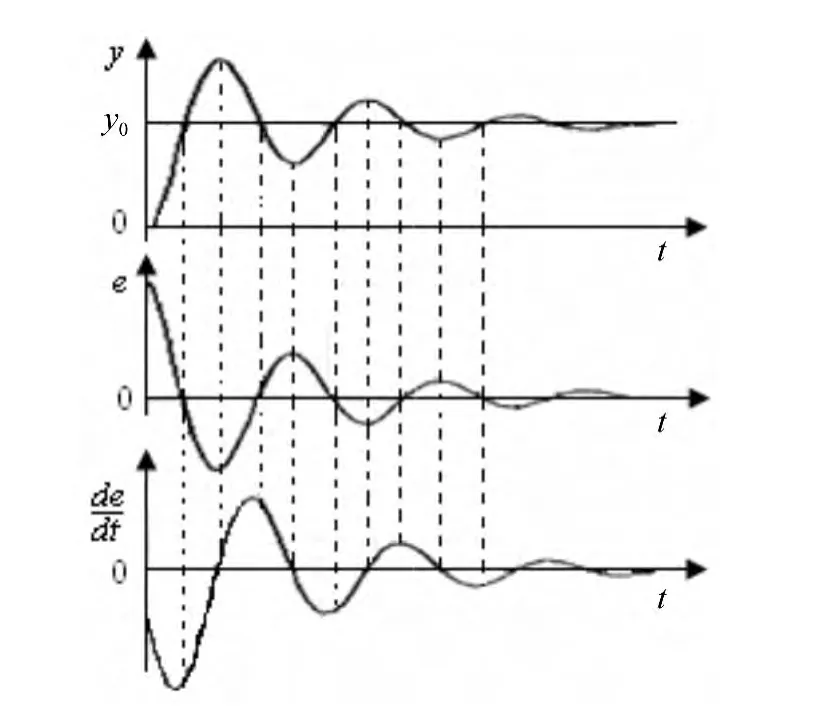
图4 典型PID曲线与e,de/dt之间的关系
(1)当|e|较大时,为了加速响应过程,应取较大的KP值,这样可以使系统的时间常数和阻尼系数减小;为了避免系统开始时可能引起的超范围控制作用,取较小的KD值以便加快系统的响应速度;为了避免出现较大的超调,可去掉积分作用,即 KI取零[9]。
(2)当|e|和|de/dt|中等大小时,取较小的KP值,以便使系统的超调降低;为保证系统的响应速度,KD和KI值要恰当。
(3)当|e|较小时,为了使系统有良好的稳定性,取较大的KP和KI值。当|de/dt|较小时,KD值可取中等大小,当|de/dt|较大时,KD值可取较小。
基于以上总结出的输入变量 e、de/dt与参数 KP、KI、KD之间的关系,结合工程技术人员的实际操作经验并通过实验调整,最终得出模糊推理规则。
表1为本例的模糊推理规则表。
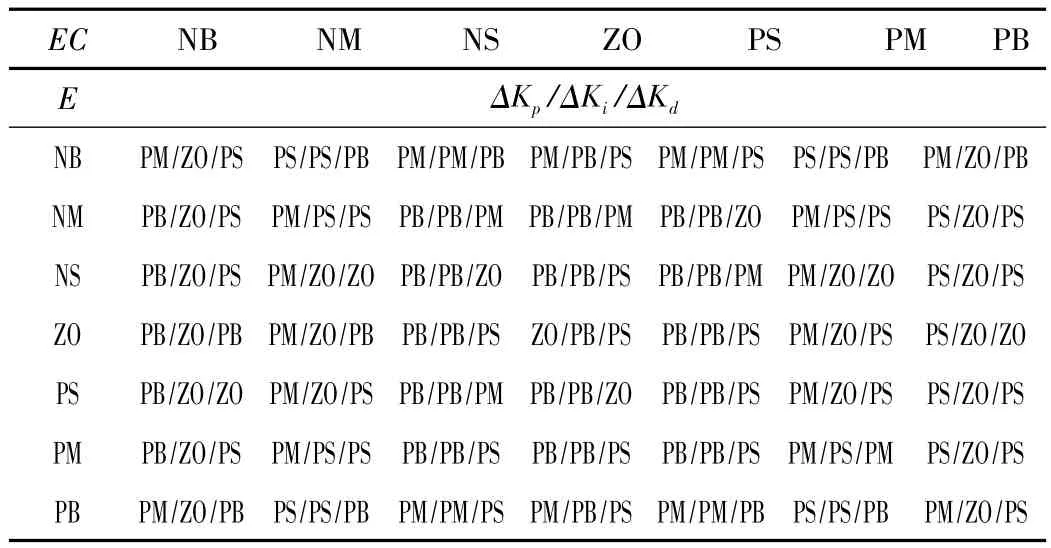
表1 模糊推理规则
2.2.4 模糊推理
模糊推理是一种近似推理,目前常用的方法主要有Zadeh(扎德)、Mamdani(马丹尼)和 Tsukamoto(楚卡莫托)法等多种。本例的合成推理采用Mamdani法。
模糊控制器规则库中的规则分三组,每组49条控制规则,对于单变量二维结构的模糊控制器,常采用if Aiand Bithe Ci形式[7],具体到各组的每条模糊规则的表述如下:
(1)if E is NB and EC is PB the ΔKpis PM,ΔKiis ZO,ΔKdis PS;
……………………
(49)if E is PB and EC is NB the ΔKpis PM,ΔKiis ZO,ΔKdis PS;
……………………
上述if Aiand Bithe Ci形式的模糊条件语句的模糊蕴涵关系Ri,根据 Mamdani法,当 Ai∈U,Bi∈V,Ci∈W 时,其三元模糊关系为:
Ri=Ai× Bi× Ci,或 Ri(u,v,w)=Ai(u)∧Bi(v)∧Ci(w)把上述每条规则的蕴涵关系Ri作并运算即可得到系统各组总的模糊蕴涵关系R:
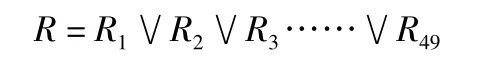
当控制器采样得到的变量经量化和模糊化处理映射成模糊E和EC后,按近似推理合成法则得到输出模糊量。例如,系统当前状态是Ei和ECj,则模糊控制器的输出△Kij为:
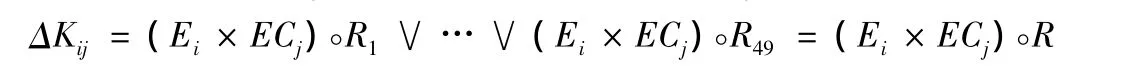
2.2.5 清晰化处理
经过模糊推理后,输出的是一个模糊集合,是由一个有多条模糊控制规则所得出的综合,因此需要将其等效为一个清晰值,即映射到输出基本论域中某个精确的值上。本例采用加权平均法,其控制量的精确值可由输出的隶属度函数加权平均判决得到[10],即:
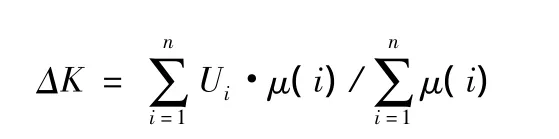
式中△K为模糊控制器输出的修正值(△KP、△KI、△KD)。Ui是输出模糊集合中第i条规则隶属度函数的中心值;μ(i)是输出模糊集合的隶属度。
数字PID控制器比例-积分-微分系数的精确值的计算公式如下:
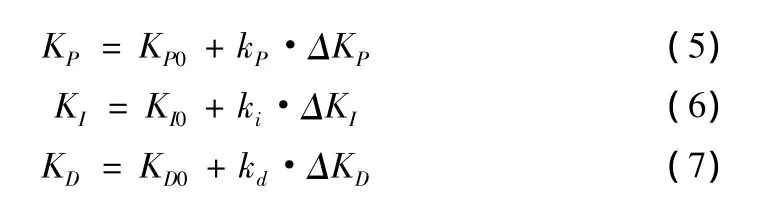
(5)~(7)式中,ΔKP、ΔKI、ΔKD是模糊控制器的输出;KP0、KI0、KD0是PID参数的初始值。
3 系统仿真与实验
3.1 模糊-PID控制器仿真
控制系统仿真采用MATLAB/Simulink工具软件,构建如图5所示的仿真模型[11]。
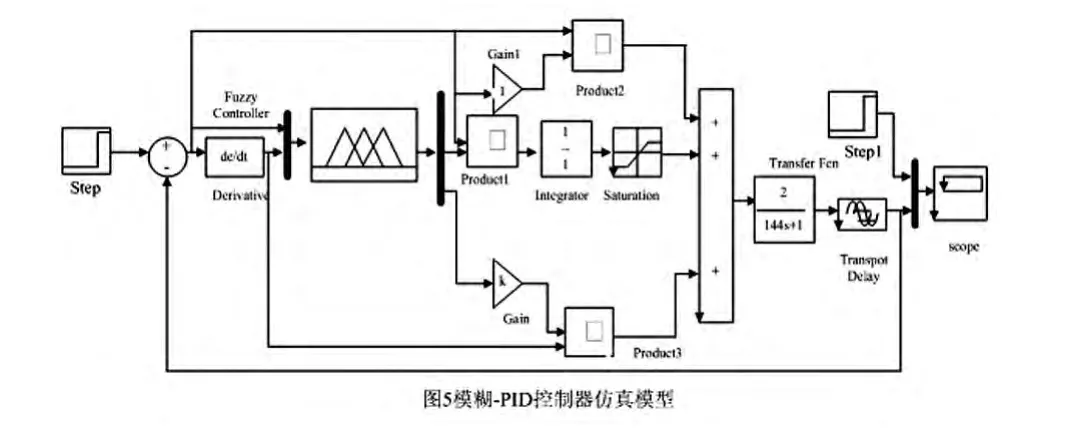
图5 模糊-PID控制器仿真模型
当给定温度t=500℃时,温度控制系统的响应曲线如图6(a)所示,可以看出,采用Fuzzy-PID控制时,系统的调节时间约90秒左右,超调量小于0.3%,稳态误差为零。
6(b)中还给出了常规PID控制器的温度仿真曲线。其中KP=2.88,Kd=42.8 和 Ki=0.05 由 Ziegler-Nichols法整定得到;可见调节时间接近300秒,且超调量很大,稳态误差为零。
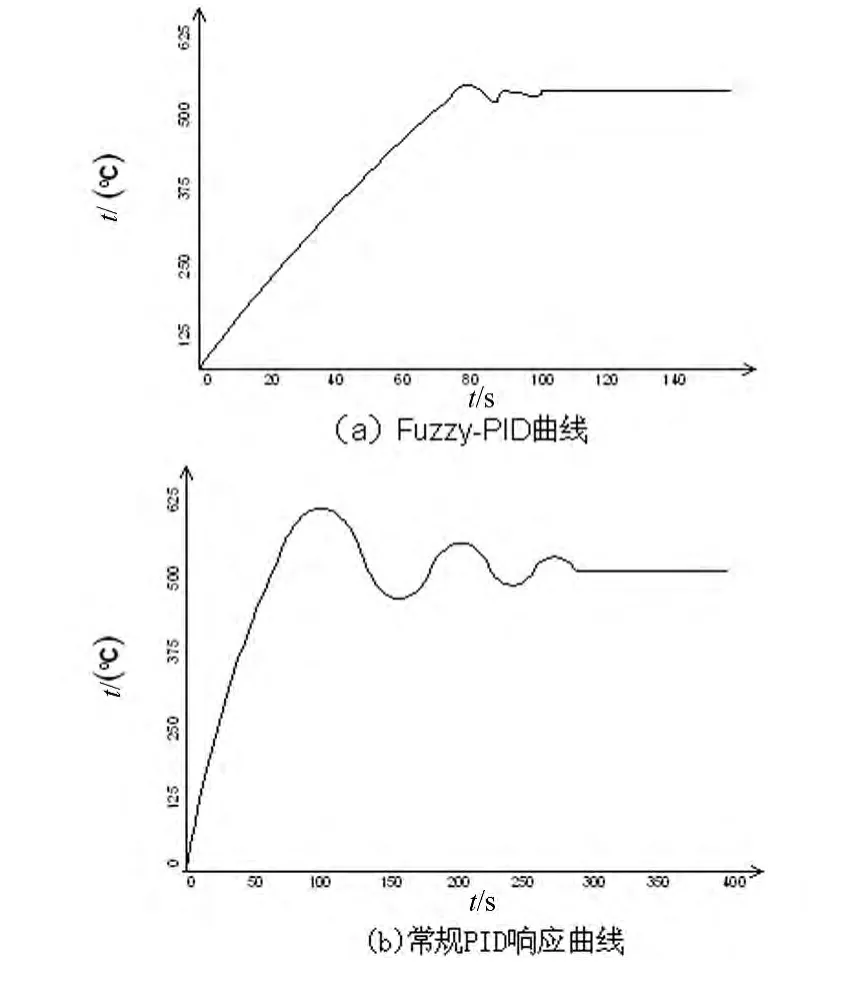
图6 温度控制系统仿真曲线
可以看出Fuzzy-PID控制系统的动态指标要优于常规PID控制器。
3.2 模糊-PID控制器实验
为了验证模糊-PID控制器的控制效果,在实验室环境下对RX3-4-8恒温炉进行多次恒温控制空载重复实验。该恒温炉的容积为260 mm×260 mm×105 mm,采用直接加热方式,加热器件功率4.0 kW。恒温炉的主要技术指标是温度在30℃ ~600℃之间可调,要求稳态误差范围不大于 ±2℃,超调量不大于0.5%。实验的间隔为2小时。
RX3-4-8恒温炉调压电路如图7所示。
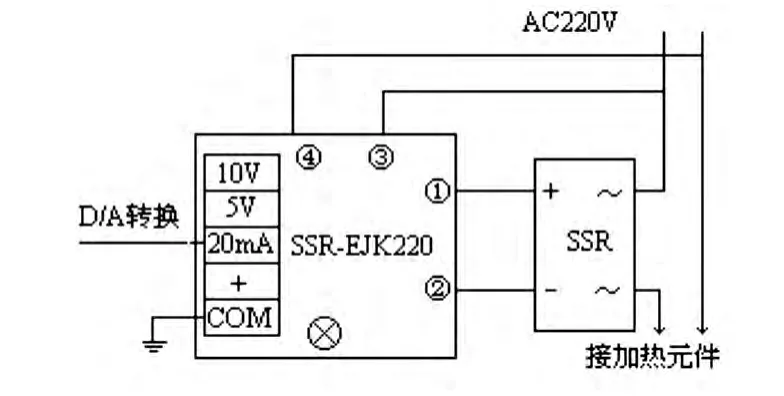
图7 箱式干燥机驱动电路
控制器运算后输出的数字信号经D/A转换为相应的模拟信号施加到移相触发模块(EJK220),再由随机型电压调节器SSR实现发热元件电压调节。
实验时,电源的额定电压为AC220 V,频率f=50 Hz,设定温度为500℃,实验测量得到三次的数据如表2所示。
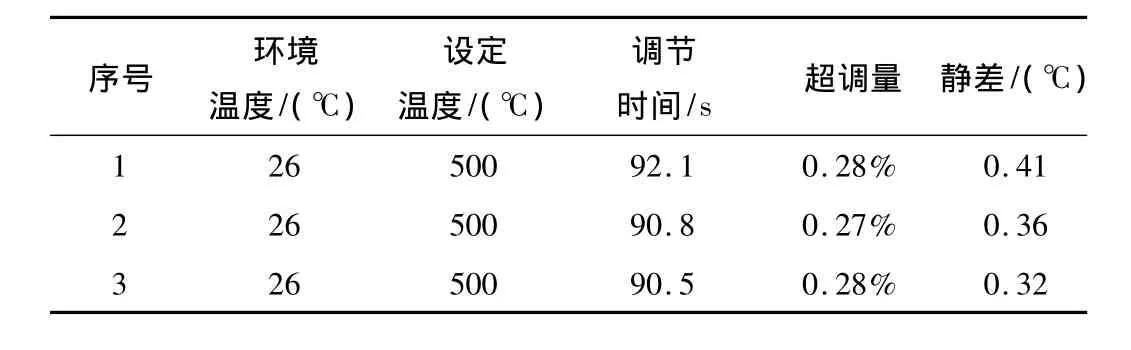
表2 重复实验数据记录
可以看出,实际调节时间均小于100 s,最后稳定误差均在1℃以内,实验与仿真的结果说明,模糊PID控制效果比较理想。
4 结束语
提出的方法克服了常规定值PID控制器参数难以适应系统参数变化的缺点[12],实现了PID参数的最优匹配。该方法能较好适应模型不确定、非线性、大滞后的时变系统。通过仿真比对和实验表明,各项指标均优于给定的技术要求,效果明显优于PID控制。该系统的成功应用,为同类温控制系统的研制提供了经验和设计参考。
[1]徐锋,郑向军,杨彦青,等.Fuzzy-PID多模控制在金属热处理恒温炉中的应用[J].电气自动化,2014,36(3):13-16.
[2]曾光奇,胡均安,王东,等.模糊控制控制理论与工程应用[M].武汉:华中科技大学出版社,2006.
[3]徐锋.一种基于PT1000的高精度电加热控制装置设计[J].电气应用,2013,32(8):20-24.
[4]郝桂青,李健飞.铂电阻温度传感器实现线性测量方案的研究[J].自动化仪表,2011,55(11):84-86.
[5]徐锋,张嫣华.数字控制系统的PID算法研究[J].机床电器,2008,35(6):8-10.
[6]牛丹,周杏鹏,陶连斌,等.模糊PID碳化硅微分恒压供水系统[J]自动化仪表,2009,53(10):26-29.
[7]徐锋.一种基于模糊控制的光伏发电系统的MPPT控制[J].电源技术,2014,38(1):92-96.
[8]郭官周,汤霞清,郭英,等.基于模糊控制器的炉温控制算法仿真与应用[J].自动化仪表,2011,55(5):42-45.
[9]李先锋.基于模糊PID的电阻炉温度控制系统研究[D].宁夏:宁夏大学,2010.
[10]石辛民,郝整清.模糊控制及其MATLAB仿真[M].北京:清华大学出版社,2008.
[11]刘金琨.先进PID控制MATLAB仿真[M].北京:电子工业出版社,2007.
[12]徐锋.基于模糊控制和功率预测的变步长扰动观察法在光伏发电系统MPPT控制中的应用[J].计算机测量与控制,2014,22(2):414-416,430.
