基于k-核解析的地震活动网络特征分析
2015-12-14李光光裴繁东
李光光 赵 海 何 璇 蔡 巍 张 娅 裴繁东
(中国沈阳110819东北大学信息科学与工程学院)
引言
地震活动以其罕见的破坏性和复杂的形成机制,成为科研工作者的重点研究对象.地质构造、介质、断裂带、时间和环境等多种因素的影响,使得人们难以准确地掌握地震形成机制,其根本原因在于地震系统具有复杂性(Taborda,Bielak,2001;Bottiglieri et al,2010).由于目前人类无法认识到地球内部的确切构造,所以仅仅从某一地区的地质构造上研究地震的发生机理收效甚微.近年来,不少研究人员开始从地震活动所形成的拓扑结构上研究地震的发生规律,并取得了一定的进展(谢周敏,2011),这为研究地震的发生规律提供了一种新的思路和方向.
复杂网络系统(周涛等,2005)是认识系统复杂性的关键,它可以从整体的角度研究复杂系统的结构和功能,探究系统内在的联系.复杂网络目前已经应用到了生物、交通和人际关系等领域,k-核则是分析复杂网络拓扑结构特性的有效工具.传统分析地震形成机制的方法会受到地理范围等因素的约束,无法将地震活动作为一个整体进行分析,而地震活动又是一种复杂的网络动力学行为(谢周敏,2011),所以从复杂网络的角度研究地震系统是很有必要的.
从复杂网络的角度研究地震的发生规律首先是由Abe和Suzuki(2004)提出的,之后一些研究人员在此基础上进行了深入研究并取得了丰硕的成果(Baiesi,Paczuski,2005;Ferreira et al,2014).他们构造地震网络的方法都是忽略地震发生时的地质构造、断裂带、介质等具体地质特征,仅将地震发生的时间、地点、震级抽象为节点,用边表示节点之间的联系,构造这样一个只有节点和边组成的网络.用这种方法构造的地震网络可以将整个地区的地震看作一个整体,着重分析地震之间的相互联系,通过对大量的地震数据进行统计分析,发现隐藏在地震数据背后的规律.
本文首先介绍基于时空影响域构造地震网络的原理和方法,然后介绍k-核的定义及其在地震网络中的应用,最后运用美国加州的地震数据详细分析最高核节点的特性,即最高核节点彼此聚集在一起,最高核所在的地理位置在接下来的时间里倾向于发生大地震,而且在一些大地震发生前,地震网络的最高核数会迅速增加,在大地震发生时最高核数达到最大值,之后又恢复到稳定状态.
1 地震网络的构造方法
地震网络主要有基于时间序列和时空影响域两种构造方法.Abe和Suzuki(2004)提出了一种基于时间序列构造地震网络的方法,即根据经纬度和震源深度的不同将所求地理区域划分为大小相等的立方体单元,若该立方体单元内发生过地震则将该单元作为地震网络中的一个节点,在时间上相继发生地震的两个节点之间就产生一条边.随后,Baiesi和Paczuski(2005)在此基础上提出加权的地震网络.研究表明地震事件之间在时间和空间上均表现出一定的相关性(王绳祖,张宗淳,2001;徐道一,2001).所以He等(2014)提出了一种基于时空影响域的地震网络构造方法,即根据每次地震的震级大小计算每次地震的时空影响域,如果接下来发生的地震是在它之前发生地震的时空影响域范围内,则将这两次地震所在节点进行连边.使用本方法构造的地震网络具有小世界和无标度等复杂网络的特性(He et al,2014).
本文将地理区域划分为大小相等的单元作为地震网络中的节点,该单元的大小通常与所求震源区的大小具有相当的量级(谢周敏,2011).因此根据Abe和Suzuki(2004)的方法本文选取单元面积为5km×5km.为了使定性分析节点间的关系更为简便,我们将两个节点间的重复边简化为一条边.
基于时空影响域构造地震网络的方法为:假设每一次地震的地震波都在均匀介质中传播的,每次地震发生后,由于应变能的释放,每次地震后都会在空间和时间上产生有限的影响范围,并且震级越大其需要释放的应变能就越大,所产生的影响范围也就越大.时空影响域确定过程如图1所示.可以看出,每次地震后都会在该次地震周围形成一个圆形的空间影响区域S,而对接下来发生的地震产生影响的最长时间就形成了本次地震的时间影响范围T.所以,每次地震都会有一个时空影响域U(T,S)与该次地震相对应.若接下来发生的地震在本次地震的时空影响域内,则视为与本次地震有直接影响,否则视为与本次地震没有直接联系.例如,在tA时刻由于地震A的发生形成了时空影响域U(TA,SA),而在tB时刻地震B发生.由于tB>tA+TA,即地震B不在地震A的时间影响域TA内,所以无论B点是否在A点的空间影响域SA内,均认为地震A对地震B无直接影响.另一种情况,在tC时刻C点发生一次地震,紧接着在tD时刻D点又发生一次地震,由于地震D无论在时间上还是空间上都处在地震C的影响域内,因此视为地震C对地震D有直接影响.
基于时空影响域构造地震网络的重点是如何根据震级的大小确定每次地震的时空影响域.Gardner和Knopoff(1974)给出了震级与影响半径及其与影响时间之间的关系为

图1 基于时空影响域的地震网络三维坐标示意图x轴,y轴和t轴分别表示纬度,经度和时间;两个圆柱体分别表示地震A和C的时空影响域Fig.1 A schematic description of earthquake networks based on space-time influence domain in a three-dimensional coordinate The x-axis,y-axis and t-axis represent latitude,longitude and time,respectively.The two cylinders are space-time influence domain produced by the earthquakes Aand C

式中,M为震级,L为对应震级产生的影响半径,T为对应震级的持续影响时间,a1,a2和b1,b2为常量.由此可知,影响半径和影响时间随震级均呈指数增长的形式.基于时空影响域构造地震网络体现了地震事件之间在时间上与空间上的相关性.由于不同地质结构等其它影响因素,a1,b1,a2,b2的值会因地理区域不同而有所不同.本文通过对Gardner和Knopoff(1974)给出的美国加州地震震级与影响半径和影响时间之间的对应关系,进行最小二乘拟合,结果为lgL=0.122 9 M+0.988 5,lgT=0.457 1 M-0.064 22(0≤M≤6.5),lgT=0.058 66 M+2.534(M>6.5).
2 k-核在地震网络中的应用
k-核是由Seidman(1983)提出的一种用于简化网络拓扑结构的方法,从磁学和卡带过滤到社会网络和蛋白质网络等领域均有广泛的应用.k-核在复杂网络领域的应用由Gkantsidis等(2003)以及Gaertler和Patrignani(2004)提出.其相关定义如下:
定义1 k-核(core):一个网络图的k-核是指反复去掉度数小于和等于k的节点后所剩余的子图(Łuczak,1991).
定义2 核数(coreness):节点的核数表示包含该节点的最深的核,即节点存在于k-核中,但是在(k+1)-核中被移除,则节点的核数为k.节点核数的最大值kmax为网络的最大核数,也称为最高核数(Łuczak,1991).
图2给出了求解节点核数的过程.图中使用了不同类型的封闭曲线来表示不同的核.由于所有节点的度数d>0,则整个图组成了0-核;反复删除度数d≤1的绿色节点,剩余的子图形成了1-核,所以绿色节点的核数为0;然后再删除度数d≤2的黄色节点,剩余的子图形成了2-核,所以黄色节点的核数为1;最后剩下的度数d=3的红色节点的核数为2.
节点的核数并不是由节点的度数唯一确定的,在图2中可以看出,节点A的度数为4,但A点的核数却是0;节点B的度数为3,但B点的核数却是2.所以一个节点的核数不仅与该节点的度数有关,也与该节点在网络中的位置有关.在地震网络中,k-核的一个重要特点即为关于节点的连通性.一个节点的核数越大,则通过这个节点到达别的节点的路径越多,也就是说这个节点影响的节点越多.
美国加州的地震数据信息量巨大,并且地处非常具有代表性的环太平洋地震带,因此许多地震学研究人员都以加州为例来研究地震系统(Abe,Suzuki,2004).本文采用美国加州地震数据中心提供的数据(South California Earthquake Data Center,2014),其中纬度范围为30.0°—39.0°N,经度范围为124.0°—111.0°W,震源深度为0—80km,最大震级为M7.3,震级下限为M0.0.为了展现地震网络节点核数的分布特征,图3给出了我们选取加州1992年地震数据按照节点的时空影响域构造的地震网络,图中不同核数的节点用不同的颜色表示.其中红色表示核数大的节点,蓝色表示核数小的节点,其它颜色表示中间核数的节点.可以看出:核数小的节点在地理位置上比较分散,核数大的节点在地理位置上倾向于聚集在一起;核数小的节点相互之间的联系比较稀疏,核数大的节点之间拥有大量的边.这说明核数大的节点所在位置的地震活动频繁且对别的地震有很大的影响,核数小的节点所在位置的地震发生较少且对别的地震的影响不大.

图2 k-核解析图Fig.2 Sketch of the k-core decomposition for a small graph
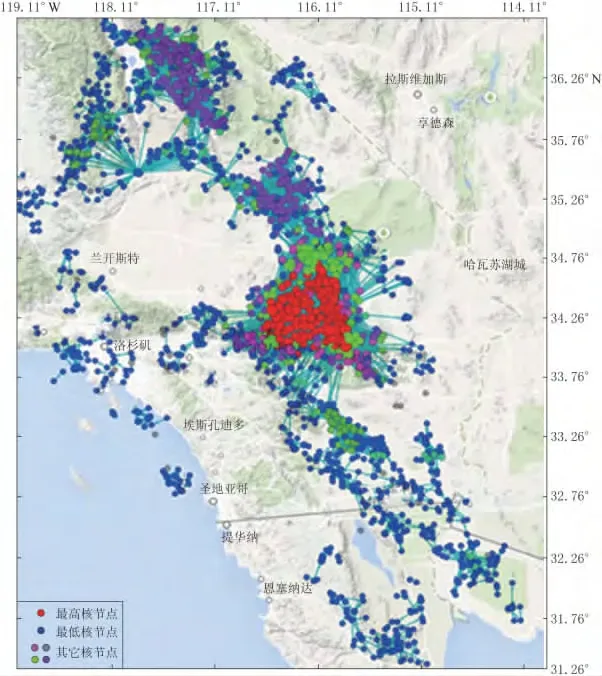
图3 美国加州1992年地震网络的节点核数分布图Fig.3 Distribution of the coreness of earthquake network nodes in California in 1992 Red dots stand for the highest layer nodes,blue dots for lowest layer nodes,and the dots in other colors for the layer nodes between the highest and lowest ones
3 最高核的变化与大地震的关系
3.1 最高核的影响力
由上节定义2可知,由核数为kmax的所有节点及其相应的边组成的子图称为最高核(Dorogovtsev et al,2006),其在整个网络中具有举足轻重的作用.因此研究最高核的节点数和边数等特性,有助于加深对整个地震网络的了解.网络中节点获得的连接总数称为节点的度,网络中所有节点的度的平均值称为网络的平均度.表1给出了美国加州不同时期地震网络的最高核的不同情况.可以看出,虽然最高核的节点数相对于全网所有节点数来说较小,但最高核的平均度却比全网的平均度还高,说明最高核节点的邻居节点特别多,即受最高核节点直接影响的节点特别多.这些最高核节点的邻居节点自身的影响力,也就是这些节点的核数分布情况,如表2所示.可以看出,最高核节点的邻居节点的核数普遍比全网节点的平均核数还要高,说明最高核通过邻居节点的很多路径到达其它节点.
由表1和2可以看出,最高核的节点不仅可以直接影响很多节点,而且受最高核直接影响的节点本身也可以影响很多其它节点,充分说明了最高核的节点可以直接或者间接影响特别多的节点.也就是说,最高核的节点对整个地震网络具有很强的影响力.一次大地震后会引发很多次余震,大地震处于整个地震网络拓扑结构的中心,所以有必要探究大地震的发生与最高核的节点之间是否存在着某种联系.

表1 加州不同时期的最高核Table 1 The highest layer in different periods in California

表2 美国加州不同时期最高核节点的邻居节点的平均核数Table 2 The average coreness of the highest layer’s neighboring nodes at different periods in California
3.2 最高核节点的空间分布特征
最高核节点位于一个地震网络的中心,可以通过地震网络的拓扑结构影响到每一个节点,通过研究美国加州不同时期的地震数据可知,最高核节点在空间上彼此聚集在一起.本文选取美国加州2012年地震信息构造地震网络,根据节点的经纬度显示节点的地理位置,结果如图4所示.可以看出,最高核的节点都位于布劳利这一地区.由于最高核所在位置的地震活动频繁,那么最高核所在的位置是否会发生震级较大的地震呢?我们分别统计了美国加州1992年6月28日M7.3Landers大地震和2010年4月4日M7.2Guadalupe Victoria大地震发生的位置与最高核所在位置的关系,结果如图5所示.

图5 美国加州1992年Landers大地震(a)和2010年Guadalupe Victoria大地震(b)的位置与地震网络中最高核位置的关系图Fig.5 Relationship of the positions of the 1992Landers earthquake(a)and 2010Guadalupe Victoria earthquake(b)with the position of the highest layer of earthquake network in California.The red dots represent the nodes in the highest layer,the black open circle is the node where appears the strong earthquake,the blue open circles represent the nodes of the other earthquake
图5 a给出了美国加州1992年6月28日Landers大地震发生前6个月的所有节点分布,图5b给出了加州2010年4月4日Guadalupe Victoria大地震发生前3个月的所有节点分布.由图5a可以看出:最高核所在的经纬度基本上都集中在34.024°N、116.318°W,发生Landers大地震的经纬度为34.200°N、116.437°W;同样,图5b中最高核所在的经纬度基本上都集中在32.448°N、115.200°W,而发生Guadalupe Victoria大地震的经纬度为32.286°N、115.295°W.由此可以看出,大地震倾向于发生在最高核所在的位置.图6给出了统计美国加州1992年Landers大地震发生前6个月每个月地震网络最高核所在位置与大地震所在位置的距离关系.可以看出,在大地震发生前,随着时间的推移最高核所在的位置越来越接近大地震所发生的位置.这为我们预测大地震发生的位置提供了新的参考途径.
3.3 最高核数在时间上的演化
地震网络的最高核数在一定程度上反映了该地区地震活动的强烈程度,如果某段时间内该地区的地震活动频繁,则地震网络中的节点和边数将增加,最高核数也将相应增加.所以统计地震网络的最高核数可以展现地震活动的强烈程度.图7给出了1992年美国加州Landers大地震和2010年Guadalupe Victoria大地震发生前后的最高核数变化以及加州2011—2013年每个月的最高核数变化.
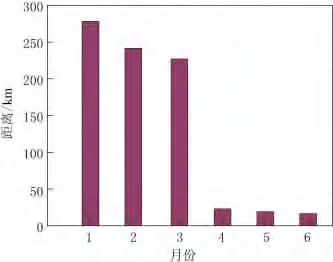
图6 美国加州1992年Landers大地震位置与每个月地震网络中最高核位置间距离的变化图Fig.6 The distance between the position of 1992Landers earthquake and the position of highest layer of every month in California
由图7b可以看出,在没有大地震发生的2011—2013这3年里(最大震级为M5.44),每个月的核数变化不大,每个月最高核数都在6—10的小范围内波动.所以当每个月的最大核数增加时,说明该地区地震活动频繁,可能预示着将有较大震级的地震发生.由图7a可以看出,在1992年的1,2,3月份和2010年的1,2月份,每个月的最高核数都在6—9之间小范围波动,这与2011—2013这3年里每个月的最高核数保持一致.但在1992年的4,5月份,最高核数达到了20和17;在2010年3月份,最高核数竟达到了11.这说明这段时间地震活动比较频繁,与大地震来临前的征兆具有一定的相似性.随后在1992年的6月份和2010年4月份分别发生了Landers地震和Guadalupe Victoria地震,并且这两个月的最高核数均达到了最大值,紧接着每个月的最高核数缓慢减小,最终恢复到没有大地震发生时的稳定值.所以研究大地震发生前最高核数的变化,有助于及时掌握地震发生的一些活动规律,为研究地震的发生规律提供参考和依据.
通过对比美国加州1992年与2010年这两次大地震发生前最高核数的变化可以看出,在1992年Landers大地震发生前两个月,地震网络中最高核数明显上升,而在2010年Guadalupe Victoria大地震发生前一个月地震网络中最高核数才发生少许上升.通过分析这两次大地震发生前的地震信息我们可以看出,在Landers地震发生前两个月发生了M6.1的Joshua Tree地震,它是Landers地震的一次前震,并且该地震引起了超过6 000次的余震(Hauksson et al,1993).因此,造成Landers大地震发生前最高核数发生明显上升的原因可能与大地震的前震有关,这些地震会导致整个地震网络发生层次性变化,这也是造成Landers地震发生前地震网络的最高核数突然增加的主要原因.
4 讨论与结论
本文通过实验发现美国加州1992年Landers和2010年Guadalupe Victoria这两次大地震发生前地震网络中最高核数都会有所增加,但并不是所有的大地震都能引起地震网络的最高核数发生变化.例如美国加州2009年12月30发生M5.8地震,但地震网络中的最高核数并没有明显增加.这可能是由于此次地震并没有引起地震网络的层次性变化,而地震网络的层次性变化是最高核数发生变化的主要原因.所以我们推测地震网络的最高核数的变化不仅与大地震有关,还可能与大地震所处的断裂带等因素有关,我们将在另文中对此进行详细的探究.
本文根据地震事件之间存在时间和空间上的相关性,提出了一种基于时空影响域的地震网络构造方法.通过运用复杂网络的方法研究地震数据的统计规律,然后运用k-核的方法对美国加州的地震数据进行分析,发现最高核具有以下规律:
1)通过对美国加州地震数据组成的地震网络进行k-核解析,发现最高核节点在地理位置上聚集在一起.这说明每个地区的地震都有一个集中在某个地理位置上的地震频发区,其周围的地震都与该地震频发区存在直接或间接的联系.
2)通过分析大地震与最高核之间的位置关系,发现大地震倾向于发生在最高核节点所在的位置,这为我们预测大地震的发生地点提供了一种新的思路.
3)通过对美国加州1992年Landers大地震发生前后的最高核数进行统计,发现有一部分大地震发生前地震网络的最高核数会显著增加.
本文通过对美国加州地震数据的研究提示了大地震在时间和空间上与最高核数之间的关系,这为大地震的短期预报提供了一种新方法.
王绳祖,张宗淳.2001.地震时空影响域、复发间隔和有效孕震时间[J].中国地震,17(4):364--377.
Wang S Z,Zhang Z C.2001.Earthquake-affected time-space domain,recurrence interval and effective preparation time of earthquakes[J].Earthquake Research in China,17(4):364--377(in Chinese).
谢周敏.2011.地震活动的网络拓扑结构和网络动力学行为[J].震灾防御技术,6(1):1--17.
Xie Z M.2011.Network topology and network dynamical behavior of seismicity[J].Technology for Earthquake Disaster Prevention,6(1):1--17(in Chinese).
徐道一.2001.大地震发生的网络性质:兼论有关地震预测的争论[J].地学前缘,8(2):211--216.
Xu D Y.2001.The network features of large earthquake occurrence and some words on the debate of earthquake prediction[J].Earth Science Frontiers,8(2):211--216(in Chinese).
周涛,柏文洁,汪秉宏,刘之景,严钢.2005.复杂网络研究概述[J].物理,34(1):31--36.
Zhou T,Bai W J,Wang B H,Liu Z J,Yan G.2005.A brief review of complex networks[J].Physics,34(1):31--36(in Chinese).
Abe S,Suzuki N.2004.Scale-free network of earthquakes[J].Euro Phys Lett,65(4):581.
Baiesi M,Paczuski M.2005.Complex networks of earthquakes and aftershocks[J].Nonlin Process Geophys,12(1):1--11.
Bottiglieri M,de Arcangelis L,Godano C,Lippiello E.2010.Multiple-time scaling and universal behavior of the earthquake interevent time distribution[J].Phys Rev Lett,104(15):158501.
Dorogovtsev S N,Goltsev A V,Mendes J F F.2006.k-core organization of complex networks[J].Phys Rev Lett,96:040601.
Ferreira D S R,Papa A R R,Menezes R.2014.Towards evidences of long-range correlations in seismic activity[J].arXiv Preprint arXiv:1405.0307.
Gaertler M,Patrignani M.2004.Dynamic analysis of the autonomous system graph[C/OL]∥International Workshop on Inter-domain Performance and Simulation.[2014-04-12].http:∥patrignani.dia.uniroma3.it/papers/files/ASGraphDynamicAnalysis.pdf.
Gardner J K,Knopoff L.1974.Is the sequence of earthquakes in southern California,with aftershocks removed,Poissonian?[J].Bull Seismol Soc Am,64(5):1363--1367.
Gkantsidis C,Mihail M,Zegura E.2003.Spectral analysis of internet topologies[C]∥Twenty-Second Annual Joint Conference of the IEEE Computer and Communications.San Francisco,CA:IEEE:364--374.
Hauksson E,Jones L M,Hutton K,Eberhart-Phillips D.1993.The 1992Landers earthquake sequence:Seismological observations[J].J Geophys Res,98(B11):19835--19858.
He X,Zhao H,Cai W,Liu Z,Si S Z.2014.Earthquake networks based on space-time influence domain[J].Physica A,407:175--184.
Łuczak T.1991.Size and connectivity of the k-core of a random graph[J].Discr Mathemat,91(1):61--68.
Seidman S B.1983.Network structure and minimum degree[J].Soc Networks,5(3):269--287.
Southern California Earthquake Data Center.2014.Earthquake catalogs[EB/OL].[2014-04-12].http:∥service.scedc.caltech.edu/eq-catalogs/date_mag_loc.php.
Taborda R,Bielak J.2001.Large-scale earthquake simulation:Computational seismology and complex engineering systems[J].Comp Sci Eng,13(4):14--27.
