自适应卡尔曼滤波在大坝形变预报中的应用分析

2015-12-14李洪亮时荣钟双

测绘技术装备 2015年1期

李洪亮时荣钟双

（1.河南省测绘产品质量监督站河南郑州 450003；2.河南省遥感测绘院河南郑州 450003；3.河南省基础地理信息中心河南郑州 450003；）

1 引言

大坝形变主要受到水压、温度和时效等环境因素影响[1]，其中，水压和温度具有日周期变化[2]，时效则综合反映了坝体和基岩在多种因素影响下的不可逆形变，是描述大坝长期形变量的重要参考。对大坝位移值隔天采样，可消除水压和温度的影响，而时效具有缓变性，在短时间内可建立速度项的运动模型，利用卡尔曼滤波可以动态估计与预报。

卡尔曼滤波是递推线性最小方差估计的最优估计，整个递推过程由函数方程，观测噪声、状态噪声以及新息决定，在大坝形变监测中，观测噪声和过程噪声受到环境因素影响，处在不断变化中，而标准卡尔曼滤波中，这两者由先验给定，随着滤波的进行是固定不变的，这显然不能反映大坝形变的动态特性，因而标准卡尔曼滤波不是最优的。本文主要从新息序列的两条统计特性出发，引入调节因子[3]和方差补偿[4]分别实时修正观测噪声和过程噪声，充分利用观测数据的隐含信息，构造自适应卡尔曼滤波模型，最后对两组大坝数据进行了处理，比较标准卡尔曼滤波和自适应卡尔曼滤波方法的预报精度，并给出了对比分析。

2 大坝形变预报中的标准卡尔曼滤波模型

在大坝长期形变监测中，时效项是最主要的形变量，在不发生特殊情况下，如地震、山体滑坡，时效项一般呈线性缓变，因而可以对其建立速度项的运动模型，设观测点的状态向量为为位移，v为速度，则其状态模型为:

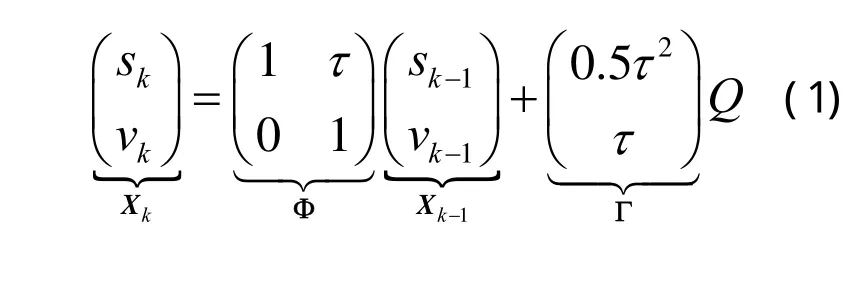
观测值是用仪器（如GPS，机器人全站仪）测得的当期大坝形变位移量Y，那么有如下观测方程:

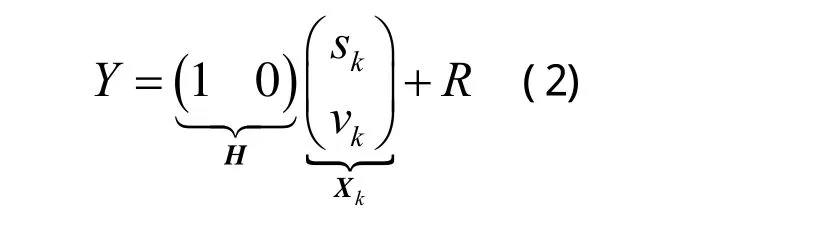
上式中，τ为时间间隔，Q为状态过程噪声，R为观测噪声，在建立了上述状态模型和观测模型后，就可以进行卡尔曼滤波求得每一期的状态。卡尔曼滤波过程如下:

图1:卡尔曼滤波计算过程

只有在当前位移和速度估计精确的情况下，才能得到更高精度的形变预报。卡尔曼滤波是一个状态递推的过程，所有历史信息均被隐含地保留下来，充分顾及了状态时间上的相关性以及所有信息的融合。

3 自适应卡尔曼滤波的构造

在卡尔曼滤波中，过程噪声Q表征了状态转移的不确定性，这种不确定性会随着时间的变化而变化，由于大坝形变受到各种因素影响，这些因素并非一成不变，这导致在大坝形变模型中，各时刻状态转移的不确定度是时变的，应根据实际情况动态地变化。另一方面，观测噪声R也存在同样的情况，它应根据当前观测条件实时的变化。在标准卡尔曼滤波中，过程噪声Q和观测噪声R是事先给定的，在滤波过程中固定不变，从直观上讲，这难以符合实际动态变化情况，尤其在形变突变的情况下，不能很好地自适应描述该过程，导致预报精度较低。在多期观测掌握了足够的数据后，从数据处理角度来看，是可以对观测值和状态的随机过程参数进行验后估计的。

本文采用了一种实时自适应的卡尔曼滤波方法，以新息的统计特性为约束条件，充分利用隐含的历史数据，不断地调整过程噪声Q和观测噪声R，使其能够更好地反映当前的形变动态过程和观测手段的精度情况。

新息被定义为当前实际观测值与预报观测值的差[5]，表述为:

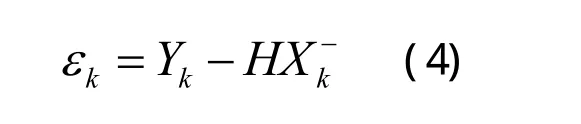
利用线形流形的射影方法可推导出新息序列的两条统计特性[5]:

1）新息序列正交性:

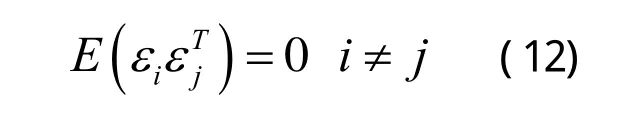
2）新息协方差阵:

新息是历史信息与当前信息的综合表现，当状态模型和观测模型的统计特性准确时，新息满足以上两条统计性质，同样，由以上两条性质可反推模型的统计特性，即Q和R。由于新息是实时计算得到，因而模型的统计特性也能实时的自适应修正。

下面讨论如何根据新息实时修正Q和R。

3.1 调节因子修正R

卡尔曼滤波中，状态的估计由当前观测值和预报状态决定，两者对状态估计的贡献分别由各自的协方差阵决定，即和R，当大时，即预报状态的不确定性大，此时更信任观测值中的信息，反之，当小时，预报状态更准。因此，可动态地调节的大小，间接地影响R对状态估计的贡献，从而间接地修正R，以使估计达到最优。

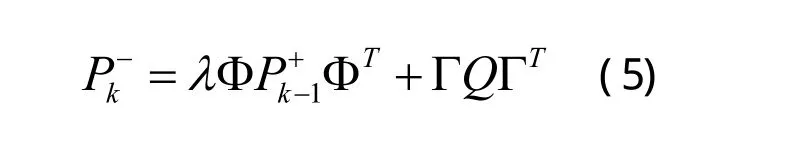
可以证明，利用新息的两条统计性质，可得:

式中，新息ε有当前观测值根据(4)式计算得到，tr为矩阵求迹。

3.1 实时估计修正Q

将性质（2）展开得到:

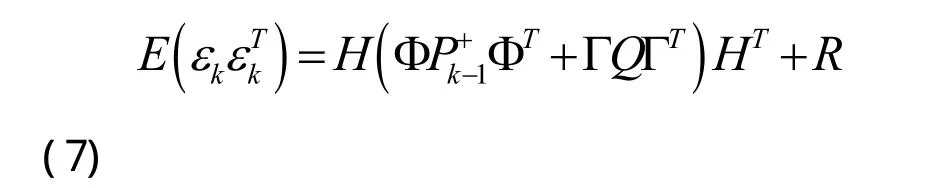
可以看出，如果知道新息和R的统计特性，就能求得Q的统计特性。

假定任意时间段修正的Q为对角阵，记:

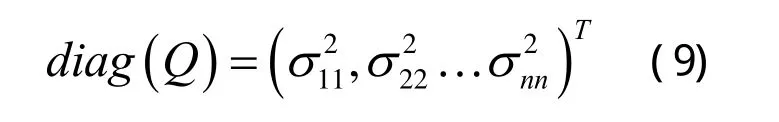
记:

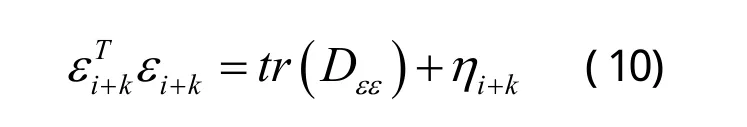
其中ηi+t为零均值随机变量。令

由推导可得:

个以上方程后，就能用最小二乘求得Q的对角元素值。令:

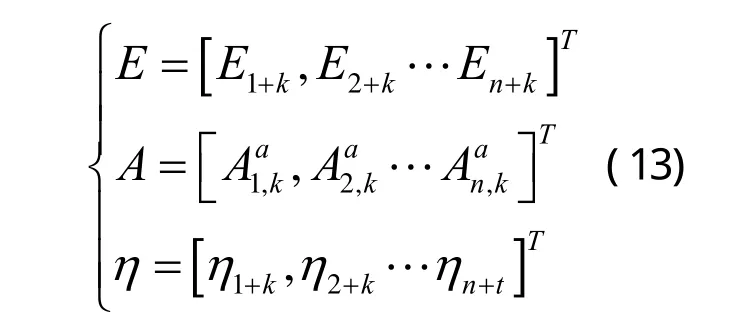
可列得最小二乘方程:

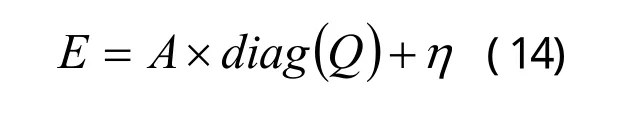
当n大于Q对角线元素个数时，有最小二乘解[6]:

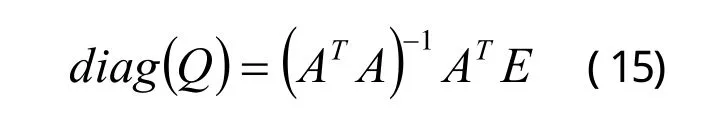
在本文建立的速度模型中，Q为一维，因而不需要多期滤波结果，可以直接利用(12)式进行计算，实时地修正。但为了抵制噪声ηi+t的影响，可以利用多期结果进行最小二乘求解，平滑其它噪声干扰，使得Q的估计更加准确。

4 大坝形变预报应用分析

4.1 数据说明

本文使用两组大坝数据来进行试验分析，以验证在大坝形变预报中，自适应卡尔曼滤波优于标准卡尔曼滤波。

第一组数据使用了我国中部地区某混凝土大坝上布设的水平形变监测点，对其进行了近一个月的连续水平形变监测，观测间隔为1天，共采集了28期的水平径向原始观测值，如图2:

图2:混凝土大坝的水平形变序列

第二组数据为隔河岩大坝坝轴线某监测点在垂向上的形变序列，观测间隔为1小时，共采集了约2个月的数据，如图3:

图3:隔河岩大坝的垂向形变序列

从上图中可以看出，混凝土大坝的形变稳定，趋势比较平缓，因而可以在较长时间间隔连续观测。而隔河岩大坝的形变有较多的突变点，变化复杂，需要在较短的时间间隔观测才能反映其变化情况。

4.2 建立模型

根据第二章，可以建立大坝形变的状态模型(1)式和观测模型(2)式，在滤波估计出当前状态后，利用(3)式可进行下一时刻的形变预报。对于混凝土大坝，从图2中可以发现第二期的速度有突变，因此略去第一期观测值，以二三期观测值计算初值，从第三期开始进行滤波处理并预报，而隔河岩大坝以一二期观测值计算初值，从第二期开始进行滤波处理并预报。

其初始状态如下:

对于两组数据，其它参数均设为一致，如下:

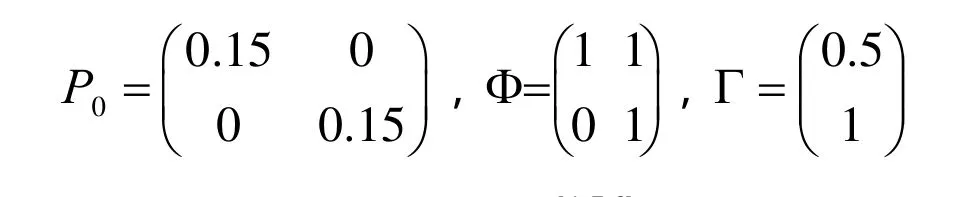
另外，状态噪声取加速度[1,7,8]，其先验值设为，测量噪声先验值设为R=0.1mm，对于标准卡尔曼滤波，在滤波过程中，两者不变，对于自适应卡尔曼滤波，两者随滤波动态情况实时调整。

4.3 结果分析

对每一期大坝形变数据进行滤波后，得到当前最优的形变位移和形变速度，并且以此预报下一期的形变位移。为了比较预报的精度，以实际测得的形变位移为参考，计算预报形变位移的误差。两组数据的标准卡尔曼滤波和自适应卡尔曼滤波的预报误差如下:

图4:混凝土大坝的形变预报误差比较

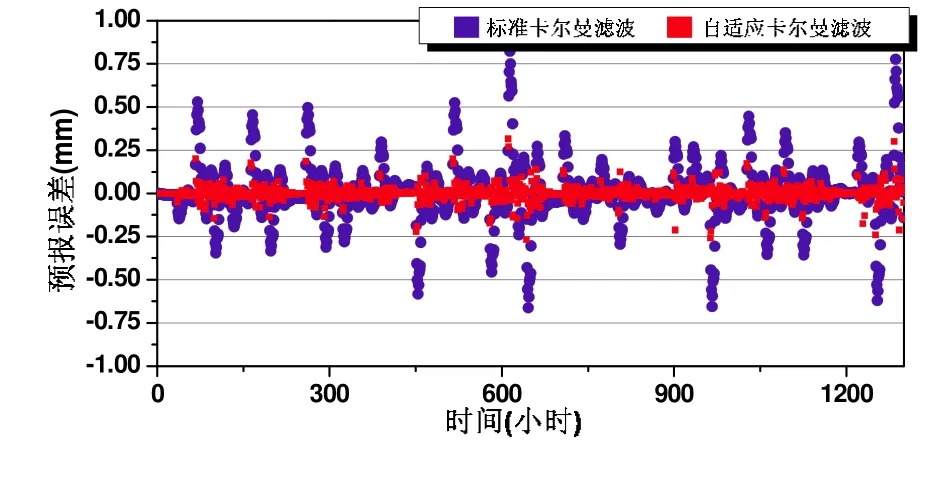
图5:隔河岩大坝的形变预报误差比较

从图中可以明显看出，自适应卡尔曼滤波的预报误差整体小于标准卡尔曼滤波的预报误差。在第一组数据中，自适应卡尔曼滤波预报误差基本在零均值附近上下抖动，未见明显趋势，而标准卡尔曼滤波抖动幅值较大，具有明显的趋势项，这是由于当形变比较剧烈，位移发生突变后，卡尔曼滤波不能迅速进行调整，有一定的滞后性，严重影响了后几期的预报，尤其在第7期到第13期之间，这种影响十分明显，但是自适应卡尔曼滤波能够很好地自适应形变的动态变化，做出迅速的调整，消除当前突变的影响，及时恢复预报精度。该特点在第二组数据中尤为明显，标准卡尔曼滤波在形变位移突变后，出现几期的预报误差都较大的聚集情况，表明卡尔曼滤波不能抑制该影响，造成后续短期内预报的系统偏差。相反，自适应卡尔曼滤波只在突变处的预报误差会稍微偏大（即图中只有一个离散点），而后能迅速恢复预报精度。

下面计算了2组数据2种方法的统计精度，精度提高百分比以及可信度。其中，统计精度为预报误差的RMS；精度提高百分比是以两种方法的预报误差之差大于量测中误差0.1mm的（差值小于0.1mm的预报值，可认为是偶然误差引起，不能判定精度优势），比较两种方法预报更为准确的数量；可信度是以三倍测量中误差作为极限误差，预报误差低于该极限误差的数量。