基于仿射变换的带状影像数据处理技术研究

余咏胜 彭艳丽 易桂轩

（1．武汉市测绘研究院 湖北武汉 430022；2．武汉市规划研究院 湖北武汉 430013）

1 引言

数字正射影像图能真实反映摄影时的地表情况，具有精度高、信息丰富、直观真实等特点，可作为背景控制信息应用于城市规划、土地管理、工程咨询、项目策划等工作。实际生产中经常需要生产单位提供带状航片或卫片影像作为工作底图，特别是近年来无人机遥感技术的普及，小区域、条带影像的数据处理在生产中越来越频繁。由于栅格影像只能按矩形范围存储，常规带状影像通常采取整图拼接后按带状范围的最大外接矩形裁切方式来处理，裁切后一般采用黑色或白色像素填充方式来清除范围外的多余影像数据，该方式处理后输出的成果影像数据量较大，既不方便前期数据处理和影像匀色编辑，也不利于与其它矢量和栅格影像数据的叠加使用。为此，研究既方便带状影像数据生产同时方便后续使用的方法非常必要。

2 仿射变换与影像坐标配准

2.1 仿射变换

仿射变换是空间直角坐标变换的一种，可用于二维坐标之间的线性变换。仿射变换一般可以通过一个3×3的矩阵来表示，设P点的原始坐标为（x,y），变换后P’点的坐标为（x’, y’），其仿射变换的矩阵表示为:

用代数形式表示为:

仿射变换可以通过一系列子变换方式的复合来实现，包括平移、缩放和旋转等。设坐标的平移量为（x0, y0），则平移变换的变换矩阵可表示为:

同样可以推导缩放变换矩阵（4）和旋转变换矩阵（5），其中Rx, Ry分别为x，y方向的缩放因子，θ为逆时针方向的旋转角度。

影像的坐标定位可通过平移、缩放、旋转等仿射变换的复合来实现，根据公式（3）（4）（5），可以得出复合后的变换矩阵为:

由于影像数据按由上至下、由左至右的顺序存储，其y方向与笛卡尔坐标系方向相反，因此必须增加y坐标反向的变换矩阵:

联立公式（6）和公式（7）之后的变换矩阵为:

对于影像数据而言，其缩放因子Rx, Ry对应于影像像素在东西方向和南北方向的地面分辨率，两者取值相同。影像裁切操作是在原有影像的分辨率上进行的，其缩放因子Rx、Ry即影像的地面分辨率R，此时对应的仿射变换矩阵为:

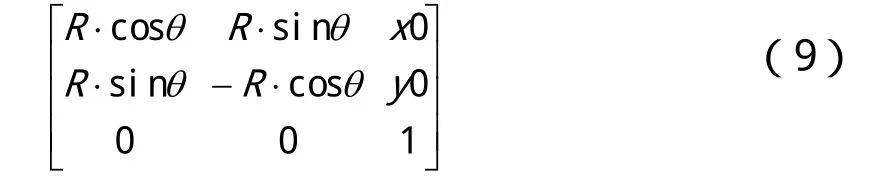
通常情况下，影像数据以矩形方式存储，其旋转角度为0，其仿射变换矩阵可简化为:

2.2 影像文件的坐标配准

矢量数据文件（如shapefile, dwg、dgn等）可以直接存储要素的坐标信息，对于栅格影像而言，其数据按照行列方式依次存储，必须通过配准信息实现影像坐标和地理坐标的转化，配准信息可以通过文件头方式直接存储到影像文件中（如GeoTIFF,IMG, BIL等），也可以存储到独立的ACSII格式的坐标文件中。由于坐标文件方式更易于编辑处理，生产中往往倾向于使用坐标文件方式配准影像的地理坐标。

坐标文件的命名由文件名和后缀名组成，文件名与影像对应的文件名相同，后缀名根据影像文件后缀名的第1个字符和第3个字符再加上字符w构成，不带扩展名或扩展名字符少于3个的可直接增加字符w，如影像文件386525.jpg的坐标文件名为386525.jgw。坐标文件一般由6行数字构成，分别对应于影像仿射变换模型的六个参数，其顺序如表1所示。

表1:坐标文件对应参数

一般而言，如果不考虑影像数据的旋转操作，仅将影像按矩形范围进行存放，影像在水平方向和竖直方向地面分辨率相同，即按简化后的公式（10），表1中的影像坐标参数可以简单归化为表2中对应的坐标参数。其中，第4行数值表示影像分辨率R的负值。

表2:无旋转坐标文件对应参数

3 带状影像的数据处理

本文根据以上影像变换原理，通过Python语言实现带状影像数据的自动裁切和影像配准，裁切后的影像可减少带状矩形范围外的数据冗余。Python是一种支持动态输入的解释型通用编程语言，在ArcGIS中可以通过Python高效地执行数据分析、数据转换、数据管理和地图自动化等操作，通过导入 Arcpy模块可以访问地理处理工具以及其他函数、类和模块，从而创建简单或复杂的工作流程。本文相关程序是以 ArcGIS10.0版本为基础进行二次开发完成。

3.1 处理流程

要实现带状影像的裁切处理，首先应确定带状矩形的中线及两侧距离，据此范围收集相关正射影像数据并对需要处理的影像进行拼接，然后以带状矩形左上角坐标为中心对拼接影像进行旋转操作，此时可以按水平矩形范围对旋转后的影像进行裁切操作，最后根据带状矩形计算裁切影像坐标，完成裁切后影像的地理坐标配准工作。具体实现代码如下:

（1）确定相关参数

先确定带状矩形中线的起止点坐标(x1, y1)、(x2, y2)以及两侧的扩展距离 r，据此计算带状矩形左上角坐标(x0, y0)，相关代码如下:

（2）拼接影像的旋转

利用 Arcpy的数据管理工具Rotate_management()函数可以实现影像的定点旋转操作，影像数据的旋转按指定角度（以度为单位）顺时针进行，负值将按逆时针方向旋转，旋转后的影像保持原有影像的地面分辨率。如果带状矩形范围涉及多幅影像，应在影像旋转前对影像进行拼接处理。为方便后续操作，本文以带状矩形左上角设置为旋转中心进行操作，其中iRas为拼接后的原始影像，裁切影像oRas的内插方式为双线性内插。相关代码如下:

（3）影像裁切

影像旋转后，除旋转中心外其它像素坐标均发生变化，影像裁切必须以旋转中心（即带状矩形的左上角坐标）为基准进行操作。通过数据管理工具中的 Clip_management()函数可以实现栅格数据集的裁切处理，由于带状矩形的左上角坐标和矩形宽度和高度参数已知，据此可以确定裁切范围的四角坐标，相关代码如下:

（4）坐标文件生成

由于影像进行了拼接、旋转和裁切等操作，处理后的影像坐标配准信息随之变化，但ArcGIS软件无法根据该变化更新对应的影像坐标文件信息，必须根据裁切矩形范围通过程序生成对应的影像坐标文件，相关定位参数应根据仿射变换模型进行计算。生成坐标文件的相关代码如下:

3.2 试验结果分析

为验证本文提出的带状影像数据处理的效率和可靠性，本文以武汉市轻轨1号线某段沿线带状影像的数据处理为基础进行了生产性试验。根据相关部门要求，需提供该路段沿线 100米范围内的1:2000比例尺数字正射影像数据作为工作底图，为政府土地开发利用提供基础信息。如图1所示，红色线划为裁切矩形范围的中线，蓝色线划为中线两侧外扩100米之后的裁切矩形，原始正射影像数据的地面分辨率为0.2米。

图1:裁切之前的原始影像

利用本文方法可实现蓝色矩形范围内带状影像数据的自动处理，处理后的结果影像按矩形范围存储，像素数为 6000×1000，影像数据量大小为17.1MB，该影像在非GIS软件中打开为普通矩形影像数据，影像中不存在空白填充区域，在GIS软件中载入该影像时可以根据坐标文件配准到相应的地理位置，如图2所示，在该影像图层下载入其它矢量或影像数据时，位于裁切矩形范围以外空白区域的数据可以正常显示。如果采用常规方式处理该带状影像，通常需要在Photoshop等图像处理软件中对裁切范围以外的影像数据进行清除操作（一般以白色底色填充），该方式处理后的影像像素数为4938×4962，数据量大小为70.1MB，约为本程序成果数据量的4.1倍。此外，常规方式处理的影像在GIS软件中载入后，位于裁切矩形范围以外的矢量或影像数据将被白色填充影像遮挡不能显示。

图2:裁切之后的成果影像

本方法成果影像对应的坐标文件内容如表3所示，第1行至第4行数据是与影像地面分辨率0.2相关的仿射变换参数，其中第1行和第4行数值符号相反，第2行和第3行数值相同，但不是常规坐标文件中的数值0，第5行和第6行为影像左上角像素对应的地理坐标。成果影像的地面分辨率与原始影像的地面分辨率相同，但不能通过坐标文件直接读取，只能通过坐标文件提供数值按仿射变换模型计算相应的地面分辨率。

表3:裁切影像的坐标文件

4 结论

本文以带状矩形为基本处理单元，通过仿射变换模型确定带状影像的地理配准信息，与传统的带状影像裁切方式相比，本方法不需要对带状矩形范围外的数据进行清除处理，不存在数据冗余，可以提高带状影像数据的处理效率，节省数据存储空间，实际操作简单易行，特别是对于线路较长、旋转角接近45°的带状影像数据量减少比例最为明显。对于带状影像的裁切中线为多段折线的情况，只需要在本文方法的基础上进行多次连续裁切即可实现，实践证明该方法高效、可靠，具有很强的实用性。

[1]余咏胜，罗名海，吴克友，尹言军.基于FME的地理国情覆盖要素提取技术探讨[J]地理空间信息，2014(05):01-03.

[2]陈白，王佩，崔彩凤.基于ArcGIS的影像地图制作方法[J]测绘技术装备，2014(03):68-69.

[3]梁秀红，窦龙江，于兴江.仿射变换的应用[J]聊城大学学报(自然科学版)，2013(04):33-35.

[4]赵巍，赵敏，王玉贤，戚娅萍.浅谈影像坐标信息World文件[J]测绘标准化，2010(01):36-38.

[5]林素妆.AutoCAD加载正射影像的实现[J]地理空间信息，2009(05):57-59.

[6]储美华.大比例尺数字正射影像图的制作方法和技巧[J]测绘技术装备，2002(01):14-16.

[7]何斌，马天予等.Visual C++数字图像处理[M]北京:人民邮电出版社，2001:4-20