渗透率的非均质性对CO2地质封存的影响

鲁维丰，张可霓，凌璐璐，郭朝斌

（1. 北京师范大学水科学研究院，北京 100875；2. 北京师范大学地下水污染控制与修复教育部工程研究中心，北京 100875）

渗透率的非均质性对CO2地质封存的影响

鲁维丰1,2，张可霓1,2，凌璐璐1,2，郭朝斌1,2

（1. 北京师范大学水科学研究院，北京 100875；2. 北京师范大学地下水污染控制与修复教育部工程研究中心，北京 100875）

CO2地质封存可以减少化石燃料燃烧排放的CO2量，有效减缓温室效应。储层渗透率可以决定CO2通道的形成，进而改变其在储层中的运移规律，因而是影响CO2地质封存的重要因素。根据研究区基本地质数据、三维地震勘探结果和统计规律确定了渗透率的分布情况，运用储层多相流模拟软件TOUGH2-MP分析了渗透率的非均质性对CO2地质封存的影响。结果表明：（1）渗透率的分布情况对CO2储存量和注入压力的影响很大，相比于均值模型，CO2的注入总量明显减少，到达最大允许压力积聚所需的时间要比均质模型短；（2）在保证注入速率和压力积聚不超过允许最大值的双重要求下，定压和定量两种注入方案都有待改进，建议考虑如人工压裂等工程措施；（3）渗透率的非均质性使得CO2晕呈现出不规则扩散，经过20年的注入，其最大扩散距离约800m，比均质情况下小150m，须做好相应的监测工作。

CO2地质封存；渗透率；非均质性；数值模拟

近年来，煤、石油、天然气等化石燃料的大量燃烧，严重破坏自然和人类生活环境。在排放的温室气体中，CO2气体大约占到总量的65%[1]。未来一段时间内，化石燃料仍将是主流能源。预计到2025年，我国将成为全球最大的CO2排放国[2]。碳捕获和封存（Carbon Capture and Sto rage，CCS）是一项减少人为CO2排放、缓解温室效应的有效措施[3]。在CCS技术中，深部咸水层封存因其巨大的封存能力和相对的安全性，被认为是目前最具前景的一项技术。

国际上开展了大量关于CO2地质封存的研究和实际工程。注入方案、注入率及注入压力对储存容量的影响，CO2的迁移规律等方面都已有很多报道[4～6]，石油工业中对渗透及储层非均质性的研究也相当广泛[7,8]，但缺乏同时考虑各种注入因素与渗透率的非均质性对储存容量影响的系统性研究。而实际野外地质系统基本都具有非均质性，因此探索渗透率的非均质性对CO2地质封存的影响具有非常重要的理论价值和实际意义。

本文以鄂尔多斯深部盐水层CO2地质封存项目为背景，运用数值模拟手段分析了鄂尔多斯砂岩储层的非均质性对CO2注入及封存能力的影响。

1 理论分析

储层非均质性是指储层在形成过程中受沉积环境、成岩作用和构造作用的影响，在空间分布及内部属性上都存在不均匀的变化[9]。近年来，关于储层非均质性的研究越来越多，尤其在定量表征方面[7,10]。渗透率是储层储存CO2的重要影响参数，也是定量表征储层非均质性的典型参数，包括渗透率变异系数Vk、渗透率突进系数Tk及级差Jk。它们的差异性集中反映了储层的非均质性，对CO2运移分布有着显著影响[8]。但这些研究大多集中在石油领域，在如今对CO2地质封存的要求越来越精细的情况下，应该引入储层非均质性的相关计算，使得模拟结果更加精确。

在一定压差下，岩石允许流体通过的性质称为岩石的渗透性，从数量上度量岩石渗透性的参数就叫岩石的渗透率，它反映了储层的渗流能力。模型中储层渗透率的随机分布情况通过TOUGH2软件实现[11]，公式如下：

公式中，k'为修正后的渗透率，k为研究区网格的绝对渗透率（即基准值），本研究取代表层的平均值，m为软件内部自动生成或用户指定的渗透率修正参数，这里根据项目组其他课题提供的地质模型数据进行插值后得到。

当渗透率发生改变时，毛细管压力会根据Leverett相应地发生改变：

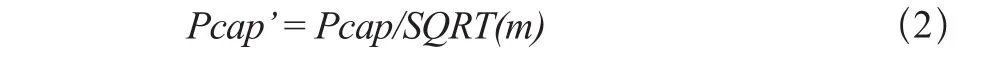
其中Pcap’为转换后的毛细管压力，Pcap为原始毛细管压力，SQRT(m)代表渗透率修正系数的1/2次幂。

地下多相流动质量、能量及达西定律方程见表1。

表1 质能守恒及达西定律方程Table 1 Equation of quality & energy conservation and Darcy's law

2 模型案例

2.1 模拟软件介绍

TOUGH2是非饱和地下水流及热流传输（Transport of Unsaturated Groundwater and Heat）的简称，可模拟一维、二维和三维孔隙或裂隙介质中多相流、多组分及非等温的水流及热量运移，在研究CO2地质封存领域已得到了国际上的认可。此外，它还应用于地热储藏工程、核废料地质处置、饱和/非饱和带水文、地下水中有机挥发性污染物传输以及环境评价和修复方面[12～15]。

CO2储存到深部咸水层中涉及到复杂的H2O/NaCl/CO2多相流过程，同时需要描述并刻画H2O-CO2-NaCl混合物的热力学和热物理性质等。TOUGH2软件中的ECO2N模块能满足这些要求，美国劳伦斯伯克利国家实验室(LBNL)地球科学部设计之初就是为了模拟在咸水含水层中储存CO2这一复杂过程。它可在实验误差范围之内和一定的压力、温度、盐度条件下（P≤600bar；10ºC≤T≤110ºC），进行单相（气相或液相）或多相CO2流体伴随等温或非等温过程的运动模拟，包括指定时间内整个系统的地层压力变化、CO2相变及运移过程[16]。

本研究案例采用TOUGH2-MP/ECO2N进行相关模拟。并行版TOUGH2-MP由LBNL在2008年推出，旨在解决大尺度模拟计算问题，可在多个CPU的计算平台上进行并行计算[17]。

2.2 模型剖分与网格离散

本研究使用Mview软件对网格进行离散。模型的平面范围以虚拟注入井为中心，东西、南北向各取10km。离散后的模型水平方向分辨率范围5～200m不等，关键区域分5个层进行逐步加密，如图1(a)所示；井孔附近生成放射状非结构性网格，如图1(b)所示。这种非规则网格能够更精细地描绘CO2晕在空间的迁移扩散形态。地层垂向范围1680～2275.6m，分为32个子模型层，其中16个砂岩层、16个泥岩层，共设置了13个注入层，各层根据厚度等距剖分，注入地层厚度范围3.2～20.8 m，用于CO2储存的模型层总厚度为116.4m，模型经细化后有62个模型层，其中27个为CO2注入层。按上述规则剖分后，整个模型网格总数约为47(Gridblocks)，链接总数约为140万(Connections)。

图1 模型水平方向网格离散Fig.1 Plan view of the model mesh

2.3 模型主要参数设置

模型选取的主要参数，根据实际场地钻探、室内试验和三维地震获得，其他难以获得的参数依据参考文献，参照表2。模拟过程中毛细压力和相对渗透率的计算使用的是Corey方程和van Genuchten 公式[18]，van Genuchten参数λ取值0.4。

表2 模型水文地质学和热力学参数设置Table 2 Hydrogeological and thermodynamic parameters of the model

选取模型第1注入层和第8注入层为代表层，描述地层渗透率的随机分布情况，见图2。其中，第1注入层的绝对渗透率k取该层渗透率平均值0.5mD，即以0.5mD为基准，第8注入层的固有渗透率以其平均值1mD为基准。

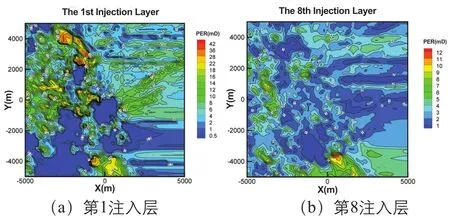
图2 注入层渗透率分布Fig.2 Permeability distribution of the injection layer

2.4 模型初始条件和边界条件

根据重力平衡状态确定整个模型范围内压力分布情况，辅以一些井孔中观测点的压力数据对压力异常分布进行校正。前期可行性研究和物探结果表明注入区为压力相对正常区域，各层地层压力平均系数在0.90～0.96。由地层压力平均系数确定顶层及底层的压力分别为116bar及220bar，利用TOUGH2重力平衡计算功能，得到整个系统的初始压力分布。根据测量到观测点的温度及地温梯度，

确定整个模型地下空间的温度分布，系统的温度分布根据T=0.0319h+10.5（10.5由项目组较早课题提供）进行计算，其中h为地层埋深。虽然温度对CO2的注入效果有一定的影响，但CO2的封存对温度影响有限，因此模型将只考虑恒温状态，可以大大提高模拟效率。

由于模型范围远大于CO2晕扩散范围，将模型四周边界处理为常压力边界。顶底界面与外界的水力联系很小，处理为无流量边界。

2.5 模拟方案

采用一口CO2垂直注入井，模拟注入时间为20年。模型分别采用定压注入和定量注入两种方案，均不采取水力压裂措施。定压方案取1.4P0的基础压力，其中P0为最上方注入点的静水压力，注入点之下的压力以ρCO2gΔh推算，CO2的密度取630kg/m3。定量方案注入速率以10万吨/年设定，注入初期速率较小，前2个月为2.2万吨/年，第3个月增加到4.5万吨/年，从第6个月开始达到10万吨/年。经过计算得出渗透率的非均质条件下模型注入能力、最大压力增加及CO2晕扩散范围等情况。

3 结果和讨论

3.1 注入能力

根据模拟运算得到系统CO2注入总量与注入速率随时间的变化。

如图3(a)所示，经过20年的连续注入，考虑非均质情况下，定量注入方案的总注入量能达到191.49万吨，从第6个月开始年均10万吨；1.4P0定压注入方案的总注入量只能达到55万吨，年均5.75万吨。而均质情况下在1.3P0定压注入的注入总量就能达到年均10万吨。可见，考虑渗透率的非均质性，CO2的注入总量明显减小，这是因为非均质导致的的渗透率空间差异性对CO2运移通道的形成产生影响，导致CO2的流动受到阻碍，从而降低了注入量。

如图3(b)所示，定压方案的注入速率实际上是一个变化值，注入前期系统不太稳定，注入速率起伏较大，从第4年开始呈逐渐增加趋势，至第20年时，达到2.9万吨/年，但距10万吨/年的要求仍较远。

图3 系统CO2注入总量(a)与注入速率(b)随时间的变化Fig.3 The changing of CO2injection volume (a) and injection rate (b) with time in the system

3.2 系统最大压力增加

图4为两种方案的系统最大压力积聚随时间变化图，由中可以看到在整个注入过程中，定量方案产生的最大压力积聚随时间变化曲线起伏明显，达到系统最大压力积聚的时刻大约在第200天，已超过20MPa；定压方案系统中产生的最大压力积聚随着时间的推移逐渐增大，经过10天的CO2连续注入后，基本稳定在6.5MPa。为了满足裂隙封闭压力的需要，确保地层的安全性，系统的最大压力增量要小于最大允许压力（裂隙封闭压力）[19]，而地层裂隙封闭压力通常为静水压力的1～2倍。定压方案按允许的最大注入压力为150%的静水压力考虑[20]，则允许的最大压力积聚不能超过8MPa，即使按200%的静水压力（10.6MPa）考虑，定量方案产生的最大压力积聚也已超过允许值。

另外，该模型中到达最大允许压力积聚所需的时间要比均质模型短，这可能是因为渗透率的变化范围大，导致局部CO2流通不畅，使得压力积聚上升加快。

图4 系统最大压力积聚随时间的变化Fig.4 Maximum pressure build-up with time in the system

3.3 CO2晕扩散范围

模型计算得到第2年和20年各个方案在XY、YZ剖面上的CO2晕分布情况，见图5～图10。其中各图均以CO2气体饱和度等于0.01为基准，XY剖面是选取第1注入层和第8注入层得到，YZ剖面选取X=0m得到。

（1）定压注入方案

由图5～图7可看出，平面第8注入层CO2晕传播距离最远，2年时至150m，平面第1注入层传播至80m，20年时CO2晕最远传播至450m，同样出现在第8注入层，平面第1注入层至200m，停止注入后，CO2晕变化很小。垂向上，CO2基本集中在注入层中，说明盖层具有良好的封闭性。另外，由于受渗透率随机分布的影响，CO2晕形状呈现不规则环形分布。

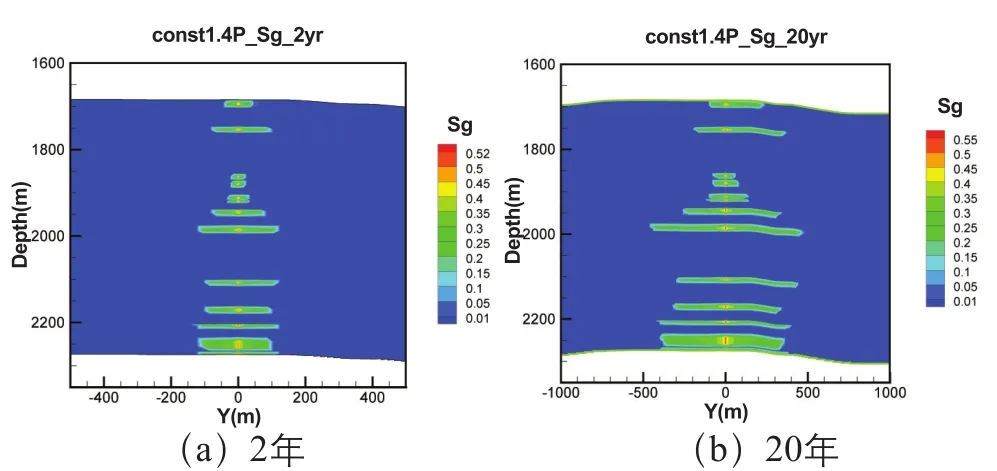
图5 1.4P0方案在YZ剖面上CO2晕分布图Fig.5 CO2plumes distribution in YZ cross-section of the 1.4P0scheme

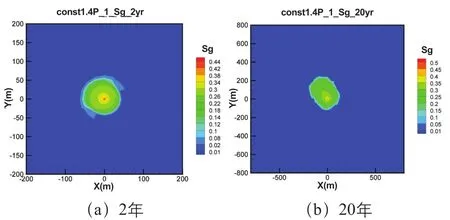
图6 1.4P0方案第1注入层CO2晕分布Fig.6 CO2plumes distribution in the first injection layer of the 1.4P0scheme

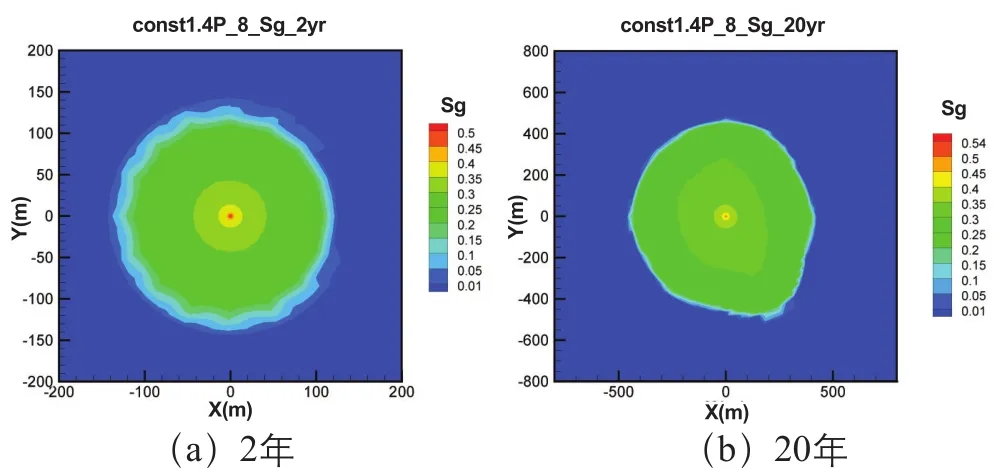
图7 1.4P0方案第8注入层CO2晕分布Fig.7 CO2plumes distribution in the 8th injection layer of the 1.4P0scheme

（2）定量注入方案

由图8～图10可知，2年时CO2晕最远传播至210m，出现在第8注入层，平面第1注入层传播至110m，20年时CO2晕最远传播至900m，平面第1注入层至400m。定量注入方案CO2晕传播范围更远的原因是注入量较大的缘故。同样，由于受渗透率随机分布的影响，CO2晕形状不再是规则环形。

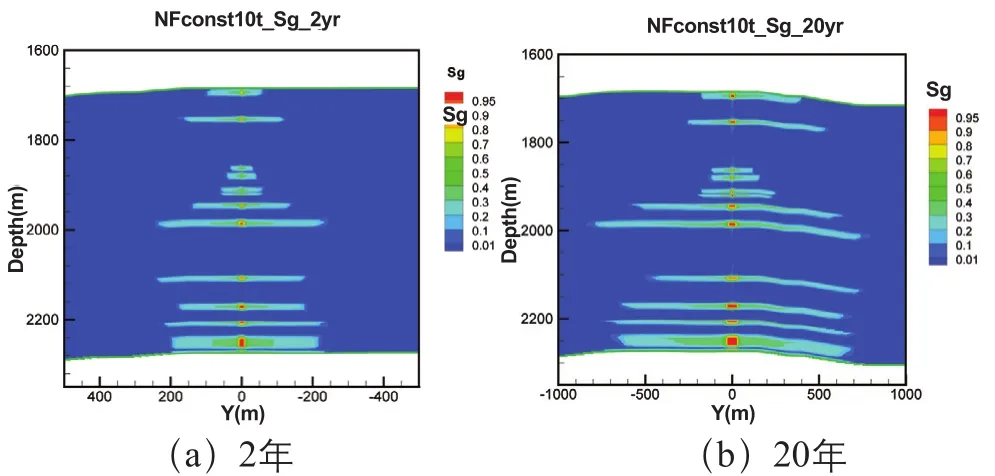
图8 定量注入方案在YZ剖面CO2晕分布Fig.8 CO2plumes distribution in YZ cross-section of the quantitative injection scheme

图9 定量注入方案第1注入层CO2晕分布Fig.9 CO2plumes distribution in the first injection layer of the quantitative injectionscheme

图10 定量注入方案第8注入层CO2晕分布Fig.10 CO2plumes distribution in the 8th injection layer of the quantitative injectionscheme

4 结论

（1）渗透率的分布情况对CO2储存量和注入压力有很大的影响。渗透率会对CO2运移通道的形成产生影响，相比均值模型，非均质模型中CO2的注入总量明显减少，到达最大允许压力积聚所需的时间要比均质模型短。

（2）对比定压、定量两种注入方案的CO2注入量和最大压力积聚可以发现，定量方案的注入量从第6个月开始能达到10万吨/年的要求，但其压力积聚已超过允许的最大值；而定压方案能较好地控制最大压力积聚，使其低于允许的最大值，但年均注入率仅2.8万吨左右，达不到封存要求。在既要保证注入率又要满足压力积聚不超过允许最大值的条件下，两种方案都有待改进。建议考虑采用水平注入井等技术措施，以有效提高存储量和注入能力；在同样注入方式和注入率的情况下，水裂方案能增加CO2注入量，更好地控制系统的最大压力积聚；采用间歇注入方式逐步提高系统注入总量，减缓系统压力积聚。

（3）根据随机分布模型的CO2晕迁移模拟结果，受渗透率随机分布的影响，CO2晕形状呈现出不规则环形分布，经过20年的注入，其最大扩散距离约800m远，比均质情况下小150m，因此须做好相应的监测工作。

References)

[1] 张丽君. 减少温室气体排放的重要手段—二氧化碳的地质储存[J]. 国土资源情报,2001,(12):8-14. Zhang L J. An important means of reducing greenhouse gas emissions: CO2geological storage[J]. Land and Resources Information, 2001,(12):8-14.

[2] Meng K C, Williams R H, Celia M A. Opportunities for low cost CO2storage demonst ration projects in China[J]. Energy Policy, 2007,35:2368-2378.

[3] Ciferno J P, Litynski J L, Plasynski S I. DOE/NETL Carbondioxide capture and storagerd & droadmap[R]. National Energy Technology, 2010.

[4] 李采,张可霓,许雅琴,等. 注入速率对CO2地质储存封存潜力的影响分析[J]. 上海国土资源,2011,32(1):24-27,32. Li C, Zhang K N, Xu Y Q, et al. Analysis of impacts of variation in injection rate on the potential of proposed reservoir for CO2geological sequestration[J]. Shanghai Land & Resources, 2011, 32(1):24-27,32.

[5] 许雅琴,张可霓,王洋. 基于数值模拟探讨提高咸水层CO2封存注

入率的途径[J]. 岩土力学,2012,33(12):3825-3832. Xu Y Q, Zhang K N, Wang Y. Numerical investigation for enhancing injectivity of CO2storage in saline aquifers[J]. Rock and Soil Mechanics, 2012,33(12):3825-3832.

[6] 凌璐璐,许雅琴,张可霓,等. 数值模拟在CO2地质封存示范项目中的应用[J]. 岩土力学,2013,34(7):2017-2030. Ling L L, Xu Y Q, Zhang K N, et al. Application of numerical simulation to pilot project of CO2geological sequestration[J]. Rock and Soil Mechanics, 2013,34(7):2017-2030.

[7] 严科,杨少春,任怀强. 储层宏观非均质性定量表征研究[J]. 石油学报,2008,29(6):870-874. Yan K, Yang S C, Ren H Q. Research on quantitative characterization of macroscopic heterogeneity of reservoir[J]. Acta Petrolei Sinica, 2008,29(6):870-874.

[8] 张岩,李华昌,李允,等. 渗透率随机分布模型在低渗透油藏波及系数研究中的应用[J]. 钻采工艺,2013,36(1):39-42. Zhang Y, Li H C, Li Y, et al. Application of permeability random distribution model in study of low permeability reservoirs sweep efficiency[J]. Drilling & Production Technology, 2013,36(1):39-42.

[9] 杨少春. 储层非均质性定量研究的新方法[J]. 石油大学学报(自然科学版), 2000,24(1):53-56. Yang S C. A new method for quantitatively studying reservoir heterogeneity[J]. Journal of the University of Petroleum, China (Edition of Natural Science), 2000,24(1):53-56.

[10] 文华,孙娜. 一种定量描述气藏储层非均质性的新方法[J]. 特种油气藏,2011,18(1):51-54. Wen H, Sun N. A new quantitative description method of gas reservoir heterogeneity[J]. Special Oil and Gas Reservoirs, 2011,18(1):51-54.

[11] Narasimhan T N, Witherspoon P A. An integrated finite difference method for analyzing fluid flow in porous media[J]. Water Resources Research, 1976,12(1):57-64.

[12] Pruess K, Oldenburg C, Moridis G. TOUGH2 user's guide (version 2.0)[R]. Lawrence Berkeley National Laboratory Report LBNL:46134, Berkeley, CA USA, 1999.

[13] 施小清,张可霓,吴吉春. TOUGH2软件的发展及应用[J]. 工程勘察,2009,37(10):29-39. Shi X Q, Zhang K N, Wu J C. The history and application of TOUGH2 code[J]. Geotechnical Investigation & Surveying, 2009,37(10):29-39.

[14] 王洋,张可霓. 增强型地热系统(EGS)的裂隙模拟方法[J]. 上海国土资源,2011,32(3):77-80. Wang Y, Zhang K N. Modeling approaches for fractures in enhanced geothermal system(EGS)[J]. Shanghai Land & Resources, 2013,34(2):71-75,79.

[15] 郭朝斌,张可霓,凌璐璐. 天然气水合物数值模拟方法及其应用[J]. 上海国土资源,2013,34(2):71-75,79. Guo C B, Zhang K N, Ling L L. Numerical simulation methods and their application to natural gas hydrate exploration[J]. Shanghai Land & Resources, 2013,34(2):71-75,79.

[16] Pruess K. ECO2N: A TOUGH2 fuid property module for mixtures of water, NaCl, and CO2[R]. Report LBNL-57952, Lawrence Berkeley National Laboratory, Berkeley CA USA, 2005.

[17] Zhang K N, Wu Y S, Pruess K. User's guide for TOUGH2-MP: A massively parallel version of the TOUGH2 code[R]. Report LBNL-315E. Lawrence Berkeley National Laboratory, Berkeley CA USA, 2008.

[18] Van Genuchten M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980,44(5):892-898.

[19] US Environmental Protection Agency. Determination of maximum injection pressure for class I wells[R]. USEPA Region 5: Underground injection control section regional guidance #7. EPA, Washington, DC, USA, 1994.

[20] Zhou Q, Birkholzer J T, Tsang C F, et al. A method for quick assessment of CO2storage capacity in closed and semi-closed saline formations[J]. International Journal of Greenhouse Gas Control, 2008,2(4):626-639.

Impacts of heterogeneous permeability on geological storage of CO2

LU Wei-Feng1,2, ZHANG Ke-Ni1,2, LING Lu-Lu1,2, GUO Chao-Bin1,2
(1. College of Water Science, Beijing Normal University, Beijing 100875, China; 2. Engineering Research Center for Groundwater Pollution Control and Remediation, Ministry of Education, Beijing Normal University, Beijing 100875, China)

Geological sequestration of CO2helps reduce the volume of CO2emissions from the combustion of fossil fuels, and may help reduce global warming. The distribution of permeability may determine the formation of CO2migration paths, thereby changing the underground migration of CO2. Permeability distributions in the model area are determined based on hydrogeological conditions observed in Ordos Basin and three-dimensional seismic exploration results at the site. The numerical model is run with TOUGH2-MP software to analyze the impacts of heterogeneous permeability on CO2storage. Model results lead to three main conclusions. Firstly, the distribution of permeability is of great importance to CO2storage capacity and injection pressure. Compared with the homogeneous model, CO2injection volume in the heterogeneous model decreased significantly, as did the time required to reach the maximum allowable pressure. Secondly, injection schemes may need to be improved in cases when there is a required injection rate and maximum allowable pressure build-up. As a consequence, appropriate engineering treatments, such as hydraulic fracturing, are recommended. Third, heterogeneous permeability makes CO2plumes appear irregular and annular in shape. After 20 years of injections, the CO2migration distance reached 800 m in the heterogeneous model, compared with only 150 m in the homogeneous model. This study highlights the needs for proper monitoring of geological CO2sequestration.

CO2geological sequestration; permeability; heterogeneity; numerical simulation

F301.1

A

2095-1329(2015)01-0095-05

2014-10-27

2014-12-06

鲁维丰(1988-),男,硕士生,主要从事地下水环境及多相流体数值模拟研究.

电子邮箱: hhwindlu@163.com

联系电话: 010-53205971

国家能源应用技术及工程示范项目(NY20111102-1);国家十二五科技支撑项目“30万吨煤制油工程高浓度二氧化碳捕集与地质封存技术开发及示范”(2011BAC08B00)

10.3969/j.issn.2095-1329.2015.01.022