基于小波变换的测井多尺度分层研究
2015-12-13雷芬丽
雷芬丽,许 平
(浙江华东工程安全技术有限公司,浙江·杭州 310014)
基于小波变换的测井多尺度分层研究
雷芬丽,许 平
(浙江华东工程安全技术有限公司,浙江·杭州 310014)
测井信号是岩性、地层微观结构、含流体性等各种信息的总和,测井数据是反映地质体地质信息的载体,地层变化主要体现在测井信号的突变点或突变区域中。以某测井的自然伽马曲线为例,提出应用零通小波、模极大值对测井曲线多尺度分析,在不同尺度上定量划分出不同级别的地层界面,分析结果与实际地层界面一致。小波分析为地层的定量划分提供了一种新的思路。
测井曲线;零通小波;模极值;小波变换;多尺度
目前已提出多种测井曲线的计算机自动分层方法,如方差分析法、活度函数分析法、深—频分析法等,但与实际的应用尚有差距,其主要原因是往往一个视觉层次上完成了全部的地层划分工作。而近年来发展起来的小波变换引入了多尺度分析的思想,实现信号分析的时频局部化,能够模拟“由粗略到精细,逐级分层”的人工解释方法,是测井数据时频分析与地质解释恰到好处的数学工具。
近年来研究表明,在各尺度上的边缘能完整且稳定地表征信号,目前基于小波变换的边缘检测,一般有过零检测和模极值检测两种方法。测井数据是反映地质体信息的载体,地层变化主要体现在测井信号的突变点或突变区域中。本文利用小波变换边缘检测方法,应用零通小波、模极大值对测井信号突变点的敏感性和多尺度分析[1],在不同尺度上定量划分不同级别的地层界面,研究该方法的适应性并与实际地质界面作对比分析。
1 小波多尺度分析
1.1 小波变换
设f(t)是平方可积函数,记为f(t)ϵL2(R),φ(t)为母小波,如果φ(t)满足容许性条件
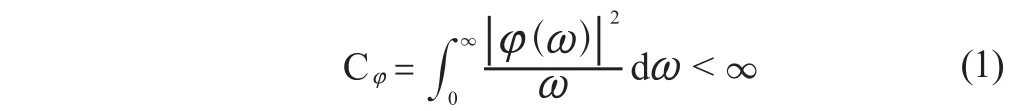
则

称为f(t)的小波变换[2~5]。其中a为尺度因子,决定了信号的采样窗口长度;b为位移因子,决定了逼近信号的时间位置。另外小波变换可以写成卷积形式:

小波的尺度与频率之间关系:尺度a越大表示小波被伸展,时间上观察范围大,对应于信号的低频分量,用低频小波做概貌观察;尺度a越小表示小波被压缩,时间上观察范围小,对应于信号的高频分量,用高频小波可作细致观察。因此,小波变换具有一个灵活可变的时间—频率窗,能在低“中心频率”时自动变宽,而高“中心频率”时自动变窄。
1.2 多尺度分析
测井信号多尺度分析的基本思想是:将待处理的测井信号在不同尺度上小波分解,分解到粗尺度上的信号称之为近似信号,在细尺度上存在,但在粗尺度上消失的信号称之为细节信号,小波分析是连接不同尺度上测井信号的纽带。
对测井信号f(x)离散采样得到离散采样序列f(n)(n=1, 2,…,N),若以f(n)表示信号在尺度j=0时的近似值,记为c0,n=f(n),根据Mallat算法[6,7],测井信号f(x)的多尺度分解可表示为:

式中,cj+1是cj的低频近似,dj+1是cj的高频细节,h(n)和g(n)分别为小波低通和高通滤波器系数。j是小波多尺度分解的层数。根据分解的低频系数和各层高频系数能实现测井信号的重构,测井信号重构表示为:


电子邮箱: lei_f@ecidi.com
联系电话: 0571-56553775
以S地区L1井50.0~150.0m井段自然伽马(GR)曲线为例,选用db4小波对其进行3级分解,多尺度分析结果如图1所示。图中,cA1、cA2、cA3分别表示第一、第二、第三尺度上的低频系数,cD1、cD2、cD3分别表示第一、第二、第三尺度上的高频系数,利用GR曲线3级分解后的小波系数重构GR曲线,其重构最大误差仅为1.48×e-10。

图1 GR曲线正交小波多尺度分析Fig.1 Orthogonal wavelet multi-scale analysis of GR curve
2 测井曲线多尺度分层
测井数据是反映地质体地质信息的载体,地层变化主要体现在测井曲线的突变点或突变区域中。测井信号中突变点或突变区域位置,可能反映在小波系数的过零点上,也可能反映在小波系数的极值点上,目前基于小波多尺度的边缘检测,一般有过零点边缘检测和模极大值边缘检测两种方法。
2.1 零通小波变换边缘检测
设φ(x)为一个光滑函数,且有Φ(x)是该光滑函数的二阶导数:Φ(x)=d2φ(x)/dx2定义:是光滑函数φ(x)关于尺度因子s的伸缩变换。由于

于是得到:
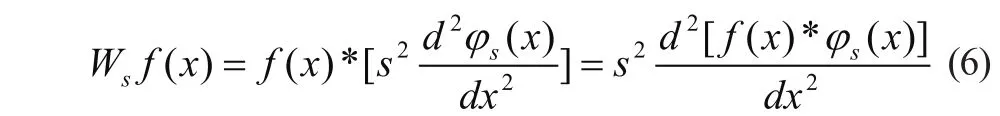
因此,Wsf(x)正比于φ(x),是对测井信号f(x)光滑后所得函数的二阶微分。Wsf(x)的零点位置对应于f(x)*φs(x)的拐点。利用小波变换的零点位置可以确定测井信号的突变点,测井信号的突变一般反映了地层岩性和物性的突变点,所以可以运用测井信号的小波变换的零点位置来检测地层岩性和物性的突变点。
利用零通小波对测井曲线多尺度边缘检测的步骤:
(1)选择合适的小波基函数对测井曲线进行小波变换,为保证检测有效,小波基应是某一光滑函数的二阶导数。
(3)根据步骤(2)中求得的零通点进行地层多尺度分层。
2.2 模极值边缘检测
设φ(x)为一个光滑函数,且有Φ(x)是该光滑函数的一阶导数:

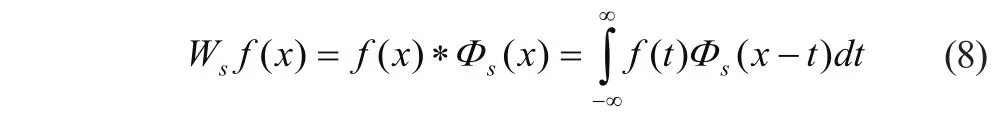
基于模极大值的测井信号多尺度边缘检测的步骤:
(1)选择合适的小波基函数(小波基应为某一光滑函数的一阶导数)对测井曲线进行小波变换,得到一系列小波系数值Wsf(1),Wsf(2),…,Wsf(n);
(2)计算最佳尺度下的模极值点。确定一个阈值E,对i=0,1,…,n,若满足以下二个条件:①Wsf(i)≥E;②Wsf(i)在i点处取模极大值且利普希茨指数(Lipschitz)α>0;那么i点就是信号在尺度s下的一个突变点。
(3)利用尺度s下的模极值点i进行地层多尺度分层。
3 实际资料应用
以S地区L1井50.0~150.0m井段自然伽马(GR)曲线为例,分别应用零通小波变换和模极值的测井曲线多尺度边缘检测,定量划分地层。
Mexihat(墨西哥草帽小波)是高斯函数的二阶导数,墨西哥草帽小波的形状与测井曲线十分相似,可最大程度地突出测井信号,因此本文采用该小波基对实际GR曲线进行处理。图2为利用零通小波对GR曲线进行多尺度边缘检测从而划分地层的过程,从图中可以看出,零通小波变换用于测井曲线分层具有良好效果,与实际岩性柱基本吻合。随着小波尺度的增大,所检测突变的规模也逐渐增
大,划分的地层规模由单岩层到岩层组的组合。
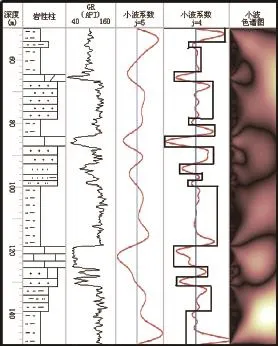
图2 零通小波用于测井多尺度分层Fig.2 Multi-scale demarcation of stratigraphy using zero crossing wavelet
高斯小波是高斯函数的一阶导数,在信号与图像的边缘提取中有重要的应用,因此我们对L1井50.0~150.0m井段自然伽马(GR)曲线利用高斯小波进行基于模极值的测井多尺度分层,图3为模极值测井多尺度分层综合成果图。从图中看出:小波系数曲线上负极值点对应于测井曲线的上升沿,正极值点对应于测井曲线的下降沿;极值点幅度值随尺度变化反映了测井曲线的边缘特性,幅度值较小对应于测井曲线较缓边缘,幅度值较大对应于测井曲线较陡边缘。小波系数色谱图上颜色由亮到暗代表小波系数从高到低,模极值点正好对应于色谱图上亮色区中心位置。利用模极值边缘检测法划分地层,界面位置准确,与地层岩性界面有很好的对应。

图3 模极值测井多尺度分层Fig.3 Multi-scale demarcation of stratigraphy using modulus maxima
4 结论
(1)根据小波多尺度分析理论,对测井曲线进行多尺度分析,将一维的测井信号变换到二维的时间—频率(尺度)域,使其内部的能量聚集与分布得以展示,从而在复杂多变的原始信号中提取原始测井数据所不能体现的信息。
(2)零通小波变换、模极值边缘检测方法具有指示曲线拐点位置和多尺度分析的优良特性,运用零通小波、模极值边缘检测方法划分地层界面位置准确,并且可以选择适当的尺度因子实现不同级别层序地层界面的定量划分,是传统研究方法的有效补充,可以推广至工程应用中。
(3)零通小波检测容受噪声干扰,不如模极值检测稳健;模极值检测不仅能够检测边缘,而且还能够指示边缘的性质,但需要设置适当阈值,若阈值选择不合适可能会造成边缘粗化,定量划分的精度降低,而过零检测在某种程度上是自适应的,不需要设置阈值。
References)
[1] Veniste A, Nikoukhah R, Willsky A S. Multiscale system theory[C]//Proceedings of the 29th IEEE conference on decision and control. 1990:2484-2487.
[2] 房文静,范宜仁,李霞. Morlet小波用于测井沉积旋回多尺度特性研究[J]. 物探化探计算技术,2007,2(2):109-111. Fang W J, Fan Y R, Li X. The multi-scale characteristic study of sedimentary cycle in well logging data using morlet wavelet[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2007,2(2):109-111.
[3] 李霞,范宜仁,房文静,等. 测井多尺度分析方法用于层序地层划分研究[J]. 新疆地质,2006,24(4):454-457. Li X, Fan Y R, Fang W J, et al. Research on the demarcation sequence stratigraphy using multiscale analysis method of well logging[J]. Xinjiang Geology, 2006,24(4):454-457.
[4] 雷芬丽,许平,程武伟,等. 小波分析在测井数据融合处理中的应用[J]. 上海国土资源,2013,34(4):87-90. Lei F L, Xu P, Cheng W W, et al. Application of wavelet analysis for multi-scale fusion of well logging data[J]. Shanghai Land & Resources, 2013,34(4): 87-90.
[5] 于继锋,李增学. 测井数据小波变换及其地质意义[J]. 中国矿业大学学报,2003,32(3):336-339. Yu J F, Li Z X. Wavelet transform of logging data and its geological significance[J]. Journal of China University of Mining & Technology,2003,32(3):336-339.
[6] Mallat S G. Multiresolution approximation and wavelet orthonomal bases[J]. Transactions of the American Mathematical Society, 1989,315(1):69-88.
[7] 陈正星. 小波分析算法与应用[M]. 西安:西安交通大学出版社, 1998. Chen Z X. Wavelet analysis algorithms and its applications[M]. Xi'an: Xi'an Jiaotong University Press, 1998.
Demarcation of stratigraphy using multi-scale well logging based on wavelet transform
LEI Fen-Li, XU Ping
(Zhejiang Huadong Engineering Safety Technology Co., Ltd., Zhejiang Hangzhou 310014, China)
The logging signal is the summation of lithology, stratigraphic structure, fluid properties, and other information. The well logging curve contains the geological information of geological bodies, and changes in formation are reflected in sharp or gradational boundaries between different logging signals. Taking the gamma ray curve of a well log as an example, this paper presents a multi-scale analysis of the logging curve applying a zero-crossing wavelet and modulus maxima. Quantitative classifications of different stratigraphic interfaces are made at different scales, and the results are consistent with the actual boundaries of the formations. Wavelet analysis constitutes a new method for quantitative stratigraphic demarcation.
well logging curve; zero crossing wavelet; modulus maxima; wavelet transform; multi-scale
P631.8
A
2095-1329(2015)03-0076-04
2014-07-05
2014-08-14
雷芬丽(1983-),女,硕士,工程师,主要从事海洋物探研究.
10.3969/j.issn.2095-1329.2015.01.018
