并行传输线共模泄漏的等效场-线耦合数值模型

郁 滨 方 哲 周长林

1 引言

电子信息设备采用并行结构传输线互连时，传输线间耦合串扰产生的共模电流会激发显著的电磁信息泄漏发射，极易产生敏感数据的信息泄漏问题[13]-。因此，针对并行传输线间耦合串扰进行研究，对定量分析传输线共模电磁泄漏具有重要意义[47]-。

并行传输线耦合串扰研究的典型方法是建立线-线耦合形式模型进行解析求解[810]-。文献[9]采用解耦传输线方程方法给出传输线耦合串扰的解析解，但该方法很难求解被扰回路沿线任一点的感应电压和电流分布，也难以求解传输线有损耗和非均匀等情况的耦合。文献[10]借助积分方法，建模求解出被扰回路沿线任一点的感应电压和电流分布，但针对较复杂耦合情形该方法仍难以实现解析求解，同时模型的积分形式过于复杂，不利于计算求解。

针对传输线损耗和介质非均匀等复杂情形，数值方法采用场-线耦合形式模型取得了良好的计算效果[1114]-。文献[11]利用时域有限差分（Finite-Difference Time-Domain, FDTD）方法给出PCB迹线间电场和电势的数值计算模型，但该方法未对传输线间感性和容性场-线耦合机制进行深入研究，也未能给出传输线耦合串扰的数值计算模型。文献[13]借助数值仿真方法建立了多导体传输线耦合串扰的电路模型，可以有效模拟均匀和非均匀场对多导体传输线的耦合串扰。然而，模型中的入射场源为外部场，故该方法并不适用于传输线间耦合串扰的数值计算。

实际并行结构传输线尺度及相互间距离都较小，常规FDTD网格尺度往往存在耦合计算精度过低的问题。而文献[15]提出的亚网络FDTD方法可用来模拟比常规网格尺度小的结构，其较常规网格方法相比具有更高的计算精度，也保持了较好的收敛性。因而，采用亚网格FDTD方法来进行并行传输线场-线耦合数值分析更为适合。

因此，本文拟在传输线间感性和容性场-线耦合机制研究基础上，借助亚网格FDTD方法，建立并行传输线的等效场-线耦合数值模型，进一步利用数值模型对并行传输线耦合共模电磁泄漏进行模拟分析，并在半电波暗室环境下测试并行传输线辐射泄漏发射，以验证数值模型对共模电磁泄漏的模拟计算结果。

2 并行传输线耦合串扰机制研究

在弱耦合条件下，由线-线耦合模型分析可知，并行传输线间耦合串扰包括传输线互感和互容引起的感性耦合和容性耦合。在线-线耦合模型中，感性耦合由传输线间互感系数定量分析，由互感系数产生原理，可进一步探究感性耦合的场-线激励机制，其原理如图1所示。

图1 感性耦合场-线激励模型

据图1所示感性耦合的场-线激励机制，可得并行传输线等效场-线耦合定理1。

定理 1 主扰回路电流J在周围空间产生的磁场H为并行传输线感性耦合的激励磁场。

证明 主扰回路Al上电流为（,）J x t，其激发产生磁场H，根据安培环路定理有

取被扰回路lB沿线一点A，可知A处的磁场会在其截面S产生磁通量φA。由式（1），当电流J（ x, t）连续变化时，A处磁场 HA不断变化，截面S磁通量φA亦随之变化。据法拉第电磁感应定律，磁通量φA变化会在A处感生出电动势 UL和电流 IL：

至此，主扰回路电流变化激发的磁场在被扰回路上激励产生耦合电压和电流。 证毕

容性耦合在线-线耦合模型中则由传输线间互容系数定量计算，对并行传输线间由互容系数引起的容性耦合过程进行分析，以探究容性耦合的场-线激励机制，其原理如图2所示。

图2 容性耦合场-线激励模型

由图2示传输线耦合电容原理，可得并行传输线等效场-线耦合定理2。

定理 2 耦合电容 Cm电荷聚集产生的电场E为并行传输线容性耦合的激励电场。

证明 主扰回路lA上取A点和 B点，电势分别为φA和φB。在耦合电场E作用下，A点和B点将分别在被扰回路lB的C点和D点产生电势φC和φD。两组电势满足如下关系：

考察Al和Bl上的电势降ABU 和CDU ，结合式（3），可知ABU 和CDU 满足如下关系：

由式（4）知，主扰回路电势降通过耦合电场在被扰回路激励产生耦合电压和电流。 证毕

3 并行传输线等效场-线耦合数值模型

3.1 感性耦合的等效场-线耦合数值模型

采用3维亚网格对并行传输线进行划分，建立感性耦合的等效场-线耦合亚网格FDTD数值模型。根据定理1，取Bl上任一点A，讨论磁通量变化在A点产生的耦合电压。如图3所示，对被扰回路沿线A点处的xOz剖面进行亚网格FDTD分析。

图3 被扰回路xOz剖面亚网格FDTD求解图

在图3中，点A和点B为亚网格z轴方向的相邻点，其坐标分别为（,）i k和（,1）i k+。以A点为中心取一个完整亚网格S，设通过亚网格S的磁通量为AφΔ，则对AφΔ有

耦合磁场H在A点产生的耦合电压为U（ i, k），由法拉第电磁感应定律，U（ i, k）满足：

结合式（5）和式（6），在等效场-线耦合数值模型中，时间步长为n时，主扰回路lA在被扰回路lB上A点产生的耦合电压 Un（i, k）满足差分式：

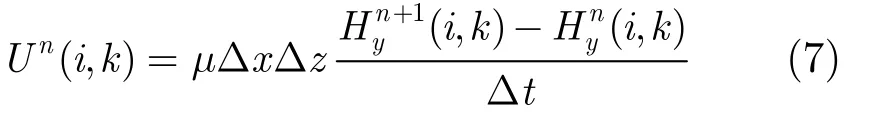
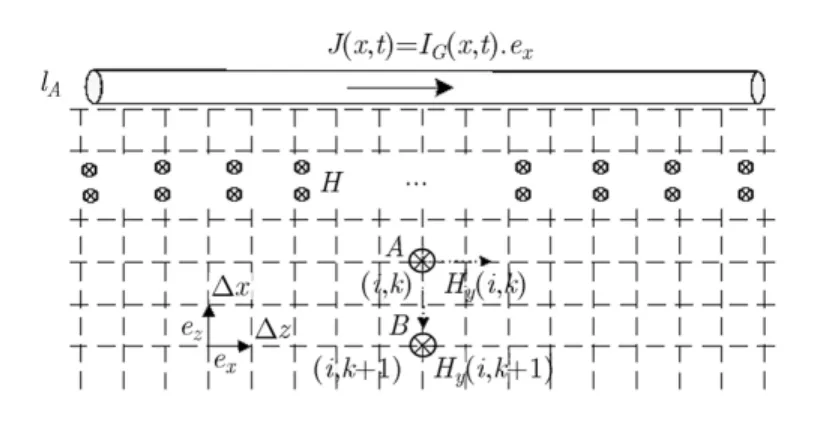
图4 耦合磁场亚网格FDTD数值求解图

据图4进行亚网格FDTD分析，由式（1），可知耦合磁场H满足：

将式（8）展开，分析耦合磁场H矢量各分量值，可得

由安培环路定理，磁场H的z轴方向磁场分量Hz为零，将式（9）表示为差分形式可得

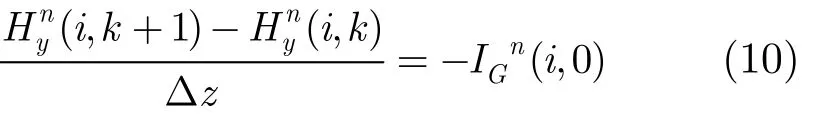
由差分式（10），进一步联立差分式（7），可求解被扰回路l上A点耦合电压 Un（i, k）。

B

3.2 容性耦合的等效场-线耦合数值模型

在感性耦合3维亚网格划分基础上，建立容性耦合的等效场-线耦合亚网格 FDTD 数值模型，选取xOz剖面进行FDTD数值分析，示意图如图5所示。

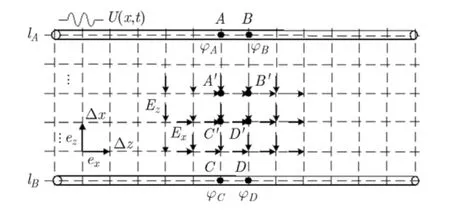
图5 容性耦合xOz剖面亚网格FDTD分析示意图

如图 5所示，主扰回路Al上A点和B点电势分别为Aφ和Bφ，在耦合电场作用下，被扰回路Bl上C点和D点分别产生电势Cφ和Dφ。选取AB和CD段之间亚网格A'B'C'D'，其容性耦合的等效场-线耦合亚网格FDTD数值求解模型如图6所示。

图6 亚网格A'B'C'D'的场-线耦合分析图

在图6中，设A'点坐标为 （i, k），亚网格A'C'边中点处存在 z轴方向的电场分量 Ez（ i, k + 1 /2），同时A'C'边中点处 x轴方向的电场分量为 Ex（ i+ 1/2,k）。

由亚网格FDTD方法，取n倍时间步长，电场分量 Ez（ i, k +1/2） 和电势 φ（i, k ）,φ（ i , k+ 1 ） 之间满足差分式（11）。

由定理 2，只考虑亚网格 z轴方向电场分量Ez（ i, k+1/2）引起的耦合。由z轴方向差分式（11），可得容性耦合电势求解差分式为

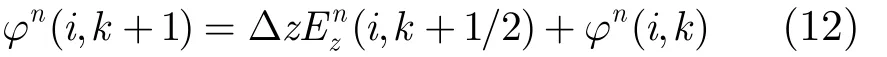
利用式（12）求得C'点和D'点电势φ（i, k+1）和φ（ i + 1 ,k + 1 ） ，进一步求解得到耦合电场 Ez（ i, k+ 1 /2） 在C'点处产生的耦合电压 U （ i, k + 1 ） 为

4 数值模型求解及耦合正确性分析

4.1 数值模型边界条件与求解

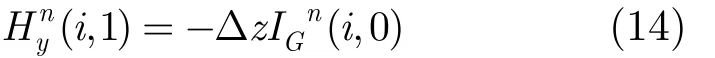
如图3所示，l上坐标（i, k）点耦合电压为Un（i,Bk），设lB上边界 eU和下边界 eD间包含m个亚网格，被扰回路x=i处耦合电压为Un（i），则可以确定数值模型计算区域的截断边界为

联立式（14）和式（15），感性耦合亚网格 FDTD数值模型的边界条件得以确定。此基础上，联立数值模型差分式（7）和式（10），可求解感性耦合的等效场-线耦合数值模型。

设坐标（0,0）点的电势为零参考电势，可得容性耦合截断计算区域的边界条件之一为

如图6所示，设lA和lB间包含n个亚网格，耦合电场 Ez（ i, k）作用下被扰回路坐标 （i, n） 和 （i+1,n）点分别产生耦合电势φ（i,n）和φ（i+1,n）。此时，容性耦合截断计算区域的边界条件为

联立式（17）和式（18），容性耦合亚网格 FDTD数值模型的边界条件得以确定。同理，联立数值模型差分式（12）和式（13），最终容性耦合的等效场-线耦合数值模型求解为

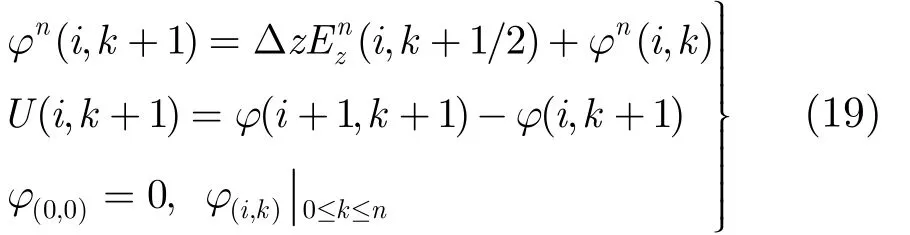
考虑存在非均匀介质的情形，在亚网络FDTD步长单位内，确定等效场-线耦合的激励场 Hn（i, k）

假设一段并行传输线的特性阻抗 Z = 1 00Ω，线长 L = 0 .5m，单线半径 r = 1 mm，双线轴心距离 d = 4 mm。在主扰回路端接匹配负载，考虑如下

4.2 数值模型耦合正确性分析

两种被扰回路端接负载情形：（1）被扰回路始端短路、终端开路；（2）被扰回路始端开路、终端短路。

针对此算例，利用等效场-线耦合数值模型亚网格FDTD算法，当传输线工作在低频范围时，可以计算得到（1）, （2）两种情形的被扰回路感性耦合电压。进一步利用文献[8]Mihailov模型和文献[10]积分模型进行验证计算，可得3种模型耦合求解模拟对比分析图7。

如图7所示，针对（1）, （2）两种情形，L3和 L4为等效场-线耦合数值模型的数值计算曲线， L5和 L6为Mihailov模型的解析求解曲线，L2和 L1为积分模型的积分求解曲线。

比较数值模型计算曲线 L3,L4和积分模型求解曲线 L2,L1，可知数值模型和积分模型及 Mihailov模型求解曲线间存在斜率差Δk。由感性耦合等效场-线耦合数值模型，被扰回路耦合电压 Ux和主扰回路电压 Ex存在斜率关系： Ux= Knum，由积分模型及 Mihailov模型计算， Ux和 Ex存在斜率关系：Ux= Kanc。可知，图中数值模型计算曲线和积分模型及 Mihailov模型求解曲线间斜率差满足：Δk =Knum-Kanc，即此斜率差Δk由计算误差引起。

通过数值模型和已有模型耦合计算的比较分析可知，本文等效场-线耦合数值模型求得的计算结果与典型方法相一致，同时数值模型的求解形式更为简洁，便于计算实现。

5 数值模型共模泄漏模拟及实验分析

以第 4.2节并行传输线耦合算例为例，假设主扰回路上的信号源V为梯形方波信号，峰值为 1 V，宽为30 ns，上下边沿为5 ns。利用等效场-线耦合亚网格FDTD模型，将耦合共模电流J（ x, t）作为等效辐射天线激励源，可得到共模电磁泄漏辐射的近、远场时域波形[16]。

利用坐标系变换，由等效辐射天线模型可得共模电磁泄漏辐射直角坐标系z向电场的近、远场时域解（t）和（t）分别为

取被扰回路的z向距离 d = 0 .125 m和d=10 m，利用亚网格 FDTD算法和等效辐射天线模型，可得并行传输线共模电磁泄漏的时域近区场和远区场模拟仿真波形如图8所示。

如图8示，模拟近区场时域波形保留了主扰回路激励脉冲的基本形状，在信号的上下边沿处存在较大强度电磁辐射，其原因是上下边沿处的谐波分量产生了幅值较强的电磁辐射。模拟远区场时域波形已不具备激励脉冲基本形状，仅在上下边沿由谐波分量产生了较强电磁辐射，且随着距离d的增大，远区场时域波形的带宽和能量均有所降低。

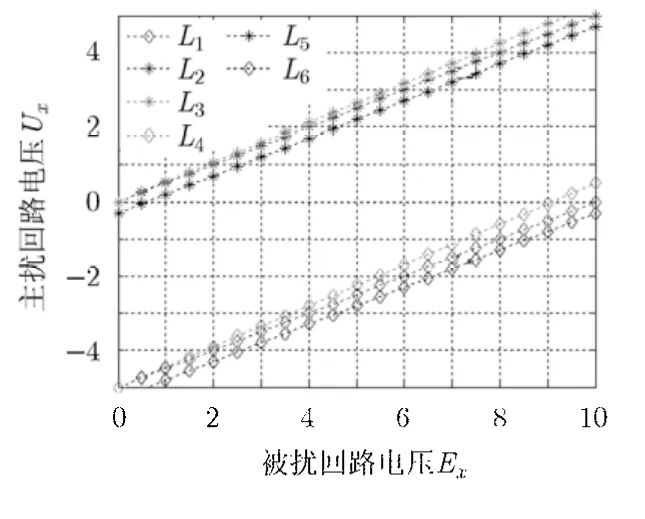
图7 3种模型耦合计算对比分析图

图8 数值模型模拟传输线辐射时域波形图

由亚网格FDTD数值模型求解方程组式（16）和式（19），进一步定量分析耦合共模电磁泄漏发射水平。被扰回路耦合电压 Ux和主扰回路电压 Ex存在线性关系：Ux= Knum+ Dnum，其中，Knum为斜率，Dnum为截距。

分析可知耦合电压 Ux即为共模电磁泄漏辐射相对无耦合电磁泄漏辐射的激励增量，结合式（20）和式（21），可求解共模电磁泄漏辐射发射的幅值增量Δ（E, H）。

为验证理论分析的定量结论，在半电波暗室进行传输线频域实验测试。实验选取的并行传输线由工作频率为30 MHz的串行同步传输线和直流电源线并行组成，实验测试主设备为TEMPEST接收机和10 kHz～ 200 MHz天线组，辐射发射实验测得频域图谱如图9所示。

比较图9（a）和图9（b）中1X 处的电磁泄漏发射幅值可知，在传输线同步信号的中心频率30 MHz处，共模电磁泄漏较无耦合情形的频谱发射幅值增加25dB V/mμ。根据共模电磁泄漏发射定量分析式（22）可知，图9（a）相对图9（b）的幅值增量（）,E HΔ由亚网格FDTD数值模型求解的耦合因子numK 和numD决定，numK 和numD 的微小变化导致了共模电磁泄漏发射的幅值增加，因而由传输线间耦合串扰引起的共模电磁信息泄漏更为显著。

6 结束语

在并行传输线感性和容性耦合等效场-线激励机制研究基础上，本文提出并行传输线等效场-线耦合亚网格FDTD数值模型，模型便于实现计算求解，且更适合于非均匀介质等复杂情形的耦合计算。利用数值模型，可对并行传输线共模电磁信息泄漏进行模拟仿真，结合半电波暗室频域实验表明，本文模型可准确描述并行传输线共模电磁信息泄漏发射规律。

图9 半电波暗室传输线辐射测试频谱图

[1] Tarateeraseth V, Kye Y S, Canvero F G, et al.. Systematic electromagnetic interference filter design based on information from in-Circuit impedance measurements[J].IEEE Transactions on Electromagnetic Compatibility, 2010,52（3）: 588-598.

[2] Yuichi H, Kouhei O, Takaaki M, et al.. Influence of PCB and attached line of hardware on electromagnetic （EM）information leakage[J]. IEEJ Transactions on Fundamentals and Materials, 2012, 132（2）: 173-179.

[3] Djordjevic A R, Tosic D V, Zajic A G, et al.. Temporal leakage in analysis of electromagnetic systems[J]. Antennas and Propagation Magzine, 2012, 54（6）: 92-101.

[4] Su Ch Y and Hubing T H. Imbalance difference model for common-mode radiation from printed circuit boards[J]. IEEE Transactions on Electromagnetic Compatibility, 2011, 53（1）:150-156.

[5] Hoa C Y, Chena K S, and Hornga T S. Prediction of common-mode radiated emission from PCB using vector network analyzer with a bulk injection current probe[J].Journal of Electromagnetic Waves and Applications, 2012,26（16）: 2121-2129.

[6] Yuichi H, Naofumi H, Takaaki M, et al.. Evaluation of information leakage from cryptographic hardware via common-mode current[J]. IEICE Transactions on Electronics, 2012, 95（6）: 1089-1097.

[7] Nguyen T D and Hong-Hee L. Modulation strategies to reduce common-mode voltage for indirect matrix converters[J]. IEEE Transactions on Industrial Electronics, 2012, 59（1）:129-140.

[8] Shi Dan, Gao You-gang, and Shen Yuan-mao. Harmful electromagnetic effect on affected line from disturbing line[C].Asia-Pacific Conference on Environmental Electromagnetics,Yangzhou, China, 2006: 714-719.

[9] Paul C R. Solution of the transmission-line equations under the weak-coupling assumption[J]. IEEE Transactions on Electromagnetic Compatibility, 2002, 44（3）: 413-423.

[10] 石丹, 高攸纲, 沈远茂. 主扰回路对失配被扰回路的耦合效应[J]. 电波科学学报, 2007, 22（1）: 134-137.Shi Dan, Gao You-gang, and Shen Yuan-mao. Coupling effect between disturbing line and mismatching affected line[J]. Chinese Journal of Radio Science, 2007, 22（1）:134-137.

[11] Cherry P C. FDTD analysis of high frequency electronic interconnection effects[J]. IEEE Transactions on Microwave Theory and Technique, 1995, 43（10）: 2445-2451.

[12] Xie X, Sun D, and Fan R, et al.. Spice simulation and experimental study of transmission line with TVSs excited by EMP[J]. Journal of Electromagnetic Waves and Application,2010, 24（2/3）: 401-411.

[13] Paul C R. Analysis of crosstalk and field coupling to lossy MTL’s in a spice environment[J]. IEEE Transactions on Electromagnetic Compatibility, 1996, 38（3）: 221-229.

[14] 田方, 龚中麟. 混合方法模拟差模传输线的共模电磁泄漏[J].电子与信息学报, 2005, 27（12）: 2001-2004.Tian Fang and Gong Zhong-lin. Simulating the common mode electromagnetic leakage of differential mode cable by a hybrid method[J]. Journal of Electronics & Information Technology, 2005, 27（12）: 2001-2004.

[15] Taflove A, Umashankar K R, Beker B, et al.. Detailed FDTD analysis of electromagnetic fields penetrating narrow slots and lapped joints in thick conducting screens[J]. IEEE Transactions on Antennas Propagation, 1988, 36（2）:247-257.

[16] 方哲, 郁滨, 岳云天. 串行传输线同步信号辐射发射模型研究[J]. 仪器仪表学报, 2013, 34（10）: 2373-2380.Fang Zhe, Yu Bin, and Yue Yun-tian. Study on electromagnetic radiation emission model of serial transmission line synchronization signal[J]. Chinese Journal of Scientific Instrument, 2013, 34（10）: 2373-2380.