认知无线网中一种基于博弈论的低复杂度联合资源共享机制

窦彦智 王满喜 白 铂* 陈 巍 曹志刚

1 引言

认知无线电（Cognitive Radio, CR）技术旨在允许次级用户（Secondary User, SU）监测当前频谱环境，在避免对授权用户（Primary User, PU）造成有害干扰的情况下利用空闲频谱来传输信息，以达到大幅提高频谱利用率，增加无线通信系统容量的目的。美国联邦通信委员会（Federal Communications Commission, FCC）研究了美国境内的频谱利用情况，发现已经注册的频谱并没有被充分利用，提出将CR定位为未来通信的发展方向[1]。

基于认知无线电的频谱共享主要探讨SU与PU之间、SU之间协同接入可用信道的方式。采用的主要理论工具和研究方法包括图论和竞价拍卖理论[2,3]。功率控制则在经典注水功率分配算法的基础上，采用博弈论方法来优化 SU的发射功率，避免对PU通信造成有害干扰[4,5]。然而，目前已有的认知无线网模型大多只包含一个 PU，如文献[2]。同时，部分研究还规定每个频谱子带至多能被一个SU占用，如文献[2,3]。文献[4,5]要求每个SU都知道所有PU所受的干扰情况，来完成自身的功率控制过程。而文献[6-11]则分别提出了利用其他不同的无线网络模型进行动态频谱分配的方法。与前述研究成果不同，本文针对多次级用户和多主用户并存的典型认知无线网络场景，研究动态频谱共享和功率控制问题。本文研究的认知无线网络模型包含多个PU，且允许每个频谱子带被多个基于虚拟多天线技术的SU占用。这样通过提供给SU更多的选择性来进一步增加 SU的收益。针对该网络模型，本文采用博弈论方法联合优化次级用户的发射功率和子带分配，以及主用户的定价系数，以同时最大化主用户和次级用户的收益。

本文的结构如下：第2节提出认知无线网络模型；第3节建立资源共享博弈模型，并将博弈均衡问题的求解分解为3个子优化问题；第4节通过博弈分析，求解每一个子问题，并提出博弈均衡的求解算法；第5节通过仿真验证所提出的理论；第6节是本文的结论。

2 认知无线网络模型

考虑图1所示的认知无线网络，其中，J个PU记为 P1,P2,… ,PJ; K个次级用户对记为 （S1, D1）,（S2,D2）,… ,（SK, DK）。PU的授权频带分为M个子带。在任何时刻，每个 SU只被允许使用至多一个子带。假设子带分配仅在 SU网络里决定，对 PU不可见。

图1 典型认知无线网络模型，其中 L 1 ={S 1 , S 2}

lSk表示分配给 Sk的子带， 并且 lSk∈{1,2,…,M }。那么，每种子带分配策略可表示为向量 lS= [lS1lS2…lSK]。如图1所示，模型允许不同的SU接入同一个子带，并用 Lm表示共享子带m的SU集合，即 Lm={Sk:lSk= m , k = 1 ,2,… , K }。 Lm为空集表示没有 SU选择子带m。信道增益矩阵记为H。

ωSk表示 Sk的发射功率，K个 SU的发射功率可表示为向量 ωS= [ ωS1ωS2…ωSK]。 QP表示PU的干扰容限矩阵，即 QP=[QP1QP2… QPJ]，则每个PU所受的干扰强度要小于其干扰容限，即

其中，“≤”对向量中的每个元素成立。

3 资源共享博弈模型

3.1 博弈行为的时序

在认知无线电中，PU对频带有优先使用权和出租定价权。SU只能根据PU提出的定价系数选择最优频带和最佳发射功率。本文的研究目标是同时最大化PU和SU的收益函数，故PU可视为博弈的领导者（Leader），而 SU 则为跟随者（Follower）。下面给出各参与者博弈行为的时序：

（1）PU同时选择定价系数βj，得到定价系数向量 β= [ β1β2… βJ]。

（2）在SU网络中确定子带分配 lSk，得到子带分配矩阵 lS=[lS1lS2… lSK]。

（3）SU决定其发射功率ωSk，得到发射功率矩阵ωS= [ ωS1ωS2… ωSK]。

根据文献[12]的结论，该博弈模型是一种动态完全信息博弈。

3.2 SU的收益函数

SU的收益kSπ等于收入kR减去支出kC，即

其中， Rk为SU租用某条子带时获得的信道容量，Ck为SU支付给所有PU的租金之和。这里给每个PU的租金等于该PU的定价系数乘以该PU所受到来自各个SU的干扰，即

其中H·k表示H矩阵的第k列。式（3）中的收入和支出都乘以系数1转化成价格，以统一量纲。考虑Lm个 SU共享子带m的情况。假设在子带m, SU网络中发射端距离较近，故可视为Lm-输入Lm-输出的等效虚拟多输入多输出（Multiple-Input and Multiple-Output, MIMO）信道。根据文献[13]的结论，子带m上等效虚拟MIMO信道的容量为

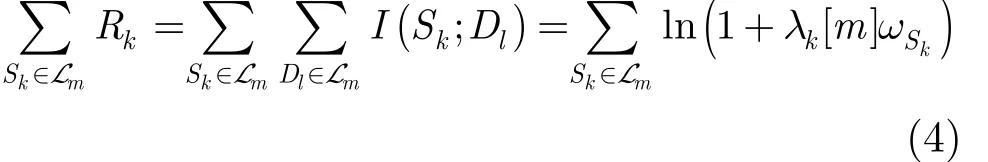
其中， I （ Sk; Dl） 表示子带m中 Sk和 Dl的互信息，λk[m]是中第k个非零特征值，而 G { Sk∈Lm} 是SU网络中满足 Sk∈Lm的收发端信道增益矩阵G的子阵。

基于比例公平原则（Proportional Fairness Criterion, PFC），本文将 Lm集合的总收入分配给每一个SU。根据文献[14]的结论，如果收入分配满足PFC，则合作博弈的纳什议价解可保证整个系统达到帕累托最优。

定理1 如果采用 PFC将 Lm集合总收入分配给每个SU，则每个SU的速率为

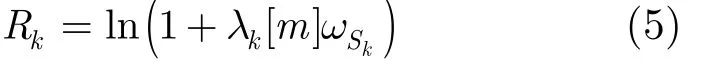
相应收益为

3.3 PU的收益函数

每个PU的收益等于从所有SU收取的租金和，即

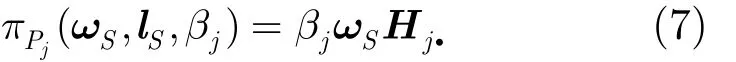
其中，j·H表示H矩阵的第j行。

3.4 均衡的定义

本文已说明前述博弈模型属于动态完全信息博弈，下面要求解该博弈模型的子博弈精炼纳什均衡。根据文献[12]，本文有如下定义：

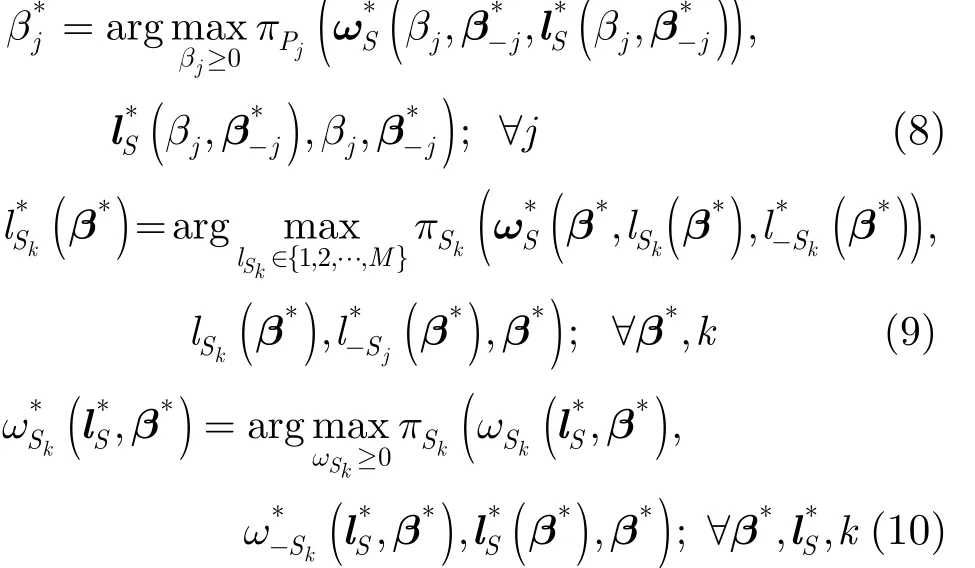
则 （ β*,）构成子博弈精炼纳什均衡。其中,分别代表在给定 βj, lSk（β*）,ω （l*, β*）时的纳什均衡。SkS

3.5 逆向归纳法分解博弈模型

按照逆向归纳法[12]，本文提出的博弈模型可以分解为3个子优化问题。

（1）功率控制问题：PU定价系数 β*、次级网络子带分配已知且固定。对 Sk求满足纳什均衡的发射功率的问题，可表示成式（11）所示的优化问题

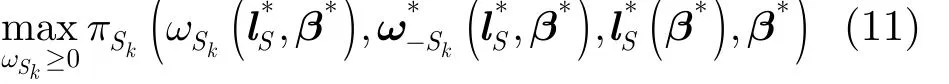
（2）子带分配问题： PU 定价系数 β*已知且固定，通过上一个功率控制问题可求最优发射功率。对 S求满足纳什均衡的子带选择的问题，k可表示成式（12）所示的优化问题：

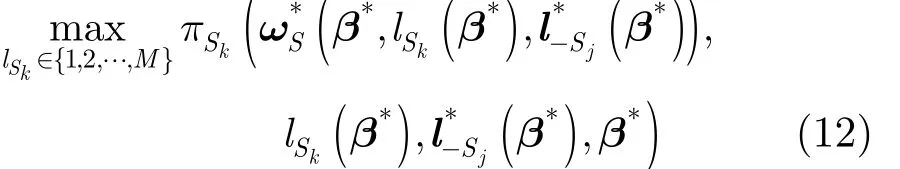
（3）价格调整问题： 通过之前功率控制问题和子带分配问题可求得最优发射功率和最优子带分配。对 Pj求满足功率约束式（1）和纳什均衡的定价系数的问题，可表示成式（13）所示的优化问题

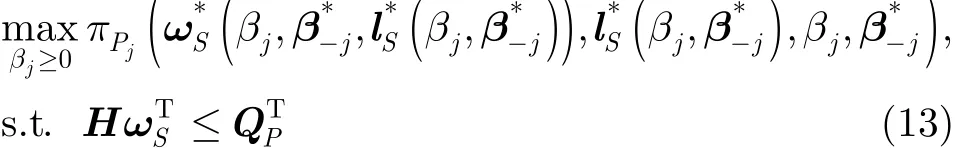
4 资源共享博弈分析

4.1 最优功率控制

对πSk求极大值点，且发射功率要大于0，得

把式（14）代入到式（6），得最大收益表达式为

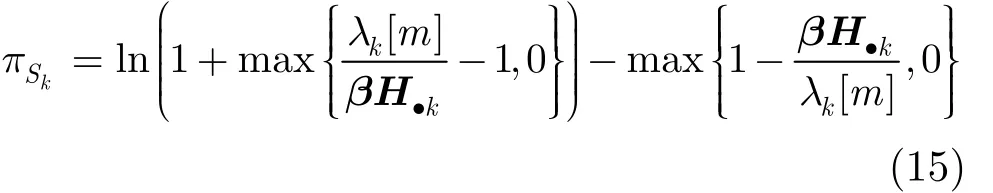
4.2 子带分配算法

在SU从一个子带跳转到另外一个子带的过程中，需要考虑的参数有 λk[m]和hjk[m]。所以很难找到一个非穷举搜索的算法求解纳什均衡。本文则通过记录已经比较过的结果来减少将来的比较次数。

下面给出一个搜索子带分配博弈纳什均衡的算法流程。该算法分为两个步骤，（1）计算所有子带分配情况下每个SU的收益。对于M个子带，K个SU，一共有K

M 种子带分配方式。（2）比较响应情况，如果某种子带分配下所有 SU收益都高于“邻近”情况，则可以判断其为纳什均衡。“邻近”的定义是保持其他 1K- 个SU所选子带不变，仅改变剩下的一个SU的占用子带，共有 1M- 种情况。

4.3 最优定价系数

定理2 如果PU选择β=αc，其中c是一个常矩阵，α是一个正实数，那么 SU最优子带分配是独立于α的。

该定理表明如果定价系数jβ以一个固定速率增大或者减小，那么子带分配博弈的纳什均衡是固定的，这样就可以把子带分配问题从博弈模型中分离出来。

5 仿真验证

本节给出仿真结果，验证前述理论推导和所提算法。考虑2个PU，2个子带，2个SU的情形。可知子带分配一共有4种策略，分别为： S1和 S2共用子带1，记为 { lS1= 1 , lS2= 1 }; S1占用子带2,S2占用子带1，记为 {lS1= 2 , lS2= 1 }; S1占用子带1, S2占用子带 2，记为 { lS1= 1 , lS2= 2 }; S1和 S2共用子带 2，记为 { lS1= 2 , lS2= 2 }。把这4种策略分别标记为策略 1，策略 2，策略3，策略 4。

固定c，改变α，求解纳什均衡策略，得到图2。可以看到，在 α ∈ [ 1,10]，策略 2一直都是纯战略纳什均衡，验证了定理2。在α=4点之后，策略4也成为纳什均衡策略。

图2 固定c，改变α时的纳什均衡

通过改变定价系数组合 c =（c1, c2），研究不同定价系数对于子带分配的影响。如图3，c1从0取到4，c2从0取到2, 2维平面被分成了3部分。灰色区域代表策略2是纳什均衡的，黑色部分表示策略4是纳什均衡的。白色区域表示因为定价太高，两个SU都负担不起租用子带的费用，所以没有纳什均衡。

现在考虑2个PU, 2个子带，5个SU的情形。令α从1取到200, c分别等于 c1和 c2，图4给出了活跃用户数量的曲线图。这里活跃用户定义为发射功率大于0的SU。可以看出，随着α的增加，活跃用户数量越来越少。但是对于不同的定价系数组合c，变化的情况是不同的。

图5给出 α和c对PU所受干扰的影响。从图中可以看出，α越高，则 PU所受干扰越小，所以PU可以通过修改定价系数来实现功率控制。

6 结束语

本文研究了多PU、多SU、多可用子带的认知无线网络中的频谱分配和功率控制问题。首先构建认知无线网络的博弈模型，该模型将 SU网络等效为虚拟 MIMO信道，并采用比例公平原则分配收益，从而允许不同的 SU通过共享子带的方式收发数据。通过给出PU和SU的行为时序，证明了该模型是一种动态完全信息博弈，同时定义了该博弈的子博弈精炼纳什均衡。随后，基于逆向归纳法将上述博弈模型分解成3个子优化问题，并逐一求解。在此基础上，提出了一种搜索纯战略纳什均衡的算法。理论分析证明了PU定价系数满足固定的线性关系时，子带分配结果稳定不变，即子带分配问题可独立求解。因此，本文的理论分析和所提算法为未来认知无线网络的设计提供了理论基础。

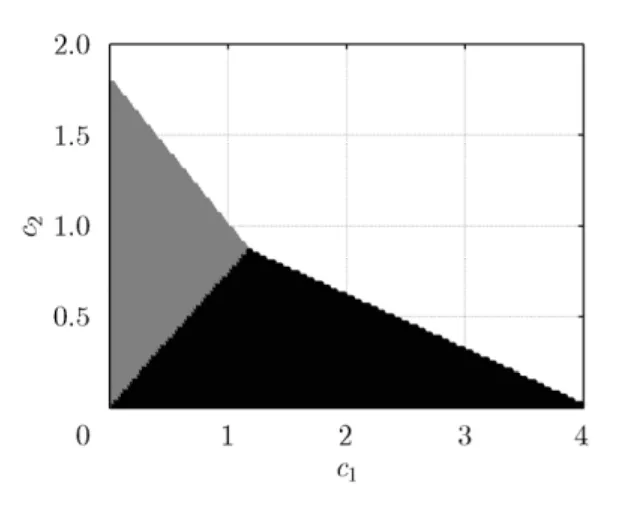
图3 不同的定价系数组合对子带分配的影响

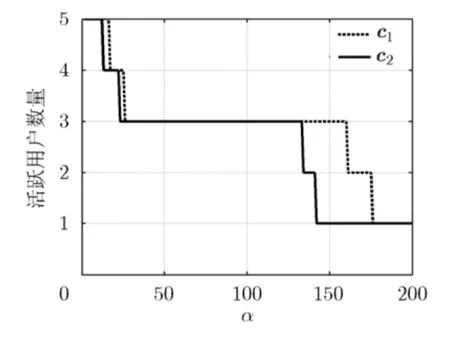
图4 α和c对活跃用户数量的影响

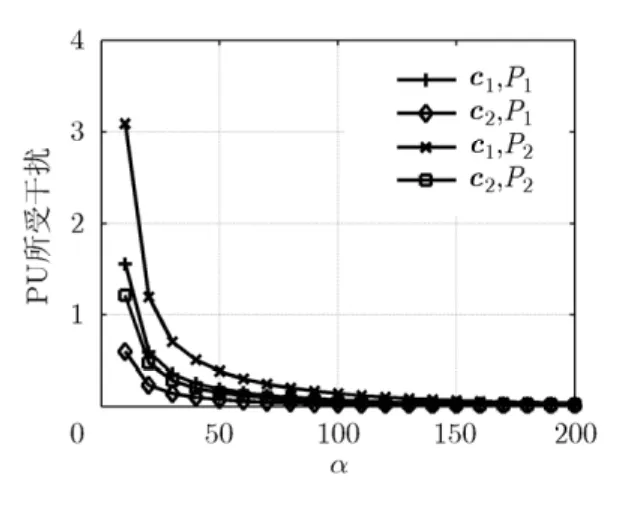
图5 α和c对PU所受干扰的影响

[1] Federal Communications Commission. Spectrum policy task force report[R]. United States: FCC, 2002.

[2] Xiao Y, Bi G, and Niyato D. Distributed optimization for cognitive radio networks using Stackelberg game[C].Proceedings of IEEE International Conference on Communication Systems （ICCS）, Singapore, 2010: 77-81.

[3] Xiao Y, Bi G, and Niyato D. A simple distributed power control algorithm for cognitive radio networks[J]. IEEE Transactions on Wireless Communications, 2011, 10（11）:3594-3600.

[4] Ghasemi A and Sousa E S. Fundamental limits of spectrum-sharing in fading environments[J]. IEEE Transactions on Wireless Communications, 2007, 6（2）:649-658.

[5] Hou Y T, Shi Y, and Sherali H D. Spectrum sharing for multi-hop networking with cognitive radios[J]. IEEE Journal on Selected Areas in Communications, 2008, 26（1）: 146-155.

[6] Ni Q, Zhu R, Wu Z, et al.. Spectrum allocation based on game theory in cognitive radio networks[J]. Journal of Networks, 2013, 8（3）: 712-722.

[7] Lam A, Li V O K, and Yu J J Q. Power-controlled cognitive radio spectrum allocation with chemical reaction optimization[J]. IEEE Transactions on Wireless Communications, 2013, 12（7）: 3180-3190.

[8] Zhang Z, Long K, and Wang J. Self-organization paradigms and optimization approaches for cognitive radio technologies:a survey[J]. IEEE Wireless Communications, 2013, 20（2）:36-42.

[9] Gardellin V, Das S K, and Lenzini L. Self-coexistence in cellular cognitive radio networks based on the IEEE 802.22 standard[J]. IEEE Wireless Communications, 2013, 20（2）:52-59.

[10] Tachwali Y, Lo B F, Akyildiz I F, et al.. Multiuser resource allocation optimization using bandwidth-power product in cognitive radio networks[J]. IEEE Journal on Selected Areas in Communications, 2013, 31（3）: 451-463.

[11] Treeumnuk D, Macdonald S L, and Popescu D C. Optimizing performance of cooperative sensing for increased spectrum utilization in dynamic cognitive radio systems[C].Proceedings of the IEEE International Conference on Communications （ICC）, Budapest, Hungary, 2013:4656-4660.

[12] Robert G. A Primer in Game Theory[M]. 1st Edition, London:FT Prentice Hall Publisher, 1992: 122-129.

[13] Telatar E. Capacity of multi antenna Gaussian channels[J].European Transactions on Telecommunications, 1999, 10（6）:585-595.

[14] Kelly F P, Maulloo A K, and Tan D K H. Rate control for communication networks: shadow prices, proportional fairness and stability[J]. Journal of the Operational Research Society, 1998, 49（3）: 237-252.

[15] Debreu G. A social equilibrium existence theorem[J].Proceedings of the National Academy of Sciences of the United States of America, 1952, 38（10）: 886.