医用直线加速器主要部件对X射线能谱的影响

韩俊杰 朱金汉 张白霖 陈立新 刘小伟

1（中山大学 物理科学与工程技术学院 广州 510275）

2（中山大学 肿瘤防治中心 华南肿瘤学国家重点实验室 广州 510060）

医用直线加速器主要部件对X射线能谱的影响

韩俊杰1朱金汉2张白霖1陈立新2刘小伟1

1（中山大学 物理科学与工程技术学院 广州 510275）

2（中山大学 肿瘤防治中心 华南肿瘤学国家重点实验室 广州 510060）

研究了医用直线加速器的主要部件对X射线能谱的影响。利用蒙特卡罗软件包EGSnrc/BEAMnrc针对Varian600C医用直线加速器，模拟完整及分别去除初级准直器、均整器和次级准直器条件下的相空间文件，通过相空间文件分析程序Beamdp对相空间文件进行分析，分别得到相应条件下的X射线能谱。均整器对能谱的影响非常大，对比于无均整器的情况，有均整器时，平均能量上升了48.9%；但初级准直器、次级准直器对能谱的影响小，平均能量的变化小于1%。在射野内，对比于无均整器的情况，有均整器时，能量注量降低了52.4%，但其空间分布变均匀，非平坦度从15.09%变为1.82%；对比于无初级准直器的情况，有初级准直器时，能量注量上升了1.58%；而对比于无次级准直器的情况，有次级准直器时，能量注量下降了2.00%。均整器对X射线的能谱的影响起主要作用，它能够使X射线的平均能量上升和射野内能量注量的分布变均匀。初级准直器对X射线能谱影响小但对X射线的散射不可忽略，而次级准直器对X射线能谱的影响小而且对X射线的散射作用可以忽略，这些结果对加速器X射线束流模型的建立有一定的参考意义。

初级准直器，均整器，次级准直器，X射线能谱

医用直线加速器是目前放射治疗的主流设备，它用于放射治疗，其原理是利用高能电子打靶产生的韧致X射线对病灶区进行照射，从而达到抑制和控制肿瘤的目的[1]。对医用直线加速器X射线能谱的了解，是建立加速器束流模型和计算吸收剂量的基础。影响医用直线加速器X射线能谱的主要部件包括初级准直器、均整器、次级准直器等。研究医用直线加速器主要部件对X射线能谱的影响，对束流模型的建立及简化将提供有价值的数据，同时对医用直线加速器的设计及优化也有重要的参考价值。对医用直线加速器X射线能谱的研究，主要采用蒙特卡罗方法[2–4]，如Mohan等[3]利用EGS3模拟计算了Varian不同机型的X射线能谱，Ding[2]利用EGS4模拟计算了Varian2100EX的X射线能谱。然而，通过对去除某个主要部件的加速器进行模拟，能更清楚地了解此部件对X射线能谱的影响。随着调强放射治疗的发展，国外两大医用直线加速器厂商Varian以及Elekta均分别推出可无均整(Flattening Filter Free, FFF)的医用直线加速器True Beam及Versa HD。无均整器的医用直线加速器的剂量学特性研究已有相关报道[5–12]。研究去除均整器医用加速器的X射线能谱，对无均整器医用加速器束流模型的建立有很好参考价值。

本文利用蒙特卡罗软件包EGSnrc[13]/BEAMnrc[14]针对Varian600C医用直线加速器，模拟完整及分别去除初级准直器、均整器、次级准直器条件下的相空间文件，通过相空间文件分析程序Beamdp[15]对相空间文件进行分析，得到相应条件下的X射线能谱，从而研究了初级准直器、均整器、次级准直器对X射线能谱的影响，并对医用直线加速器束流模型的建立进行了一些相关的探讨。

1 模型的建立和模拟参数的设置

模拟的医用直线加速器机型是Varian600C，模型示意图如图1所示。模型部件包括靶、初级准直器、均整器、监测电离室、灯光野镜、次级准直器，具体参数由厂家提供。采用EGSnrc结合BEAMnrc

模拟计算了以下4种情况的相空间文件：(1) 包括所有部件的完整模型(Complete model, CM)；(2) 去除初级准直器模型(Lack of primary collimator model, LPCM)；(3) 去除均整器模型(Lack of flattening filter model, LFFM)；(4) 去除次级准直器模型(Lack ofsecondary collimator model, LSCM)。模拟时，通过BEAMnrc的SLABS描述靶；CONS3R描述初级准直器；FlATFILT描述均整器；CHAMBER描述监测电离室；MIRROR描述灯光野镜；JAWS描述次级准直器。模拟的条件为：电子的截止能量ECUT=0.7MeV，光子的截止能量PCUT=0.01MeV；入射电子束的能量设为5.8MeV，其空间分布是半高宽为0.1cm的高斯分布[16]；模拟的初始粒子数为2×107个。为提高模拟效率，采用的减方差技巧为：轫致辐射方向分裂(Directional bremsstrahlung splitting, DBS)，分裂数(NBRsPL)为1 000，分裂野半径FS=10 cm；全局电子射程截断能量Esave设置为2.0 MeV，钨靶的电子射程截断能量Esave设置为0.7MeV。相空间文件的记录平面位于靶下100cm处，记录平面按正方形划分为N个区域，每个的间隔为d，具体划分如图2所示。

图1 加速器模型示意图Fig.1 Sketch map of linear accelerator.

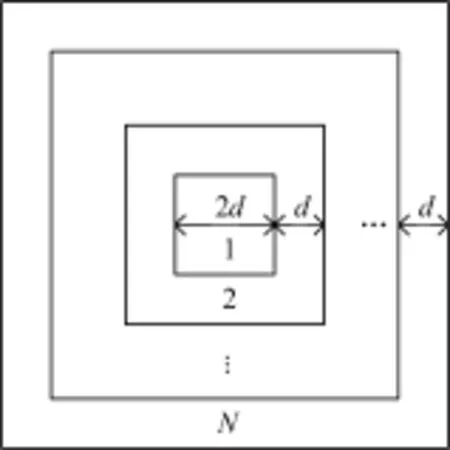
图2 记录平面空间划分示意图Fig.2 Sketch map of recorded plane.

采用Beamdp对模拟得到的相空间文件进行分析。分析时，将能量均匀划分为j个区间，由此得到第i个空间区域X射线的注量φij及第i个空间区域的平均能量Ei、注量φi、能量注量φi。它们之间的关系如下：

式中，ΔE=0.125MeV为能量区间的间隔。

为描述能量注量射野内的均匀性，引入参数非平坦度F，其定义为：

式中，φmax为射野内能量注量的最大值；φmin为射野内能量注量的最小值。

2 结果及分析

2.1 加速器完整模型的X射线能谱及平均能量

图3给出了加速器完整模型模拟得到的i=1、3、5三个空间区域的X射线能谱。模拟的射野为10cm×10cm，划分空间区域的正方形的间隔d=1cm。图3中的能谱图对面积进行了归一，纵坐标表示一个光子在各能量区间所占的份额。为清晰起见，不以直方图的形式表示，而是取能量区间的中点值以及其所对应的注量值连成的曲线来表示。每一个能量区间所对应的注量值的模拟误差大部分都在1%之内。

从图3看出，各空间区域的能谱随着能量的增加发生的变化趋势一致，均是先增大，达到峰值后逐渐减小。但随着离轴距离(Off axis distance)的增加，能谱的峰值逐渐增大，此处离轴距离指的是离射野中心轴的距离。相对区域1，区域3的峰值上升2.28%，而区域5的峰值则上升6.02%；峰值对应的能量则分别在0.875–1MeV和0.75–0.875MeV以及0.75–0.875MeV这三个能量区间内。而且随着离轴距离的增加，低能光子所占的比例逐渐增多。能量小于或等于1MeV的光子注量所占的比例，在区域1为25.1%，区域3为26.3%，区域5为28.2%。图4给出了不同空间区域内的平均能量的离轴变化曲线。从图4中可以看出，随着离轴距离的增加，平均能量逐渐降低，最大的降幅为3.53%。

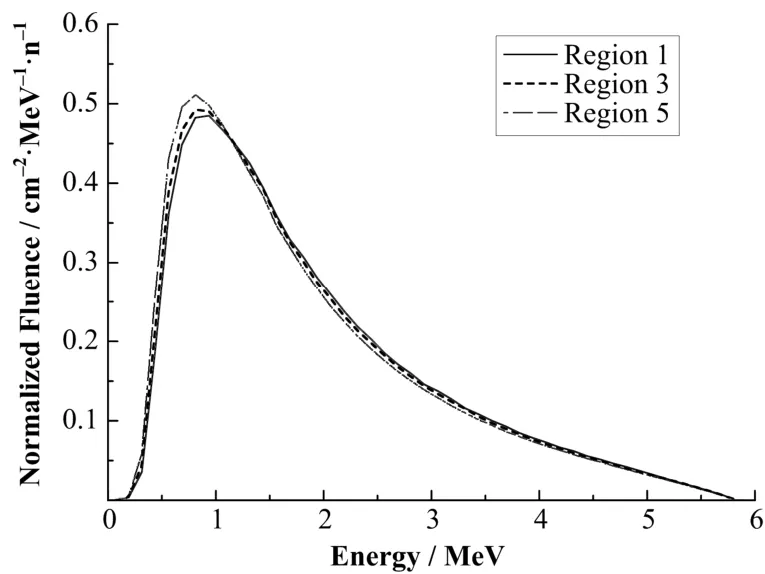
图3 完整模型在不同空间区域的X射线能谱（归一后）Fig.3 Normalized energy spectra of complete model in different regions.

图4 完整模型在射野内的平均能量离轴变化曲线Fig.4 Mean energy profiles of complete model in the radiation field.

2.2 初级准直器、均整器及次级准直器对X射线能谱的影响

由于初级准直器、均整器、次级准直器对射野内不同空间区域能谱的影响规律相同，在此只讨论区域1能谱。模拟的结果表明，均整器对低能光子的吸收明显，有均整器时，能谱峰值从0.25–0.375MeV这一能量区间内右移至0.875–1.0MeV这一能量区间内，能量小于或等于1MeV的光子注量所占的比例，由原来的56.3%降至25.1%。由于完整模型、去除初级准直器模型及去除次级准直器模型的能谱几乎重叠，图5只给出完整模型及去除均整器模型在区域1内的能谱，图中能谱图已经对面积进行了归一。

图6给出了完整模型及去除均整器模型的平均能量离轴变化曲线。相对于无均整器的情况，由于均整器对低能光子的吸收截面较大，均整器使得平均能量增高约50%。在射野内，随离轴距离的增大，完整模型及去除均整器模型的平均能量均下降。对于完整模型，最大的降幅为3.78%，去除均整器模型的最大降幅为0.76%。在射野外，离轴距离5–8cm处，完整模型的平均能量平缓变化；而去除均整器之后，由于缺少来自均整器的散射光子，因此去除均整器模型的平均能量逐渐上升。而完整模型、去除初级准直器及去除次级准直器模型在射野内X射线的平均能量的差异小于1%。

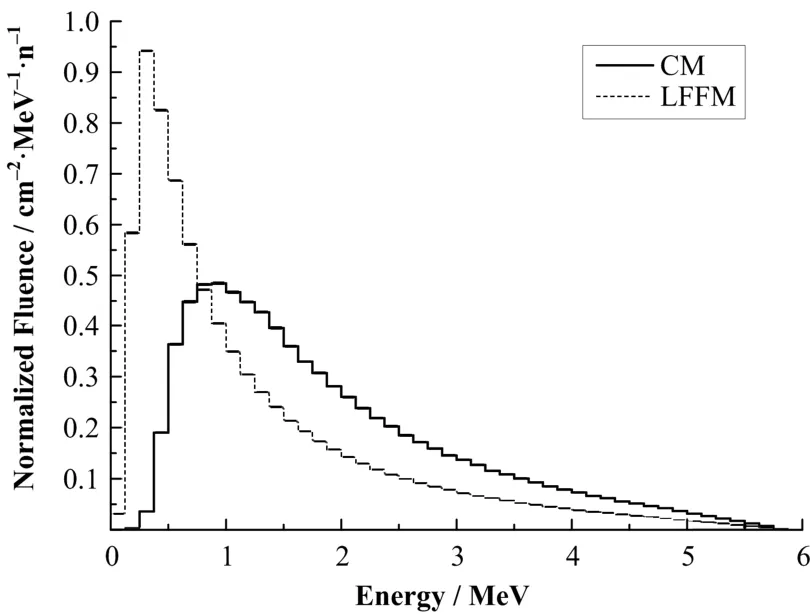
图5 相同区域内不同模型的能谱（归一后）的比较Fig.5 Normalized energy spectra of different models in the same region.

图6 有无均整器的平均能量离轴变化曲线Fig.6 Mean energy profiles with and without flattening filter model.

2.3 初级准直器、均整器及次级准直器对X射线能量注量的影响

图7给出了完整模型、去除初级准直器模型、去除次级准直模型的能量注量离轴变化曲线。由图7给出的结果对比可知，有初级准直器时射野内的能量注量上升，平均上升幅度为1.58%，射野内最大的上升幅度为2.80%，这主要是由于初级准直器对X射线的散射造成的；而由于次级准直器对X射线的吸收，有次级准直器时射野内的能量注量下降，平均下降幅度为2.00%，射野内最大的下降幅度为3.02%。

图8给出了完整模型及去除均整器模型的X射线能量注量离轴变化曲线。由图8可知，相对于无均整器的情况，有均整器时能量注量下降明显，最大的下降幅度为56.4%，射野内平均下降幅度约为52.4%；有均整器时，射野内能量注量变得均匀，非平坦度F从无均整器时的15.09%下降到1.82%。

图7 不同模型的能量注量离轴变化曲线Fig.7 Energy fluence profiles for different models.

2.4 射野内总能量注量和平均能量

表1给出了10cm×10cm的射野内完整模型及去除初级准直器、去除均整器、去除次级准直器的加速器模型的X射线能量注量、平均能量。由表1可知，初级准直器使得光子注量上升1.58%，平均能量下降0.25%；均整器使得光子能量注量下降52.5%，平均能量上升48.9%；次级准直器使得光子能量注量下降2.00%，平均能量上升0.75%。

表1 射野内各不同情况的光子能量注量、平均能量Table 1 Photon energy flux, mean energies in the radiation field for different models.

3 讨论

X射线束流模型的建立应该包含原射线和散射线。原射线是指电子打靶发生韧致辐射产生的光子，此光子不与机头部件发生互相作用而直接到达记录平面。通常对原射线建模时[17]，把原射线假设成点源；散射线是指从靶产生的韧致辐射光子与机头的部件发生一次或者多次相互作用之后的光子，其中散射线最大的来源是均整器，其次是初级准直器。

从模拟结果上看，初级准直器使得10cm×10cm的射野内光子注量上升1.83%，能量注量上升1.58%。这说明初级准直器对X射线有散射作用，在建立加速器束流模型时需加以考虑。

由于初级准直器对X射线有散射作用，对散射源建模时，如果只采用一个散射源，可通过设置散射源的尺寸大于均整器的尺寸，将初级准直器与均整器的散射作用同时考虑。而无均整器医用直线加速器的建模时，应该把散射源放置于初级准直器的下表面，宜建成一个环状源[18]。

次级准直器的存在使得射野内光子注量下降2.73%，能量注量下降2.00%，这是因为次级准直器对散射光子的吸收作用引起的。变量ZLAST[15]能对相空间中粒子的Z轴坐标进行统计分析。利用ZLAST对完整模型的相空间文件进行分析可知，来自于次级准直器的光子数只占总光子数的0.2%，因此在进行束流模型建模时，可以不考虑次级准直器对束流的散射，把次级准直器看成吸收体。

4 结语

均整器对X射线能谱的影响起主要作用，它能够使束流的平均能量上升和射野内能量注量的空间分布均匀；初级准直器对X射线能谱影响小但对X射线的散射不可忽略；而次级准直器对X射线能谱的影响小而且对X射线的散射作用可以忽略。这些结果对加速器X射线束流模型的建立有一定的参考意义。

1 殷蔚伯, 陈波, 张春立, 等. 2011 年中国大陆地区第六次放疗人员及设备调查[J]. 中华放射肿瘤学杂志, 2011, 20(6): 453–457. DOI: 10.3760/cma.j.issn.1004-4221.2011. 003

YIN Weibo, CHEN Bo, ZHANG Chunli, et al. The six nationwide survey on radiation oncology of continent prefecture of China in 2011[J]. China Radiation Oncology, 2011, 20(6): 453–457. DOI: 10.3760/cma.j.issn.1004-4221.2011.003

2 Ding G X. Energy spectra, angular spread, fluence profiles and dose distributions of 6 and 18 MV photon beams: results of Monte Carlo simulations for a Varian 2100EX accelerator[J]. Physics in Medicine and Biology, 2002, 47(7): 1025–1046. DOI: 10.1088/0031-9155/47/ 7/303

3 Mohan R, Chui C, Lidofsky L. Energy and angular distributions of photons from medicallinacs[J]. Medical Physics, 1985, 12(5): 592–597

4 Baumgartner A, Steurer A, Josef M F. Simulation of photon energy spectra from Varian 2100C and 2300C/D linacs: simplified estimates with PENELOPE Monte Carlo models[J]. Applied Radiation and Isotopes, 2009, 67(11): 2007–2012

5 Cashmore J. The characterization of unflattened photon beams from a 6 MV linac[J]. Physics in Medicine and Biology, 2008, 53(7): 1933–1946. DOI:10.1088/ 0031-9155/53/7/009

6 Vassiliev O N, Titt U, Pönisch F, et al. Dosimetric properties of photon beams from a flattening filter free clinical accelerator[J]. Physics in Medicine and Biology, 2006, 51(7): 1907–1917. DOI: 10.1088/0031-9155/51/ 7/019

7 Almberg S S, Frengen J, Lindmo T. Monte Carlo study of in-field and out-of-field dose distributions from a linac operating with and without a flattening-filter[J]. Medical Physics, 2012, 39(8): 5194–5203. DOI: 10.1118/ 1.4738963

8 Kragl G, afWetterstedt S, Knäusl B, et al. Dosimetric characteristics of 6 and 10 MV unflattened photon beams[J]. Radiotherapy and Oncology, 2009, 93(1): 141–146. DOI: 10.1016/j.radonc.2009.06.008

9 Mesbahi A. Dosimetric characteristics of unflattened 6 MV photon beams of a clinical linac: a Monte Carlo study[J]. Applied Radiation and Isotopes, 2007, 65(9): 1029–1036. DOI: 10.1016/j.apradiso.2007.04.023

10 Zavgorodni S. Monte Carlo investigation into feasibility and dosimetry of flat flattening filter free beams[J]. Physics in Medicine and Biology, 2013, 58(21): 7699–7713. DOI: 10.1088/0031-9155/58/21/7699

11 Dzierma Y, Licht N, Nuesken F, et al. Beam properties and stability of a flattening-filter free 7 MV beam–an overview[J]. Medical Physics, 2012, 39(5): 2595–2602. DOI: 10.1118/1.3703835

12 陈勇, 张旭光, 倪婕, 等. 西门子直线加速器均整和未均整射束的光子束剂量学特性[J]. 核技术, 2012, 35(3): 179–184

CHEN Yong, ZHANG Xuguang, NI Jie, et al. Photon beam dosimetric characteristics of SIEMENS linac with/without flattening filter[J]. Nuclear Techniques, 2012, 35(3): 179–184

13 Kawrakow I, Mainegra-Hing E, Rogers D. The EGSnrc code system: Monte Carlo simulation of electron and photon transport[R]. NRCC Report PIRS-701, National Research Council, Otawa, Canada, 2010

14 Rogers D W O, Walters B, Kawrakow I. BEAMnrc user’s manual[R]. NRC Report PIRS, 2001: 509

15 Ma C M, Rogers D W O. BEAMDP user’s manual[J]. NRC Report PIRS, 2010: 509

16 陈少文, 王学涛, 陈立新, 等. 医用直线加速器的Monte Carlo 模拟[J]. 核电子学与探测技术, 2009, 29(2): 328–331

CHEN Shaowen, WANG Xuetao, CHEN Lixin, et al. Monte Carlo simulation for medical linac[J]. Nuclear Electronics and Detection Technology, 2009, 29(2): 328–331

17 Tillikainen L, Siljamäki S, Helminen H, et al. Determination of parameters for a multiple-source model of megavoltage photon beams using optimization methods[J]. Physics in Medicine and Biology, 2007, 52(5): 1441–1467. DOI: 10.1088/0031-9155/52/5/015

18 Wong Cho, Kayla Kielar, Ed Mok, et al. Multisource modeling of flattening filter free (FFF) beam and the optimization of model parameters[J]. Medical Physics, 2011, 38(4): 1931–1942. DOI: 10.1118/1.3560426

CLC TL53

Effects of main components of clinical linac on X-ray energy spectra

HAN Junjie1ZHU Jinhan2ZHANG Bailin1CHEN Lixin2LIU Xiaowei1
1(School of Physics and Engineering, Sun Yat-sen University, Guangzhou 510275, China)
2(State Key Laboratory of Oncology in South China, Cancer Center of Sun Yat-sen University, Guangzhou 510060, China)

Background: It is well known that the main components of clinical linac such as the primary collimator, flattening filter and secondary collimator affect the X-ray energy spectra. How does it appear is the foundation of dose calculation, and it is helpful for building up a beam model. Purpose: This paper aims to make a detailed study on the effects of these main components on the X-ray energy spectra of a clinical linac beam. Methods: Monte Carlo program EGSnrc/BEAMnrc is employed to build up the beam model of Varian 600C linac, as well as the other three different beam models: without primary collimator, without flattening filter, without secondary collimator at the same time. After respective simulations, we use Beamdp program to analyze the phase space files, so as to obtain energy spectra for different models. Results: Flattening filter has heavy influence on X-ray beam’s energy spectra, the mean energy increases by 48.9% compared with its absence. But the primary collimator and secondary collimator have little influence on energy spectra, the change of mean energy is within 1% compared their absence. In the center field size of 10 cm×10 cm, flattening filter could let the energy fluence decrease by 52.4%, but the distribution becomes more flat and the unflatness changes from 15.09% to 1.82%; primary collimator could increase energy fluence by 1.58%; but secondary collimator could decrease the energy fluence by 2.00%. Conclusion: Flattening filter has mainly influence on the energy spectra of X-ray beam, it could let the mean energy increase and the energy fluence distribution become more flat; the scatter of primary collimator for X-ray beam must be taken into account whilst the scatter of secondary collimator for X-ray beam can be neglected. The results are meaningful to build a X-ray beam model for clinical linac.

Primary collimator, Flattening filter, Secondary collimator, X-ray energy spectrum

TL53

10.11889/j.0253-3219.2015.hjs.38.100202

广东省产学研研究项目(No.2012B091000144)资助

韩俊杰，男，1991年出生，2013年毕业于中山大学，现为硕士研究生，专业为粒子物理与原子核物理

刘小伟，E-mail: stslxw@mail.sysu.edu.cn

2015-04-27，

2015-09-27