钻井液侵入对储层电阻率影响的数值模拟与实验研究
2015-12-13王敏李万才冯雪唐志远刘国昌
王敏,李万才,冯雪,唐志远,刘国昌
(1.中国石化东北油气分公司勘探开发研究院,吉林 长春130062;2.空军航空大学基础基地基础部数学教研室,吉林 长春130000;3.中海油能源发展工程技术研究院,天津300457;4.中国石油大学(北京)地球物理与信息工程学院,北京102249)
0 引 言
钻井过程中,在泥浆滤液侵入影响下,利用电阻率测井方法不能直接测量地层真电阻率。泥浆侵入地层与泥浆滤液性质、地层物理性质以及浸泡时间有关,难以精确获得钻井泥浆侵入程度和深度对储层电阻率的影响。阶跃模型是研究泥浆侵入过程的传统方法[1],该模型假设地层可动烃被钻井液按照活塞方式完全驱替,侵入带具有均匀的含水饱和度和电阻率,且侵入带和原状地层之间存在明显的界限,即发生跃变。钻井过程中,钻井液侵入储层过程非常复杂,饱和度、电阻率等地层参数在侵入过程中的变化并非像阶跃模型所描述的那样发生突变,而是一个渐变的过程[2]。张建华等[3]模拟计算了钻井液侵入对储层电阻率的影响,但模拟过程采用的孔隙度为常数,由于钻井液侵入过程中,泥浆颗粒进入孔隙和喉道,引起储层孔隙度值降低,因此模拟钻井液侵入时孔隙度和渗透率在时间和空间上应该是变量。马明学等[4]针对泥浆微粒的堵塞问题提出了一种数学模型,但是模拟结果并没有得到实验证实。迄今为止,钻井液侵入机理研究多数基于数值模拟和小岩样驱替实验,没有得到全直径实体模型的验证。因此,进行钻井全过程钻井液侵入岩心模拟实验研究尤为重要。
本文采用数值模拟和物理模拟相结合的办法进行研究。数值模拟方面,根据钻井液侵入机理,利用多孔介质的两相渗流方程,建立泥浆侵入渗透性地层的数学模型,计算不同地层条件下侵入剖面上流体参数径向分布特征;物理模拟方面,采用多功能全直径长岩心测试系统,测试泥浆侵入岩心引起的电阻率随时间变化特征。通过数值模拟和实验测试相结合,评价钻井液的侵入过程,储层流体的移动情况,为求解地层物性参数、确定地层饱和度、电阻率的分布等测井解释技术提供理论依据。
1 泥浆侵入机理及物理模拟
钻井过程中,当泥浆矿化度低于或者高于地层水矿化度时,油气层与水层径向侵入剖面的电性特征将发生变化,泥浆矿化度与地层水矿化度的差距越大,油气层与水层径向侵入剖面的电性特征越明显。泥浆柱与地层间的压差使泥浆渗入地层,径向上形成冲洗带、过渡带和原状地层带,造成井筒附近地层的电性特征和流体性质发生变化,使储层的测井响应趋于复杂。无论是识别油气层还是水层,或是定性分析原状地层电阻率及确定饱和度参数等,都需要考虑泥浆滤液侵入油气层对测井响应的影响。
为模拟实际情况,采用的物理模拟实验装置原理图见图1。该测试系统为中国石油西部钻探工程有限公司测井公司测井新技术研究中心研制,已被证实可以在不同温度、压力、钻井液侵入条件下进行岩心模拟实验研究[5]。该测试系统包括MCD-C型多功能岩心实验装置、模拟泥浆动滤失发生器和流量计装置。通过对沿岩心轴向方向上选取多个样点,测量泥浆侵入前后岩心电阻率和渗透率的变化,评价其损害程度,得到泥浆侵入深度与损害程度的关系。
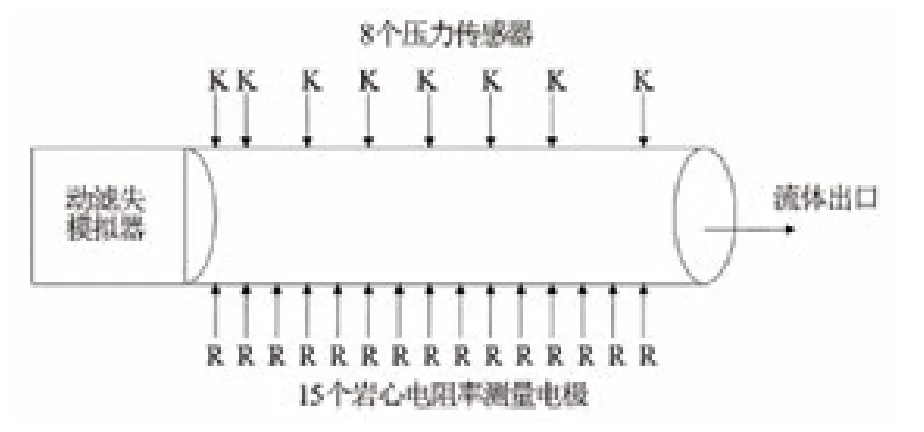
图1 泥浆侵入电阻率测试实验装置示意图
该设备基本实验参数:围压2~50MPa,温度20~150℃,岩心直径4.5cm,长度3~142cm,渗透率测量范围0.5~1000mD*非法定计量单位,1mD=0.987×10-3μm2,下同。沿岩心轴向方向上可定点测试8个测点的渗透率值和15个测点的电阻率值。实验过程中温度和围压为常温常压,分析钻井液侵入前后岩心电性物性的相对变化。利用钻井液侵入压差模拟钻井压差,模拟地层压力系数为1.1,正压差为6~7MPa。钻井液体系配方:原浆+2.2%PSC+2.1%磺化沥青+1.8%FSP+1%CMC+2%SPNh+2%超细碳酸钙+10.3%单向压力封闭剂,采用的模拟油为普通煤油。
实验步骤:① 将实验所用的岩心加工、烘干、饱和、称重,测得原始孔隙度(侵入前孔隙度);② 用所配地层水正向测量岩心的原始渗透率和岩心原始电阻率;③ 钻井液侵入动、静滤失实验;④ 用②所配的地层水正向测量岩心的侵入后渗透率,钻井液侵入后,用来确定损害深度和程度;⑤ 将岩心烘干称重测得侵入后的孔隙度。
为分析岩心在不同孔隙度和渗透率条件下,钻井液侵入对岩心的污染,分别将不同孔隙度和渗透率的岩心在相同条件下进行钻井液侵入实验,考察在钻井液侵入前后岩心孔隙度的变化特征。图2是不同岩心在侵入10h后岩心各点孔隙度值。通过实验可以看出,侵入后岩心孔隙度明显降低,靠近驱替端部分降低最严重,远离驱替端的岩心孔隙度受到损害比较小;微粒侵入对高孔隙度高渗透率岩心的污染更严重。
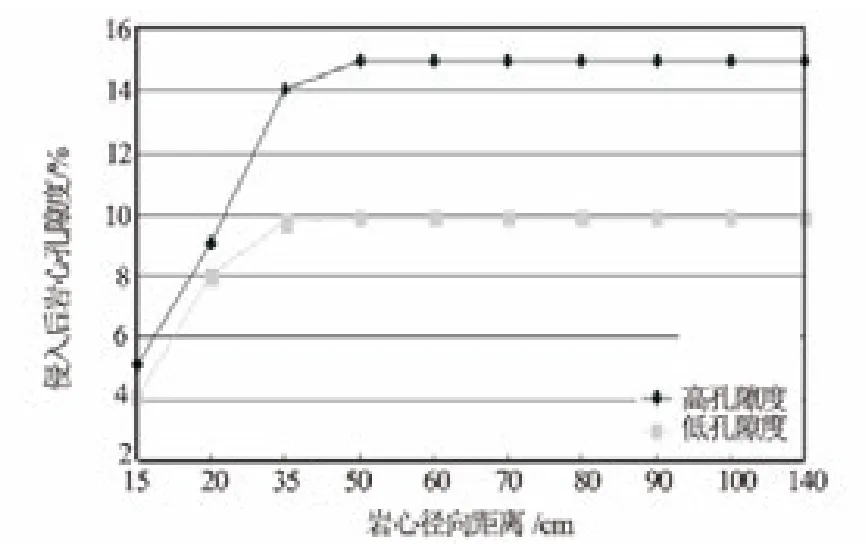
图2 泥浆侵入后孔隙度的变化
2 泥浆侵入的数值模拟
2.1 油水两相渗流方程
在油田注水开发保持压力开采的过程中,如无游离气析出,原油饱和压力将基本保持原始饱和度压力的数值,此时可以假设饱和压力为常数,不用考虑饱和压力变化对原油性质的影响。石济民等[6]和邓少贵等[7]建立的达西渗流模型就是基于该基本假设。对二维两相渗流问题
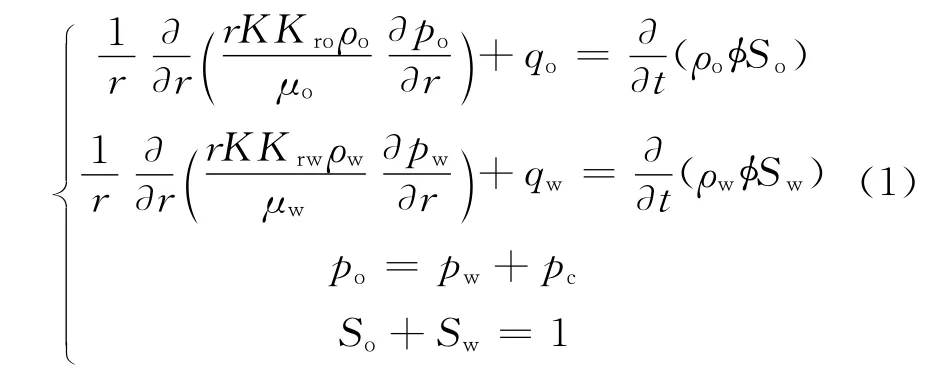
式中,qo=0,qw=0,qo、qw分别为油、水产量;po、pw分别为油相、水相压力;μo、μw分别为油、水黏度;So、Sw分别为含油、含水饱和度;φ为地层孔隙度;K、Kro、Krw分别为地层绝对渗透率、油相和水相相对渗透率;r为地层径向半径;t为侵入时间。
方程组(1)考虑了岩性、流体、重力以及相对渗透率的影响,还考虑了储层非均质性的影响。方程的未知变量的函数包括密度、相对渗透率、毛细管压力、孔隙度,因此为非线性方程。为了简化计算过程,忽略重力、毛细管力以及饱和度方程中水弹性性质的影响,得到压力方程和饱和度方程
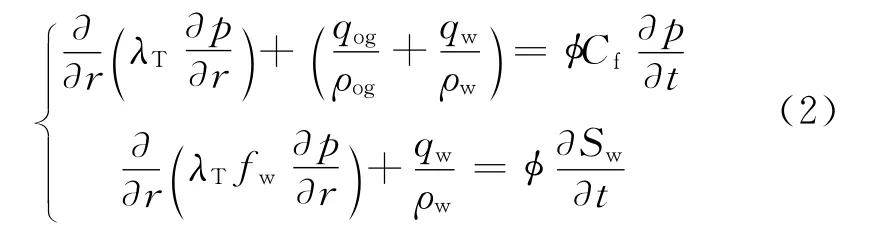
为了推导方便,暂时略去产量项,在x-y平面坐标系展开,有
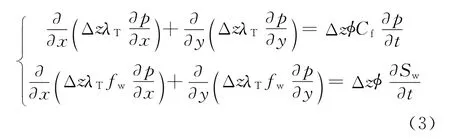
式中,λT=K(Krw/μw+Kro/μo);fw=Krw/(Krw+μwKro/μo);Cf为 孔 隙 压 缩 系 数,Cf=φoCR/φ+SwCw+(1-Sw)Co。
对方程组(3)采用五点隐式差分格式求解,把引起非线性的系数做显式处理,得到
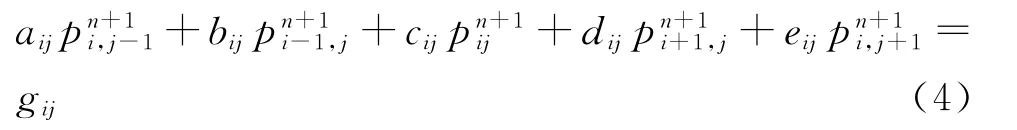
求出压力pn+1后,代入饱和度方程显式求解。国外一些公司软件采用的是压力和饱和度交错求解的方法。由于解压力方程是隐式求解,当网格节点数很多时,求解方程费时但稳定性好,时间步长可以适当取大一些;饱和度方程是显式求解,计算速度快但稳定性差,时间步长应取小一些。压力方程不变,其时间步长为Δtp。求得pn+1后,将 Δtp分为m小段,每段为Δts。这样,每求一步压力,可求m次饱和度,mΔts=Δtp,这就是一步压力多步饱和度方法。根据方程组中的饱和度方程,可得
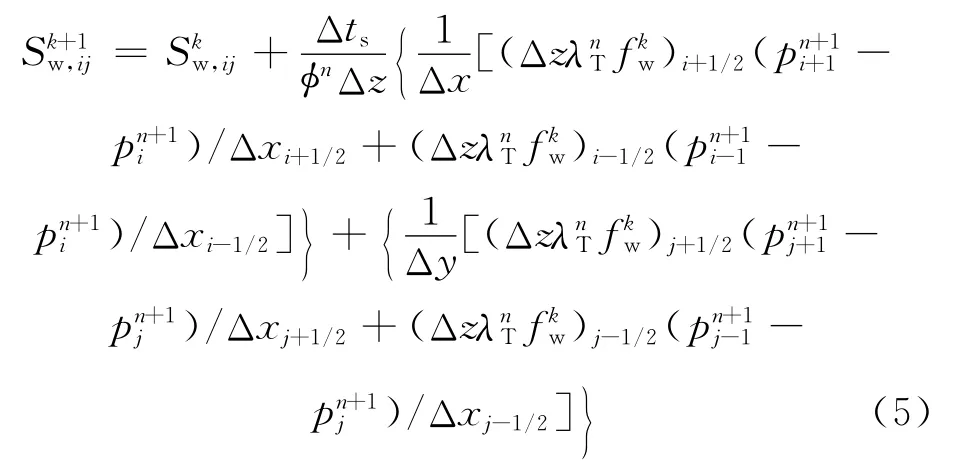
2.2 钻井液侵入参数设置
井壁泥饼的形成及其渗透性对钻井液侵入有重要影响。泥饼的形成过程非常复杂,与储层孔渗条件、泥浆性能、泥浆柱压力、钻井环境等多种因素有关,真实模拟泥饼形成过程比较困难。Tobola等[8]研究表明,泥饼渗透率随时间推移呈指数下降,并且远小于地层渗透率,是控制钻井液侵入地层的主要因素。本文参考Zhang等[9]的经验公式计算泥饼渗透率Kmc为式中,Kmco为泥饼初始渗透率,这里取值为岩心渗透率。
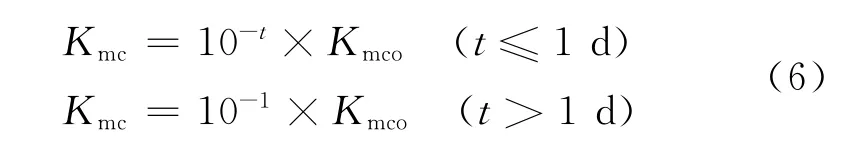
钻井液矿化度Cmf一般和地层水的矿化度不同,它们之间的物理混合满足扩散方程[10]
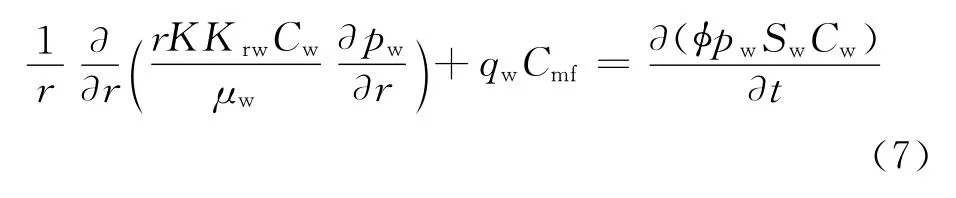
式中,Cw表示水的矿化度。
式(2)和式(7)分别代表钻井液侵入储层的驱替和混合过程。数值模型求解首先是由油水两相渗流方程(2)分别求出岩心各点的压力和含水饱和度信息,然后代入扩散方程(6)求出岩心各点的矿化度。利用式(7)求出各点的地层水电阻率,最后把各个参数代入Archie公式(8)得出岩心各点的电阻率[11]。
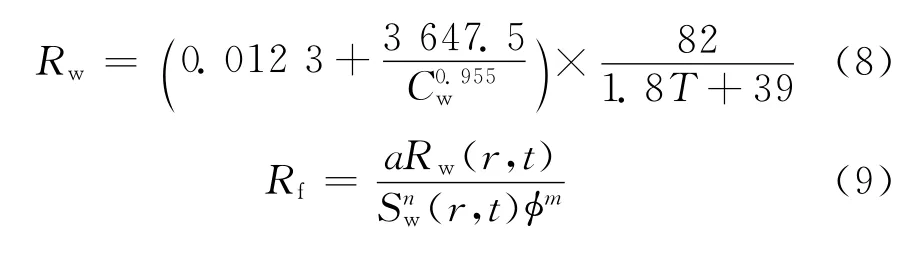
式中,T为地层温度;a为常数;m为胶结指数;n为饱和度指数;本文中取值a=1,m=n=1.78。
3 模拟结果分析
3.1 数值模拟结果
基于上述模型,对钻井液侵入进行数值模拟。模拟所需基本输入参数包括原始岩心压力p、驱替压力pw、原始水饱和度Sw、原始岩心含水矿化度Cw、温度T、岩心孔隙度φ、渗透率K、钻井液密度ρmf以及Kro、Krw—Sw和pc—Sw关系等。根据实验数据,岩心模拟参数中孔隙度和渗透率随时间变化。
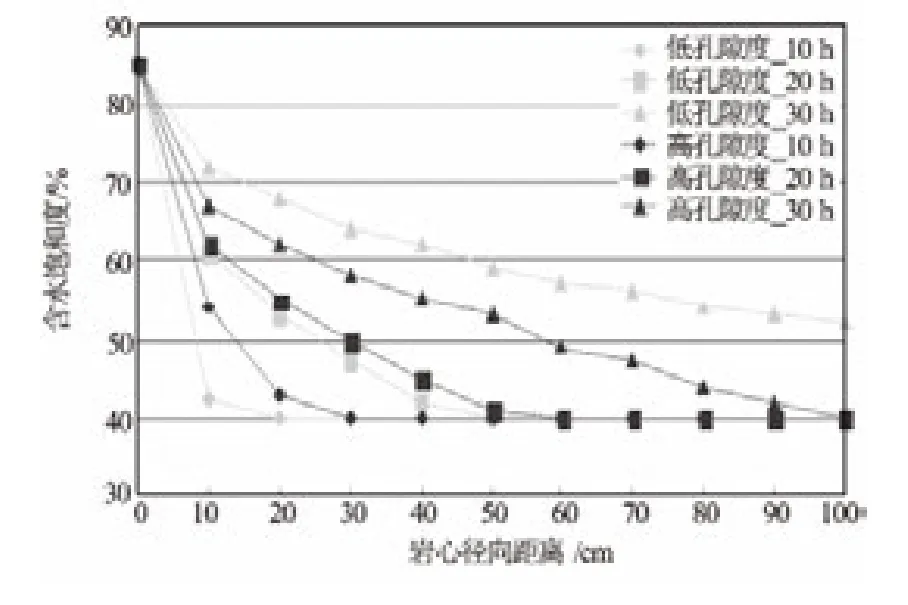
图3 岩心各点饱和度随时间的变化
图3为分别模拟低孔隙度(10%)和高孔隙度(20%)情况下,不同时间岩心各点的含水饱和度分布。可以看出,① 井眼附近的区域含水饱和度最高,受到污染最严重,表明在钻井开始,泥浆侵入非常快,该区域可以认为是冲洗带,而中间过渡带处在驱替和混合扩散过程,含水饱和度是一个渐变的过程;②10h以内高孔隙度储层侵入距离比低孔隙度要远,这是因为大孔隙度情况下,泥浆滤液更容易渗入储层;③ 长时间条件下高孔隙度储层侵入的距离要比低孔隙度储层浅,这是因为泥浆颗粒大量侵入高孔隙度储层,在井壁和靠近井眼的储层很快形成内、外泥饼,减缓了泥浆滤液的侵入,而且大孔隙度需要更多的泥浆滤液填充。
图4是模拟初始含水饱和度分别为50%、35%、20%,在侵入时间为10h的条件下岩心各点电阻变化率的变化。可以看出,初始含水饱和度越高,钻井液侵入越深。这是因为,储层含水率增加,使得驱替中所需要更多的泥浆滤液来替换原来储层孔隙中的流体,使得钻井液侵入速度减小。
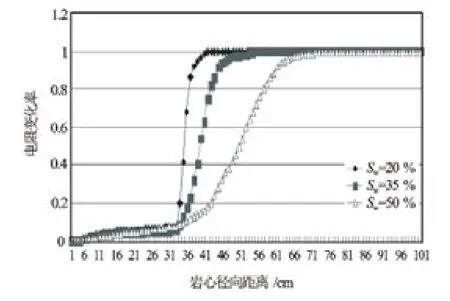
图4 不同初始含水饱和度对电阻变化率影响
图5为模拟岩心各点电阻变化率随着时间变化的图版,可以看出,① 岩心各点电性参数并不是均匀的沿径向分布,也不像阶跃模型所描述的那样在冲洗带、过渡带和原状地层之间发生跃变,而是有一个渐变的过程;② 侵入初期,高孔隙度储层受到侵入影响比较大,但是由于泥浆微粒大量侵入,以及泥饼的快速形成,在长时间的条件下,低孔隙度储层受到污染要比高孔隙度储层严重;③ 钻井液侵入对储层电阻率影响与时间有关。
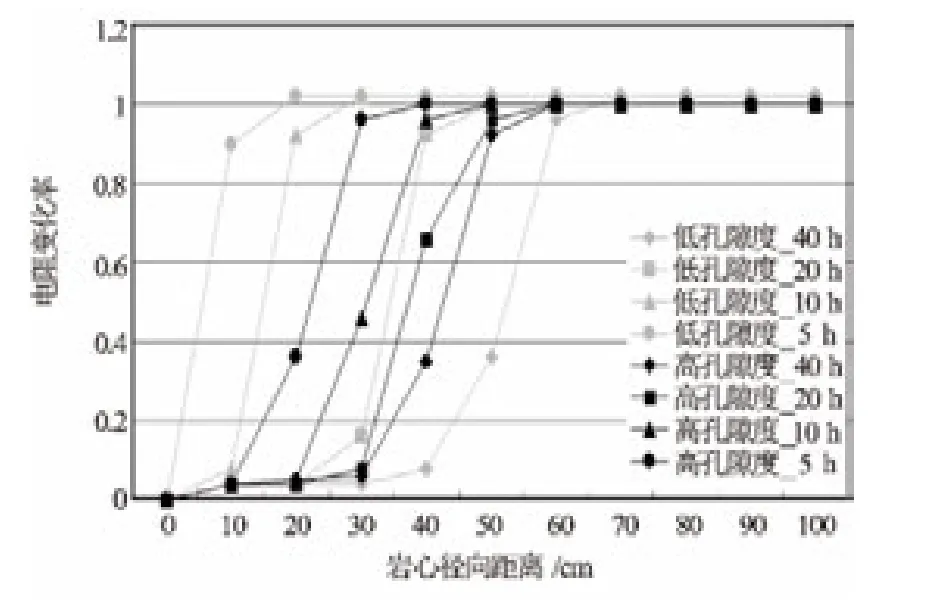
图5 不同时间岩心各点电阻的变化率
3.2 数值模拟和实验结果对比
图6为实验测量得到的各点电阻率随时间的变化。实验所用岩样是中等孔隙度中等渗透率(孔隙度15.6%,渗透率100mD),饱和地层水Cw=200g/L,钻井液矿化度Cmf=20g/L。图7为数值模拟结果,模拟采用的参数与实验一致。图6与图7中r代表岩心从左到右的各个节点。
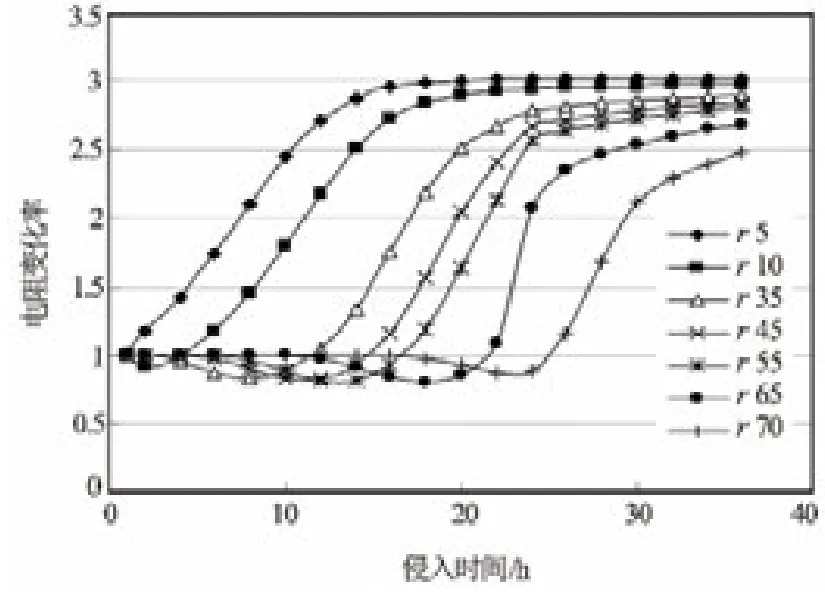
图6 各点电阻变化率随时间的变化(实验结果)
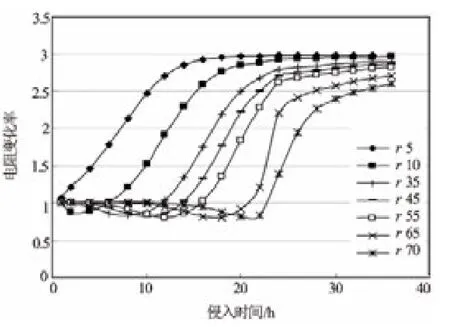
图7 各点电阻变化率随时间的变化(数值模拟结果)
图6与图7的对比分析可以看出,① 模拟结果与实验结果一致性较好;② 岩心左端(驱替端)电阻先开始变化,而且比较早地处于平衡状态;③ 岩心右端的节点在侵入一段时间后电阻才开始变化,而且平衡所用时间很长。因此证实,钻井液侵入后储层冲洗带、过渡带、原状地层的电阻率不是突变,而是渐变的过程,并且与钻井液性质、地层物性、侵入时间有关。
4 结 论
(1)钻井过程中,钻井液会不同程度侵入含油气储层,引起井筒周围地层流体饱和度和电阻率发生变化,在泥饼、侵入带的多重影响下,电阻率测井难以反映原状地层真实情况。
(2)储层孔隙度渗透性与钻井液侵入深度关系表明:高孔隙度高渗透率储层由于泥浆固相颗粒大量侵入,通过表面沉淀、孔喉堵塞、孔隙充填的方式迅速在井壁和靠近井眼储层中形成泥饼,因泥饼渗透率远小于储层,因此侵入距离较浅;而低孔隙度储层因孔隙比较小,形成泥饼比较慢,侵入会一直进行。长时间条件下,低孔隙度储层的侵入距离更远,污染更严重。
(3)储层初始含水饱和度越高,侵入速度越快,相同时间内侵入越深。
(4)经物理模拟实验证实,基于多孔介质两相渗流模型、不同矿化度流体对流传递模型和阿尔奇公式建立的数学模型能较好模拟不同条件下侵入剖面上电性和流体参数的径向分布特征。
[1]Elton H,Darrel C,David Allen.Quantitative Invasion Description[C]∥SPWLA 33rd Annual Logging Symposium,1992,1-20.
[2]魏丹.钻井液侵入机理及储层电阻率测井响应特征应用研究[D].青岛:中国石油大学(华东),2005.
[3]张建华,胡启,刘振华.钻井泥浆滤液侵入储集层的理论计算模型[J].石油学报,1994,15(4):73-78.
[4]马明学,鞠斌山.一种新的计算泥浆侵入储层电阻率分布的数学模型[J].测井技术,2004,28(6):503-507.
[5]袁兆羽,何峰江.砂岩储层钻井液侵入及二次污染测井评价实验研究[C]∥第三届测井技术交流会论文集,2007:18-24.
[6]石济民,林振宝,岳兴业.三维三相黑油模型的MILU-CG方法及数值结果比较[J].石油勘探与开发,1994,21(6):46-52.
[7]邓少贵,杨震,李智强,等.大斜度井/水平井复杂介质双侧向测井响应数值模拟[J].测井技术,2009,33(1):32-36.
[8]Tobola D P,Holditch S A.Determination of Reservoir Permeability from Repeated Induction Logging[J].SPE Formation Evalution,1991:20-26.
[9]Zhang J H,Hu Q,Liu Z H.Estimation of True Formation Resistivity and Water Saturation with a Time Lapse Induction Logging Method[J].The log analyst,1999,40(2):138-148.
[10]林纯增,张舫.钻井液侵入特征的测井应用[J].测井技术,2001,26(4):341-346.
[11]胡国恒,姚永君,等.钻井液侵入对储层电性物性影响实验研究[J].测井技术,1998,23(5):323-326.
