Meshless Local Petrov-Galerkin and RBFs Collocation Methods for Solving 2D Fractional Klein-Kramers Dynamics Equation on Irregular Domains
2015-12-13DehghanAbbaszadehandMohebbi
M.Dehghan,M.Abbaszadeh and A.Mohebbi
Meshless Local Petrov-Galerkin and RBFs Collocation Methods for Solving 2D Fractional Klein-Kramers Dynamics Equation on Irregular Domains
M.Dehghan1,M.Abbaszadeh2and A.Mohebbi3
In thecurrentpaper thetwo-dimensional timefractional Klein-Kramers equation which describes the subdiffusion in the presence of an external force field in phase space has been considered.The numerical solution of fractional Klein-Kramers equation is investigated.The proposed method is based on using finite difference scheme in time variable for obtaining a semi-discrete scheme.Also,to achieve a full discretization scheme,the Kansa’s approach and meshless local Petrov-Galerkin technique are used to approximate the spatial derivatives.The meshless method has already proved successful in solving classic and fractional differential equations as well as for several other engineering and physical problems.The fractional derivative of equation is described in the Riemann-Liouville sense.In this paper we use a finite difference scheme to discretize the time fractional derivative of mentioned equation as the obtained scheme is of convergence order O(τ1+γ)for 0< γ< 1.Also,we solve the mentioned equation on non-rectangular domains.The aim of this paper is to show that the meshless methods based on the strong form i.e.the radial basis functions collocation approach and local weak form i.e.meshless local Petrov-Galerkin idea are also suitable for the treatment of the fractional Klein-Kramers equation.Numerical examples confirm the high accuracy and acceptable results of proposed schemes.
Time fractional Klein-Kramers equation,finite difference schemes,meshlesslocal Petrov-Galerkinapproach(MLPG),Kansamethod,radial basisfunctions(RBFs),Caputo fractional derivative,Riemann-Liouville fractional derivative.
1 Introduction
In recent years there has been a growing interest in the field of fractional calculus[Miller and Ross(1974);Oldham and Spanier(1974a);Podulbny(1999)].Fractional differential equations have attracted increasing attention because they have applications in various fields of science and engineering.Many phenomena in fluid mechanics,viscoelasticity,chemistry,physics,finance and other sciences can be described very successfully by models using mathematical tools from fractional calculus,i.e.,the theory of derivatives and integrals of fractional order.Some of the most applications are given in the book of Oldham and Spanier(1974b),the book of Podulbny(1999)and also,Bagley and Torvik(1983).Many considerable works on the theoretical analysis[Diethelm and Ford(2002);Wess(1996)]have been carried on,but analytic solutions of most fractional differential equations can not be obtained explicitly,so proposing new method to finding the numerical solutions of these equations is of practical importance.There are several definitions of a fractional derivative of order α>0[Oldham and Spanier(1974b,a)].The two most commonly used are the Riemann-Liouville and Caputo.The difference between the two definitions is in the order of evaluation.We start with recalling the essentials of the fractional calculus.The fractional calculus is a name for the theory of integrals and derivatives of arbitrary order,which unifies and generalizes the notions of integer-order differentiation and n-fold integration.The classic Klein-Kramers equation in phase space,as the description of the probability distributionu(x,y,t)of a Brownian particle,with positionxand velocityy,in a fluid,is to the following form[Gao and Sun(2012)]
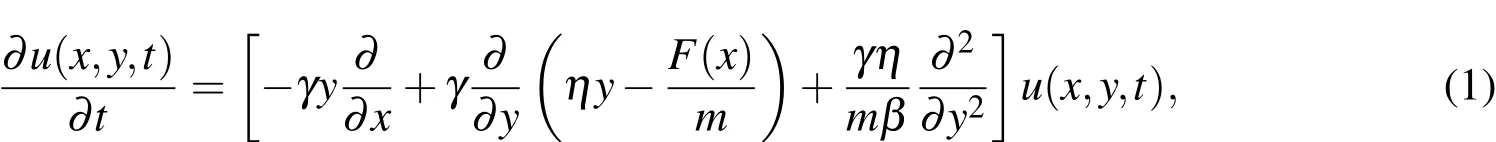
wheremis the mass of the particle,γ is the ratio of the intertrapping time scale and the internal waiting scale,η is the friction constant,with κBthe Boltzmann constant andthe temperature of the surrounding medium,F(x)= Φ′(x)is an external field.As said in Deng(2007),anomalous diffusion is one of the most ubiquitous phenomena in nature,and it appears in a wide variety of physical situations,for instance,transport of fluid in porous media,diffusion of plasma,diffusion at liquid surfaces,etc Deng(2007).Also,as mentioned in Gao and Sun(2012)this model has been widely used in molecular chemical reactions in solvents[Bicout and Berezhkovskii(2001)],dielectric response of dipole molecules[Coffey,Kalmykov,and Titov(2004)],dynamics of cell migration[Dieterich,Klages,Preuss,and Schwab(2008)],biological modeling[Hadeler,Hillen,and Lutscher(2004)],escape problem over a barrier[Kalmykov,Coffey,and Titov(2006)],the droplet condensation,evaporation[Widder and Titulaer(1993)].In the classical theory of Brownian transport the phase space dynamics are described by the deterministic Klein-Kramers equations[Orzeł and Weron(2011)].The Klein-Kramers equation for the first time was introduced by Klein in 1922[Gao and Sun(2012)].Many analytic methods were used for solution of Klein-Kramers equation,but these methods are difficult for application.Therefore,numerical methods need to be involved.As said in Gao and Sun(2012);Selinger and Titulaer(1984),the one-dimensional Klein-Kramers equation is equivalent to the Langevin equation,hence,it can be numerically approximated by solving the stochastic differential equation.Authors of Selinger and Titulaer(1984)have explored a numerical technique for determining the structure of the kinetic boundary layer of the Klein-Kramers equation for noninteracting Brownian particles in a fluid near a wall that absorbs the Brownian particles.In Trahan and Wyatt(2004)the trajectory method and a stationary lattice finite difference algorithm are applied in phase space to solve the classical Klein-Kramers and quantum modified Caldeira-Leggett equations for two examples:a double-well oscillator in contact with a thermal bath and the decay of a metastable state.The kinetics of thermally activated processes are studied in Cartling(1987)by the nonstationary solutions of the Fokker-Planck equation,or Kramers’equation,for a particle moving in a bistable potential and coupled to a heat bath using an alternate direction implicit method.Authors of Chen,Liu,Zhuang,and Anh(2009)proposed some practical numerical methods to solve a class of initial-boundary value problems for the fractional Fokker-Planck equation on a finite domain.Also,Chen,Liu,Zhuang,and Anh(2009)studied the solvability,stability,consistency,and convergence of these methods.
Recently,the fractional Klein-Kramers equation introduced by Metzler and Klafter(2000).Incorporating subdiffusive mechanisms into the Klein-Kramers formula leads to the fractional Klein-Kramers equation[Deng and Li(2011)].Then,the equation can effectively describe subdiffusion in the presence of an external force fi eld in the phase space[Deng and Li(2011)].As said in Gao and Sun(2012),the generalized equation of the Rayleigh and Fokker-Planck types could be deduced from the fractional Klein-Kramers equation.Interested readers can see Bicout and Berezhkovskii(2001);Coffey,Kalmykov,and Titov(2004);Magdziarz and Weron(2007);Metzler and Sokolov(2000).For example,the main aim of Gao and Sun(2012)is to propose a finite difference approach for the fractional Klein-Kramers equation with appropriate initial and boundary conditions,also,convergence and stability of the scheme are analyzed using the energy method.Authors of Li,Deng,and Wu(2012)proposed a numerical procedure for solving the Lévy fractional Klein-Kramers equation using the explicit and implicit finite difference schemes.The main aim of Liu,Anh,and Turner(2004)is to present a finite difference scheme for solving the space fractional Fokker-Planck equation(SFFPE)with instantaneous source.Authors of Deng and Li(2011)have developed the L1-CDIS and GL-CDIS schemes to numerically solve the fractional Klein-Kramers equation,describing the subdiffusion in the presence of the external field in the phase space.The rigorous stability and error analysis are presented,the two schemes have the same stability conditions but different convergent order in time direction.Authors of Orzeł and Weron(2011),using a subordination method,identified a two-dimensional stochastic process(position,velocity)whose probability density function is a solution of the fractional Klein-Kramers equation.Authors of Deng,Chen,and Barkai(2015)discussed the numerical algorithms for the forward and backward fractional Feynman-Kac equations with fractional substantial derivative and they used finite difference methods to solve both the forward and backward fractional Feynmann-Kac equations,and the finite element methods are applied to solve the backward fractional Feynmann-Kac equation.The main aim of Saadatmandi and Dehghan(2010)is to propose a new Legendre operational matrix to the fractional calculus for solving fractional differential equations.Also we refer the interested reader to Cui(2012,2014);Deng(2008)for more research works on the numerical solution of fractional differential equations and to Esmaeili and Shamsi(2011)for fractional differential equations.
1.1 A brief review of the meshless method
In recent years radial basis functions(RBFs)have been extensively used in different context and emerged as a potential alternative in the field of numerical solution of PDEs.The use of RBFs in the numerical solution of partial differential equations(PDEs)has gained popularity in engineering and science community as it is meshless and can readily be extended to multi-dimensional problems.The key idea of the meshless methods is that they can obtain accurate and stable solution of integral equations or partial differential equations with various boundary conditions with a set of particles without using any mesh[Mirzaei and Dehghan(2010)].The most important advantages of meshless methods compared to finite element methods are:their high-order continuous shape functions,simpler incorporation of hand p-adaptivity and certain advantages in crack problems.
A truly meshless method,called the Meshless Local Petrov-Galerkin(MLPG)method was discussed in depth in Atluri(2004).A local symmetric weak form(LSWF)for linear potential problems is developed,and a truly meshless method,based on the LSWF and the moving least squares approximation,is presented for solving potential problems with high accuracy in Atluri and Zhu(1998).Authors of Atluri and Shen(2002)studied the efficiency and accuracy of various meshless trial and test functions based on the general concept of the meshless local Petrov-Galerkin(MLPG)method.Five types of trial functions,and six types of test functions are introduced in Atluri and Shen(2002).Recently,many fractional partial differential equations are solved using meshless approach based on the radial basis functions and moving least squares(MLS)approximation.Authors of Liu,Liu,Turner,Anh,and Gu(2014)considered a fractional differential equation to describe a model of mobile/immobile transport with a power law memory function and solved it using RBFs collocation method on the different domains.Authors of Gu,Zhuang,and Liu(2011)presented an implicit meshless collocation technique for time fractional diffusion equation.Also,the stability and convergence of this meshless technique are investigated theoretically and numerically.Authors of Gu,Zhuang,and Liu(2010)presented an implicit meshless approach based on the radial basis functions for numerical simulation of the anomalous sub-diffusion equation.Also,they discussed on thestability and convergenceof their method.Authors of Liu,Gu,Zhuang,Liu,and Nie(2011)presented an implicit meshless approach based on the radial basis functions for numerical simulation of time fractional diffusion equation.Authors of Zhuang,Liu,Anh,and Turner(2008)presented an implicit meshless approach based on the moving least squares(MLS)approximation for the numerical simulation of fractional advection-diffusion equation.A meshless local Petrov-Galerkin(MLPG)method is applied in Sladek,Sladek,Krivacek,Wen,and Zhang(2007)to solve dynamic plate bending problems described by the Reissner-Mindlin theory.The meshless local Petrov-Galerkin(MLPG)method is used in Sladek,Sladek,and Hon(2006)to solve stationary and transient heat conduction inverse problems in 2-D and 3-D axisymmetric bodies.Authors of Sladek,Sladek,Zhang,and Schanz(2006)employed a meshless method based on the local Petrov-Galerkin approach for the numerical solution of quasistatic and transient dynamic problems in two-dimensional(2D)nonhomogeneous linear viscoelastic media.Authors of Sladek,Stanak,Han,Sladek,and Atluri(2013)proposed a meshless local integral equation(LIE)method for numerical simulation of 2D pattern formation in nonlinear reaction-diffusion systems.The local boundary integral formulation for an elastic body with nonhomogeneous material properties is presented in Sladek,Sladek,and Atluri(2000).Meshless methods based on the local Petrov-Galerkin approach are proposed in Sladek,Sladek,and Atluri(2004a)for solution of steady and transient heat conduction problems in a continuously nonhomogeneous anisotropic medium.The meshless local Petrov-Galerkin method is used in Sladek,Sladek,Hellmich,and Eberhardsteiner(2007)to analyze transient heat conduction in 3-D axisymmetric solids with continuously inhomogeneous and anisotropic material properties.A meshless method based on the local Petrov-Galerkin approach is proposed in Sladek,Sladek,and Atluri(2004b)for solution of static and elastodynamic problems in a homogeneous anisotropic medium.The Heaviside step function is used as the test function in the local weak form.
The approach of meshless method has already proved successful in standard quantum mechanics as well as for solving several other engineering and physical problems[Dehghan and Shokri(2007);Dehghan and Salehi(2011);Shokri and Dehghan(2010a)].Also we refer the interested reader to Abbasbandy,Ghehsareh,and Hashim(2013,2012)for more researches work on meshless method of radial basis functions.
Authors of Dehghan and Shokri(2007)proposed a numerical scheme to solve the two-dimensional Schrödinger equation using collocation points technique based on the multiquadrics(MQ)and the Thin Plate Splines(TPS)radial basis function(RBF).The main aim of Dehghan and Mirzaei(2008)is to employ the meshless local Petrov-Galerkin(MLPG)method for the numerical solution of the twodimensional non-linear Schrödinger equation.Authors of Dehghan and Salehi(2011)combined the boundary knot and the analog equation methods for solving two-dimensional regularized long-wave equation.A meshless collocation method based on the radial basis functions is applied in Dehghan and Tatari(2008)for solving the one-dimensional parabolic partial differential equation subject to given initial and nonlocal boundary conditions.Authors of Dehghan and Shokri(2008)proposed a numerical scheme for solving the two-dimensional damped-undamped sine-Gordon equation in which the presented numerical algorithm is based on the meshless collocation method using the radial basis functions(RBFs)and the thin plate splines(TPS)approximations.The main aim of Dehghan and Salehi(2014)is to develop a meshless local Petrov-Galerkin(MLPG)method based on the shape functions of the moving least squares reproducing kernel(MLSRK)for solving the 2-D time-dependent Maxwell equations.Authors of Taleei and Dehghan(2014)introduced an efficient truly meshless method based on the weak form for interface problems as the proposed method combines the direct meshless local Petrov-Galerkin method with the visibility criterion technique to solve the interface problems.
The aim of the current paper is to show that the meshless methods based on both the strong form and local weak form i.e.RBFs collocation approach and meshless local Petrov-Galerkin technique are also suitable for the treatment of fractional Klein-Kramers equation which describes the subdiffusion in the presence of an external force field in phase space[Magdziarz and Weron(2007);?);Orzeł and Weron(2011)].
1.2 The main aim of this paper
In this paper,we consider the time fractional Klein-Kramers equation to the following form

with boundary conditions

and initial condition

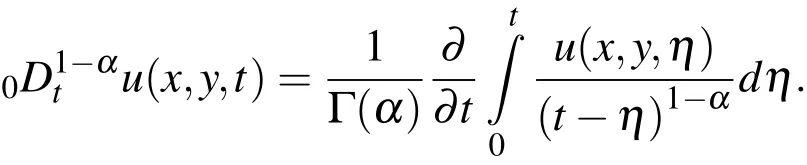
Up to the best of authors’knowledge,there are many partial differential equations with fractional derivative that some of them are obtained by substituting the fractional derivative with the classical derivative[Metzler and Klafter(2000)].But the fractional Klein-Kramers equation is one of the fractional PDEs that is derived with physical justification.The interested readers can find more details in Metzler and Klafter(2000).In the next,we explain some informations taken from Metzler and Klafter(2000)for deriving the fractional Klien-Kramers equation.The following equation is the stochastic differential equation corresponding to the classical Klien-Kramers

As is said in Metzler and Klafter(2000)the Klein-Kramers equation with classical derivative is derived based on the Chapman-Kolmogorov equation for a Markovian process[Metzler and Klafter(2000)]

The transfer kernel in Eq.(6)is thereby given through

in which ψ describes the distribution of transitions with the velocity increment Δvfor the field variablesvandxwhere the position increment is connected with the mean time step Δtthrough Δx=vΔt.The coefficients[Metzler and Klafter(2000)]

can be determined by Eq.(5).By some preliminaries,the transfer kernel splits up into two parts:
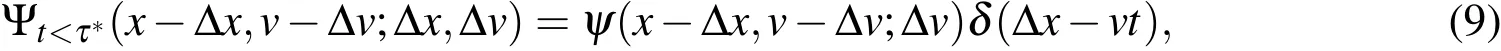
and

Using the special processes by the generalized Chapman-Kolmogorov equation,we have[Metzler and Klafter(2000)]

Now,using the Laplace transformation of Eq.(11)and omitting some small terms,we arrive at the fractional Klien-Kramer equation as follows[Metzler and Klafter(2000)]

The outline of this paper is as follows:
In Section 2,we explain RBFs approximation method.In Section 3,we obtain a semi-discrete scheme with convergence order of O(τ1+γ).The implementation of RBF meshless method for the two-dimensional time fractional Klein-Kramers dynamics equation is given in Section 4.In Section 5,we explain the moving least squares approximation.Also,in this section,we express implementing the meshless local Petrov-Galerkin method for solving the considered model in the current paper.In Section 6,we report the numerical experiments of solving Eq.(2)with the methods developed in this investigation for some test problems and compare the results with those reported in literature.Finally a conclusion is given in Section 4.
2 Preliminary of RBFs approximation method
As mentioned in[Liu and Gu(2005)]the definition of a meshfree method is:
A meshfree method is a method used to establish system algebraic equations for the whole problem domain without the use of a predefi ned mesh for the domain discretization[Liu and Gu(2005)].
Also,as said in[Liu and Gu(2005)]meshfree methods use a set of nodes scattered within the problem domain as well as sets of nodes scattered on the boundaries of the domain to represent(not discretize)the problem domain and its boundaries.These sets of scattered nodes are called field nodes,and they do not form a mesh,meaning it does not require any a priori information on the relationship between the nodes for the interpolation or approximation of the unknown functions of field variables.In this paper,we use the meshfree method based on RBFs collocation approach.The reason we use the RBFs collocation method is that it works for arbitrary geometry with high dimensions and it does not require a mesh at all.The meshfree method using RBFs is the so-called Kansa’s method[Kansa(1990b,a);Kansa,Aldredge,and Ling(2009)],where the RBFs are directly implemented for theapproximation of the solution of PDEs.Kansa’s method was developed in 1990,in which the concept of solving PDEs by using RBFs,especially MQ,was initiated.As mentioned in Vanani and Aminataei(2008),the MQ approximation scheme was fi rst introduced by Hardy[Hardy(1971)]who successfully applied this method for approximating surface and bodies from field data.In this section we introduce the basic definitions of radial basis functions in general case and we express some basic theorems for the interpolation error using radial basis functions.
Definition 1.[Fasshauer(2007);Wendland(2005)]A symmetric function φ∈Rd×Rd−→R is strictly conditionally positive definite of orderm,if for all setsX={x1,...,xN}⊂ Rdof distinct points,and all vectors λ ∈Rdsatisfyingp(xi)=0 for any polynomialpof degree at mostm−1 the quadratic form
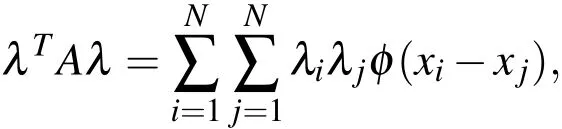
is positive,whenever λ/=0.
We interpolate a continuous functionf:Rd−→R on a setX={x1,...,xN}with choosing the radial basis function for φ :Rd−→ R that is radial in the sense that φ(x)= Ψ(‖x‖),where‖.‖is the usual Euclidean norm on Rdas we will explain in the next section.Now,we assume φ to be strictly conditionally definite of orderm,then the interpolation function has the following form
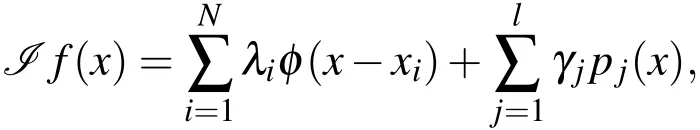
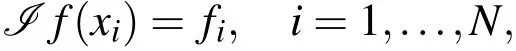
and forlremaining conditions we use the following equations

Some popular choices of RBFs include Shokri and Dehghan(2010b)are listed in the following table where the free parametercis called the shape parameter[Shokri and Dehghan(2012)]of the RBFs.

Name of function Definition Linear r Cubic r3 Multiquadratics(MQ) ■r2+c2 Gaussian(GS) e−cr2 polyharmonic splines r2n ln(r),r2n−1
A mentioned in Rippa(1999)the accuracy of many schemes for interpolating scattered data with radial basis functions depends on a shape parameter,c,of the radial basis function.Author of Rippa(1999)showed,numerically,that the optimal value ofcdepends on the number and distribution of data points,on the data vector,and on the precision of the computation and he presented an algorithm for selecting a good value for c that implicitly takes all the above considerations into account.Also,authors of Huang,Yen,and Cheng(2010)showed,numerically,that RBF in fact performs better than polynomials,as the optimal shape parameter exists not in the limit,but at a finite value.Interested readers can see Ling(2012);Ling and Schaback(2009);Ling and Kansa(2005);Ling,Opfer,and Schaback(2006).
3 Time discretization
In this section,we express a scheme for discretization of Eq.(2).We introduce the following notation
tk=kτ,k=0,1,...,N,
where τ=T/Nis the step size of time variable.We need the following definition and lemma for getting the time-discrete scheme.
Definition 4.[Zhuang and Liu(2009)].Lety(t)∈L1(a,b),the integral
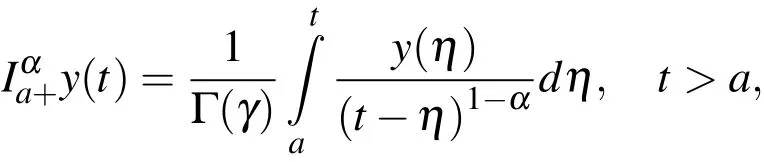
where α > 0,is called the Riemann-Liouville fractional integral of order γ.
Lemma 1.[Zhuang and Liu(2009)].Ify(t)∈C2[0,T],then

in which

Integrating both sides of Eq.(2)on the[tk,tk+1],gives

Applying Lemma 1 and the following relation

we have
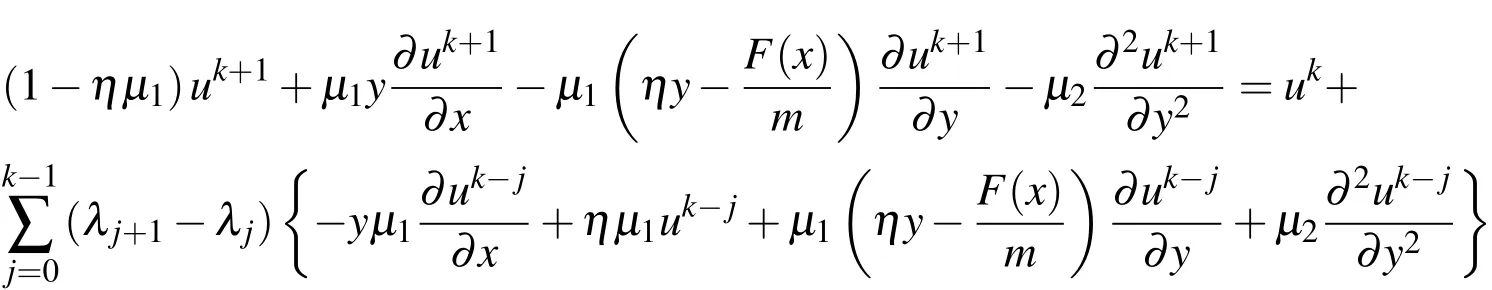
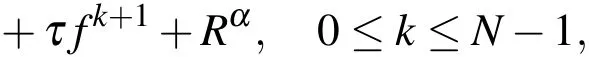
Omitting the small termRα,we can obtain the following relation fork=0,1,2,...,N−1

Eq.(13)is the first time-discrete scheme(FTDS),in which the convergence order in time variable is
4 RBF Meshless Method
We assume that Ω is an arbitrary domain in R2.The approximate expansion ofu(xi,yi,tn)is as follows

in which

For the use of Kansa’s method,we letbeMcollocation points in Ω in whichare boundary points andare interior points.For each point(xi,yi),let us denote
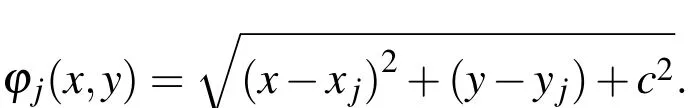
4.1 Full discretization using scheme(13)
In relation(13)fork=0 we get the following form
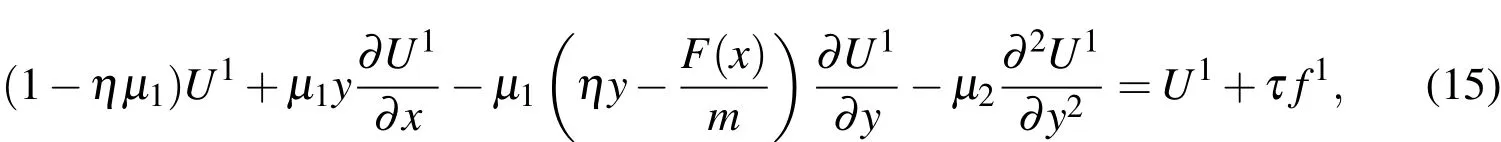
and for 1≤k≤N−1 we have
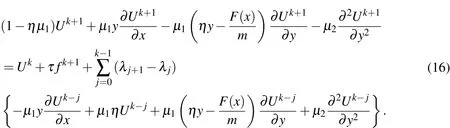
Now substituting(14)into(15)and(16)results the following matrix form

in which

and

in which
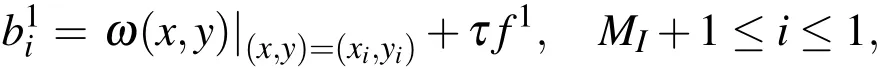
and also


After solving the algebraic system of equations Ack=Bkat each time step,we can construct the solution using(14).The coefficient matrix,A,is ill-conditioned,therefore we use the LU decomposition for solving the algebraic system of equations Ack=Bk.
5 Moving least squares(MLS)shape functions
This subsection is taken from book of Liu and Gu(2005).We consider an unknown scalar function of a field variableu(x)in the domain Ω.The MLS approximation ofu(x)is defined at x as[Liu and Gu(2005)]

where p(x)is the basis function of the spatial coordinates andmis the number of the basis functions.When p(x)=[x,y]Twe usually select the following basis functions[Liu and Gu(2005)]

also this basis function is built using monomials from the Pascal triangle to ensure minimum completeness.In Eq.(17),a(x)is the following vector of coefficients

We can obtain the coefficient a by minimizing the following weighted discreteL2-norm[Liu and Gu(2005)]

in whichMis the number of nodes in the support domain of x for which the weight functionanduiis value ofuat x=xi.The stationarity ofJwith respect to a(x)gives[Liu and Gu(2005)]

which leads to the following set of linear equations

in which the vector Usis to the following form

and A(x)is called the weighted moment matrix defined as[Liu and Gu(2005)]

Also the matrix B in Eq.(21)is to the following form[Liu and Gu(2005)]
Now,we solve Eq.(21)for a(x)and arrive at

Substituting the above relation in Eq.(17)we get[Liu and Gu(2005)]

where Φ(x)is the vector of MLS shape functions corresponding toMnodes in the support domain of the point x and we can write[Liu and Gu(2005)]

The shape function φi(x)for theith node is defined by

We use the quartic spline function as the wight function in MLS approximation

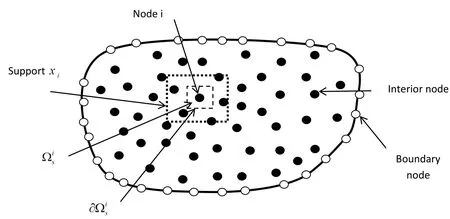
Figure 1:Local boundaries and the domain of definition of MLS approximation
5.1 Formulation of meshless methods based on local weak form
The MLPG method is constructed based on the weak form over local sub-domain such as Ωsthat is a small region considered for any point in the global domain.
in which the local sub-domains overlap each other.Figure 1,which is taken from Liu and Gu(2005)illustrates more explanations corresponding to the local boundaries and the domain of definition of MLS approximation.The local sub-domains for any region have different geometric shapes such as circle and rectangular.In this paper we use rectangular shape for any sub-domain.The local weak form of the time discrete scheme(13)is to the following form:
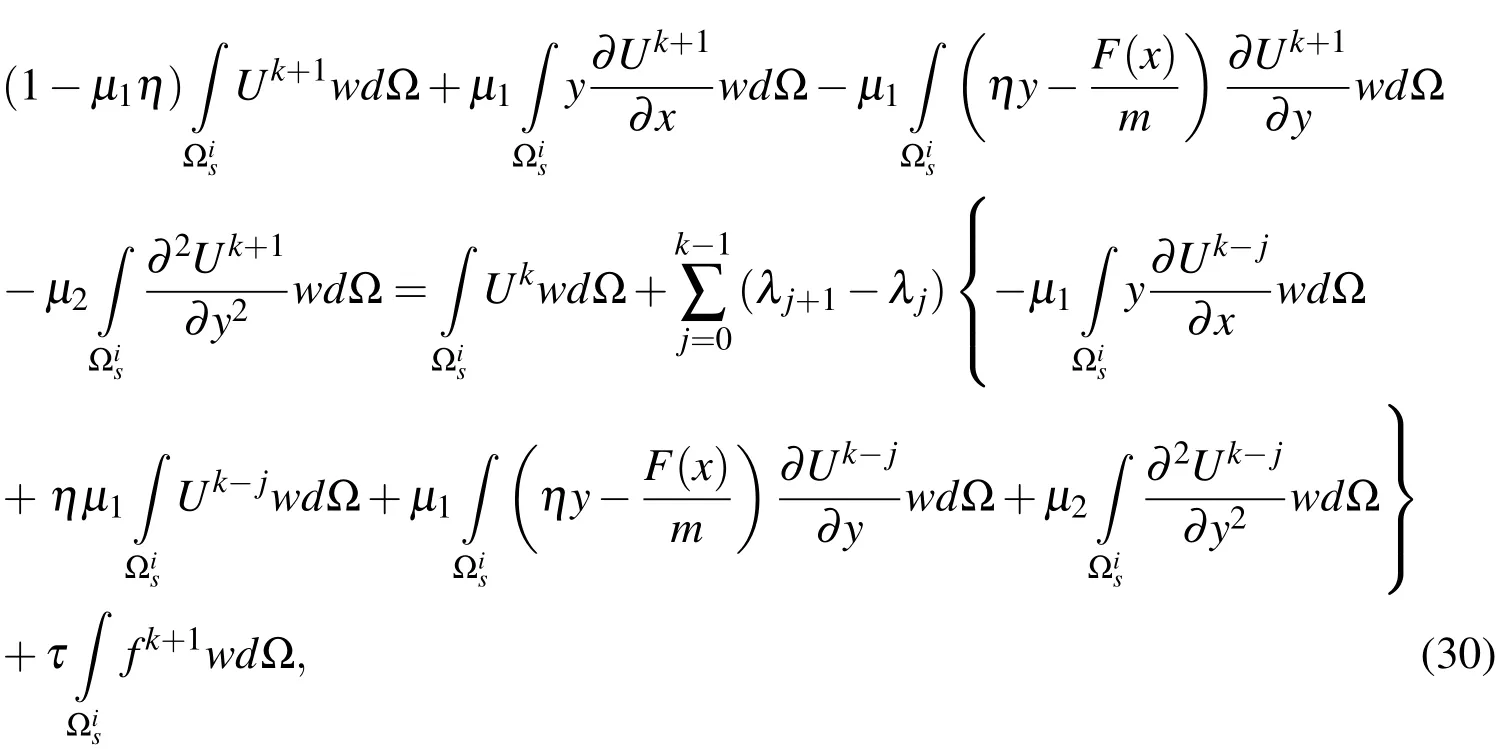
wherewis the test function and we consider the quartic spline function(29)andis a rectangular domain over the pointi.Now,we selectMnodal points on the considered domain that some of them are on the boundary of domain.Substituting the approximate formula(26)into the local integral equation(30)yields
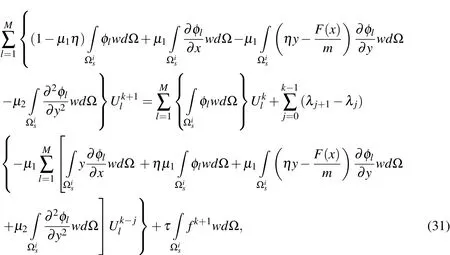

Note for evaluating the integrals that appear in the MLPG method,we use the 8-points Gauss integration quadrature.
6 Numerical results
In this section we present the numerical results of the proposed methods on some test problems.We test the accuracy and stability of the method described in this paper by performing the mentioned scheme for different values ofhand τ.We performed our computations using Matlab 7 software on a Pentium IV,2800 MHz CPU machine with 2 Gbyte of memory.
In this paper,we compute the following error norms
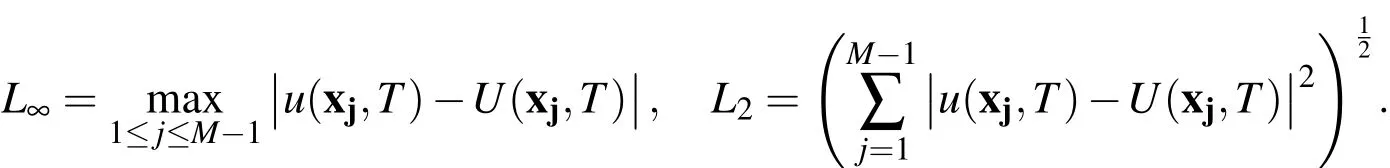
We calculate the computational orders of the method presented in this article with the following formula[Cui(2009);Dehghan and Mohebbi(2008);Mohebbi and
Dehghan(2009)]
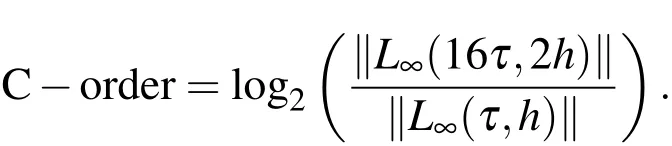
We solve the problem on t?he regions Ω1={(x?,y):0≤x,y≤ 1},Ω2={(x,y):−0.5≤x,y≤0.5},Ω3=(x,y):x2+y2≤1and Ω4={(x,y):y≥0,y+x≤1,y−x≤1}.
6.1 Test problem 1
We consider Eq.(2)with the following form

in which
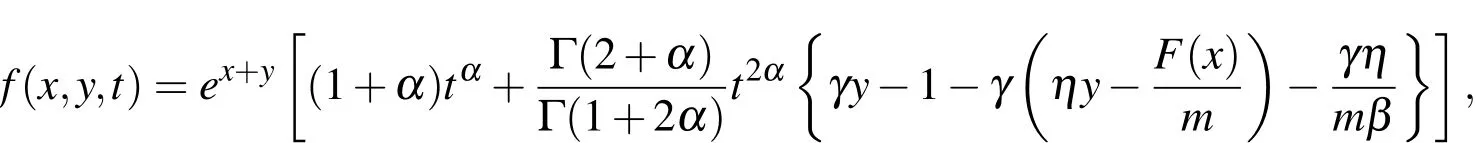
where the exact solution is

also,γ=β=η=m=1 andF(x)=x2.The initial and boundary conditions can be obtained from the exact solution.We solve this problem with the method presented in this article with several values ofh,τ and α forL=1 at final timeT=1 on the rectangular domain Ω1.

Table 1:Errors obtained for Test problem 1 with h=1/10 and α=0.5
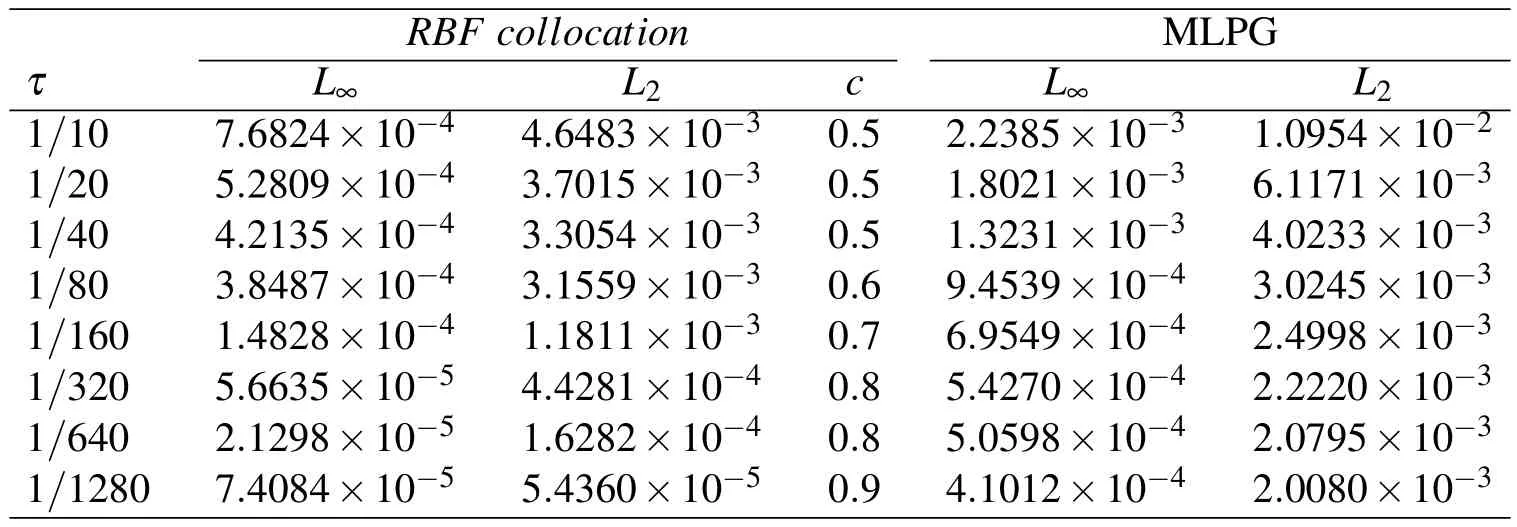
Table 2:Errors obtained for Test problem 1 with h=1/10 and α=0.1

Table 3:Errors and computational orders obtained with α=0.25 for Test problem 1
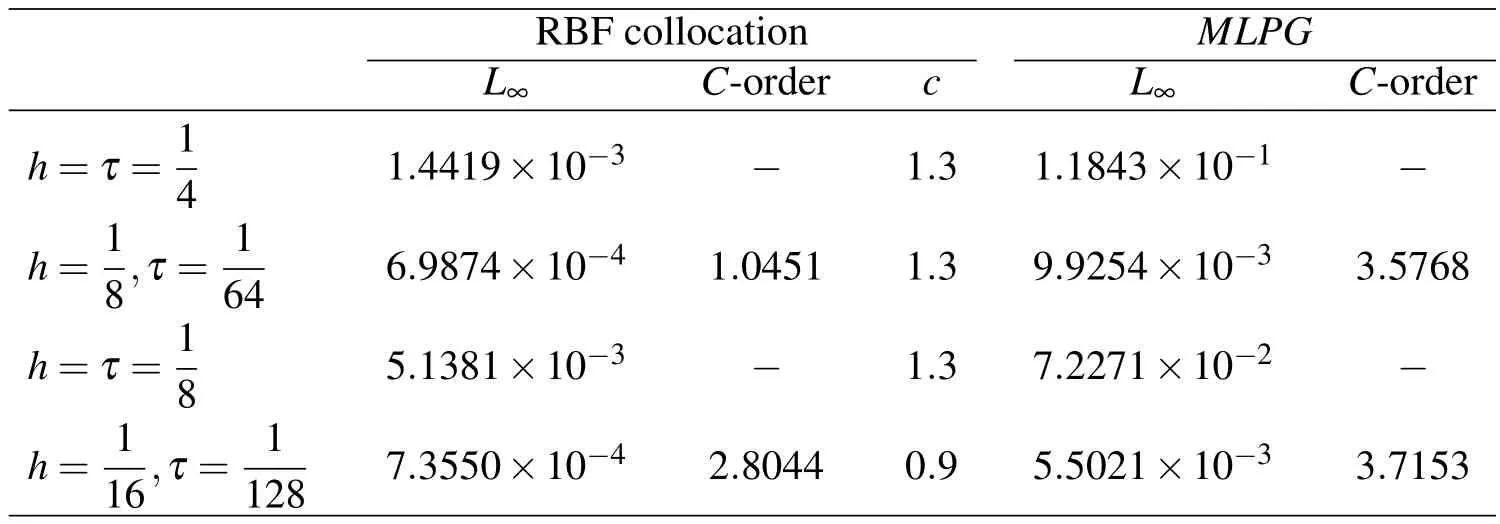
Table 4:Errors and computational orders obtained with α=0.75 for Test problem 1
Tables 1–4 show the errors obtained using the methods proposed in this article for Test problem 1.In these tables,we reported values of errorsL∞andL2.Also,
Tables 3 and 4 show the errors and computational orders obtained for Test problem 1.Figure 2 shows the plots of approximate solution and absolute error using the MLPG technique with α =0.1,h=1/10,τ=1/64 andc=0.1 for Test problem 1.The graphs of approximate solution and absolute error using RBF collocation method with α =0.35,τ=1/64 andc=0.5 on non-rectangular domain are shown in Figure 3 for Test problem 1.Figure 4 shows the irregular domain considered for Figure 3.
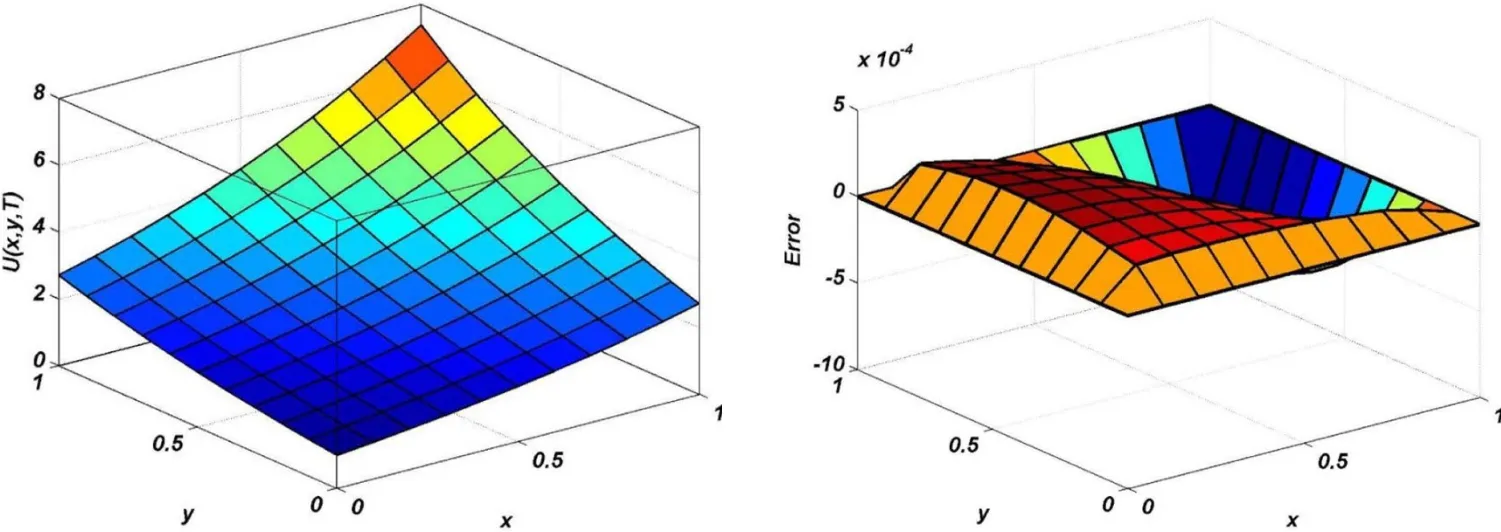
Figure 2:Graphs of approximate solution and absolute error using MLPG method with α =0.1,h=1/10,τ=1/64 and c=0.1 for Test problem 1.
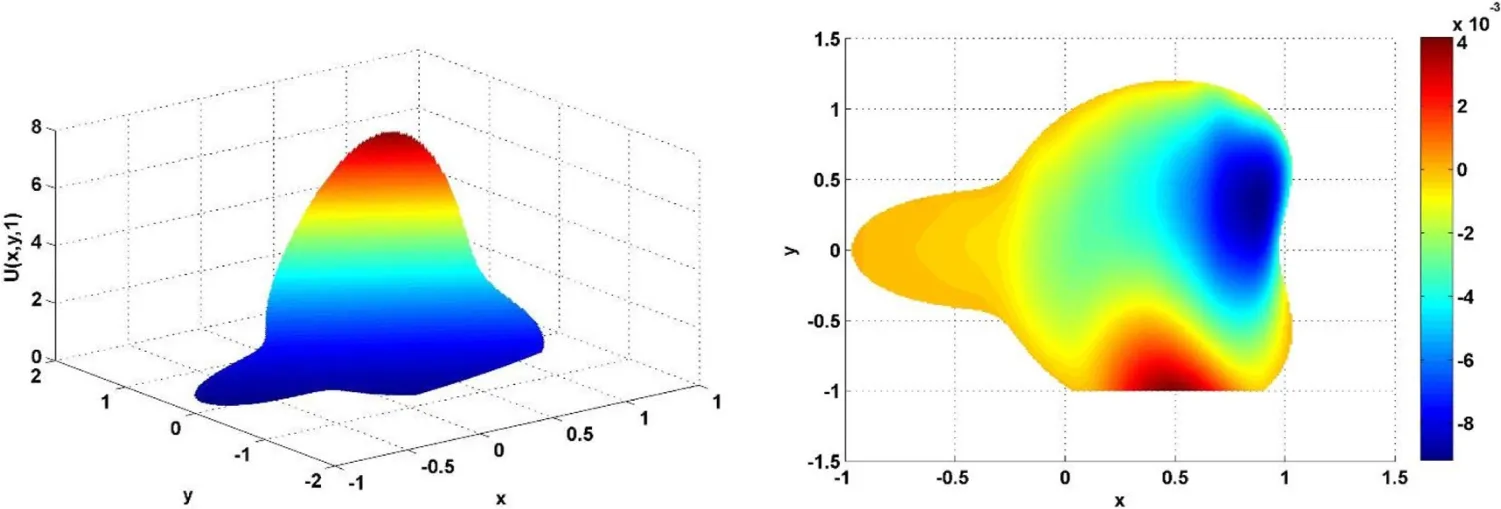
Figure 3:Graphs of approximate solution and absolute error on non-rectangular domain with α =0.35,τ=1/64 and c=0.5 using RBF collocation method for Test problem 1.
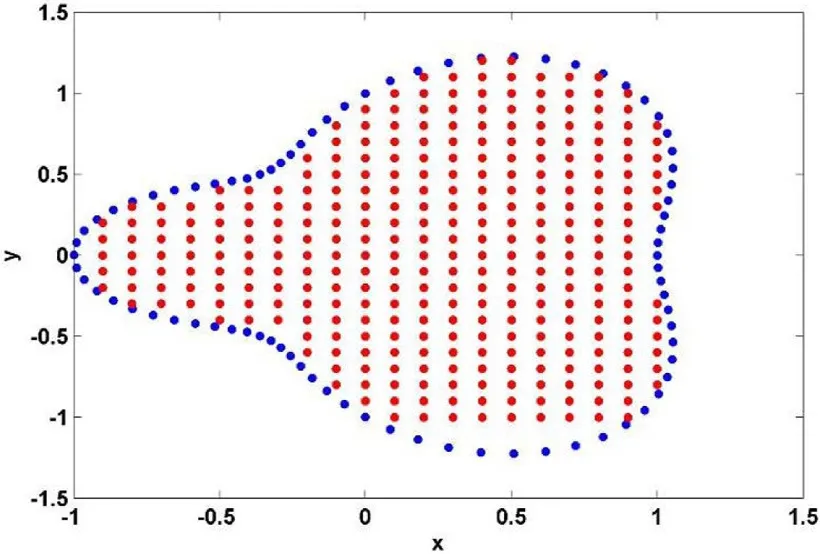
Figure 4:The irregular domain considered for Figure 3
6.2 Test problem 2
We consider the 2D fractional Klein-Kremers equation to the following form

where

The exact solution is a Gaussian pulse witht3hight centered atx=0.5 andy=0.5 to the following form
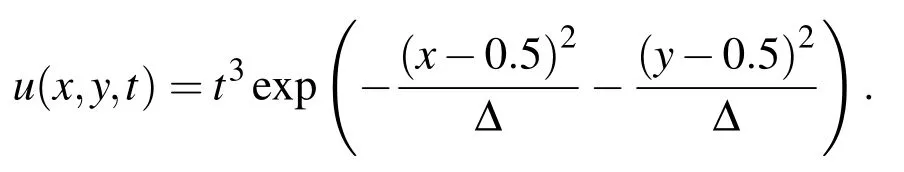
The initial and boundary conditions can be obtained from the exact solution.We solve this problem with the method presented in this article using several values ofh,τ and α at final timeT=1.TheRMS,L∞andL2errors andC-order are shown in Tables 5–8 on the rectangular domain Ω1.

Figure 5:Graphs of approximate solution and its error with on irregular domain α =0.25,τ=1/100,c=0.25 and T=1 when Δ =1/50 using RBF collocation method for Test problem 2.
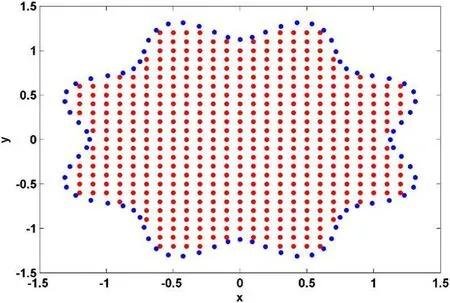
Figure 6:The irregular domain considered for Figure 5
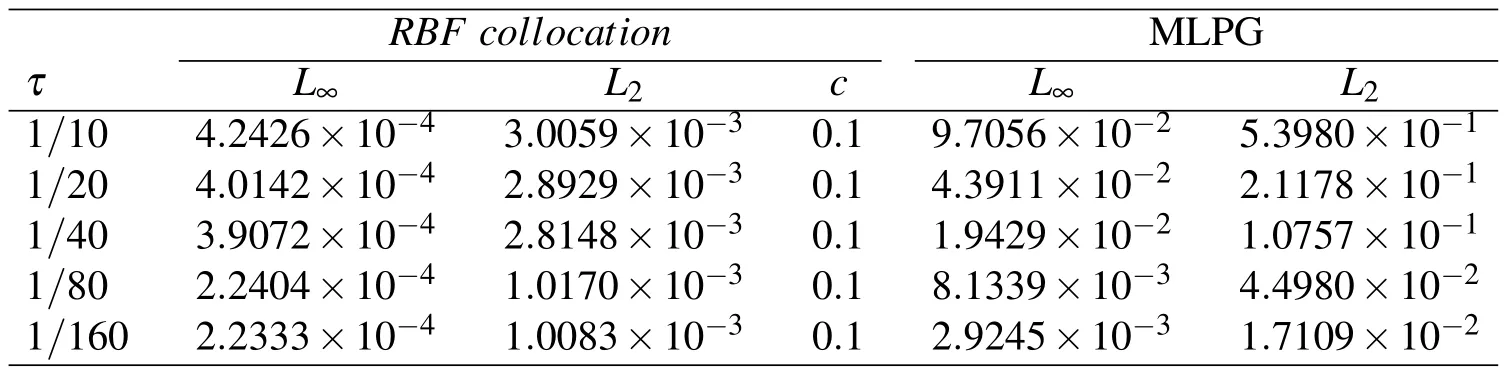
Table 5:Errors obtained for Test problem 1 with h=1/10 and α=0.15
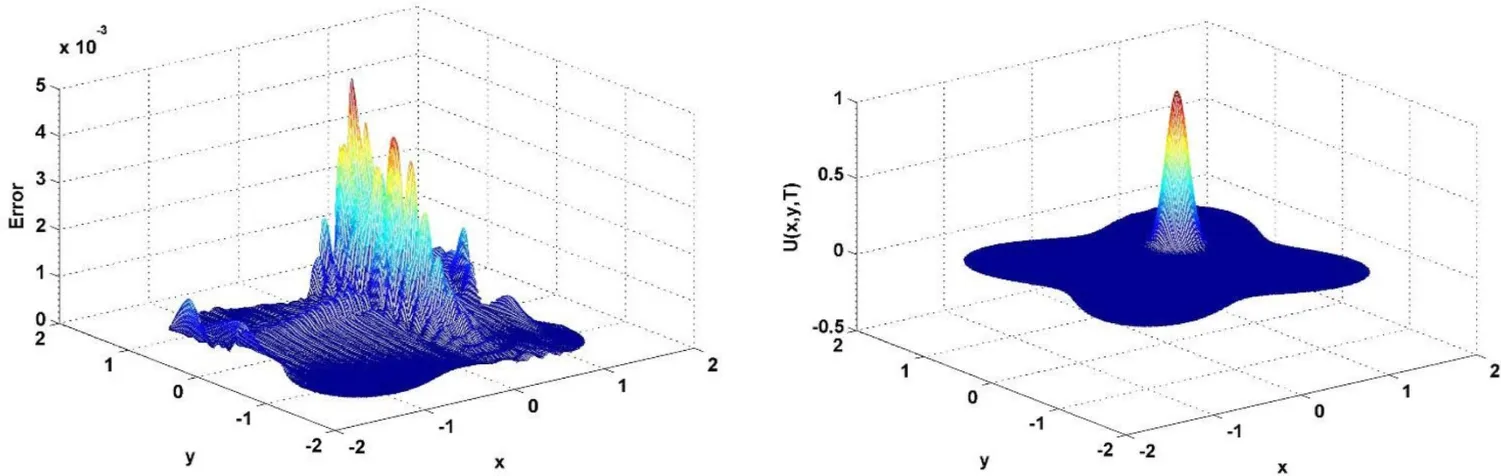
Figure 7:Graphs of approximate solution and its error on irregular domain with α =0.75,τ=1/100,c=0.5 and T=1 when Δ =1/50 using RBF collocation method for Test problem 2.

Figure 8:The irregular domain considered for Figure 7
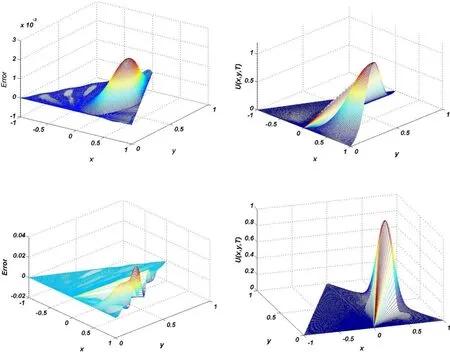
Figure 9:Graphs of approximate solution and its error on the triangular domain Ω4 with α =0.25,h=1/10,τ=1/100,c=0.5 and T=1 when Δ =1/10(a)and Δ=1/50(b)using RBF collocation method for Test problem 2.

Table 7:Errors and computational orders obtained with α=0.35 for Test problem 1
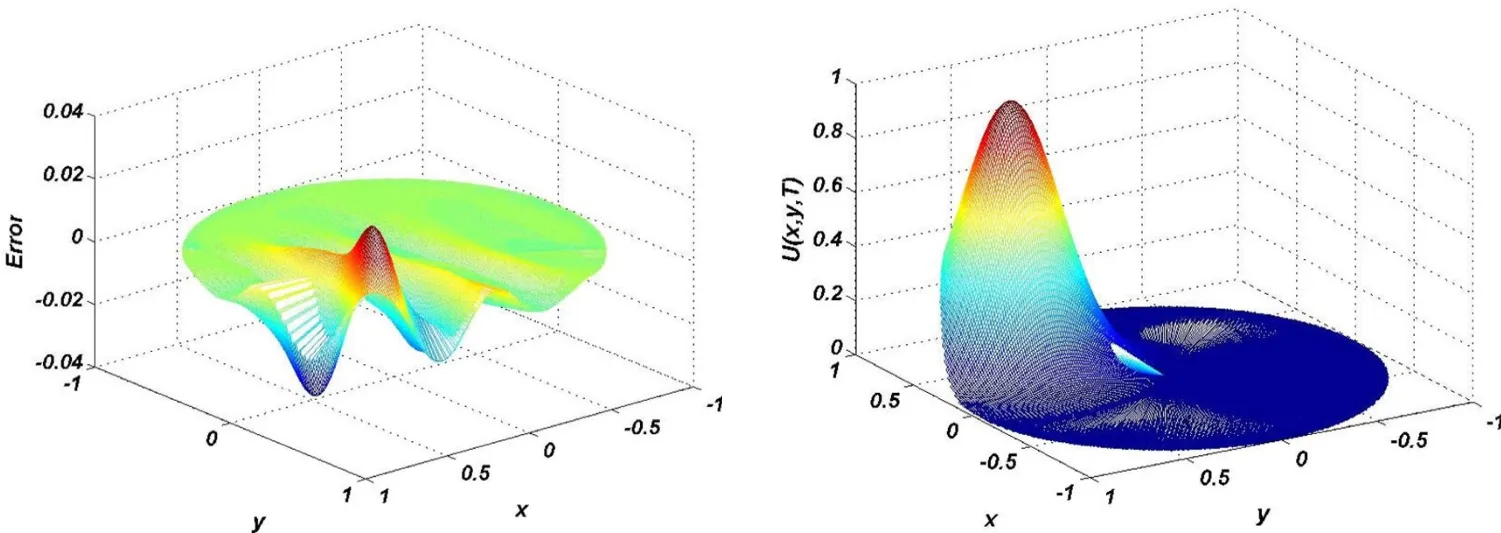
Figure 10:Graphs of approximate solution and its error on the circular domain Ω3 with α =0.25,h=1/10,τ=1/100,c=0.25,T=1 and Δ =1/10 using RBF collocation method for Test problem 2.

Table 8:Errors and computational orders obtained with α=0.55 for Test problem 1
The graphs of approximate solution and its error with α =0.25,τ=1/100,c=0.25 andT=1 when Δ=1/50 and irregular domain for Test problem 2 are shown in Figure 5.Figure 6 is the domain considered for Figure 5.Figure 7 presents the graphs of approximate solution and its error with α =0.75,τ=1/100,c=0.5 andT=1 whenΔ=1/50and on irregular domainfor Testproblem 2.Also,thedomain considered for Figure 7 is demonstrated in Figure 8.Figure 9 shows the graphs of approximate solution and its error on the triangular domain Ω4with α =0.25,h=1/10,τ=1/100,c=0.5 andT=1 when Δ =1/10(a)and Δ =1/50(b)for Test problem 2.Also,Figure 10 shows the graphs of approximate solution and its error on the circular domain Ω3with α =0.25,h=1/10,τ=1/100,c=0.25,T=1 and Δ=1/10 for Test problem 2.Tables 5-8 show the errors obtained using the methods introduced in this article on Ω1for Test problem 2.In these tables,we reported the values ofL∞andL2errors.Also,Tables 7 and 8 show the errors and computational orders obtained for Test problem 2.Figure 11 shows the graphs of approximate solution with α =0.1,h=1/40,τ=1/10 andc=0.1 when Δ =1/10(a),Δ =1/50(b),Δ =1/100(c),Δ =1/500(d)on the region Ω1for Test problem 2.

Figure 11:Graphs of approximate solution with α =0.1,h=1/40,τ=1/10 and c=0.1 when Δ =1/10(a),Δ =1/50(b),Δ =1/100(c),Δ =1/500(d)using MLPG method for Test problem 2.
6.3 Test problem 3
We consider Eq.(2)with γ=β =η =m=1,F(x)=x2,initial condition[Deng and Li(2011);Gao and Sun(2012)]
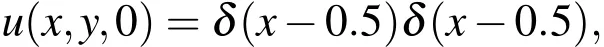
and boundary condition

We obtain the numerical solution of this test where δ (.)denotes the Dirac’s delta function.For implementing the codes,we note that when Δ→0 we have[Gao and
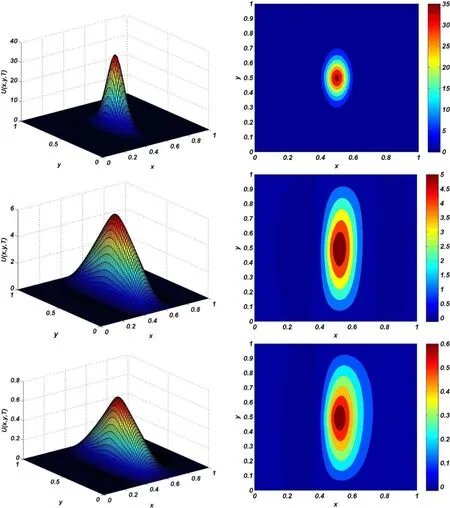
Figure 12:Graphs of approximate solution and its contour with α=0.8,h=1/60,τ=1/10 and c=0.01 when T=0.001(a),T=0.05(b)and T=0.5(c)using RBF collocation method for Test problem 3.
Sun(2012)]
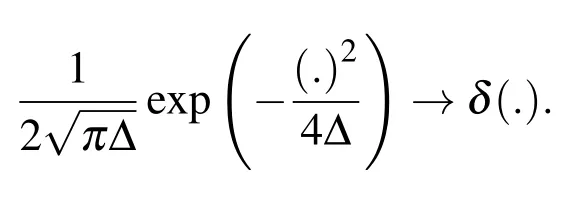
The exact solution for this problem is not available,therefore we solve this model using the new numerical method that proposed in the current paper.Figure 12 shows the graphs of approximate solution and its contour with α=0.8,h=1/60,τ=1/10 andc=0.01 whenT=0.001(a),T=0.05(b)andT=0.5(c)for Test problem 3.Also,Figure 13 shows the value ofU(x,0.5,T)with α=0.8h=1/60,τ=1/10 andc=0.01 whenT=0.001(a)andT=0.005(b)for Test problem 3.As mentioned in[Deng and Li(2011);Gao and Sun(2012)],when final time,T increases the values ofU(x,y,T)decrease.
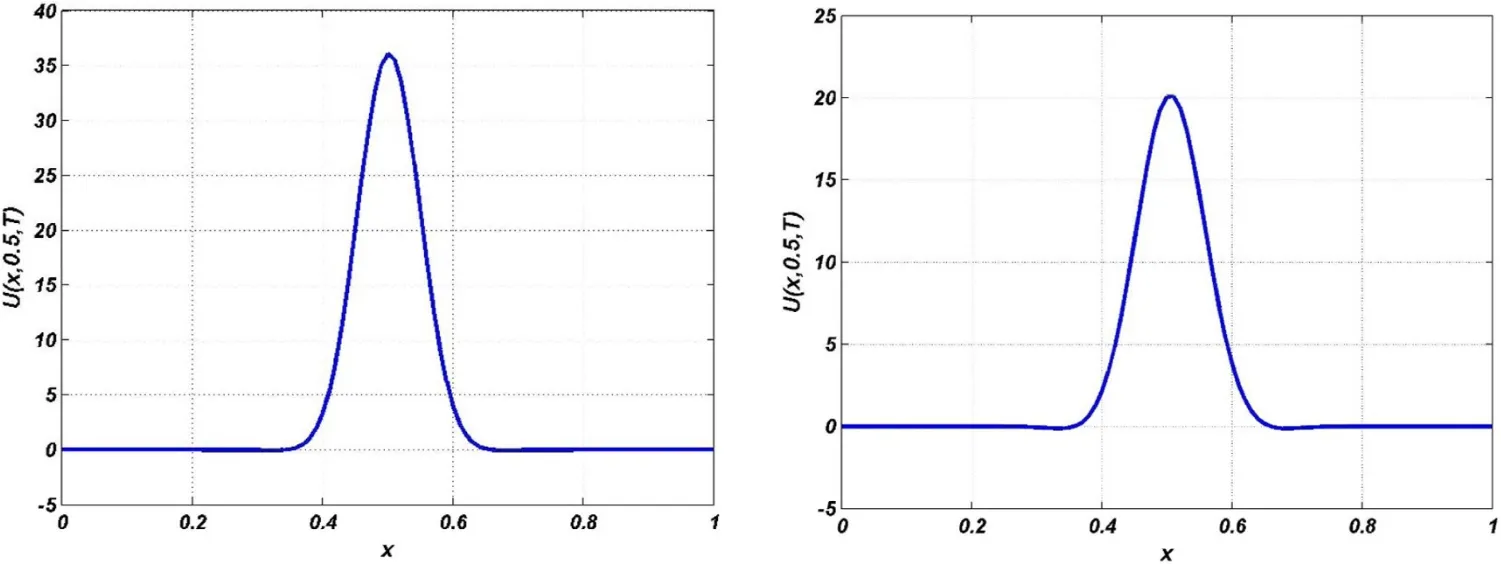
Figure 13:Value of U(x,0.5,T)with α =0.8,h=1/60,τ=1/10 and c=0.01 when T=0.001(a)and T=0.005(b)for Test problem 3.
6.4 Test problem 4
We consider Eq.(2)in which γ= β = η =m=1 andF(x)=x2with initial condition[Deng and Li(2011)]

and boundary condition

Similar to Test problem 3,the exact solution for this problem is not available,thereforewesolvethistestproblemusing numerical method thatdeveloped in thispaper.We obtain the numerical solution of this example where δ(.)denotes the Dirac’s delta function.Figure 14 shows the graphs of approximate solution and its contour with α =0.8,h=1/60,τ=1/10 andc=0.01 whenT=0.001(a),T=0.01(b)for Test problem 4.Also,Figure 15 shows the values ofU(0,y,T)(left panel)andU(x,0,T)(right panel)for Test problem 4.
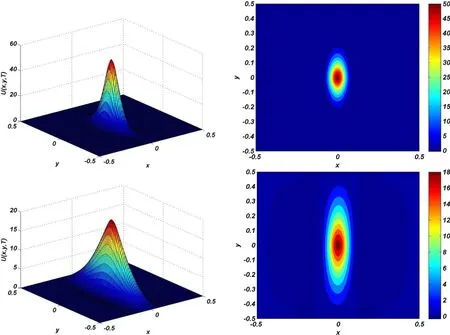
Figure 14:Graphs of approximate solution and its contour with α=0.8,h=1/60,τ=1/10 and c=0.01 when T=0.001(a),T=0.01(b)using MLPG method for Test problem 4.

Figure 15:Values of U(0,y,T)and U(x,0,T)for Test problem 4.
7 Conclusion
In this article,we employed two meshless methods that one of them is based on the strong form i.e.the radial basis functions collocation method and another is based on local weak form i.e.meshless local Petro-Galerkin(MLPG)approach for the solution of the two-dimensional time fractional Klein-Kramers equation.We used a finite difference scheme in time variable.Also we used the radial basis functions based on Kansa method and MLPG technique in space variable.We applied a time discrete scheme for obtaining the approximation of time fractional derivative.The used scheme is based on Riemann-Liouville fractional derivative.We discretized the time fractional derivatives of the mentioned equation by integrating both sides of it.We observed that the convergence order of time discretization for approximating time fractional derivative is O(τ1+γ).Also we solved the mentioned equation on irregular domains.We observed that meshless methods can efficiently solve the mentioned equation on various domains such as triangular and circular domains.Also numerical results confirm the theoretical results of the methods developed in the current paper.
Acknowledgement:The authors are grateful to one of the two reviewers for his(or her)valuable comments and suggestions that improved the paper.
Abbasbandy,S.;Ghehsareh,H.R.;Hashim,I.(2012): Numerical analysis of a mathematical model for capillary formation in tumor angiogenesis using a meshfree method based on the radial basis function.Eng.Anal.Bound.Elem.,vol.36,pp.1811–1818.
Abbasbandy,S.;Ghehsareh,H.R.;Hashim,I.(2013):A meshfree method for the solution of two–dimensional cubic nonlinear Schrodinger equation.Eng.Anal.Bound.Elem.,vol.37,pp.885–898.
Atluri,S.N.(2004):The Meshless Method(MLPG)for Domain and BIE Discretizations.Tech Science Press.
Atluri,S.N.;Shen,S.(2002): The meshless local Petrov-Galerkin(MLPG)method:A simple and less-costly alternative to the finite element and boundary element methods.CMES:Computer Modeling in Engineeringamp;Sciences,vol.3,no.-,pp.11–51.
Atluri,S.N.;Zhu,T.(1998): A new meshless local Petrov-Galerkin(MLPG)approach in computational mechanics.Comput.Mech.,vol.22,pp.117–127.
Bagley,R.;Torvik,P.(1983):A theoretical basis for the application of fractional calculus to viscoelasticity.J.Rheol,vol.27,pp.201–210.
Bicout,D.J.;Berezhkovskii,A.M.(2001):Irreversible bimolecular reactions of Langevin particles.J.Chem.Phys.,vol.114,pp.2293–2303.
Cartling,B.(1987):Kinetics of activated processes from nonstationary solutions of the Fokker-Planck equation for a bistable potential.J.Chem.Phys.,vol.87,pp.2638–2648.
Chen,S.;Liu,F.;Zhuang,P.H.;Anh,V.(2009):Finite difference approximations for the fractional Fokker-Planck equation.Appl.Math.Model.,vol.33,pp.256–273.
Coffey,W.T.;Kalmykov,Y.P.;Titov,S.V.(2004):Inertial effects in anomalous dielectric relaxation,Journal of Molecular Liquids.Appl.Math.Model.,vol.114,pp.35–41.
Cui,M.(2009): Compact finite difference method for the fractional diffusion equation.J.Comput.Phys.,vol.228,pp.7792–7804.
Cui,M.(2012): Compact alternating direction implicit method for two–dimensional time fractional diffusion equation.J.Comput.Phys.,vol.231,pp.2621–2633.
Cui,M.(2014): A high-order compact exponential scheme for the fractional convection-diffusion equation.J.Comput.Appl.Math.,vol.255,pp.404–416.
Dehghan,M.;Mirzaei,D.(2008):The meshless local Petrov-Galerkin(MLPG)method for thegeneralized two-dimensional non-linear Schrodinger equation.Eng.Anal.Bound.Elem.,vol.32,pp.747–756.
Dehghan,M.;Mohebbi,A.(2008):High-order compact boundary value method for the solution of unsteady convection–diffusion problems.Math.Comput.Simul.,vol.79,pp.683–699.
Dehghan,M.;Salehi,R.(2011): The solitary wave solution of the twodimensional regularized long-wave equation in fluids and plasmas.Comput.Phys.Commun.,vol.182,pp.2540–2549.
Dehghan,M.;Salehi,R.(2014): A meshless local Petrov-Galerkin method for the time-dependent Maxwell equations.J.Comput.Appl.Math.,vol.268,pp.93–110.
Dehghan,M.;Shokri,A.(2007): A numerical method for two-dimensional Schrodinger equation using collocation and radial basis functions.Comput.Math.Appl.,vol.54,pp.136–146.
Dehghan,M.;Shokri,A.(2008):A numerical method for solution of the twodimensional sine-Gordon equation using the radial basis functions.Math.Comput.Simul.,vol.79,pp.700–715.
Dehghan,M.;Tatari,M.(2008): Use of radial basis functions for solving the second-order equation with nonlocal boundary conditions.Numer.Methods Partial Differential Eq.,vol.24,pp.924–938.
Deng,W.(2007): Numerical algorithm for the time fractional Fokker-Planck equation.J.Comput.Phy.,vol.227,pp.1510–1522.
Deng,W.(2008):Finite element method for the space and time fractional Fokker-Planck equations.SIAM.J.Numer.Anal.,vol.47,pp.204–206.
Deng,W.;Chen,M.;Barkai,E.(2015):Numerical algorithms for the forward and backward fractional Feynman-Kac equations.J.Sci.Comput.,vol.62,pp.718–746.
Deng,W.;Li,C.P.(2011): Finite difference methods and their physical constraints for the fractional Klein-Kramers equation.Numer.Methods Partial Differential Eq.,vol.27,pp.1561–1583.
Dieterich,P.;Klages,R.;Preuss,R.;Schwab,A.(2008):Anomalous dynamics of cell migration.Proc.Natl.Acad.Sci.USA,vol.105,pp.459–463.
Diethelm,K.;Ford,N.J.(2002): Analysis of fractional differential equations.J.Math.Anal.Appl.,vol.265,pp.229–248.
Esmaeili,S.;Shamsi,M.(2011): Numerical solution of fractional differential equations with a collocation method based on Muntz polynomials.Comput.Math.Appl.,vol.62,pp.918–929.
Fasshauer,G.E.(2007):Meshfree Approximation Methods with MATLAB.USA,World scientific.
Gao,G.H.;Sun,Z.Z.(2012): A finite difference approach for the initialboundary value problem of the fractional Klein-Kramers equation in phase space.Cent.Eur.J.Math.,vol.10,pp.101–115.
Gu,Y.T.;Zhuang,P.H.;Liu,F.(2010): An advanced implicit meshless approach for the non-linear anomalous subdiffusion equation.CMES:Computer Modeling in Engineeringamp;Sciences,vol.56,no.10,pp.303–334.
Gu,Y.T.;Zhuang,P.H.;Liu,Q.(2011):An advanced meshless method for time fractional diffusion equation.International Journal of Computational Methods,vol.8,pp.653–665.
Hadeler,K.P.;Hillen,T.;Lutscher,F.(2004): The Langevin or Kramers approach to biological modeling.Math.Models Methods Appl.Sci.,vol.14,pp.1561–1583.
Hardy,R.L.(1971): Multiquadric equations of topography and other irregular surfaces.J.Geophys.Res.,vol.76,pp.1705–1915.
Huang,C.S.;Yen,H.D.;Cheng,A.H.D.(2010):On the increasingly flat radial basis function and optimal shape parameter for the solution of elliptic PDEs.Eng.Anal.Bound.Elem.,vol.34,pp.802–809.
Kalmykov,Y.P.;Coffey,W.T.;Titov,S.V.(2006): Thermally activated escape rate for a Brownian particle in a double-well potential for all values of the dissipation.J.Chem.Phys.,vol.124,pp.024107.
Kansa,E.J.(1990):Multiquadrics A scattered data approximation scheme with applications to computational fluid dynamics-II.Comput.Math.Appl.,vol.19,pp.147–161.
Kansa,E.J.(1990):Multiquadrics A scattered data approximation scheme with applications to computational fluid-dynamics:I.Comput.Math.Appl.,vol.19,pp.127–145.
Kansa,E.J.;Aldredge,R.C.;Ling,L.(2009):Numerical simulation of two–dimensional combustion using mesh-free methods.Eng.Anal.Bound.Elem.,vol.33,pp.940–950.
Li,C.;Deng,W.;Wu,Y.(2012):Finite difference approximations and dynamics simulations for the Lévy fractional Klein-Kramers equation.Numer.Methods Partial Differential Eq.,vol.8,pp.1944–1965.
Ling,L.(2012): An adaptive–hybrid meshfree approximation method.Int.J.Numer.Meth.Eng.,vol.89,pp.637–657.
Ling,L.;Kansa,E.J.(2005): A least squares preconditioner for radial basis functions collocation methods.Adv.Comput.Math.,vol.23,pp.31–54.
Ling,L.;Opfer,R.;Schaback,R.(2006): Results on meshless collocation techniques.Eng.Anal.Bound.Elem,vol.30,pp.247–253.
Ling,L.;Schaback,R.(2009): An improved subspace selection algorithm for meshless collocation methods.Int.J.Numer.Meth.Eng.,vol.80,pp.1623–1639.
Liu,F.;Anh,V.;Turner,I.(2004): Numerical solution of the space fractional Fokker-Planck equation.J.Comput.Appl.Math.,vol.166,pp.209–219.
Liu,G.R.;Gu,Y.T.(2005):An Introduction to Meshfree Methods and Their Programmin.Springer Dordrecht,Berlin,Heidelberg,New York.
Liu,Q.;Gu,Y.;Zhuang,P.H.;Liu,F.;Nie,Y.(2011): An implicit RBF meshless approach for time fractional diffusion equations.Comput.Mech.,vol.48,pp.1–12.
Liu,Q.;Liu,F.;Turner,I.;Anh,V.;Gu,Y.T.(2014): A RBF meshless approach for modeling a fractal mobile/immobile transport model.Appl.Math.Comput.,vol.226,pp.336–347.
Magdziarz,M.;Weron,A.(2007):Numerical approach to the fractional Klein-Kramers equation.Phys.Rev.E.,vol.76,pp.066708.
Metzler,R.;Klafter,J.(2000): From a generalized Chapman-Kolmogorov equation to the fractional Klein-Kramers equation.J.Phys.Chem.B,vol.104,pp.3851–3857.
Metzler,R.;Sokolov,I.M.(2000): Superdiffusive Klein-Kramers equation:normal and anomalous time evolution and Levy walk moments.Euro.Phys.Lett.,vol.58,pp.482–488.
Miller,K.S.;Ross,B.(1974):An introductional the fractional calculus and fractional differential equations.New York and London:Academic Press:.
Mirzaei,D.;Dehghan,M.(2010): A meshless based method for solution of integral equations.Appl.Numer.Math.,vol.60,pp.245–262.
Mohebbi,A.;Dehghan,M.(2009):The use of compact boundary value method for the solution of two-dimensional Schrödinger equation.J.Comput.Appl.Math.,vol.225,pp.124–134.
Oldham,K.B.;Spanier,J.(1974):The Fractional Calculus.New York and London:Academic Press.
Oldham,K.B.;Spanier,J.(1974):The Fractional Calculus:Theory and Application of Differentiation and Integration to Arbitrary Order.Academic Press.
Orzeł,S.;Weron,A.(2011):Fractional Klein-Kramersdynamicsfor subdiffusion and Itô formula.J.Stat.Mech.,pg.P01006.
Podulbny,I.(1999):Fractional Differential Equations.New York:Academic Press.
Rippa,S.(1999):An algorithm for selecting a good value for the parameter c in radial basis function interpolation.Adv.Comput.Math.,vol.11,pp.193–210.
Saadatmandi,A.;Dehghan,M.(2010): A new operational matrix for solving fractional-order differential equations.Comput.Math.Appl.,vol.59,pp.1326–1336.
Selinger,J.V.;Titulaer,U.M.(1984):The kinetic boundary layer for the Klein-Kramers equation;a new numerical approach.J.Statist.Phys.,vol.36,pp.293–319.
Shokri,A.;Dehghan,M.(2010): A meshless method the using radial basis functions for numerical solution of the regularized long wave equation.Numer.Methods Partial Differential Eq.,vol.26,pp.1990–2000.
Shokri,A.;Dehghan,M.(2010):A Not-a-Knot meshless method using radial basis functions and predictor-corrector scheme to the numerical solution of improved Boussinesq equation.Comput.Physi.Commun.,vol.181,pp.1990–2000.
Shokri,A.;Dehghan,M.(2012): Meshless method using radial basis functions for the numerical solution of two–dimensional complex Ginzburg-Landau equation.CMES:Computer Modeling in Engineeringamp;Sciences,vol.34,pp.333–358.
Sladek,J.;Sladek,V.;Atluri,S.N.(2000): Local boundary integral equation(LBIE)method for solving problems of elasticity with nonhomogeneous material properties.Comput.Mech.,vol.24,pp.456–462.
Sladek,J.;Sladek,V.;Atluri,S.N.(2004): Meshless local Petrov-Galerkin method for heat conduction problem in an anisotropic medium.CMES:Computer Modeling in Engineeringamp;Sciences,vol.6,pp.309–318.
Sladek,J.;Sladek,V.;Atluri,S.N.(2004): Meshless local Petrov-Galerkin method in anisotropic elasticity.CMES:Computer Modeling in Engineeringamp;Sciences,vol.6,pp.477–490.
Sladek,J.;Sladek,V.;Hellmich,C.H.;Eberhardsteiner,J.(2007): Heat conduction analysis of 3-D axisymmetric and anisotropic FGM bodies by meshless local Petrov-Galerkin method.Comput.Mech.,vol.39,pp.323–333.
Sladek,J.;Sladek,V.;Hon,Y.C.(2006): Inverse heat conduction problems by meshless local Petrov-Galerkin method.Eng.Anal.Bound.Elem.,vol.36,pp.650–661.
Sladek,J.;Sladek,V.;Krivacek,J.;Wen,P.H.;Zhang,C.(2007):Meshless local Petrov-Galerkin(MLPG)method for Reissner-Mindlin plates under dynamic load.Comput.Methods Appl.Mech.Engrg.,vol.196,pp.2681–2691.
Sladek,J.;Sladek,V.;Zhang,C.;Schanz,M.(2006): Meshless local Petrov-Galerkin method for continuously nonhomogeneous linear viscoelastic solids.Comput.Mech.,vol.37,pp.279–289.
Sladek,J.;Stanak,P.;Han,Z.D.;Sladek,V.;Atluri,S.N.(2013): Applications of the MLPG Method in Engineeringamp;Sciences:A Review.CMES:Computer Modeling in Engineeringamp;Sciences,vol.92,no.5,pp.423–475.
Taleei,A.;Dehghan,M.(2014):Direct meshless local Petrov-Galerkin method for elliptic interface problems with applications in electrostatic and elastostatic.Comput.Methods Appl.Mech.Eng.,vol.278,pp.479–498.
Trahan,C.J.;Wyatt,R.E.(2004):Classical and quantum phasespaceevolution:fi xed-lattice and trajectory solutions.Chem.Phys.Lett.,vol.385,pp.280–285.
Vanani,S.K.;Aminataei,A.(2008):On the numerical solution of neural delay differential equations using multiquadric approximation scheme.Bull.Korean Math.Soc.,vol.45,pp.663–670.
Wendland,H.(2005):Scattered Data Approximation.Cambridge University Press.
Wess,W.(1996):The fractional diffusion equation.J.Math.Phys.,vol.27,pp.2782–2785.
Widder,M.E.;Titulaer,U.M.(1993):Kinetic boundary layers in gas mixtures:systems described by nonlinearly coupled kinetic and hydrodynamic equations and applications to droplet condensation and evaporation.J.Stat.Phys.,vol.70,pp.1255–1279.
Zhuang,P.H.;Liu,F.;Anh,V.;Turner,I.(2008): New solution and analytical techniques of the implicit numerical methods for the anomalous sub-diffusion equation.SIAM J.Numer.Anal.,vol.46,pp.1079–1095.
Zhuang,P.H.;Liu,Q.X.(2009):Numerical method of Rayleigh-Stokesproblem for heated generalized second grade fluid with fractional derivative.Appl.Math.Mech.Engl.Ed.,vol.30,pp.1533–1546.
1Department of Applied Mathematics,Faculty of Mathematics and Computer Sciences,Amirkabir University of Technology,No.424,Hafez Ave.,15914,Tehran,Iran,Corresponding author.E-mail addresses:mdehghan@aut.ac.ir,mdehghan.aut@gmail.com,(M.Dehghan)
2Department of Applied Mathematics,Faculty of Mathematics and Computer Sciences,Amirkabir University of Technology,No.424,Hafez Ave.,15914,Tehran,Iran,E-mail addresses:m.abbaszadeh@aut.ac.ir(M.Abbaszadeh)
3Department of Applied Mathematics,Faculty of Mathematical Sciences,University of Kashan,Kashan,Iran.E-mail addresses:a_mohebbi@kashanu.ac.ir(A.Mohebbi).
