Experimental and Numerical Investigation for Membrane Deployment using SPH and ALE Formulations

Essam Al-Bahkali,Hisham Elkenaniand Souli Mhamed

Experimental and Numerical Investigation for Membrane Deployment using SPH and ALE Formulations

Essam Al-Bahkali1,2,Hisham Elkenani1and Souli Mhamed3

Simulation of airbag and membrane deployment under pressurized gas problems becomes more and more the focus of computational engineering,where FEM （Finite element Methods）for structural mechanics and Finite Volume for CFD are dominant.New formulations have been developed for FSI applications using mesh free methods as SPH method,（Smooth Particle Hydrodynamic）.Up to these days very little has been done to compare different methods and assess which one would be more suitable.For small deformation,FEM Lagrangian formulation can solve structure interface and material boundary accurately,the main limitation of the formulation is high mesh distortion for large deformation and moving structure.One of the commonly used approach to solve these problems is the ALE formulation which has been used with success in the simulation of FSI（Fluid Structure Interaction）with large structure motion such as sloshing fuel tank in automotive industry and bird impact in aeronautic industry.For some applications,including bird impact and high velocity impact problems,engineers have switched from ALE to SPH method to reduce CPU time and save memory allocation.In this paper the mathematical and numerical implementation of the ALE and SPH formulations are described.From different simulation,it has been observed that for the SPH method to provide similar results as ALE or Lagrangian formulations,the SPH meshing,or SPH spacing particles needs to be finer than the ALE mesh.To validate the statement,we perform a simulation of membrane deployment generated by high pressurized gas.For this simple problem,the particle spacing of SPH method needs to be at least two times finer than ALE mesh.A contact algorithm is performed at the FSI for both SPH and ALE formulations.

ALE,SPH,FSI,CFD,Hyperelastic.

1 Introduction

Theoretical and experimental analysis of fluid structure interaction for airbag and membrane deployment have been considered by several researchers over the past decades,using uniform pressure methods.The uniform pressure formulation does not consider the gas simulation,and no CFD modeling is involved.Experiments have shown,that the resulting flow is quite complex,involving several physical phenomena as damping effects.Numerical simulation using appropriate hydrodynamic equations for the gas,helps to describe these phenomena,and also minimize the number of tests required that are very costly.Once simulations are validated by test results,it can be used as design tool for the improvement of the system structure involved.Initially FEM Lagrangian were used to simulate these problems,unfortunately classical Lagrangian methods cannot resolve large mesh distortion,runs are stopped before reaching termination time,due to negative Jacobian in highly distorted element.ALE multi-material description of motion developed in Aquelet,Souli and Olovson （2005）can be used as an alternative for the simulation of high explosive phenomena.The ALE formulations have been developed to overcome the difficulties due to large mesh distortion.For some applications,including underwater explosions and their impact on the surrounding structure,engineers have switched from ALE to SPH method to reduce CPU time and save memory allocation.

It is well known from previous papers,see Ozdemir,Souli and Fahjan （2010）that the classical FEM Lagrangian method is not suitable for most of the FSI problems due to high mesh distortion in the fluid domain.In many applications the ALE formulation has been the only alternative to solve fluid structure interaction for engineering problems.For the last decade,SPH method has been usefully used for engineering problems to simulate high velocity impact problems,high explosive detonation in soil,underwater explosion phenomena,and bird strike in aerospace industry.SPH is a mesh free Lagrangian description of motion,that can provide many advantages in fluid mechanics and also for modeling large deformation in solid mechanics.Unlike ALE method,and because of the absence of the mesh,SPH method suffers from a lack of consistency than can lead to poor accuracy.In the literature there are different formulations of meshless methods,the Meshless Local Petrov-Galerkin Method for solving the bending problem of a thin,see Han and Atluri（2014）and Shuyao and Atluri（2002）and also Meshless Finite Volume Method developed for solving elasto-static,see Alturi,Han,and Rajendran （2004）.In Meshless Local Petrov-Galerkin Method mixed approach,both the strains as well as displacements are interpolated,at randomly distributed points in the domain,through local meshless interpolation schemes such as the moving least squares or radial basis functions.In this paper,devoted to ALE and SPH formulations for fluid structure interaction problems,the mathematical and numerical implementation of the ALE and SPH formulations are described.From different simulation,it has been observed that for the SPH method to provide similar results as ALE formulation,the SPH meshing,or SPH spacing particles needs to be finer than the ALE mesh.To validate the statement„we perform a simulation of a membrane deployment generated by pressurized gas.For this problem,the particle spacing of SPH method needs to be at least two times finer than ALE mesh.A contact algorithm is performed at the fluid structure interface for both SPH and ALE formulations.

In Section 2,the governing equations of the ALE formulation are described.In this section,we discuss the advection algorithms used to solve mass,momentum and energy conservation in the multi-material formulation.Section 3 describes the SPH formulation,unlike ALE formulation which based of the Galerkin approach,SPH is a collocation method.The last section is devoted to numerical simulation of a membrane deployment under high pressurized gas,using both ALE and SPH methods.The numerical results will be compared to experimental data.

2 ALE Formulation

Fluid problems,in which interfaces between different materials（gas and ambient air）are present,are more easily modeled by using a Lagrangian mesh.However,if an analysis for complex tank geometry is required,the distortion of the Lagrangian mesh makes such a method difficult to use many re-meshing steps are necessary for the calculation to continue.Another method to use is the Eulerian formulation.This change from a Lagrangian to an Eulerian formulation,however,introduces two problems.The first problem is the interface tracking[Hallquist（1998）]and the second problem is the advection phase or advection of fluid material across element boundaries.

To solve these problems,an explicit finite element method for the Lagrangian phase and a finite volume method （flux method）for the advection phase are used.We can refer to several explicit codes such as Pronto,Dyna3D and LS-DYNA;see Von Neumann and Richtmeyer （1950）for a full description of the explicit finite element method.The advection phase has been developed for extending the range of applications that cannot be used with the Lagrangian formulation.Current applications include sloshing involving a ‘free surface’,and high velocity impact problems where the target is modeled as a fluid material,thus providing a more realistic representation of the impact event by capturing large deformations.

An ALE formulation contains both pure Lagrangian and pure Eulerian formulations.The pure Lagrangian description is the approach that:the mesh moves with the material,making it easy to track interfaces and to apply boundary conditions.Using an Eulerian description,the mesh remains fixed while the material passes through it.Interfaces and boundary conditions are difficult to track using this approach;however,mesh distortion is not a problem because the mesh never changes.In solid mechanics a pure Eulerian formulation it is not useful because it can handle only a single material in an element,while an ALE formulation is assumed to be capable of handling more than one material in an element.

In the ALE description,an arbitrary referential coordinate is introduced in addition to the Lagrangian and Eulerian coordinates.The material derivative with respect to the reference coordinate can be described in Eq. （1）.Thus substituting the relationship between the material time derivative and the reference configuration time derivative derives the ALE equations.

whereXiis the Lagrangian coordinate,xithe Eulerian coordinate,wiis the relative velocity.Let denote byvthe velocity of the material and byuthe velocity of the mesh.In order to simplify the equations we introduce the relative velocityw=v-u.Thus the governing equations for the ALE formulation are given by the following conservation Eqs.（2）to （4）:

（i）Mass equation.

（ii）Momentum equation.

The strong form of the problem governing Newtonian fluid flow in a fixed domain consists of the governing equations and suitable initial and boundary conditions.The equations governing the fluid problem are the ALE description of the Navier-Stokes equations:

Boundary and initial conditions need to be imposed for the problem to be well posed.

The superscript means prescribed value,niis the outward unit normal vector on the boundary,and δijis Kronecker’s delta function.

（iii）Energy equation.

Note that the Eulerian equations commonly used in fluid mechanics by the CFD community,are derived by assuming that the velocity of the reference configuration is zero and that the relative velocity between the material and the reference configuration is therefore the material velocity.The term in the relative velocity in Eqs. （3）and （4）is usually referred to as the advective term,and accounts for the transport of the material past the mesh.It is the additional term in the equations that makes solving the ALE equations much more difficult numerically than the Lagrangian equations,where the relative velocity is zero.

In the second phase,the advection phase,transport of mass,internal energy and momentum across cell boundaries are computed;this may be thought of as remapping the displaced mesh at the Lagrangian phase back to its original or arbitrary position.

From a discretization point of view of Eqs.（2）,（3）and （4）,one point integration is used for efficiency and to eliminate locking,.The zero energy modes are controlled with an hourglass viscosity Benson,see Libersky,Petschek,Carney,Hipp,and Allahdadi（1993）.A shock viscosity,with linear and quadratic terms,is used to resolve the shock wave,see Lucy （1977）;a pressure term is added to the pressure in the energy Eq.（4）.The resolution is advanced in time with the central difference method,which provides a second order accuracy in time using an explicit method in time.For each node,the velocity and displacement are updated as follows:

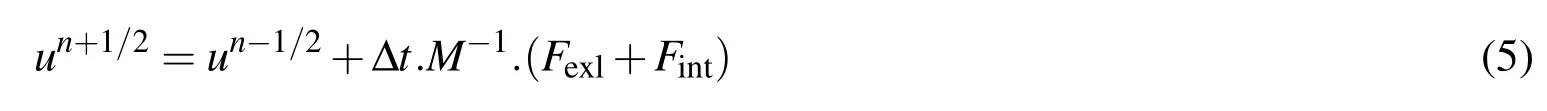
The multi-material formulation is attractive for solving a broad range of non-linear problems in fluid and solid mechanics,because it allows arbitrary large deformations and enables free surfaces to evolve.The Lagrangian phase of the VOF method is easily implemented in an explicit ALE finite element method.Before advection,special treatment for the partially voided element is needed.For an element that is partially filled,the volume fraction satisfiesVf≤ 1,and the total stress by σ is weighed by volume fraction σf= σ.Vf.

In the second phase,the transport of mass,momentum and internal energy across the element boundaries is computed.This phase may be considered as a‘remapping’phase.The displaced mesh from the Lagrangian phase is remapped into the initial mesh for an Eulerian formulation,or an arbitrary undistorted mesh for an ALE formulation.

In this advection phase,we solve a hyperbolic problem,or a transport problem,where the variables are density,momentum and internal energy per unit volume,where the Donor Cell algorithm,a first order advection method and the Van Leer algorithm,a second order advection method,see Von Neumann and Richtmeyer（1950）,are used.As an example,the equation for mass conservation is:

It is not the goal of this paper to describe the different algorithms used to solve Eq.（7）.Fig.1 describes the two phases for a one step explicit calculation.

Figure 1:Lagrangian and Advection phases in multi-material ALE formulation.

3 SPH Formulation

The SPH method developed originally for solving astrophysics problem has been extended to solid mechanics by Libersky,Petschek,Carney,Hipp,and Allahdadi（1993）to model problems involving large deformation including high velocity impact.SPH method provides many advantages in modeling severe deformation as compared to classical FEM formulation which suffers from high mesh distortion,Fig.2.The method was first introduced by Lucy （1977）and Gingold and Monaghan （1977）for gas dynamic problems and for problems where the main concern is a set of discrete physical particles than the continuum media.The method was extended to solve high velocity impact in solid mechanics,CFD applications governed by Navier-Stokes equations and fluid structure interaction problems.

It is well known from previous papers,that SPH method suffers from lack of consistency,that can lead to poor accuracy of motion approximation.Unlike Finite Element,interpolation in SPH method cannot reproduce constant and linear functions.

A detailed overview of the SPH method is developed by Liu and Liu （2010）,where the two steps for representing of function f,an integral interpolation and a kernel approximation are given by:

Figure 2:FEM model,mesh and nodes （left）and SPH model,particles （right）

where the Dirac function satisfies:

The approximation of the integral function Eq. （7）is based on the kernel approximation W,which approximates the Dirac function based on the smoothing length h.

that represents support domain of the kernel function,see Fig.3.

Figure 3:Kernel Function and its support domain for a 2D function.

So that Eq.（7）becomes,

Taking in consideration de support domain of the kernel function,the SPH approximation of a particlexiis obtained discretizing the integral into a sum over the particles that are within the kernel support domain as it is shown in Fig.3.

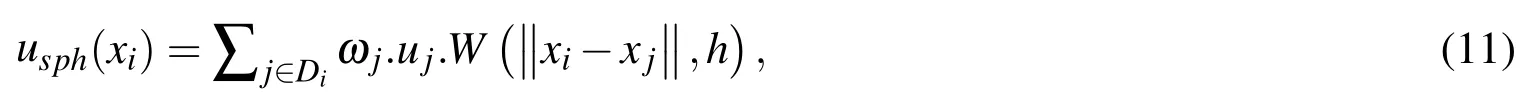
Integrating by part Eq.3.4 and considering the properties of the SPH interpolation and that∇（u）=u.∇（1）-1.∇（u）,the SPH approximation for the gradient operator of a function is given by,

（ii）Momentum equation.

（iii）Energy equation.

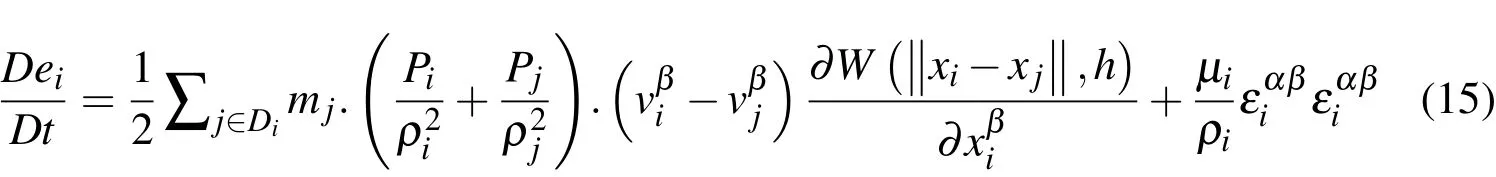
4 ALE Penalty Coupling Algorithm

Penalty coupling behaves like a spring system and penalty forces are calculated proportionally to the penetration depth and spring stiffness.The head of the spring is attached to the structure or slave node and the tail of the spring is attached to the master node within a fluid element that is intercepted by the structure,as illustrated in Fig.4.

Similarly to penalty contact algorithm,the coupling force is described by （16）:

wherekrepresents the spring stiffness,anddthe penetration.The forceFin Fig.4 is applied to both master and slave nodes in opposite directions to satisfy force equilibrium at the interface coupling,and thus the coupling is consistent with the fluid-structure interface conditions namely the action-reaction principle.

The main difficulty in the coupling problem comes from the evaluation of the stiffness coefficientkin Eq. （16）.The stiffness value is problem dependent,a good value for the stiffness should reduce energy interface in order to satisfy total energy conservation,and prevent fluid leakage through the structure.The value of the stiffnesskis still a research topic for explicit contact-impact algorithms in structural mechanics.In this paper,the stiffness value is similar to the one used in Lagrangian explicit contact algorithms,described in Benson （1992）.The value ofkis given in term of the bulk modulusKof the fluid element in the coupling containing the slave structure node,the volumeVof the fluid element that contains the master fluid node,and the average areaAof the structure element connected to the structure node.

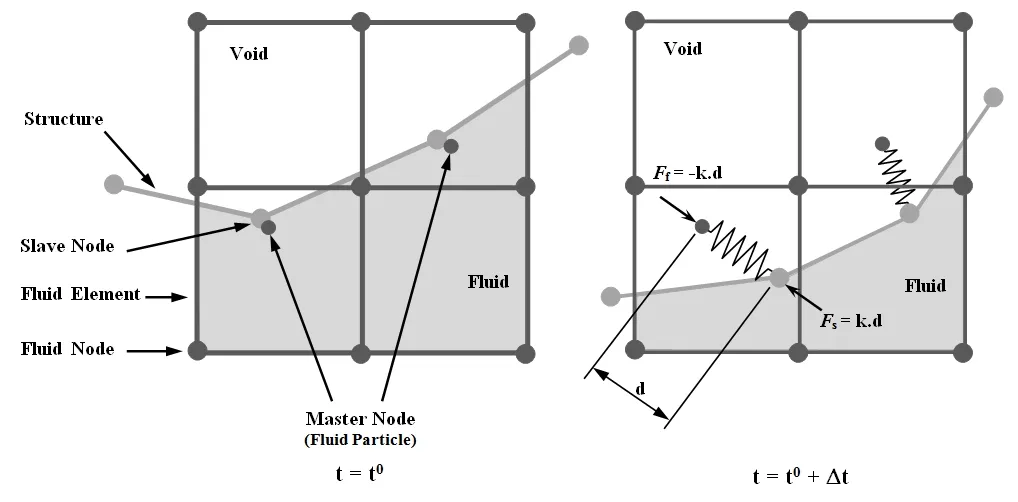
Figure 4:Description of Penalty Coupling Algorithm.

5 SPH Contact Algorithm

Several contact methods have been published in litterarture between different structure material parts.Classical implicitand explicit coupling aredescribedin detail in Longatte,Bendjeddou,and Souli M.（2003）and Longatte,Verreman,and Souli M.（2009）,where hydrodynamic forces from the fluid solver are passed to the structure solver for stress and displacement computation.In this paper,a coupling method based on contact algorithm is used.Since the coupling method described in this chapter is based on the penalty method for contact algorithms,the contact approach is a good introduction to this method.In contact algorithms,a contact force is computed proportional to the penetration vector,the amount the constraint is violated.In contact algorithms,one surface is designated as a slave surface,and the second as a master surface.The nodes lying on both surfaces are also called slave and master nodes respectively.In an explicit FEM method,contact algorithms compute interface forces due to impact of the slave node on the master node,these forces are applied to the slave and master nodes in contact in order to prevent a node from passing through contact interface.The penalty method imposes a resisting force to the slave node,proportional to its penetration through the master segment,as shown in Fig.5 describing the contact process.This force is applied to both the slave node and the nodes of the master segment in opposite directions to satisfy equilibrium.

Figure 5:Description of Penalty Contact algorithm between slave particle and master structure.

6 Description of the Experimental Setup

Erchiqui,Derdouri,Gakwaya,and Verron （2001）experimentally investigated the inflation behavior in a thermoplastic membrane under the combined effects of applied stress and temperature using bubble inflation tests.The results were used to identify the material constants embedded in the constitutive models of the polymeric materials in this work.The polymeric material,acrylonitrile-butadienestyrene （ABS）,was tested under biaxial deformation using the bubble inflation technique.The initial ABS sheet thickness was 1.57 mm.The experimental setup is shown in Fig.6.

The circular membranes were mounted between two metal disks containing a circular aperture and subsequently clamped onto a support.The exposed circular area of diameter D=6.35 cm was heated in an infrared heating chamber to the softening point.When the temperature became uniform over the flat sheet,the circular area was inflated using compressed air under a controlled flow rate.The applied inflation pressure,which was uniform over the membrane,was measured with a pressure sensor during the testing.The height at the hemispheric pole（or the center of the membrane）and the time were recorded simultaneously using a video camera and a data acquisition system.For most inflation tests,testing ends when the bubble bursts.

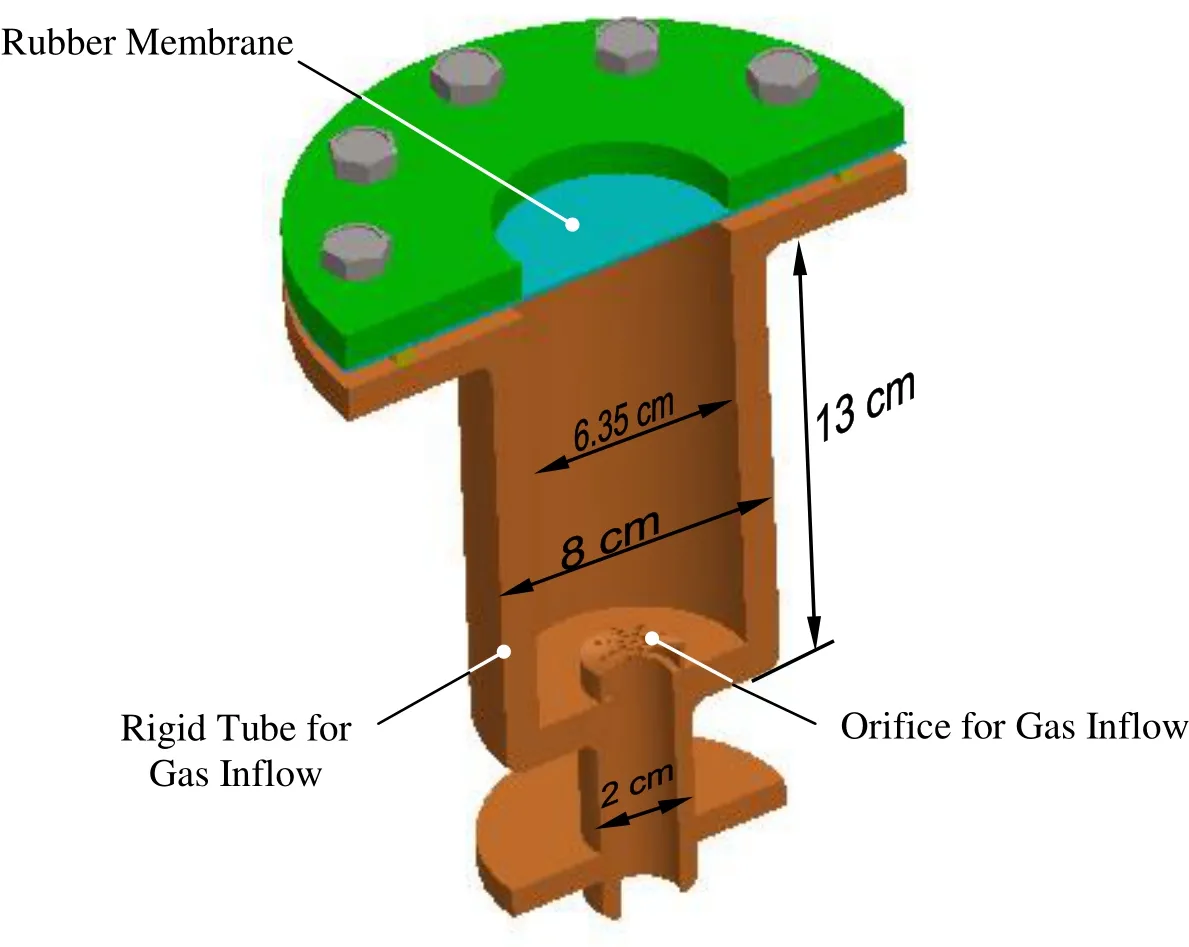
Figure 6:Test rig used in the experiment.

7 Numerical Simulation using SPH Method

The next subsections describe the model set up including all simulation approaches used as well as the boundary conditions applied to the model.

7.1 Meshing and Material Modeling

The model,as shown in Fig.7,consists of four parts,a membrane,fluid domain,sidewall,and a rigid plate acts as a piston.The fluid domain in this case has the property of air.Table 1 denotes the details of the property values.

Figure 7:Model used for membrane inflation simulation.

Table 1:Properties of air used in this paper.

The membrane is modeled using acrylonitrile-butadiene-styrene （ABS）.The material constants for Moony-Rivlin model are C10=105000 Pa and C01=10500 Pa,see Souli and Zolesio （1993）,corresponding to α=0.1 （α =C01/C10）.The theoretical material constants are obtained by fitting pressure deformation experimental data with a membrane radius of 0.03175 m and a sheet thickness of 0.00157 m.Fitting curves for various values for α of isotropic hyperelastic model at 143˚C shows that the value of α=10 is the best fit for the experimental data.

The membrane is meshed with shell elements.For the air,to ensure uniform distribution for the air particles using SPH method,it initially meshed with solid elements,and then conversion functionality is used to convert the solid element into SPH particles,Fig.8.

Table 2:Mesh Detailed Report.

Figure 8:Element conversion from FEM mesh to SPH particles.

We can also specify the time when the conversion of all the elements in the affected element set is to take place.In our case,the conversion time is specified as zero,then the conversion takes place at the beginning of the analysis.

The rigid plate which is acts as a piston is modeled as a rigid body as there is no need to introduce it in the solution.It just acts as inflator’s piston.So,no material assigned to it.

7.2 Boundary conditions and initial conditions

For the membrane,the boundary conditions of its circumferential is fixed in all degree of freedom as well as the side wall.The rigid plate is fixed in all its degree of freedom expect the sliding direction.

A displacement boundary condition is applied to the rigid plate in the sliding direction for a distance equal to 0.027 m,which is sufficient to deliver the volume flow rate necessary to inflate the membrane to the desired height.

When more than one part involved in a simulation,interaction properties need to be defined.In this case,the interaction property has been defined as frictionless tangential behavior.This property has been applied to all surfaces on the model.

8 Numerical Results and Observations

A dynamic explicit step with a total duration time equal to 0.6 seconds is trigged to simulate the inflation process.Fig.9 shows the initial air particles distribution after the element conversion process at the beginning of the simulation.

Figure 9:Initial air particles distribution at t=0 sec.

Fig.10 and Fig.11 shows the membrane inflation at 0.3 seconds and at the end of simulation （t=0.6 seconds）respectively.

Figure 10:Fluid material and structure displacement at t=0.3 sec.

Figure 11:Fluid material and structure displacement at t=0.6 sec.

The equation of state （EOS）used to define the air material behavior is Us-Up with the parameter shown in Table 1.As shown in Fig.12,the numerical results obtained using higher number of elements are closer to the experimental data than the numerical results obtained with lower number of elements.

Figure 12:Bubble height time evolution with different mesh resolution comparing with experimental data.

Figure 13:Equivalent pressure stress for a sample of elements represent the air.

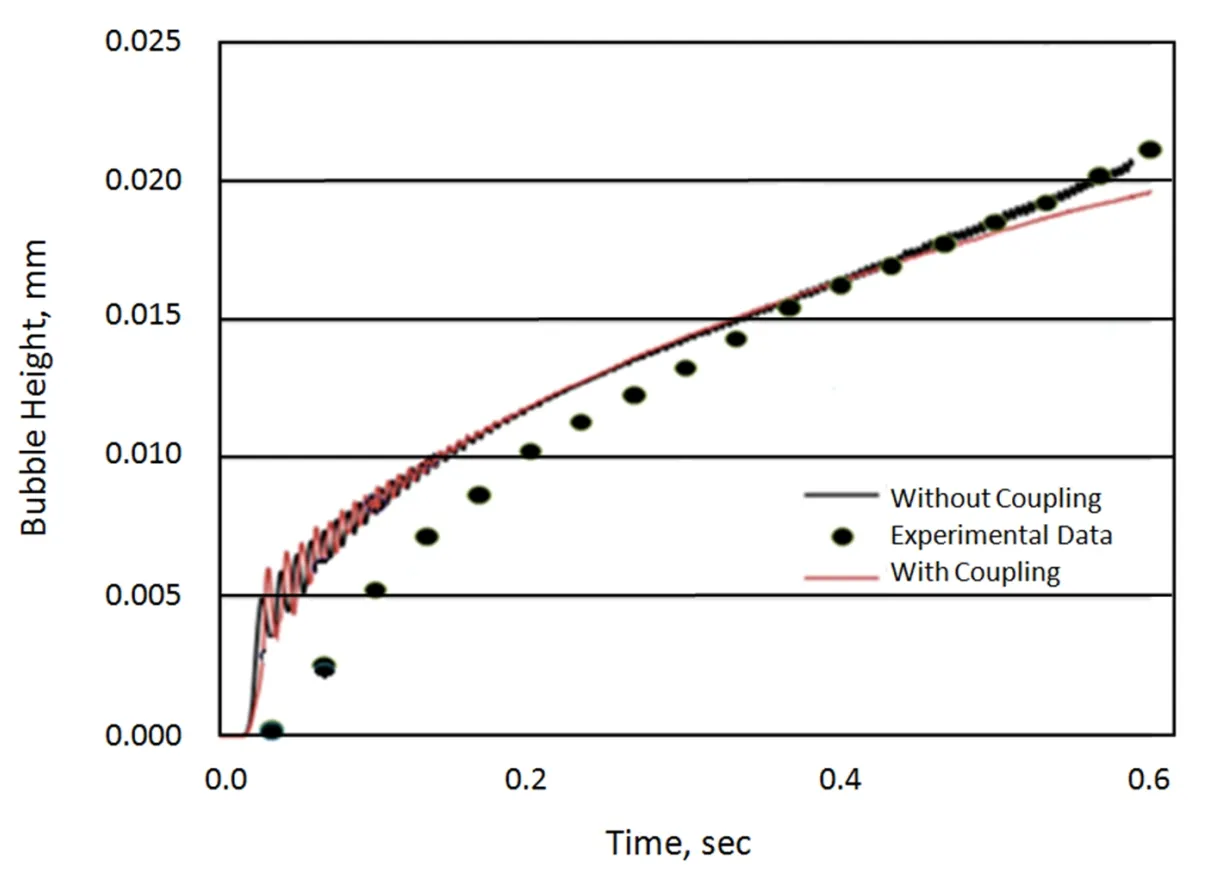
Figure 14:Bubble height time evolution for C01=115590 Pa obtained with ALE method.

In the case of SPH method the pressure of the fluid is represented by the equivalent pressure on the particles.Fig.13 shows the equivalent pressure curves for a sample of particles represent the air fluid.Good Correlation has been obtained between experimental and numerical displacement of the center of the structure as shown in Fig.14.Consequently,the trend of all curves are relatively coincident with experimental pressure data.

9 Conclusions

The paper presents the ALE and SPH methods as well as their limitations for specific problems lime airbag inflation and membrane deployment.Mine explosion,underwater explosion,and bird impact on structures are commonly solved using ALE formulation,in defense industry;some of these problems are solved using SPH method.For the last decade,SPH methods are gaining in accuracy numerical stability,and the use of SPH method is becoming more common in industry for solving fluid structure coupling problems.For instance,in aerospace,where bird impacts on aircraft are very common and cause significant safety threats to commercial and military aircraft.According to FAA （Federal American Aviation）regulations,aircraft should be able to land safely.These applications require a large ALE domain for the coupling between the bird material and the surrounding structure,mainly when the bird is spread all over the space.According to technical reports from engineers in aerospace,ALE formulation is more CPU time consuming and requires more memory allocation that SPH method.In this paper,first,we describe both ALE and SPH methods,and we compare numerical results between the two methods using similar mesh size,each ALE element is replaced by an SPH particle at the element center.Using a simple fluid structure interaction problem,it has been observed that using same mesh size for methods,numerical results,displacement and gas pressure using SPH method,provide good correlation with experimental data.For this particular application,without refining the SPH particles,using same number and elements for SPH and ALE,results from SPH method are in good correlation with those from ALE simulation;in terms of displacement,velocity and Von Mises stress on the structure.Since the ultimate objective is the design of structure resisting to load blast,numerical simulations from ALE and SPH methods can be included in shape design optimization with shape optimal design techniques,see Souli and Zolesio （1993）,and material optimization,see Erchiqui,Souli,and Ben Yedder（2007）.Once simulations are validated by test results,they can be used as design tool for the improvement of the system structure being involved.

Acknowledgement:This project was supported by King Saud University,Deanship of Scientific Research,College of Engineering Research Center.

Aquelet,N.;Souli,M.;Olovson,L.（2005）:Euler Lagrange coupling with damping effects:Application to slamming problems.Computer Methods in Applied Mechanics and Engineering,vol.195,pp.110-132.

Atluri,S.N.;Han,Z.D.;Rajendran,A.M.（2004）:A New Implementation of the Meshless Finite Volume Method,through the MLPG ‘Mixed Approach’.CMES:Computer Modeling in Engineering&Sciences,vol.6,no.6,pp.491-513.

Belytschko,T.;Neal,M.O.（1989）:Contact-impact by the pinball algorithm with penalty,projection,and Lagrangian methods.Proceedings of the symposium on computational techniques for impact,penetration,and perforation of solids AMD,vol.103,New York,NY:ASME,pp.97-140.

Benson,D.J.（1992）:Computational Methods in Lagrangian and Eulerian Hydrocodes.Computer Methods in Applied Mech.and Eng.,vol.99,pp.235-394.

Boyer,D.W.（1960）:An experimental study of the explosion generated by a pressurized sphere.Journal of Fluid Mechanics,vol.9,pp.401-429.

Colagrossi,A.;Landrini,M.（2003）:Numerical simulation of interfacial flows by smoothed particle hydrodynamics.Journal of Computational Physics,pp.191-448.

Doring,M.（2006）:Développement d’une méthode SPH pour les applications à surface libre en hydrodynamique,PhD thesis,Ecole Centrale de Nantes,France.

Erchiqui,F.;Derdouri,A.;Gakwaya,A.;Verron,E.（2001）:Free inflation of flat thermoplastic membrane:numerical analysis and experimental validation.Entropie,No.235/236,pp.118-125.

Erchiqui,F.;Souli,M.;Ben Yedder,R.（2007）:Nonisothermal finite-element analysis of thermoforming of polyethylene terephthalate sheet:Incomplete effect of the forming stage.Polymer Engineering and Science,vol.47,no.12,pp.2129-2144.

Gingold,R.A.;Monaghan,J.J.（1977）:Smoothed particle hydrodynamics:theory and applications to non-spherical stars.Monthly Notices of the Royal Astronomical Society,vol.181,pp.375-389.

Hallquist,J.O.（1998）:LS-DYNA theory manual.Livermore Software Technology Corporation.

Han,Z.D.;Atluri,S.N.（2014）:On the Meshless Local Petrov-Galerkin MLPGEshelby Method in Computational,Finite Deformation Solid Mechanics-Part II.CMES:Computer Modeling in Engineering&Sciences,vol.97,no.3,pp.199-237.

Lanson,N.（2003）:Etude des méthodes particulaires renormalisées.Applications aux problèmes de dynamique rapide,PhD thesis,Université Toulouse 3 INSA.

Libersky,L.D.;Petschek,A.G.;Carney,T.C.;Hipp,J.R.;Allahdadi,F.A.（1993）:High strain Lagrangian hydrodynamics:a three-dimensional SPH code for dynamic material response.Journal of Computational Physics,vol.109,pp.67-75.

Liu,M.B.;Liu,G.R.（2010）:Smoothed Particle Hydrodynamics （SPH）:an overview and recent developments.Arch Computer Methods Eng.,vol.17,pp.25–76.

Longatte,E.;Bendjeddou,Z.;Souli,M.（2003）:Application of Arbitrary Lagrange Euler Formulations to Flow-Induced Vibration problems.Journal of Pressure Vessel and Technology,vol.125,no.4,pp.411-417.

Longatte,E.;Verreman,V.;Souli,M.（2009）:Time marching for simulation of Fluid-Structure Interaction Problems.Journal of Fluids and Structures,vol.25,no.1,pp.95-111.

Lucy,L.B.（1977）:A numerical approach to the testing of fission hypothesis.As-tronom.J.,vol.82,pp.1013-1024.

Monaghan,J.J.;Gingold,R.A.（1983）:Shock Simulation by particle method SPH.Journal of Computational Physics,vol.52,pp.374-389.

Narsh,S.P.（1980）:LASL Shock Hugoniot Data,University of California Press 1980.

Oger,G.（2006）:Aspects theoriques de la m’ethode SPH et applications a l’hydrodynamique a surface,PhD Thesis,Ecole Centrale de Nantes.

Ozdemir,Z.;Souli,M.;Fahjan,Y.M.（2010）:Application of nonlinear fluidstructure interaction methods to seismic analysis of anchored and unanchored tanks.Engineering Structures,vol.32,no.2,pp.409-423.

Randles,P.W.;Libersky,L.D.（1996）:Smoothed Particle Hydrodynamics:some recent improvements and applications.Computer Methods Appl.Mech.Eng.,vol.139,pp.375-408.

Shuyao,L.;Atluri,S.N.（2002）:A Meshless Local Petrov-Galerkin Method for Solving the Bending Problem of a Thin Plate.CMES:Computer Modeling in Engineering&Sciences,vol.3,no.1,pp.53-63.

Souli,M.;Zolesio,J.P.（1993）:Shape derivative of discretized problems.Computer Methods in Applied Mechanics and Engineering,vol.108,pp.187-199.

Vignjevic,R.;Campbell,J.;Libersky,L.D.（2000）:A treatment of zero-energy modes in the smoothed particle hydrodynamics method.Compute.Methods Appl.Mech.Eng.,vol.184,pp.67–85.

Vila,J.（1999）:On particle weighted method and smoothed particle hydrodynamics.Mathematical Models and Method in Applied Science,vol.9,pp.161-209.

Vila,J.（2005）:SPH renormalized hybrid methods for conservation laws:applications to free surface flows,Mesh free Methods for Partial Differential Equations II,vol.43 of Lecture Notes in Computational Science and Engineering,Springer.

Von Neumann,J.;Richtmeyer,R.D.（1950）:A method for the numerical calculation of hydrodynamical shocks.Journal of Applied Physics,vol.21,pp.232.

Zaoui,A.;Madouri,D.;Ferhat,M.（2009）:First-principles study of the ground state stability of III-V bismuth compounds,Philosophical Magazine Letters.

1Mechanical Engineering Department,King Saud University,Saudi Arabia.

2Corresponding author.Tel.:+966 11 467 6675;fax:+966 11 467 6652;E-mail:ebahkali@ksu.edu.sa

3Universite de Lille1,LML UMR CNRS 8107,France.