多险种复合广义齐次Poisson过程的破产概率
2015-12-13杨忻怡王志福张拓
杨忻怡 王志福 张拓
(渤海大学数理学院,辽宁锦州 121013)
多险种复合广义齐次Poisson过程的破产概率
杨忻怡 王志福 张拓
(渤海大学数理学院,辽宁锦州 121013)
破产概率的计算是精算破产理论的经典问题,对当前保险经营风险的度量有重要的理论意义和参考价值。由于保险公司规模的不断扩大,用单一的风险模型来描述风险过程存在局限性。本文建立了复合广义齐次Possion过程的风险模型,并对其索赔过程的性质进行了研究,讨论了此模型的破产概率从而求出Lundberg上界和破产概率的一般表达式。
多险种风险模型 破产概率 Poisson过程
在保险风险理论中,经典模型[1]可由下式表示出来:


1 多险种的风险模型


引理1 复合广义poisson模型可转换为经典复合poisson模型,即有

其中
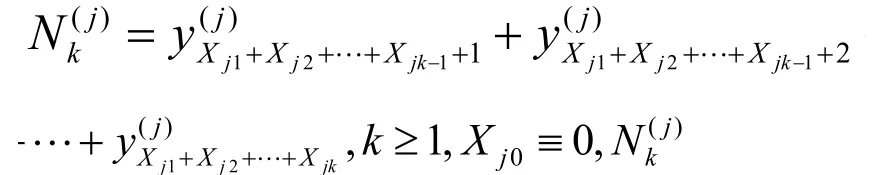
由引理1,所建模型(1)式可以改写为
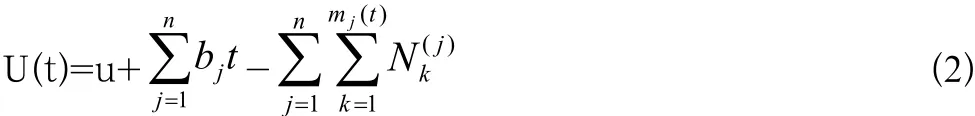
为研究破产概率,作以下假设:

定义1:
2 破产概率的估计
定理1:对于风险过程﹛s( t),t ≥0﹜,存在函数
证明 因为


定理自然成立。
定理2:方程 g (r )=0存在唯一正解R,R为调节系数
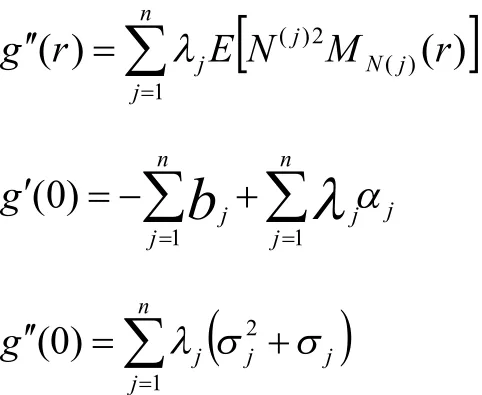
又 g (r )=0, g(+∞)=+∞,所以 g (r)为凸函数,从而 g(r )=0方程至多有两个解。显然 r=0是平凡解,所以方程 g (r )=0有唯一正解,记为R。


证明: 对于任意 0 ≤s≤t,有

证毕。

证明: 记 Mu(t)= e-RU(t),对于任意时刻 t< T,则 t∧ T是﹛Ft,t≥0﹜的停时,根据鞅的停时定理[4],有

以I( A)表示集合A的示性函数有

结合(4)得到

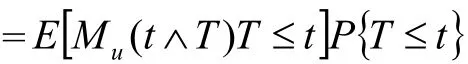
当 +∞→t 时得
证毕。
[1]陈世学.严颖 译.GERBER H U.数学风险论导引[M].北京:世界图书出版公司北京公司,1997;129-171.
[2]EMBRECHTS P.KLUPPELBERG C.MIKOSCHT.Modelling Extremal Events for Insurance and Finance[M].Berlin: Springer Verlag, 1997: 28-34.
[3]LI Ze-hui ZHU Jin-xia,CHEN Feng.Study of a risk model based on the entrance process [J].Statistics and Probability Letters,2005,72;1-10.
[4]何声武,谢盛荣,程依明译.ROSS S M.随机过程[M].北京:中国统计出版社,1997:265-270.
杨忻怡(1990—),女,辽宁铁岭人,渤海大学数理学院硕士研究生,研究方向:应用数学(概率论与数理统计)。
